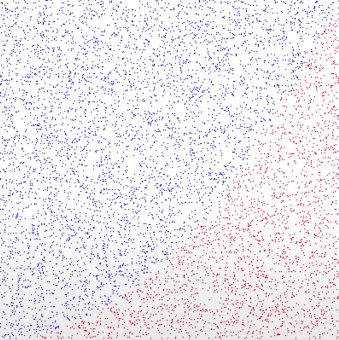
Example 1: computing PI

• Random sample points in [-1,1] x [-1,1]
• Count how many points are within the circle
• Pi = # of points in the circle / # of pints * baseArea ( 4 )

Example 2: computing Integral

• Random sample point in [0,1] x [0,1]
• Compute probability that x^2<=y

Monte Carlo Methods

• Solving the reinforcement learning problem
• Based on averaging sample returns
• Use: broadly for estimation method whose operation involves a significant random component
• 2 methods:
  • First-visit MC method estimates vπ(s) as the average of the returns following first visits to s
  • Every-visit MC method averages the returns following all visits to s

Converge

• First-visit MC
  • Easy
  • The standard deviation of its error falls as 1/ ( n^0.5), where n is the number of returns averaged.
• Every-visit MC
  • Less straightforward
  • Converge asymptotically to vπ(s) (Singh and Sutton, 1996)

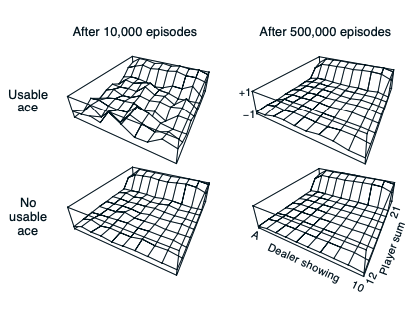
Example 5.1: Blackjack

• Obtain cards the sum of whose numerical values is as great as possible without exceeding 21
• y = arg max f(t), y <= 21
• If the dealer goes bust, then the player wins; otherwise, the outcome—win, lose, or draw—is determined by whose final sum is closer to 21.
•  In any event, after 500,000 games the value function is very well approximated.

Blackjack rules

• Rewards of +1, −1, and 0 are given for winning, losing, and drawing
• All rewards within a game are zero, and we do not discount (γ = 1)
• The player’s actions are to hit or to stick
• The player makes decisions on the basis of three variables:
  1. his current sum (12–21)
  2. the dealer’s one showing card (ace–10)
  3. whether or not he holds a usable ace
• This makes for a total of 200 states.
• Note that in this task the same state never recurs within one episode, so there is no difference between first-visit and every-visit MC methods.

Why not DP

• DP methods require the distribution of next events—in particular, they require the quantities p(s 0 , r|s, a)—and it is not easy to determine these for blackjack
• Expected rewards and transition probabilities ( often complex and error-prone ) must be computed before DP can be applied
• In contrast, generating the sample games required by Monte Carlo methods is easy
• The ability of Monte Carlo methods to work with sample episodes alone can be a significant advantage even when one has complete knowledge of the environment’s dynamics.

Fundamental differences

• Sampling
  • DP diagram shows all possible transitions
  • Monte Carlo diagram shows only those sampled on the one episode
• Tracing
  • DP diagram includes only one-step transitions
  • Monte Carlo diagram goes all the way to the end of the episode.

Computational Expense

• Computational expense of estimating the value of a single state is independent of the number of states
• Monte Carlo methods particularly attractive when one requires the value of only one or a subset of states
• One can generate many sample episodes starting from the states of interest, averaging returns from only these states ignoring all others.