FuSeConv: Fully Separable Convolutions for Fast Inference in Systolic Arrays
* Department of Computer Science and Engineering, IIT Madras
# School of Electrical and Computer Engineering, Purdue University
Surya Selvam\( ^{*\#} \), Vinod Ganesan \( ^* \) and Pratyush Kumar\( ^* \)


Efficient DNN Inference on Hardware is still a challenge
- DNNs achieve SOTA on various tasks
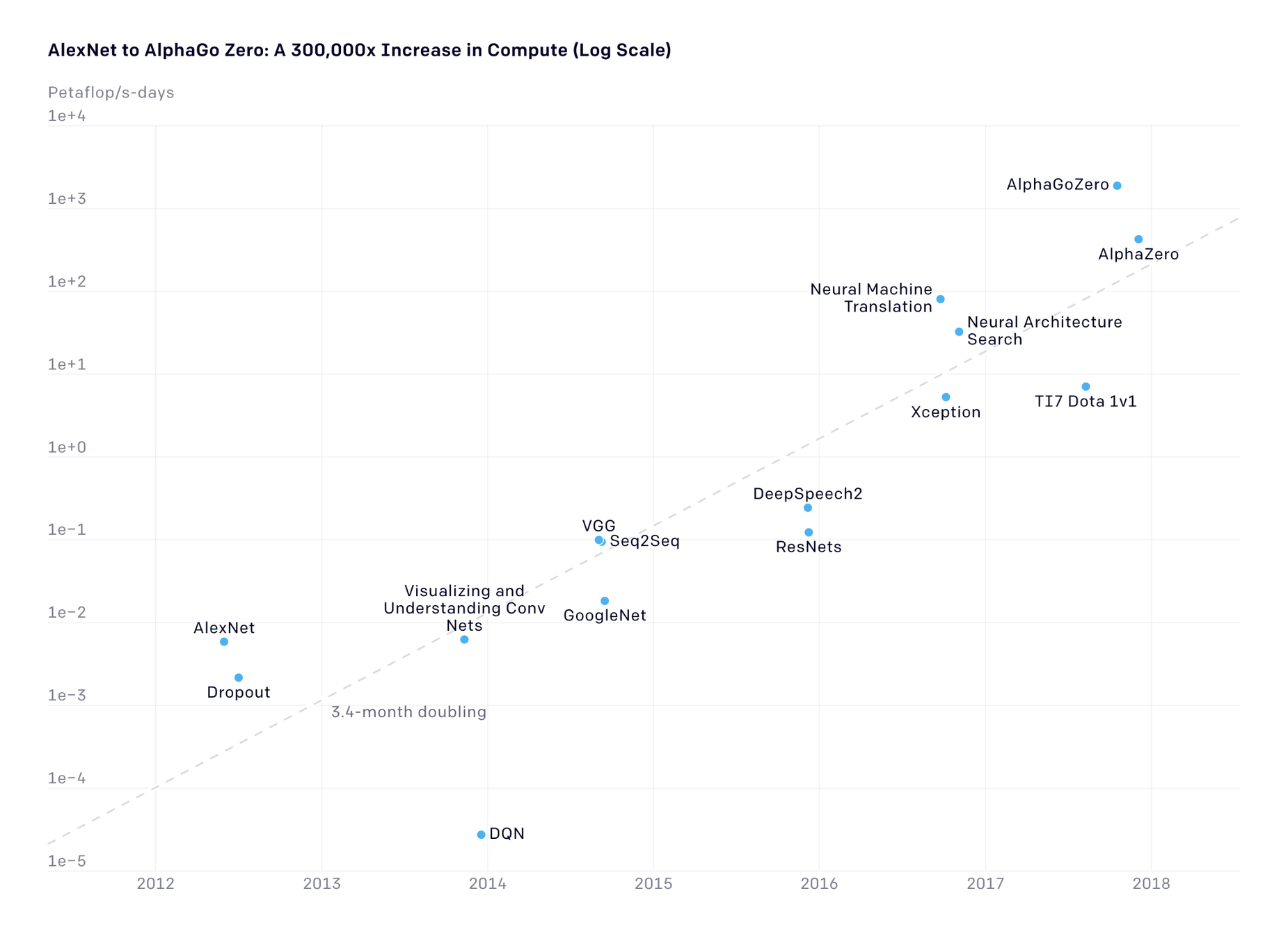
10x/year
Source: OpenAI Blog
Moore's law
There is a huge demand gap
Solution
Domain-Specific Accelerators and Efficient DNN operators
Efficient Inference: Solutions

Systolic Arrays in TPUs
25-29x more performant than GPUs
Domain-Specific Hardware Accelerators
Efficient DNN Operator
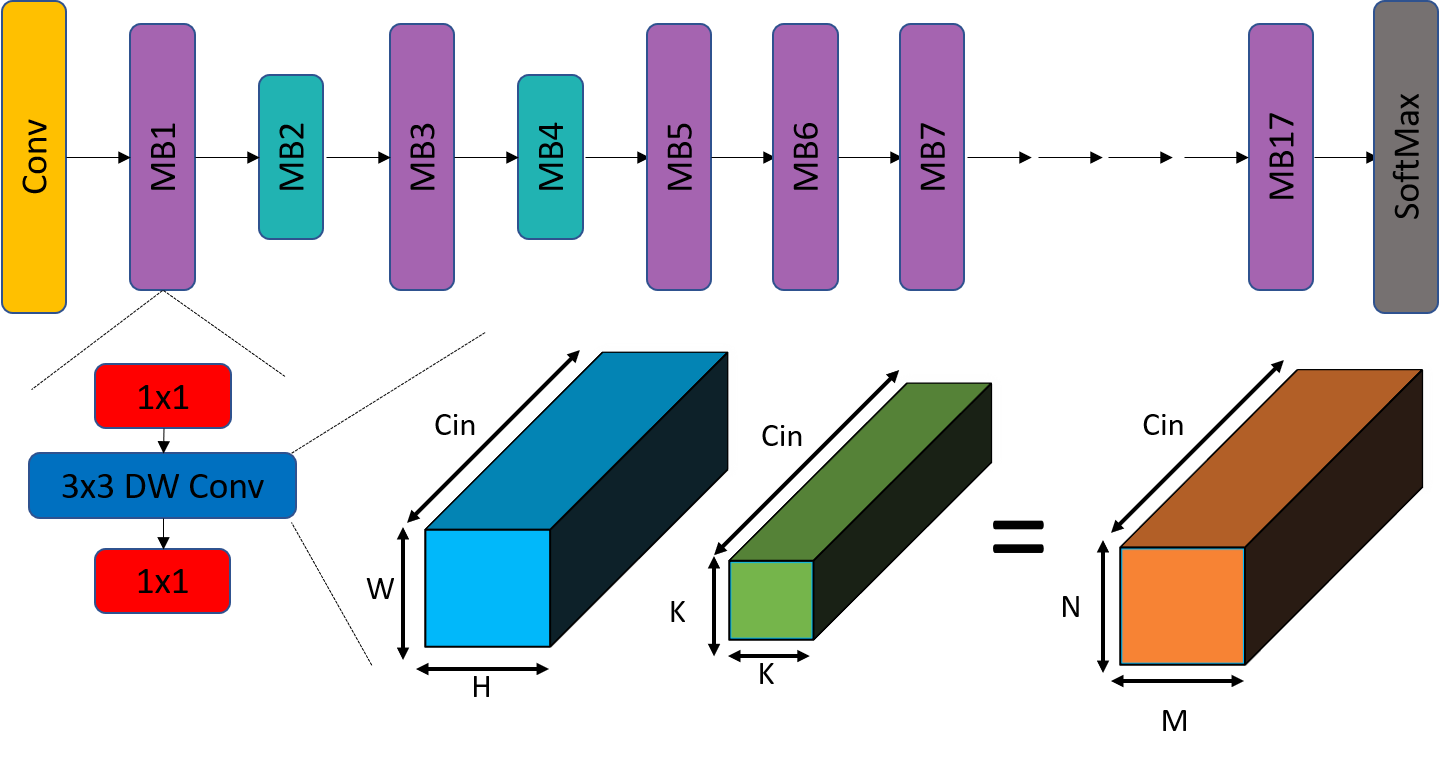
Depthwise Separable Convolutions
Computationally Efficient and ubiquitous
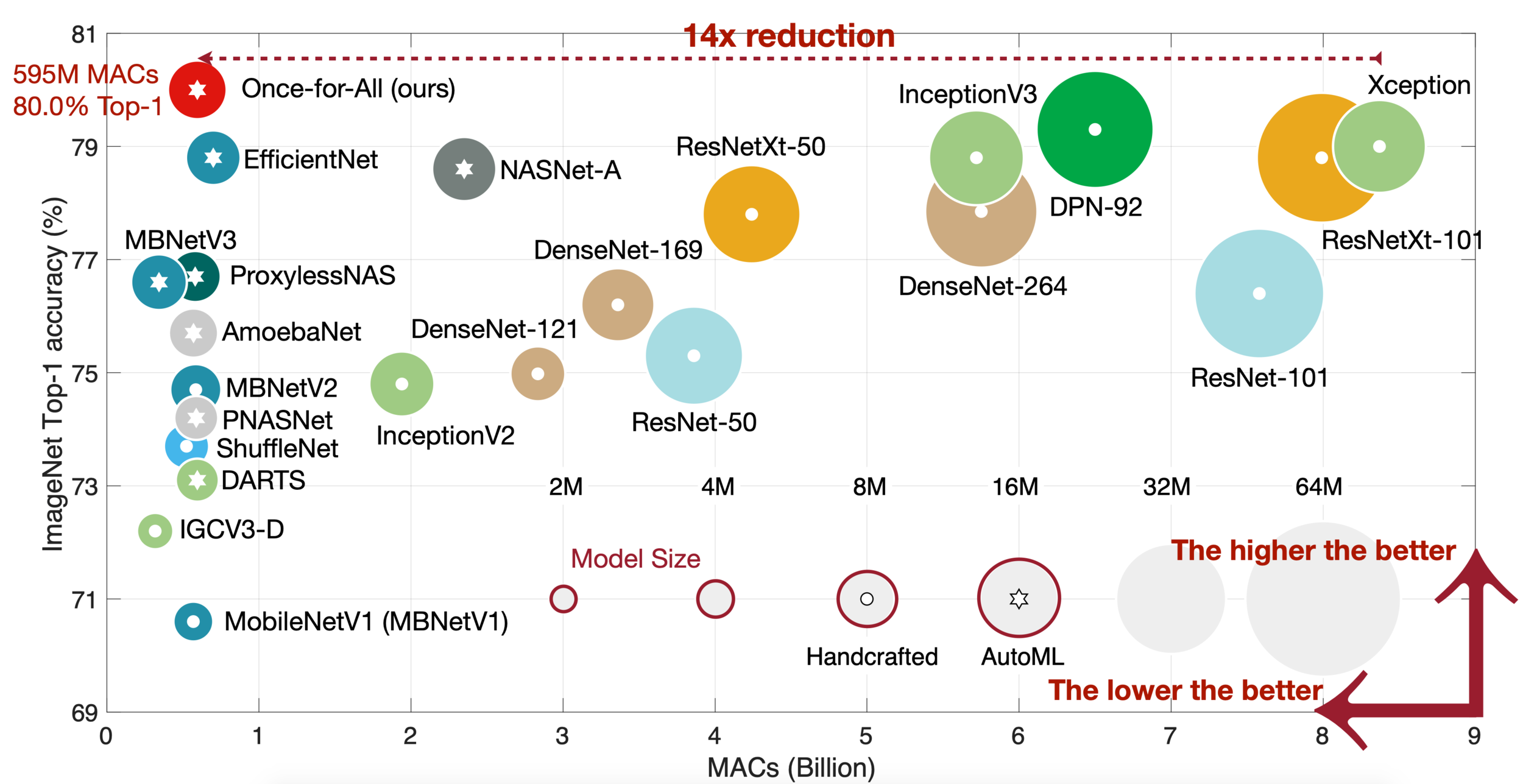
Source: Once For All
Surprisingly, the composition of efficient solutions is inefficient
Comparing MobileNet-V2 with ResNet-50
> Why are depthwise convolutions inefficient on systolic arrays?
> What can we do to make DW convolution faster on systolic arrays?
> How good is the inference performance of our proposed solution?
Incommensurate
Scaling
In this work
> Why are depthwise convolutions inefficient on systolic arrays?
Formal analysis using Systolic-Algorithms
FuSeConv: Fully Separable 1D Convolutions, our hardware/software co-design solution
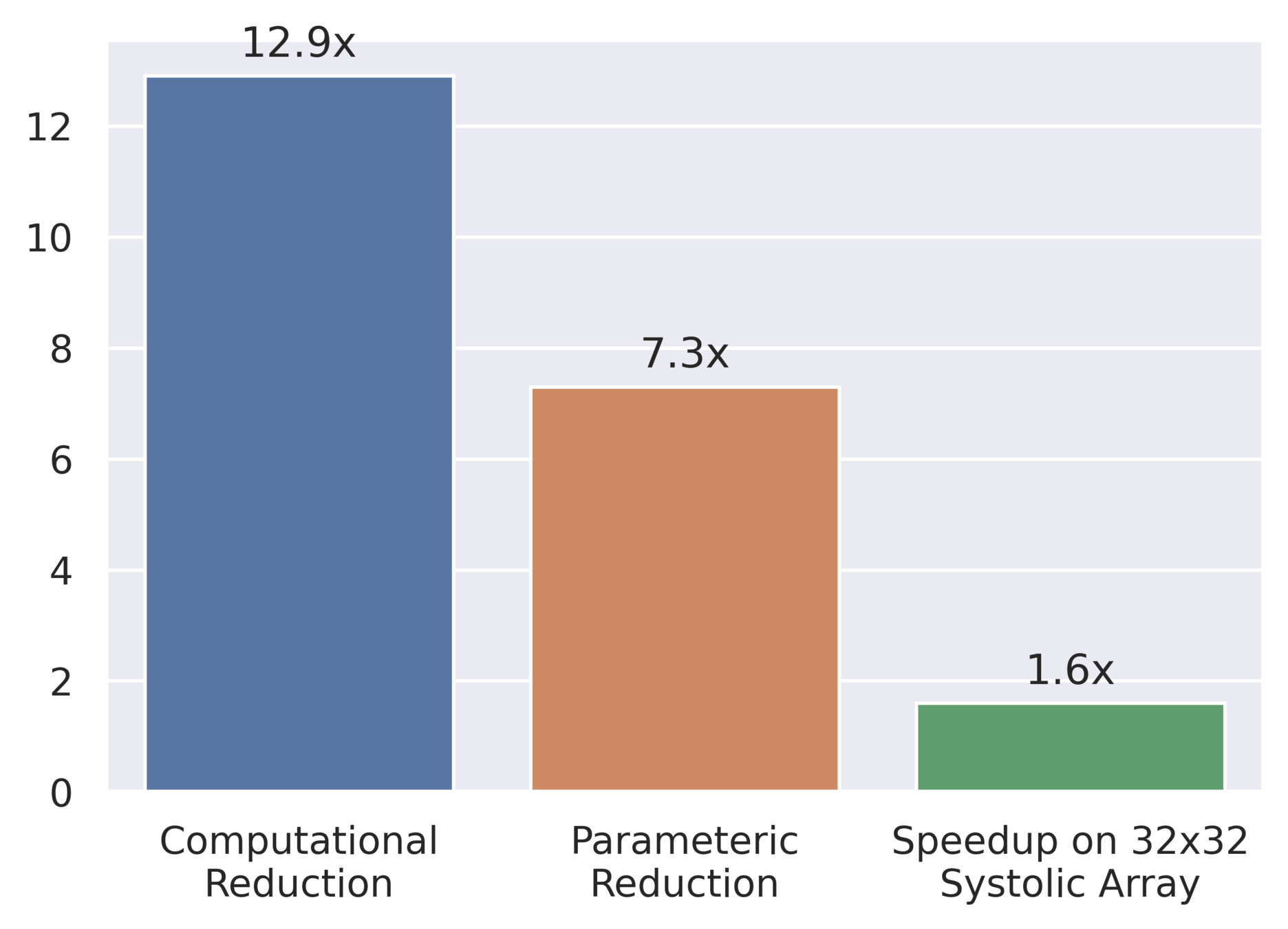
FuSeConv is 3x-7x more faster on 64x64 Systolic Arrays with minimum overhead
> What can we do to make DW convolution faster on systolic arrays?
> How good is the inference performance of our proposed solution?
Terminologies Recap
Standard Convolution
Depthwise Separable Convolution = Depthwise Conv + Pointwise Conv


FLOPS = N x M x K x K x C\( _{in}\) x C\( _{out}\)
FLOPS = N x M x C\( _{in}\) x K x K + N x M x C\( _{in}\) x C\( _{out}\)
Systolic Algorithms
> A class of algorithms that runs efficiently on systolic architectures
> Computational loops are transformed into Regular Iterative Algorithm (RIA)
> RIAs that have constant offsets only can be synthesized on systolic arrays
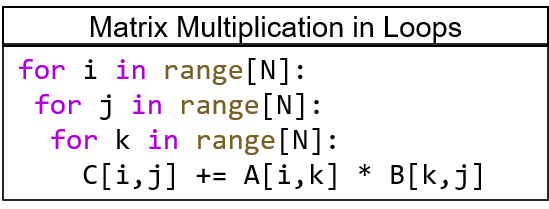

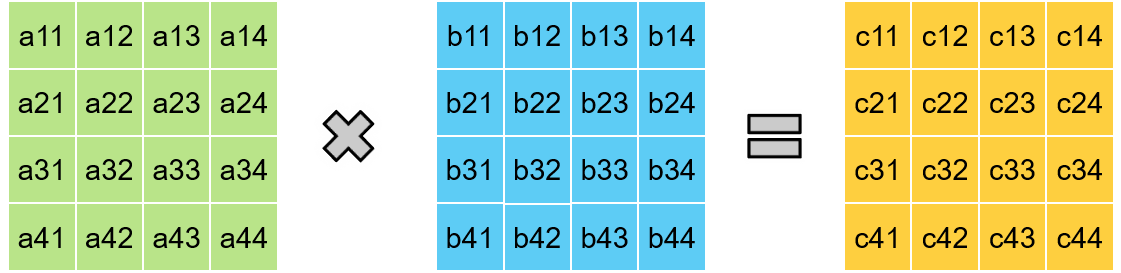

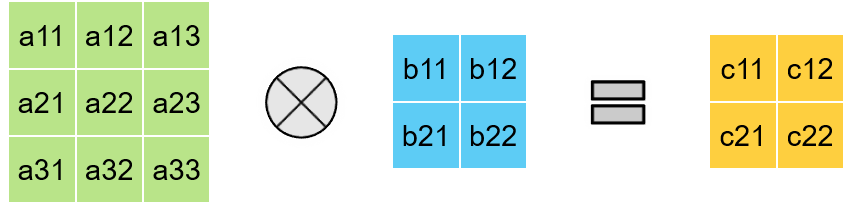
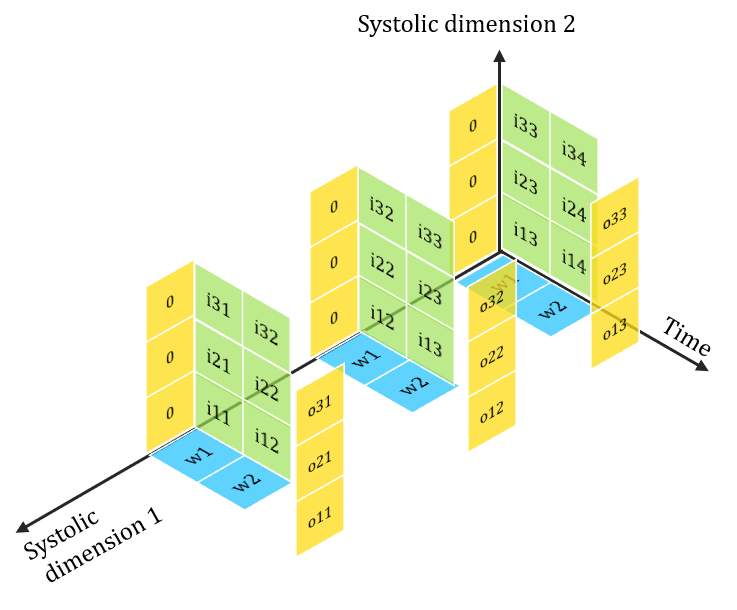
Mapping Systolic Algorithms to Systolic Arrays
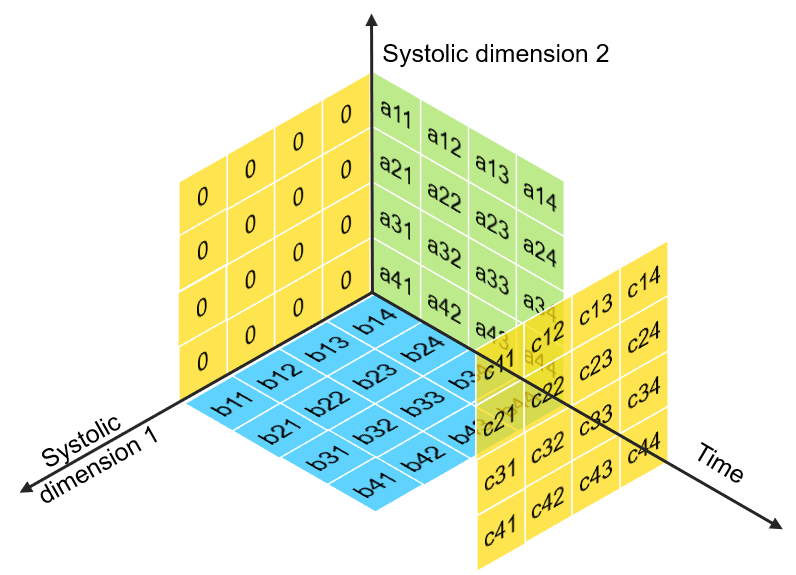


> i, j indices maps to Spatial dimensions of array
> k index maps to Temporal dimension
Time
Dim1
Dim2
What about 2D Convolutions?


> Non-Constant Offset indices in RIA

> 2D Convolution is not a Systolic Algorithm
Then how are 2D Convolutions mapped onto Systolic Arrays?


After im2col transformation
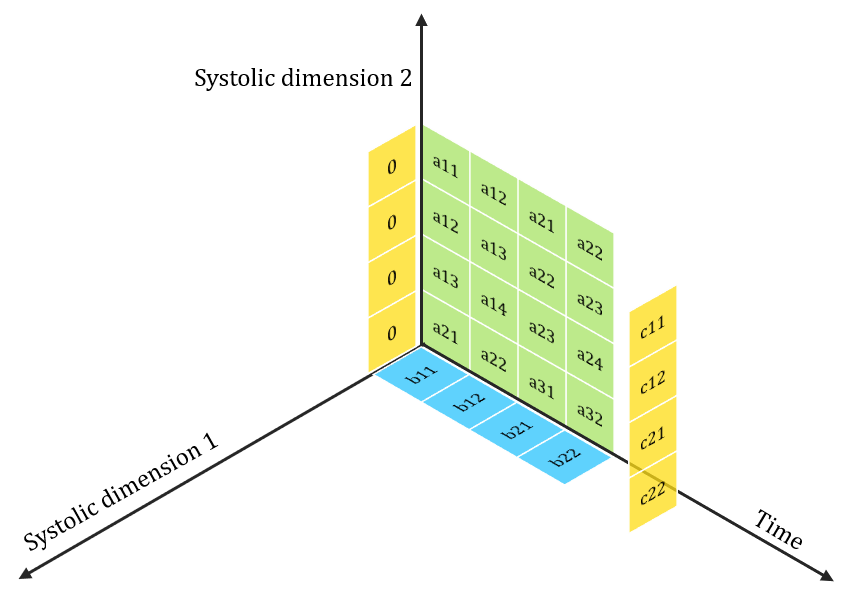
Under Utilization
Then, How to make them efficient on Systolic?
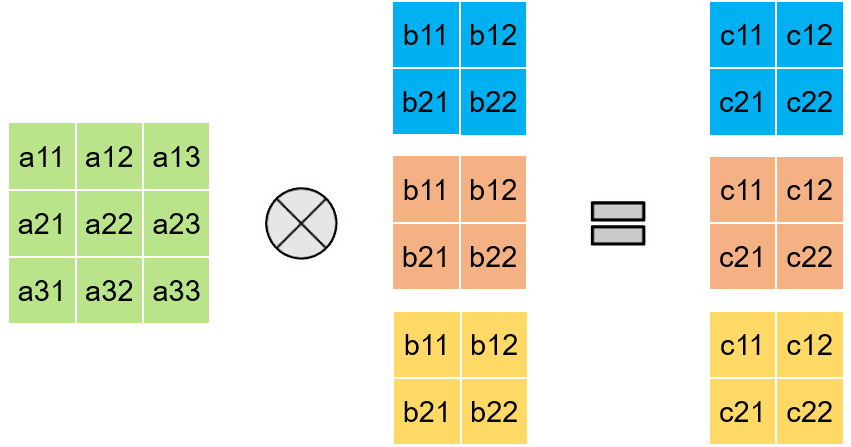
> More filters -> Data reuse -> High Utilization
> Extendable for convolution with channels too
2D Convolution with Multiple Filters
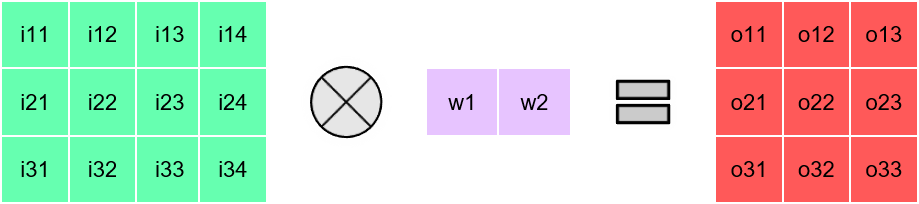
Lets look at Depthwise Convolutions
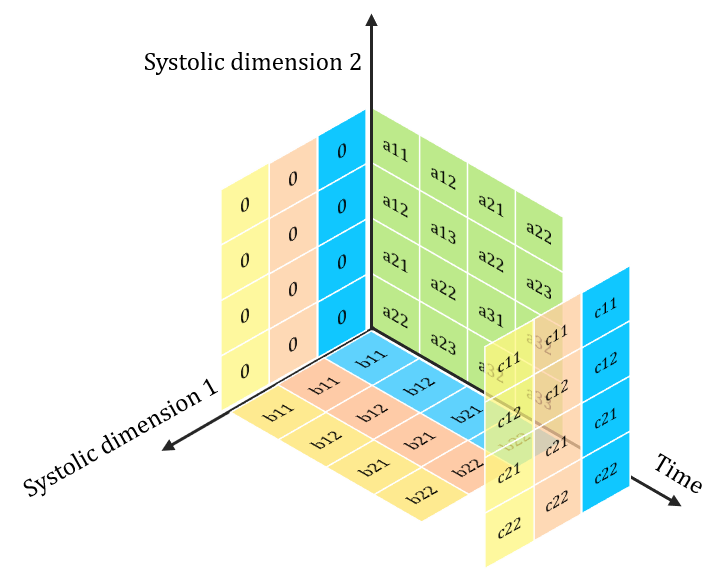
> Equivalent to C\( _{in}\) 2D single channel Convolutions
> No Filter Reuse availble in Depthwise Convolution
Problem: Poor Utilization on Systolic Arrays
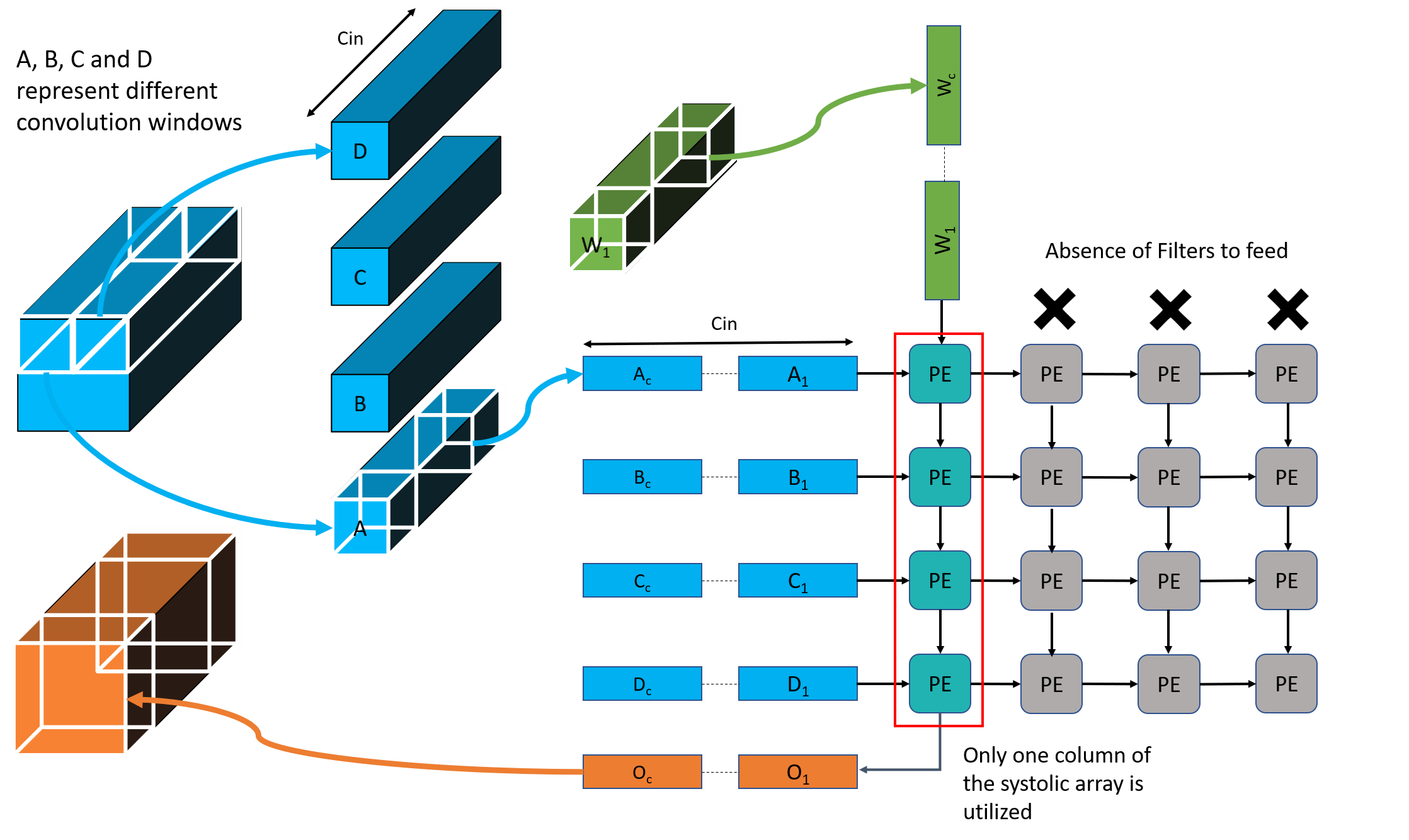
Each channel-wise 2D convolution is sequential!!
FuSeConv: Our HW/SW Co-Design Solution


Fully Separable Convolution (FuSeConv) : Composes of 1D depthwise convolutions and pointwise convolution
Depthwise Separable Convolution
Full Variant (D = 1)
Half Variant (D = 2)
FuSeConv is a systolic algorithm !
> FuSeConv composes of only 1D convolutions.
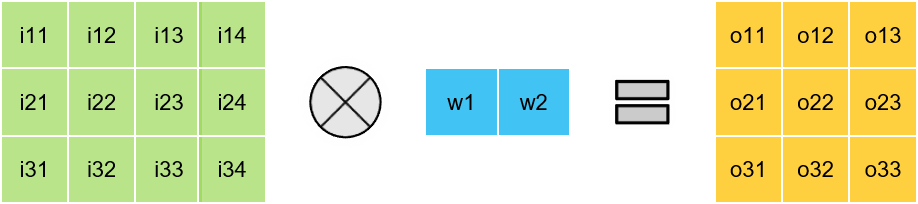
> 1 x K & K x 1depthwise convolutions
> 1 x 1 Pointwise Convolution
Matrix Multiplication
1D Convolutions


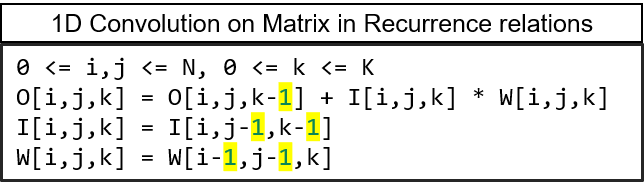
> Constant Offset => Systolic Algorithm
Proposed Hardware Architecture
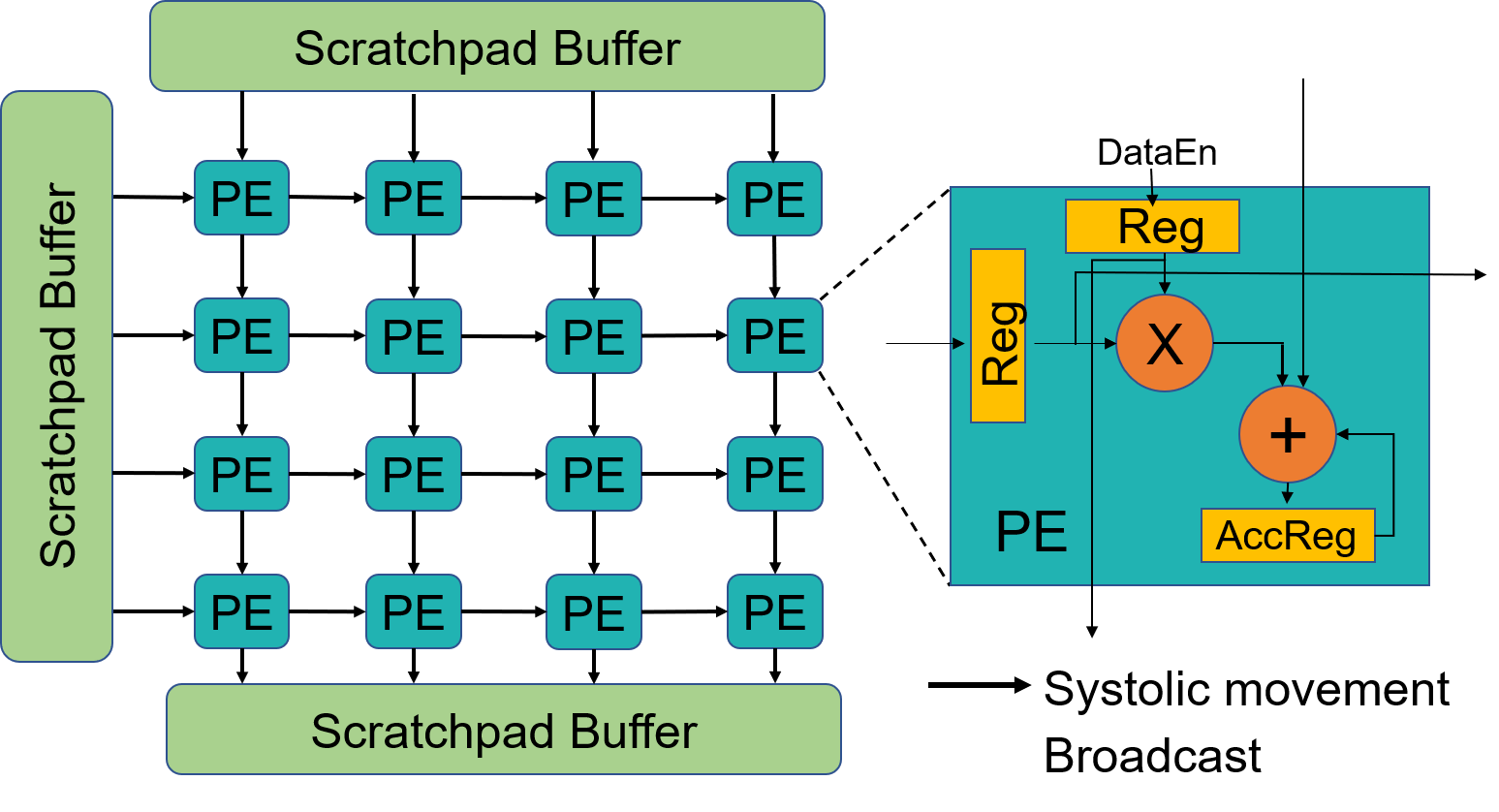
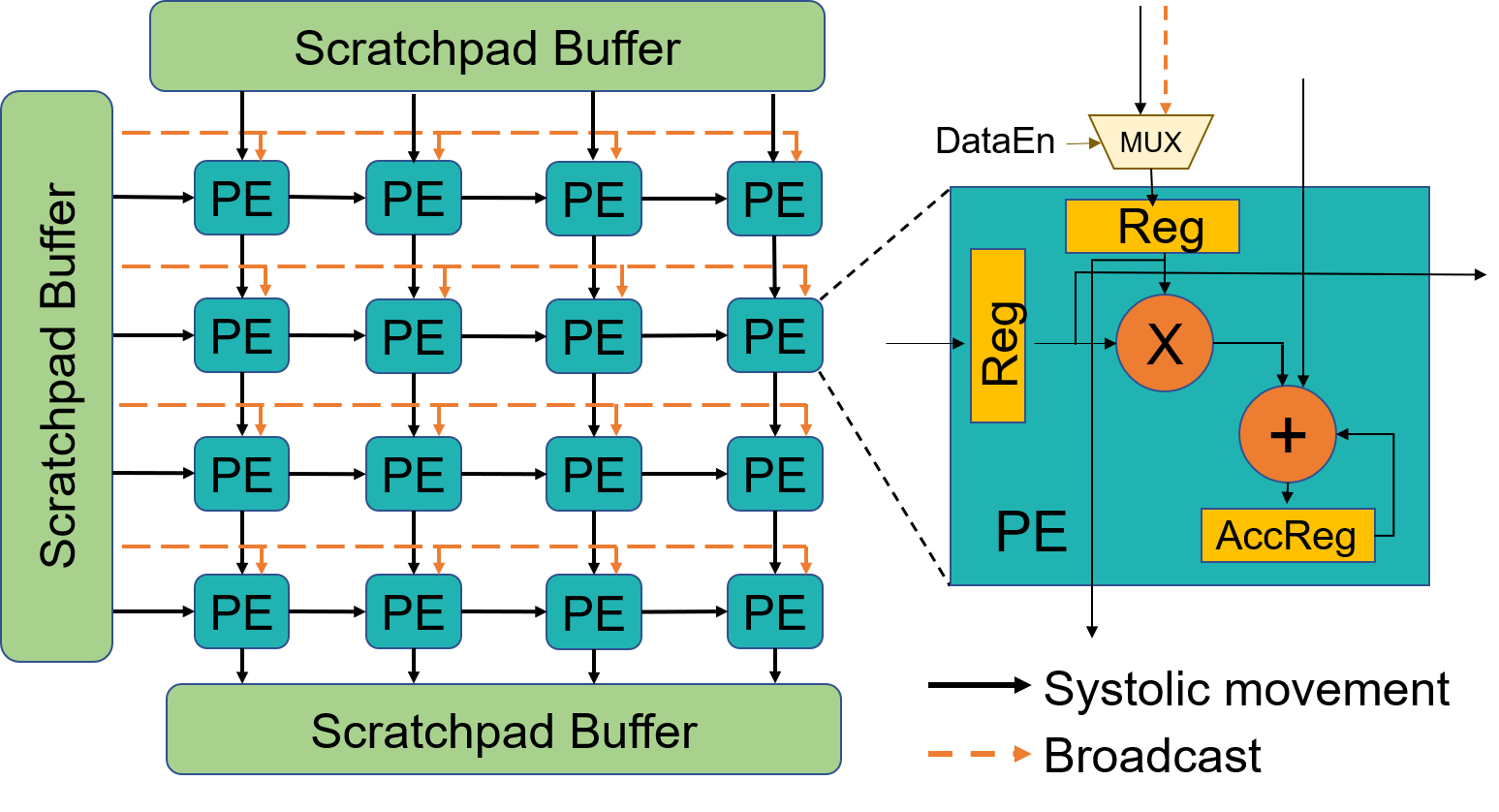
Execute independent 1D convolutions
On 32 x 32 Systolics
| Area | 4.35% |
| Power | 2.25% |
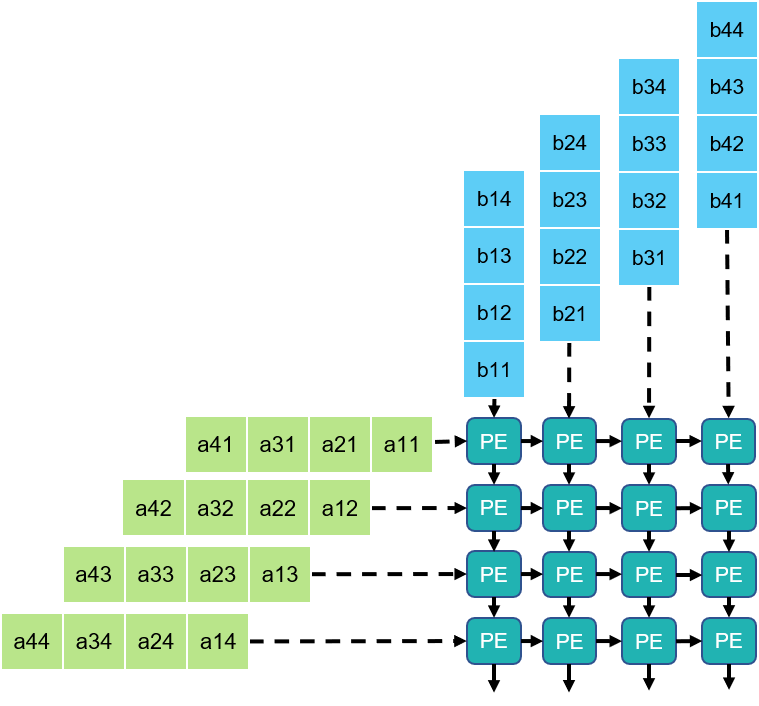
FuSeConv Mapping: Illustration

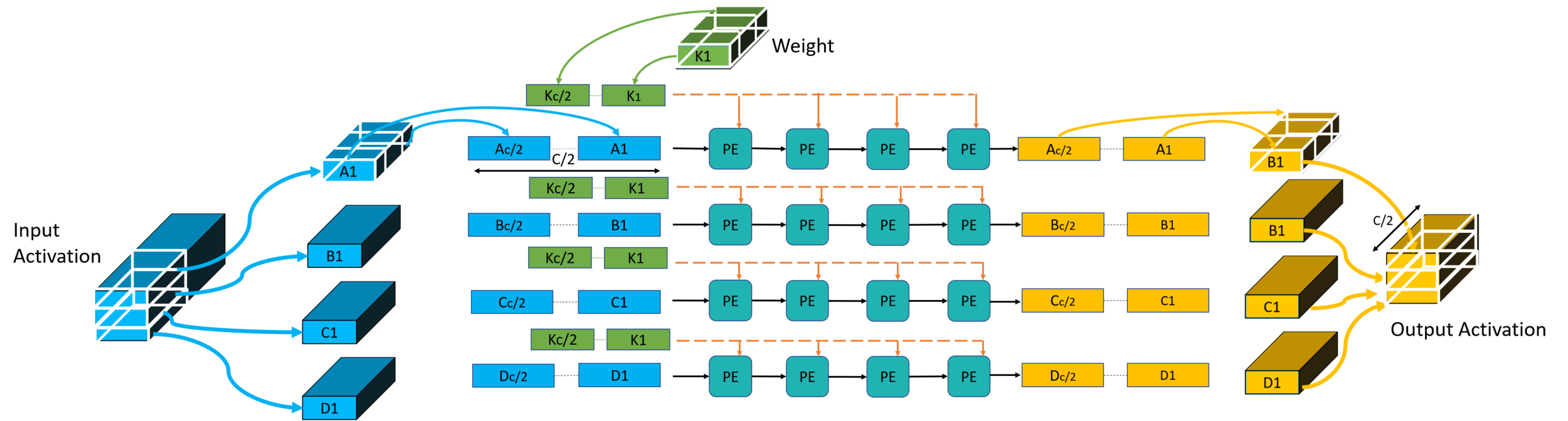
Efficiency of FuSeConv on our Proposed Hardware

Channel 0
Channel 1
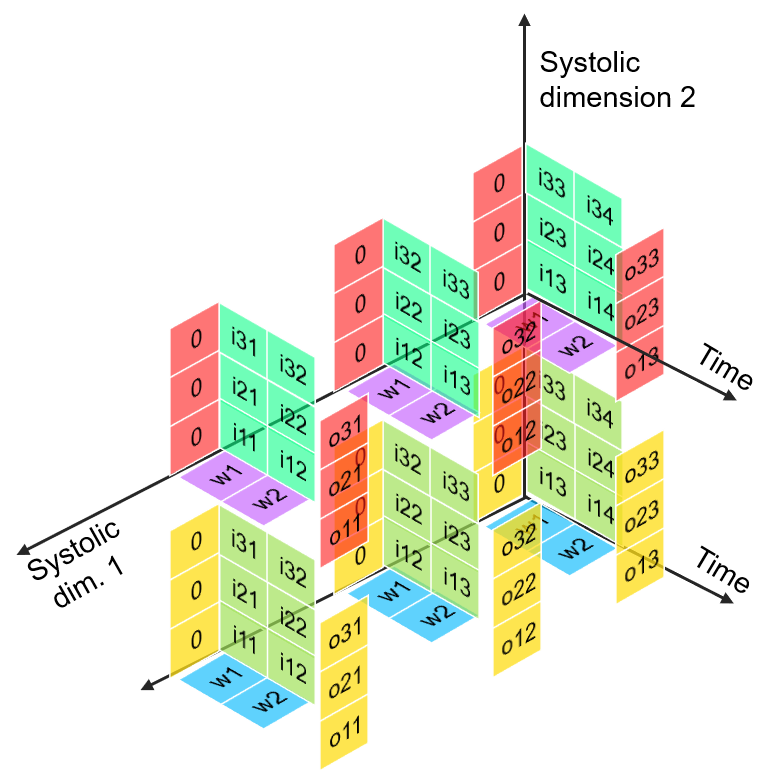
> Channelwise 1D convolutions can be computed in parallel
> FuSeConv + our dataflow mapping exploits parallelism which were absent in depthwise convolutions mapping natively on Systolic Arrays
Multiple Channels can execute in parallel along dimension 2
Evaluation
> Evaluate 4 FuSe variants and compare with baseline
> Analytical latency model based on SCALE-SIM
> MobileNets (V1, V2, V3-Small, V3-Large) and MnasNet-B1
Choose half of layers greedily to maximize speedup of layer
> Full (D = 1) FuSe
> Half (D = 2) FuSe
> 50% Full FuSe
> 50% Half FuSe
> Latency = Load Values + Compute + Communicate PSums + Flush Outputs
All layers are replaced with FuSeConv
Evaluation
| Network | Accuracy | FLOPS (M) | Params (M) | Speedup |
|---|---|---|---|---|
| MobileNet-V2 Baseline | 72 | 315 | 3.5 | 1x |
| MobileNet-V2 Full FuSe | 72.49 | 430 | 4.46 | 5.1x |
| MobileNet-V2 Half FuSe | 70.8 | 300 | 3.46 | 7.23x |
| MobileNet-V2 50% Full FuSe | 72.11 | 361 | 3.61 | 2.0x |
| MobileNet-V2 50% Half FuSe | 71.98 | 305 | 3.49 | 2.1x |
| Network | Accuracy | FLOPS (M) | Params (M) | Speedup |
|---|---|---|---|---|
| MobileNet-V3 Small Baseline | 67.4 | 66 | 2.93 | 1 |
| MobileNet-V3 Small Full FuSe | 67.17 | 84 | 4.44 | 3.02x |
| MobileNet-V3 Small Half FuSe | 64.55 | 61 | 2.89 | 4.16x |
| MobileNet-V3 Small 50% Full FuSe | 67.91 | 73 | 3.18 | 1.6x |
| MobileNet-V3 Small 50% Half FuSe | 66.9 | 63 | 2.92 | 1.68x |
Average drop ~1% in Half Variants, drop ~0.3% in Full Variants
Evaluation
Inference Latency and Speedup on 64 x 64 Systolic Array
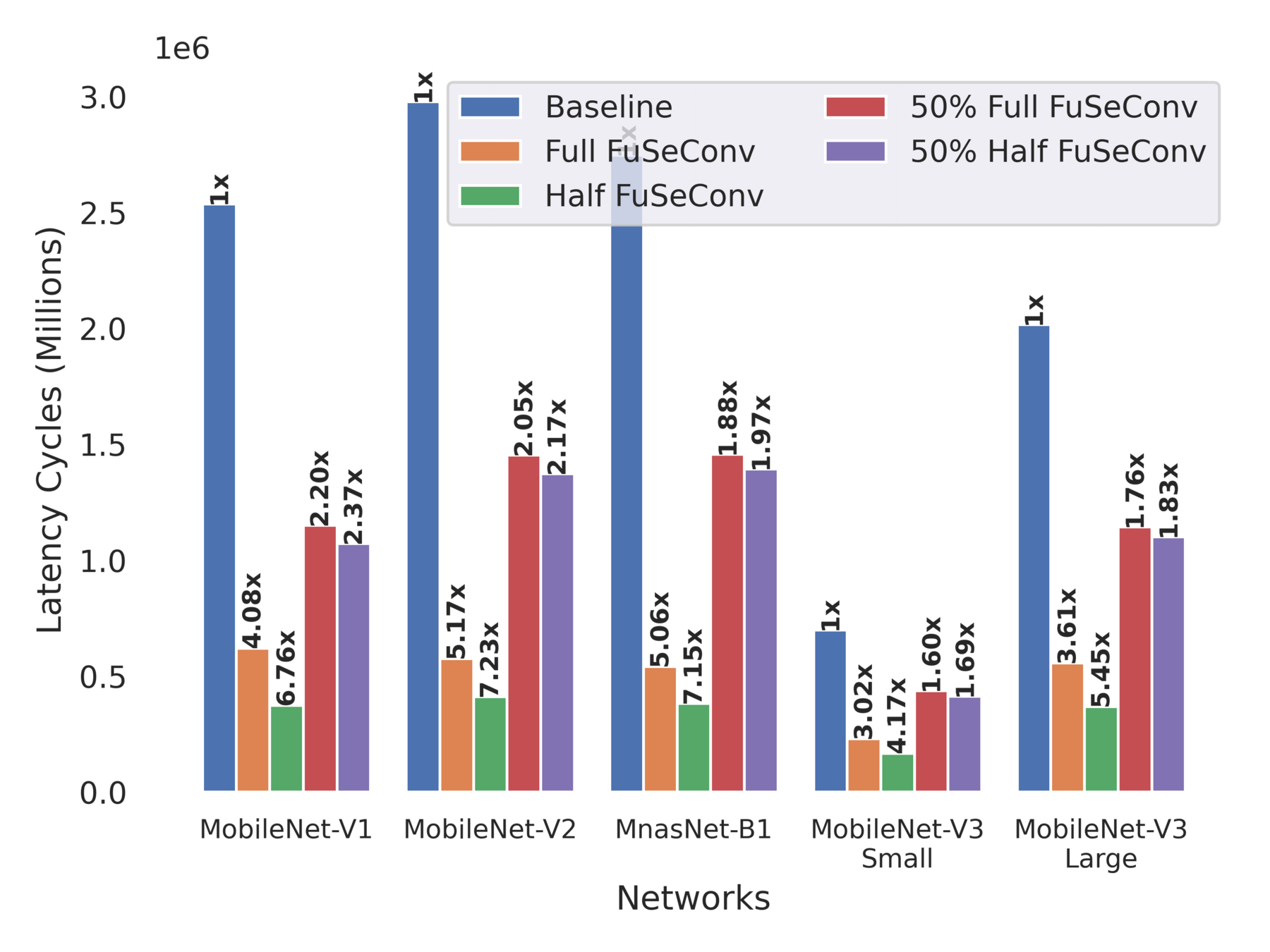
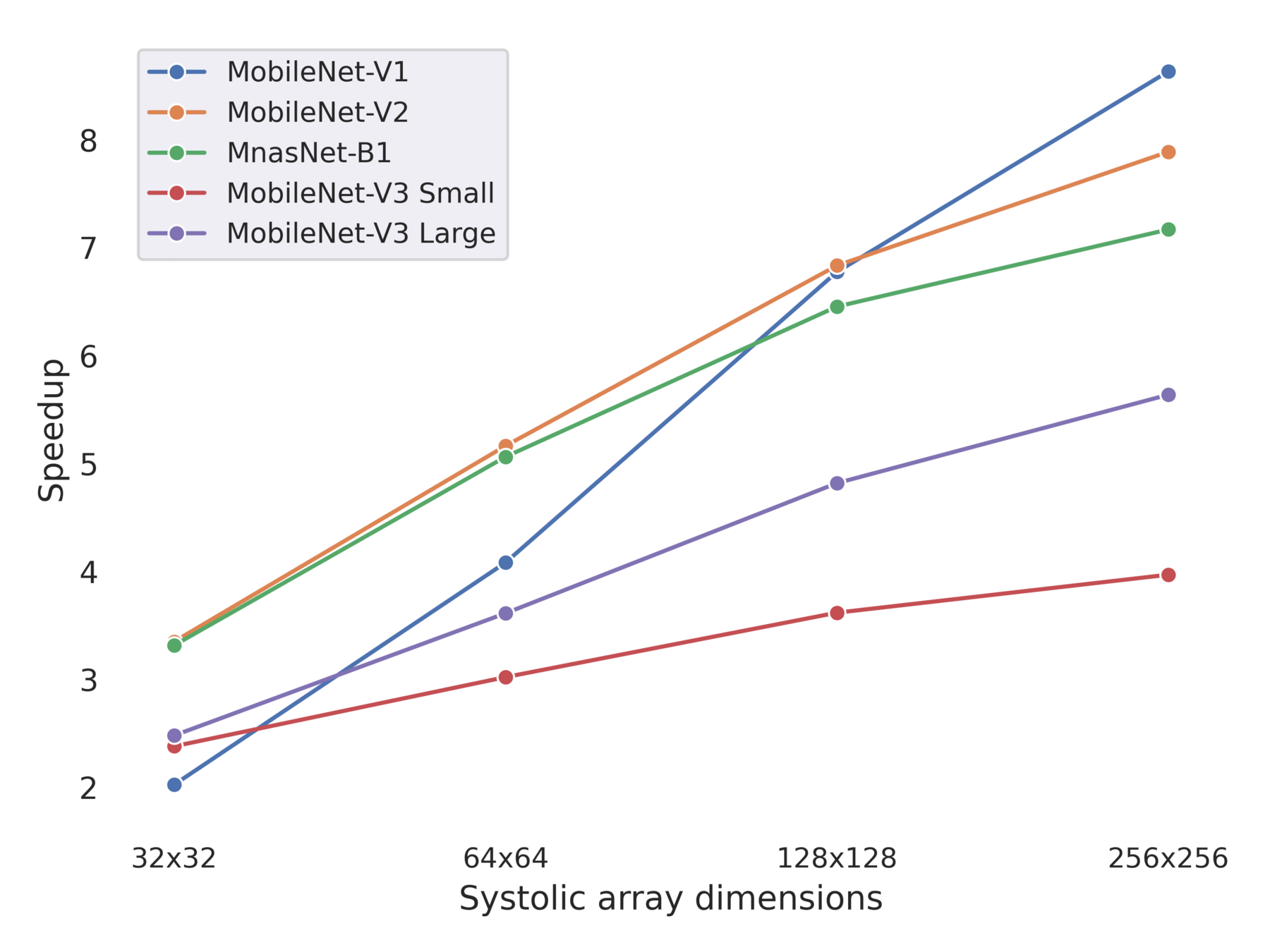
Scaling up of Speedup of Full FuSe variant wrt baseline
Multiple Trade-Offs solutions
DW Conv scales poorly !
Newer networks scales differently
Evaluation
Operator-wise Latency Distribution of Full FuSe Variants
Layerwise Speedup of MobileNet-V2 Full FuSe Variant
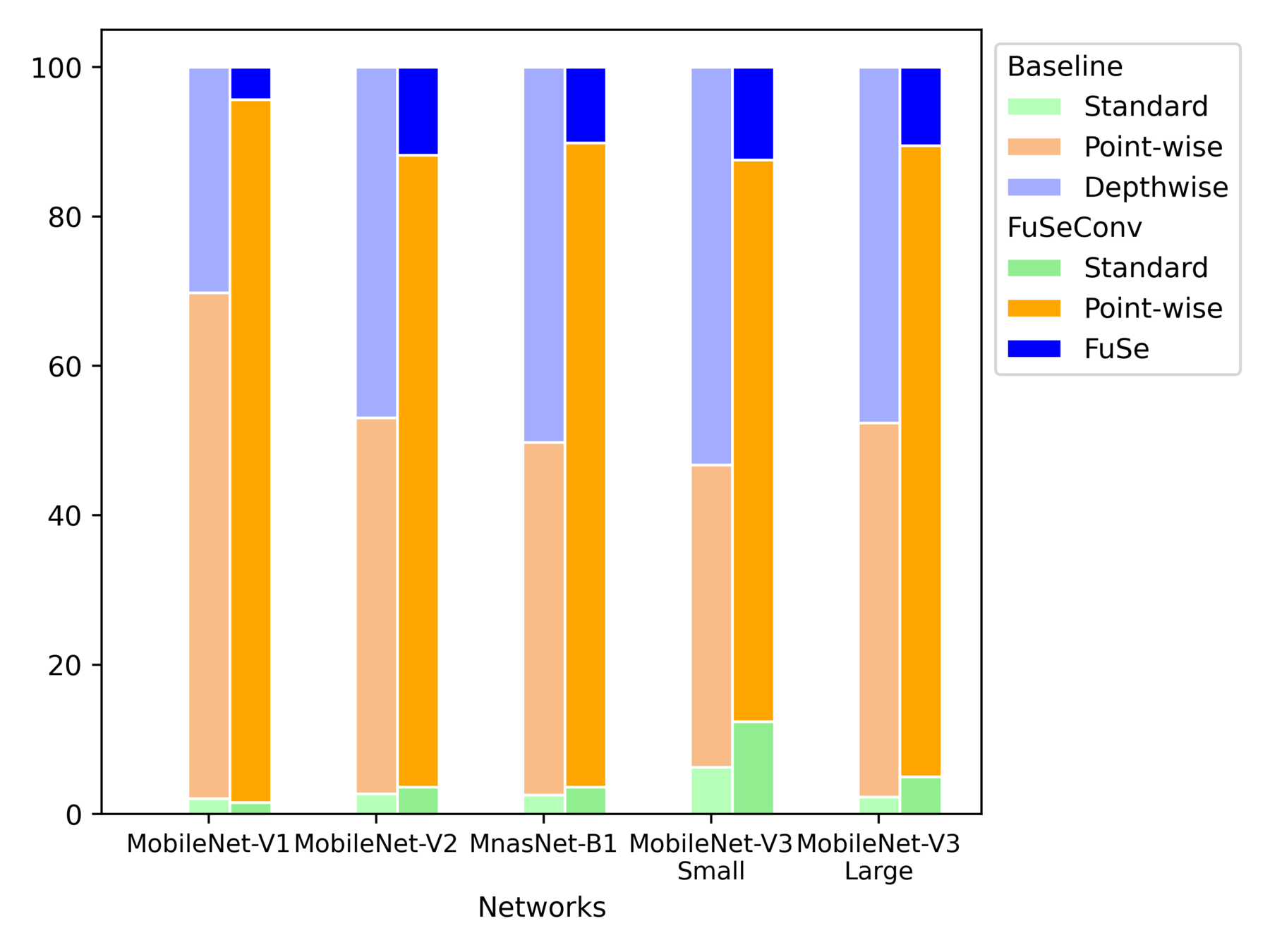
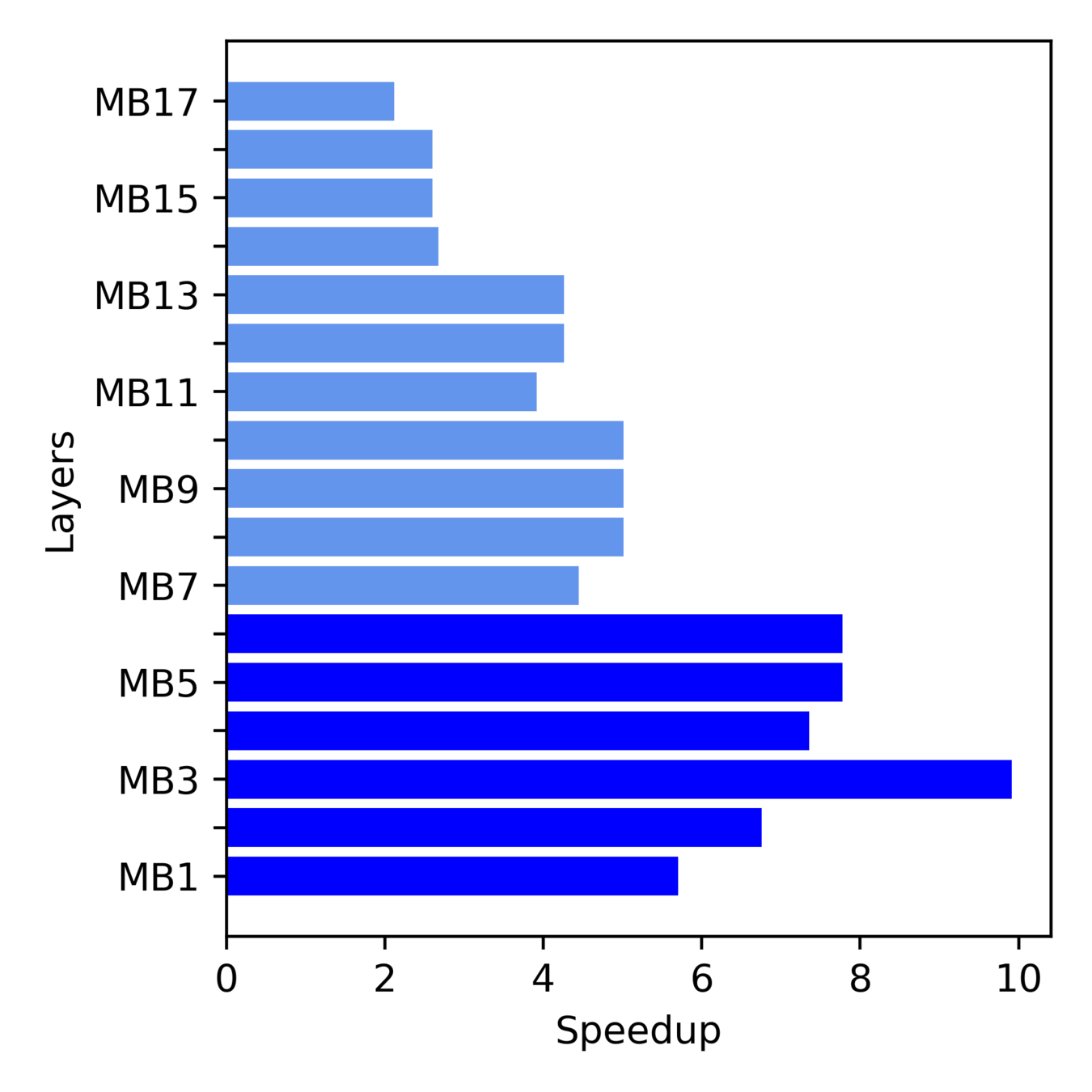
More Speedup from Initial layers
Inference latency dominated by Depthwise -> Point-wise
Summary
> Efficient Inference is still a crucial problem for DNN deployment. Currently proposed solutions are Hardware Accelerators and Efficient DNN Operator
> However, Depthwise Separable Convolutions are inefficient on Systolic Arrays and lacks data reuse to exploit parallelism
> We propose FuSeConv (Fully Separable 1D Convolutions) as a drop-in replacement for Depthwise Separable Convolutions
> Our Co-Design solution is atleast 4X faster than efficient mobile networks such as MobileNets and MnasNet with negligible accuracy-drop
> Motivates hardware-aware Neural Operator Search (NOS)
> We also proposed a 1D systolic dataflow for efficiently executing FuSeConv layers
Questions?
Reach me at selvams@purdue.edu
FuseConv_DATE_2021
By Vinod Ganesan
FuseConv_DATE_2021
Slides for Paper FuSeConv Fully Separable Convolutions for Fast Inference on Systolic Arrays
- 599



