Recent Advances in Randomized Caches
Systematic Analysis of Randomization-based Protected Cache Architectures
IEEE S&P, 2020
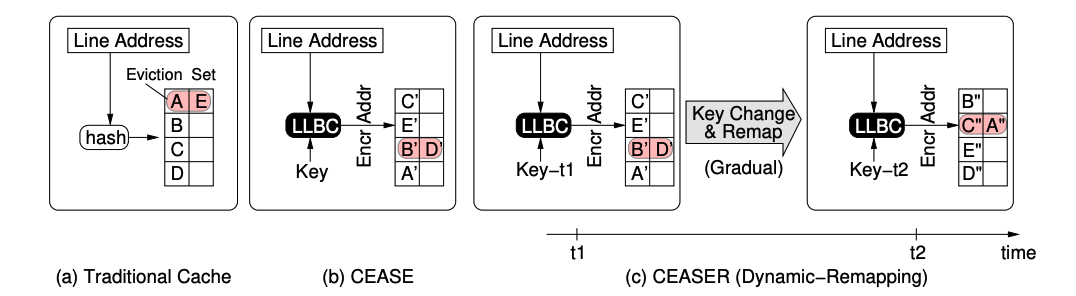
Randomized Caches
- Interference is a fundamental property in caches due to its finite size
- This interference can be exploited strategically to extract secret data - premise of cache side channels
- Randomized caches is a promising solution to mitigate it

- Can we accurately compare security levels for randomized caches?
- How realistic are security levels reported for secure randomized caches?
- Do secure randomized caches provide substantially higher security levels than regular caches?
Key Questions posed by the paper
Key Contributions of the paper
- Systematically cover the attack surface of randomized caches
- Propose and critically analyze generic randomized cache model that subsumes all proposed solutions in the literature
- PRIME+PRUNE+PROBE attack for randomized caches
Generic Randomized Cache Model
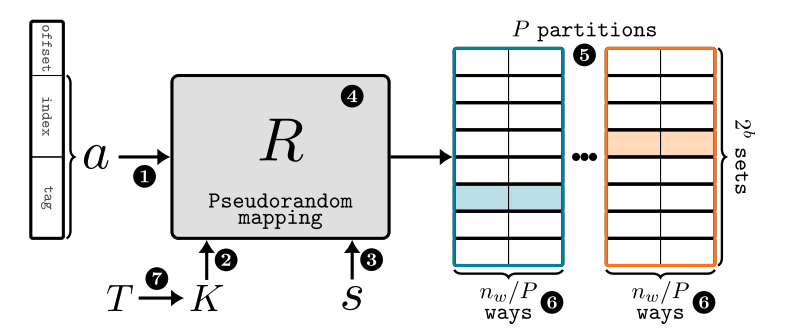
Memory Address: Physical or Virtual
Key to the mapper: Captures entropy!
Security domain separator: differentiating randomization for processes in different threat domains
Randomized Mapping \( R_K(a,s) \) following Kerchkoff's principle
Different partitions for the cache. Address a has different sets for each partition
Randomly selected partition based on R for storing and replacement
Rekeying Period

Classifying existing proposals on generic model
Attacker Model - Assumptions
- Attacker has full control over the address a
- The Key K is considered full-entropy i.e. TRNG
- If security domains are considered (s), the attacker can't get the same domain as victim
- The absolute output of R is non-observable. Only observable part is the cache contention
- Attacker cannot alter the rekeying condition
Attacker Models considered
- Ideal Black box attack: The mapping R behaves ideally; noise free system
- Non-ideal black box attack: Noise and multiple victim accesses
- Shortcut attacks: Internals of R are known to mount an attack
Exploiting Contention on Randomized Caches
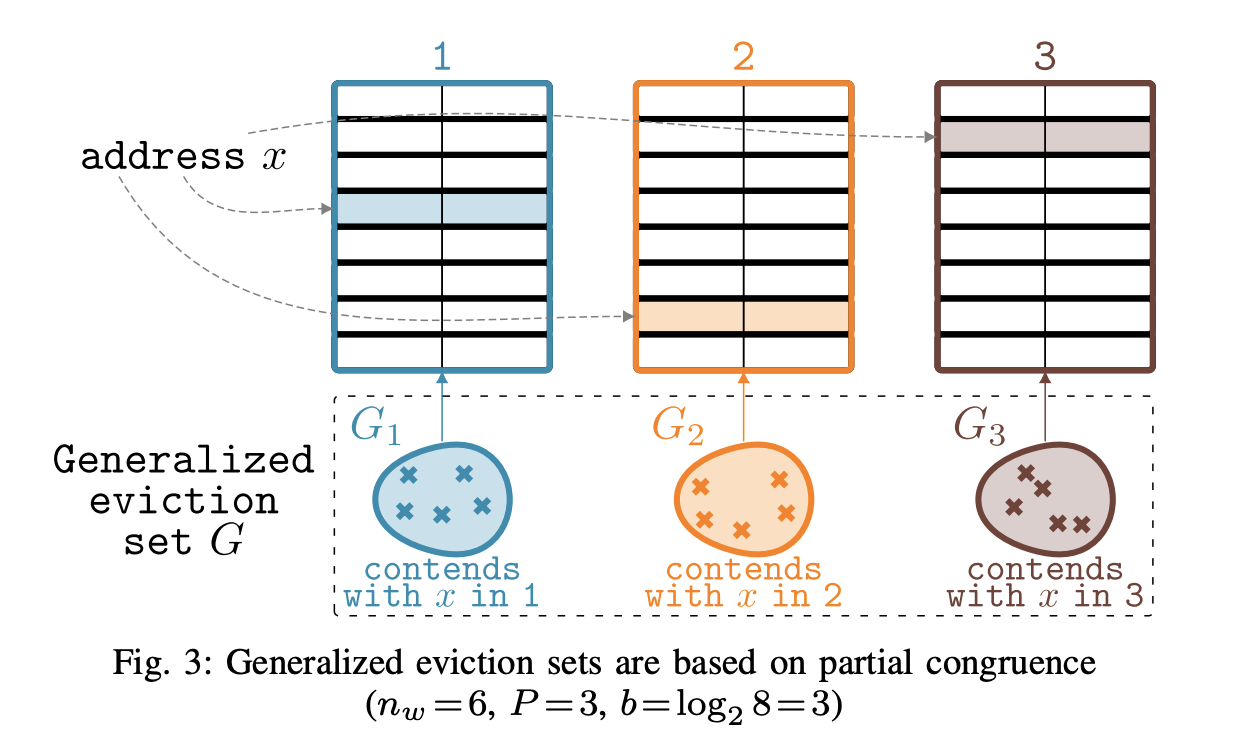
Generalized Eviction Set
\( G = \cup_{i=1}^P G_i \)
Eviction Probability
For Random Replacement
For \( G_i = \frac{|G|}{P}, 1\leq i \leq P \)
\( p_{rand}(|G|) = 1- (1 - \frac{1}{n_w})^{\frac{|G|}{P}} \)
For LRU
Binominal with \( \frac{|G|}{P} \) trials with \( \frac{n_w}{P} - 1 \) successes, and success probability \( \frac{1}{P} \)
\( p_{LRU}(|G|) \ = 1 - \sum_{i=0}^{\frac{n_w}{P}-1} {\frac{|G|}{P} \choose i} (\frac{1}{P})^i (1-\frac{1}{P})^{\frac{|G|}{P} - i} \)
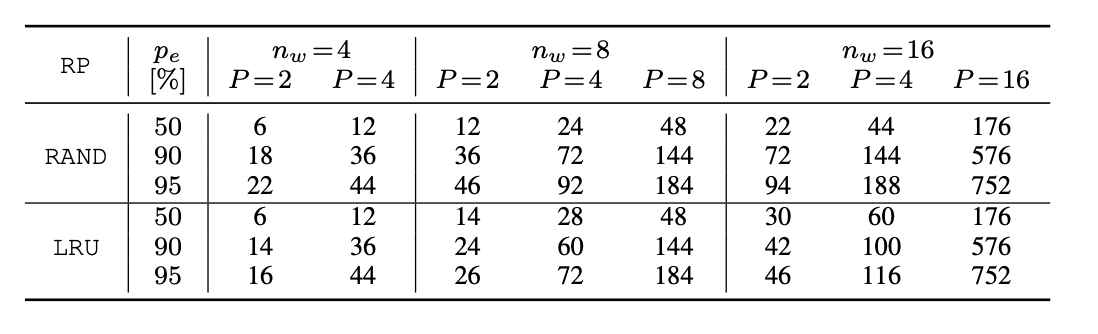
Generalized Eviction Set Size
Takeaway: Always rely on partial congruence!
Constructing Eviction Sets
- Once G is constructed, attacking is simple. But how to construct G?
- Conventionally, G is constructed by reducing a large set of addresses to a smaller set
- The authors suggest that a bottom-up approach will yield superior results for randomized caches
Prime + Prune + Probe
- In Prime step, the attacker accesses a set of k addresses
- In Prune step, the attacker re-accesses the set iteratively until there are no self-evictions
- Initially, if there are self-evictions the set is accessed again hoping that the eviction will go off
- If there is still a self-eviction that is detected - the corresponding accessed address is aggressively pruned from the eviction set
- Probe is the conventional method.

Check paper for more optimizations!
Lifting Idealizing Assumptions
- Victim accesses more addresses than just the target address x
- Static accesses -> accessing code and data section
- dynamic accesses -> data-dependent accesses
- The attacker cannot distinguish between the two
- Follow a two-phase approach
- Collect a super-set of addresses that collide with all static and dynamic addresses of the victim
- Form disjoint set of addresses for each target address
-
static addresses are statistically accessed more often
- This can be exploited and can be used to distinguish both by controlling the input
- Generate a histogram for all target addresses and eliminate the ones that are accessed more often!
Lifting Idealizing Assumptions
- System Noise is another major concern
- This can add uncertainties to the PRIME+PRUNE+PROBE
- Prune step might take out valuable candidates due to system noise
- Solution: Early-abort pruning. Don't go till all collisions are removed
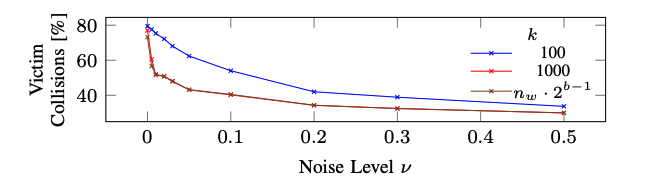
Shortcut Attacks
Refer to our work on BRUTUS!
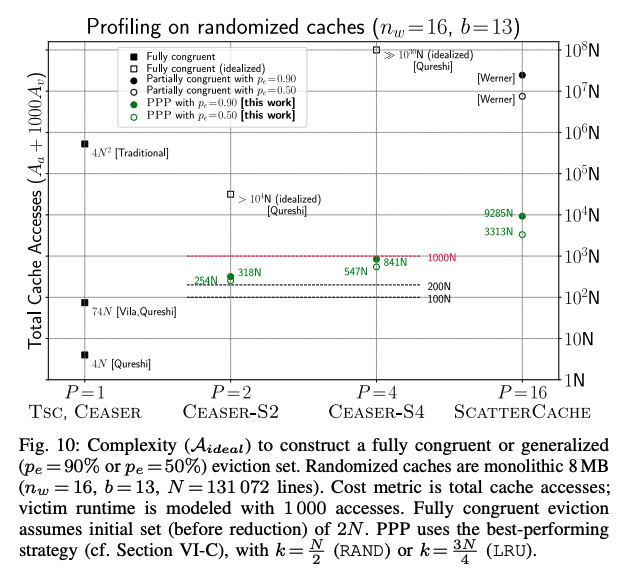
Number of Cache Accsses with PPP
Future Work Suggestions
- Stringent latency restrictions could inspire new and novel designs in low-latency cryptography
- The rekeying period may be varied for different security levels
- Cache attacks have two phases profiling (Eviction set building) and execution (P+P, P+P+P, E+R, F+R). The profiling space has a lot of opportunities for improvement
CaSA: End-to-end Quantitative Security Analysis of Randomly Mapped Caches
MICRO 2020
deck
By Vinod Ganesan
deck
- 258



