Параллельность прямых и плоскостей
10 класс
vkrysanov320@gmail.com
version 3.1, 02-10-2022
Задача 0
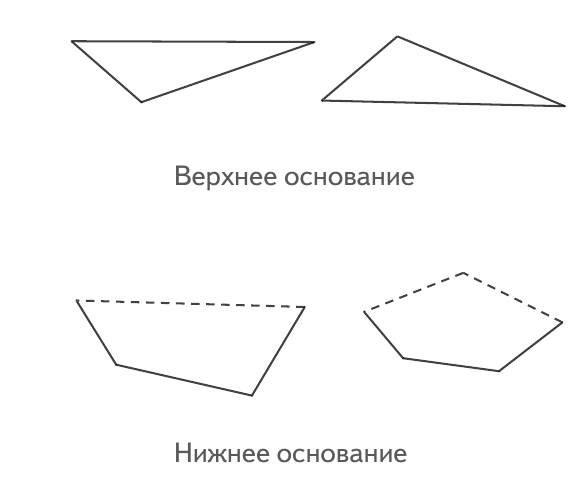
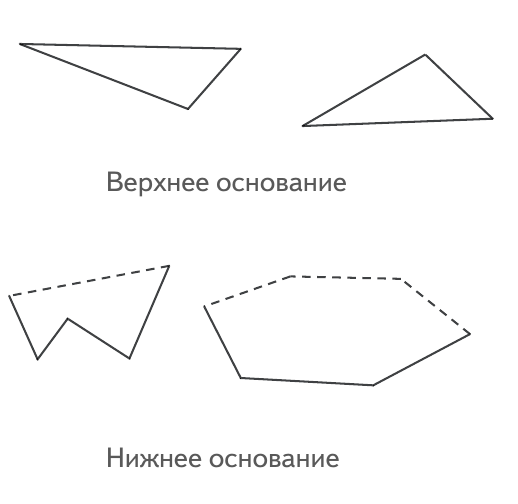
У призмы нарисовано верхнее или нижнее основание. Дорисуйте остальную часть, отметив невидимые ребра пунктиром:
а) прямой призмы;
б) косой призмы.
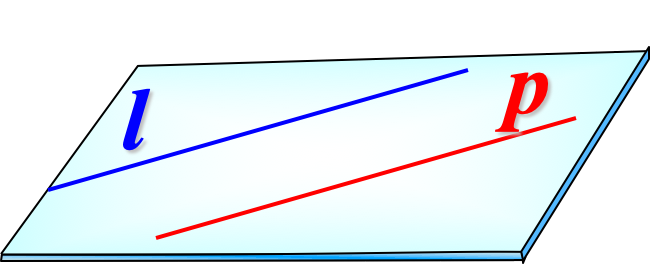
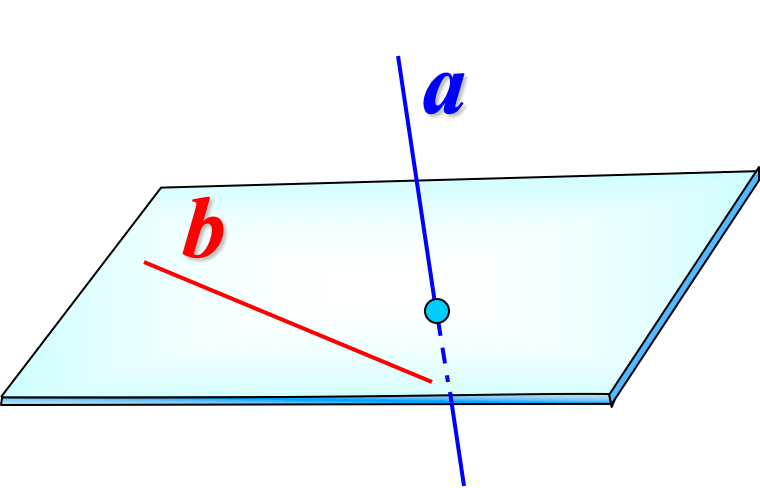
Три случая взаимного расположения прямых в пространстве
I.
II.
III.
Скрещивающиеся прямые:
Параллельные прямые:
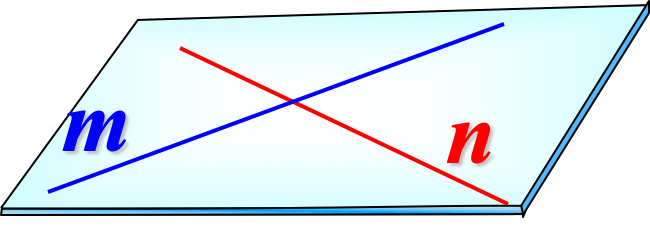
Пересекающиеся прямые:
I. Параллельность прямых, прямой и плоскости
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
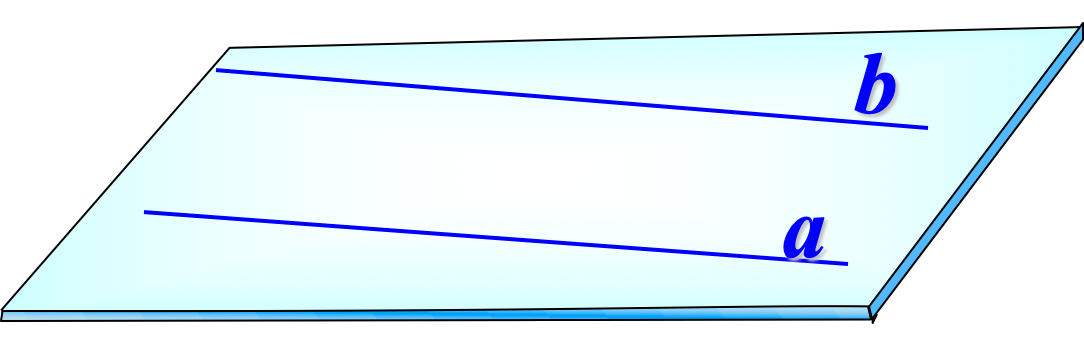
* Две параллельные прямые определяют плоскость.
Теорема:
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
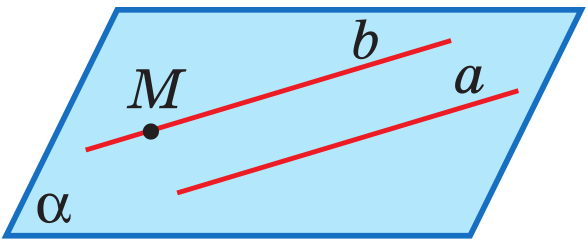
** Аксиома параллельности из планиметрии поможет доказать теорему о параллельных прямых в пространстве
Параллельные прямые в пространстве
Следствие из теоремы:
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Параллельные прямые на плоскости
Задача
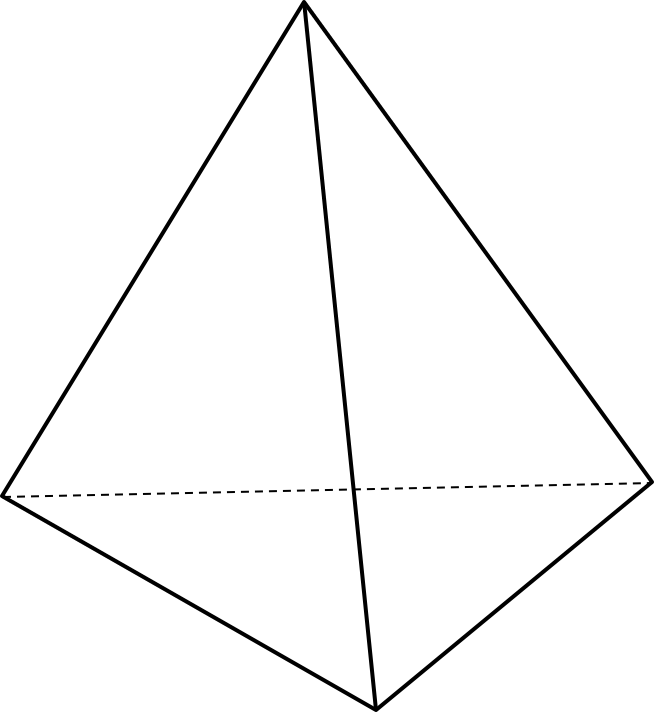
Точки — середины отрезков
соответственно.
Найти , если основание пирамиды — равносторонний треугольник, со стороной , а боковые ребра равны .
Параллельность трёх прямых
Лемма: Eсли одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема: Если две прямые параллельны третьей прямой, то они параллельны.
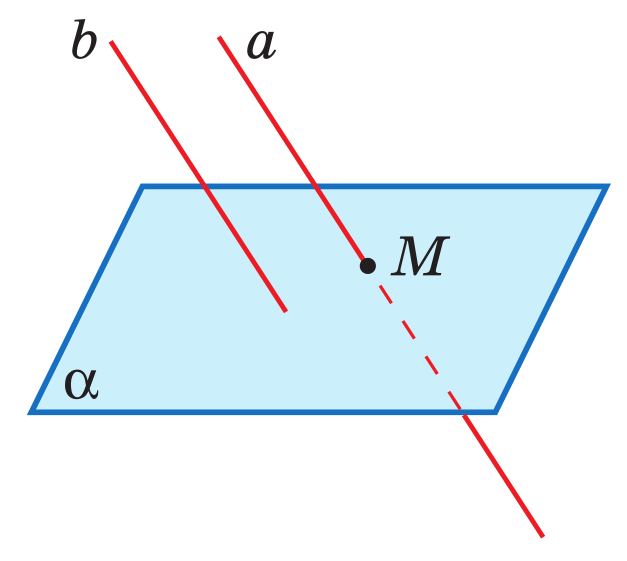
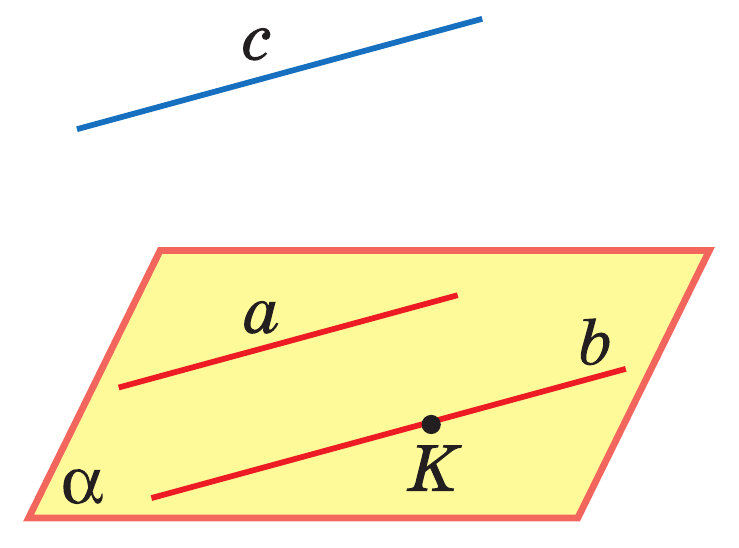
Задачи
1. — пространственный четырёхугольник.

Найти:
2.
Найти:
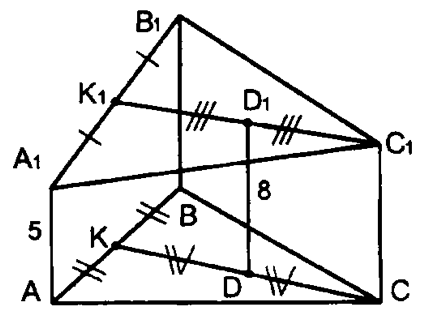
Задачи (2)
3. Дано:
Доказать: лежат в одной плоскости.
4(a). Нарисовать куб, прямоугольный параллелепипед, прямую треугольную призму и треугольную пирамиду. В каких из этих многогранников есть параллельные ребра. Подписать вершины многогранников и выписать по две пары параллельных ребер (если они есть).
4(b). Нарисовать куб и построить центры квадратов, являющихся его гранями. Нарисовать многогранник с вершинами в этих центрах.
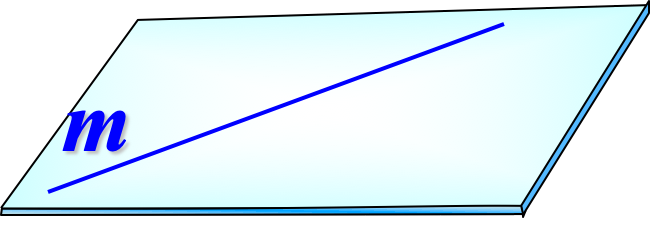

I.
II.
III.
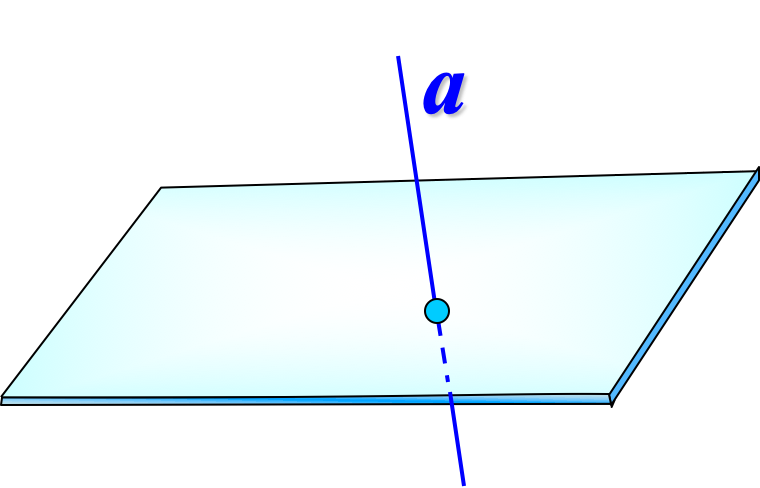
Прямая и плоскость имеют только одну общую точку (пересекаются):
Прямая и плоскость не имеют общих точек (параллельны):
Прямая лежит в плоскости:
Три случая взаимного расположения прямой и плоскости в пространстве
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек пересечения.
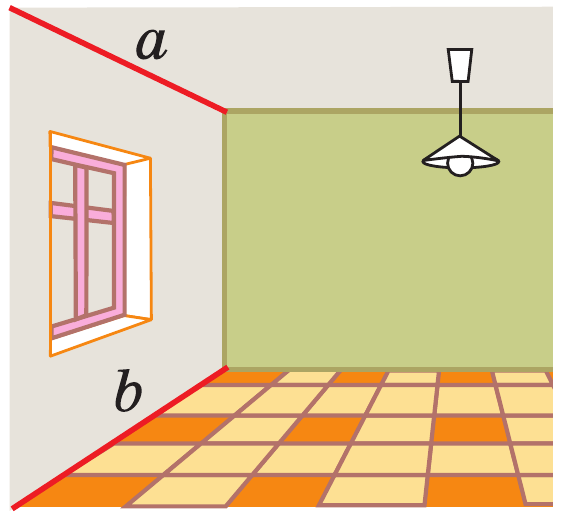
Теорема: Если прямая, не лежащая в данной плоскости, параллельна какой–нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Признак параллельности прямой и плоскости
Еще некоторые утверждения о параллельности прямой и плоскости
(1) Eсли плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
(2) Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Задачи
1. Точка лежит вне плоскости параллелограмма . Указать пары параллельных прямых и плоскостей.
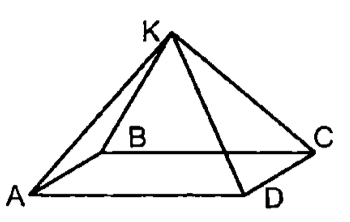
2. Точка лежит вне плоскости трапеции . Доказать:
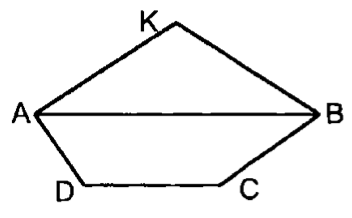
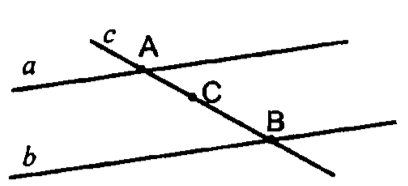
3. Точка лежит на отрезке , причем . Отрезок , равный , параллелен плоскости , проходящей через точку . Докажите, что прямая пересекает плоскость в некоторой точке , и найдите отрезок .
Задачи (2)
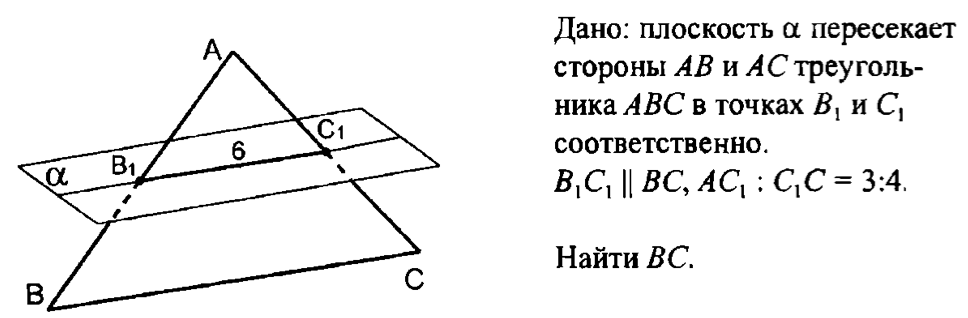
4. Плоскость пересекает стороны и треугольника в точках и соответственно.
Найти:
II. Скрещивающиеся прямые. Угол между прямыми
Скрещивающиеся прямые
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Теорема (признак скрещивающихся прямых): Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются.


обозначение
Теорема. На пару скрещивающихся прямых можно положить единственную пару параллельных плоскостей.
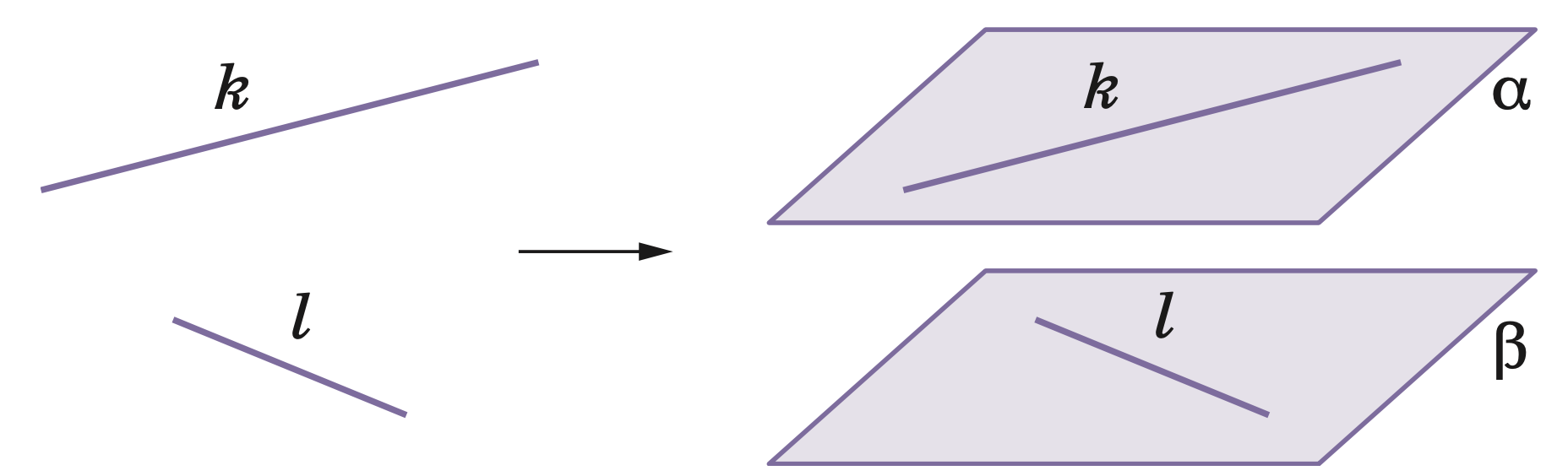
Угол между прямыми и скрщ. прямыми
Угол между прямыми — это такой угол , что .
Угол между прямыми — это такой угол , что .
Всегда рассматривается не тупой угол!
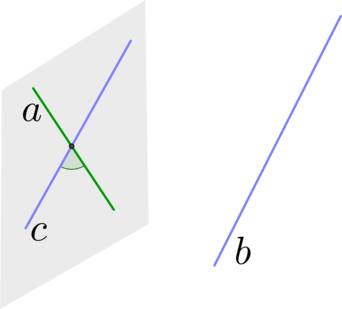
Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых провести плоскость, параллельную второй прямой (прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую , параллельную прямой ;
Шаг 3: тогда угол между прямыми и будет равен углу между прямыми и .
Задачи
Дан единичный куб :
1. Т.н.: .
2. Т.н.: .
3. Т.н.: .
4. Т.н.: .
5. Т.н.: .
6. Т.н.: .
Задачи (2)
Дана правильная треугольная призма, все ребра которой равны 1, :
1. Т.н.: .
2. Т.н.: .
3. Т.н.: .
4. Т.н.: .
5. Т.н.: .
6. Т.н.: .
Задачи (3)
1. Дана правильная треугольная пирамида с вершиной . Найти косинус угла между высотой основания и ребром , если сторона основания равна , а боковое ребро равно .
Дана правильная шестиугольная призма, все ребра которой равны 1, :
2. Т.н.: .
3. Т.н.: .
4. Т.н.: .
5. Т.н.: .
6. Т.н.: .
7. Т.н.: .
III. Параллельность плоскостей
Случаи взаимного расположения плоскостей
I.
II.
Параллельные плоскости:
Пересекающиеся плоскости:
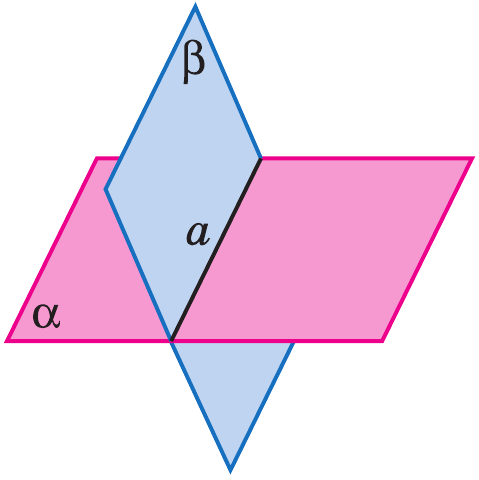
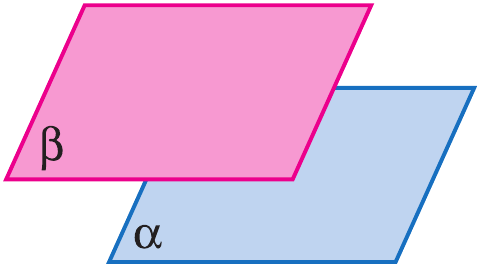
Две плоскости называются параллельными, если они не пересекаются.

Параллельные прямые в пространстве

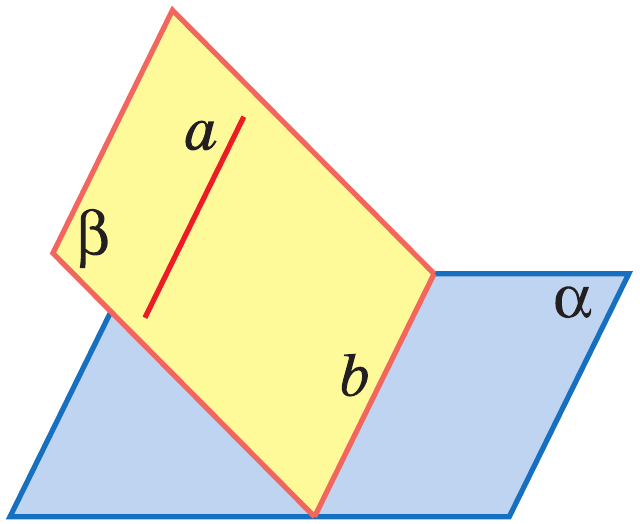
Теорема: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
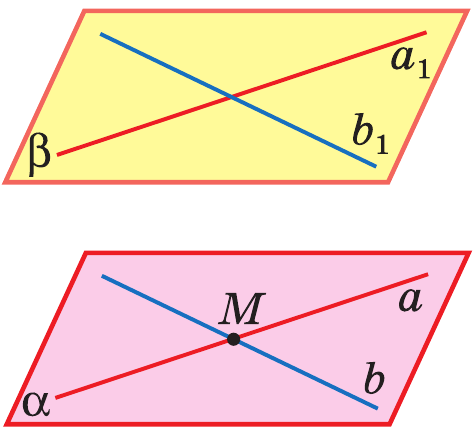
I. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Свойства параллельных плоскостей
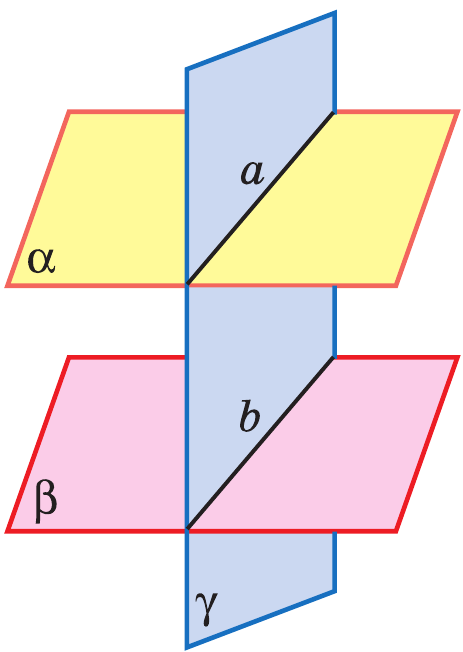
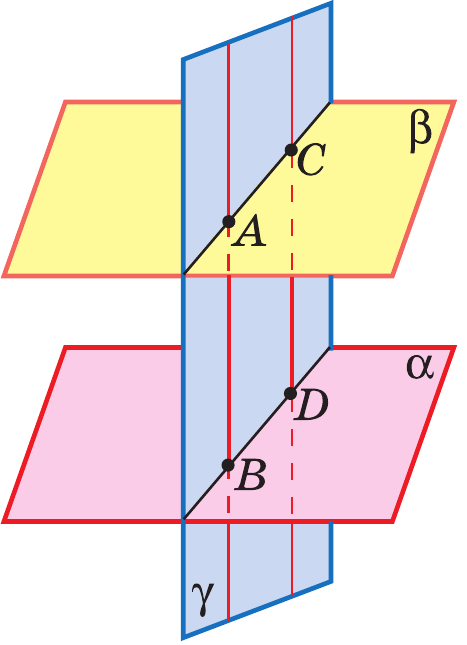
II. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Теорема Фалеса *
Параллельные прямые отсекают на секущих пропорциональные отрезки.
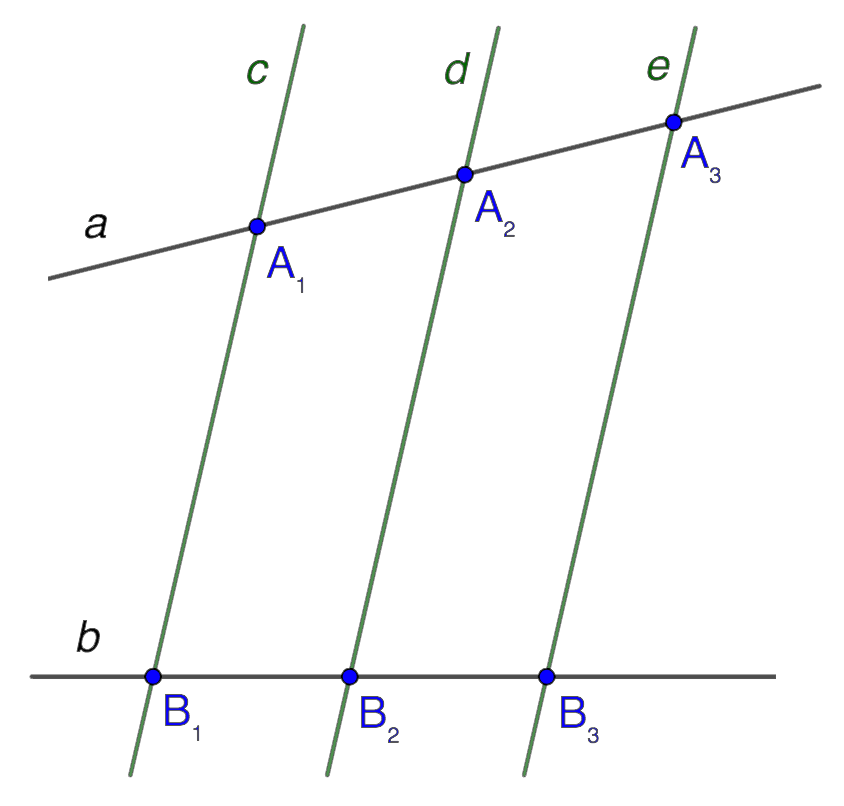
Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные.
Задачи
1.
Доказать:
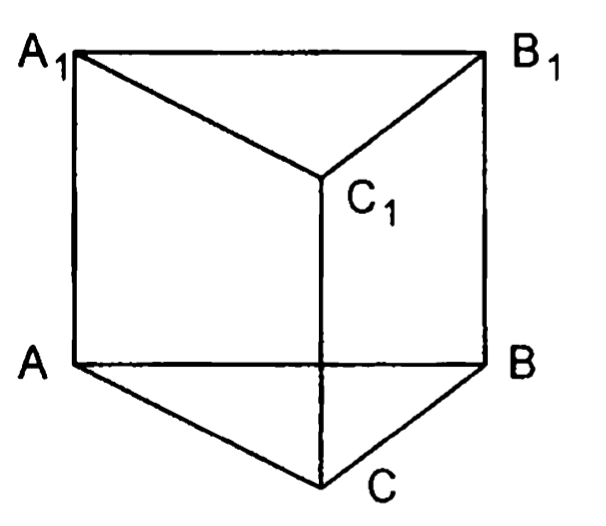
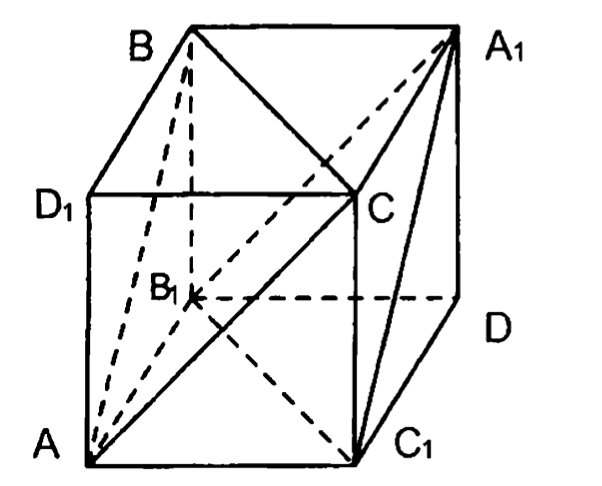
2. — куб.
Доказать:
Задачи (2)
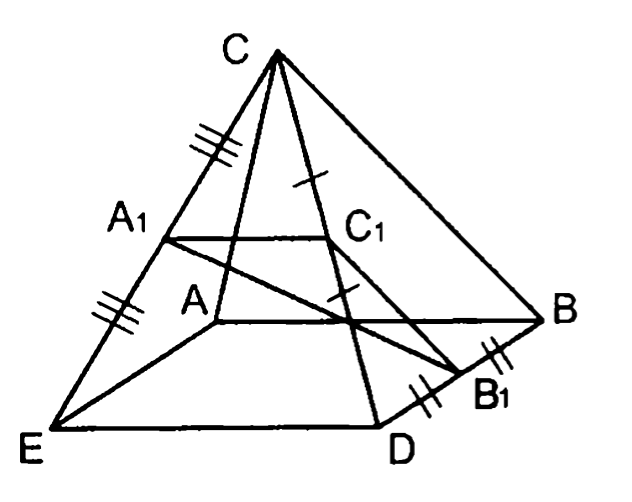
3. — параллелограмм.
Доказать:
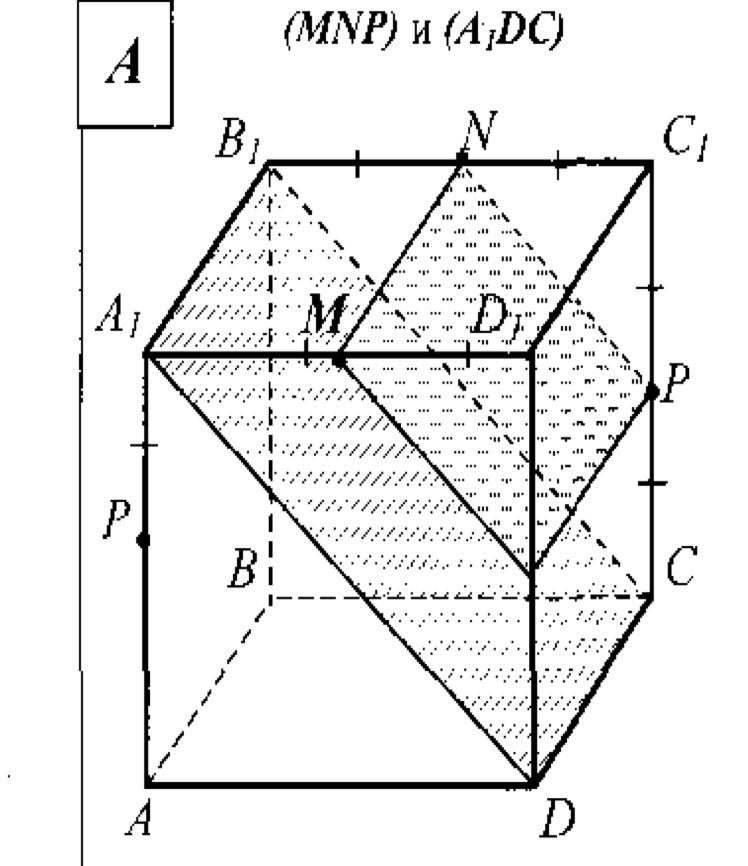
4. — куб.
Доказать:
Задачи (3)
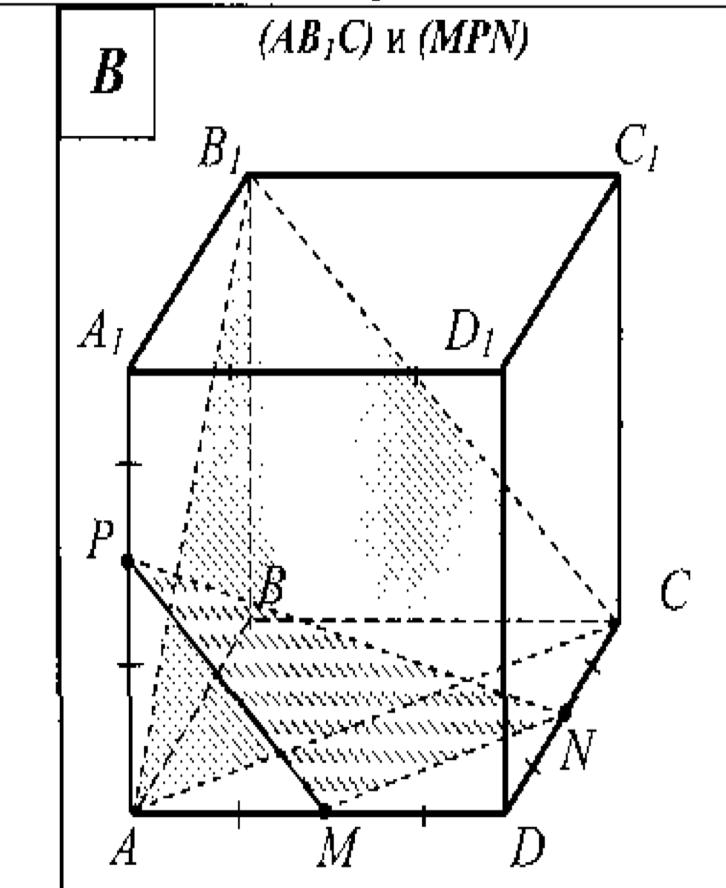
5. — куб.
Доказать:
6. Изобразить параллелепипед и отметить внутреннюю точку грани Построить сечение параллелепипеда, проходящее через точку параллельно:
а) плоскости основания ;
б) грани ;
в) плоскости .
Задачи (4)
7. Плоскости и параллельны. Прямая пересекает плоскости и соответственно в точках и , а параллельная ей прямая — соответственно в точках и . Доказать, что отрезки и равны.
8. Точка не лежит в плоскости треугольника , точки , и — середины отрезков , и соответственно.
а) Доказать .
б) Найти , если .
9. Доказать, что в параллелепипеде плоскость параллельна плоскости .
Задачи (5)
10. Параллельные плоскости и пересекают сторону угла соответственно в точках и , а сторону этого угла — соответственно в точках и .
а) Найти и , если , , .
б) Найти и , если , , .
11. На трёх лучах, исходящих из точки и не лежащих в одной плоскости, взяты отрезки , , такие, что
. Доказать, что:
a) ;
б) ;
в) прямая пересечения плоскостей и параллельна плоскостям и .
Г1. Параллельность прямых и плоскостей
By vkrysanov320
Г1. Параллельность прямых и плоскостей
- 1,593



