Зачем изучать математику?
10 класс
vkrysanov320@gmail.com
version 3.5, 31-09-2024Парадокс познания:
«Чем больше мы знаем, тем больше мы не знаем.»
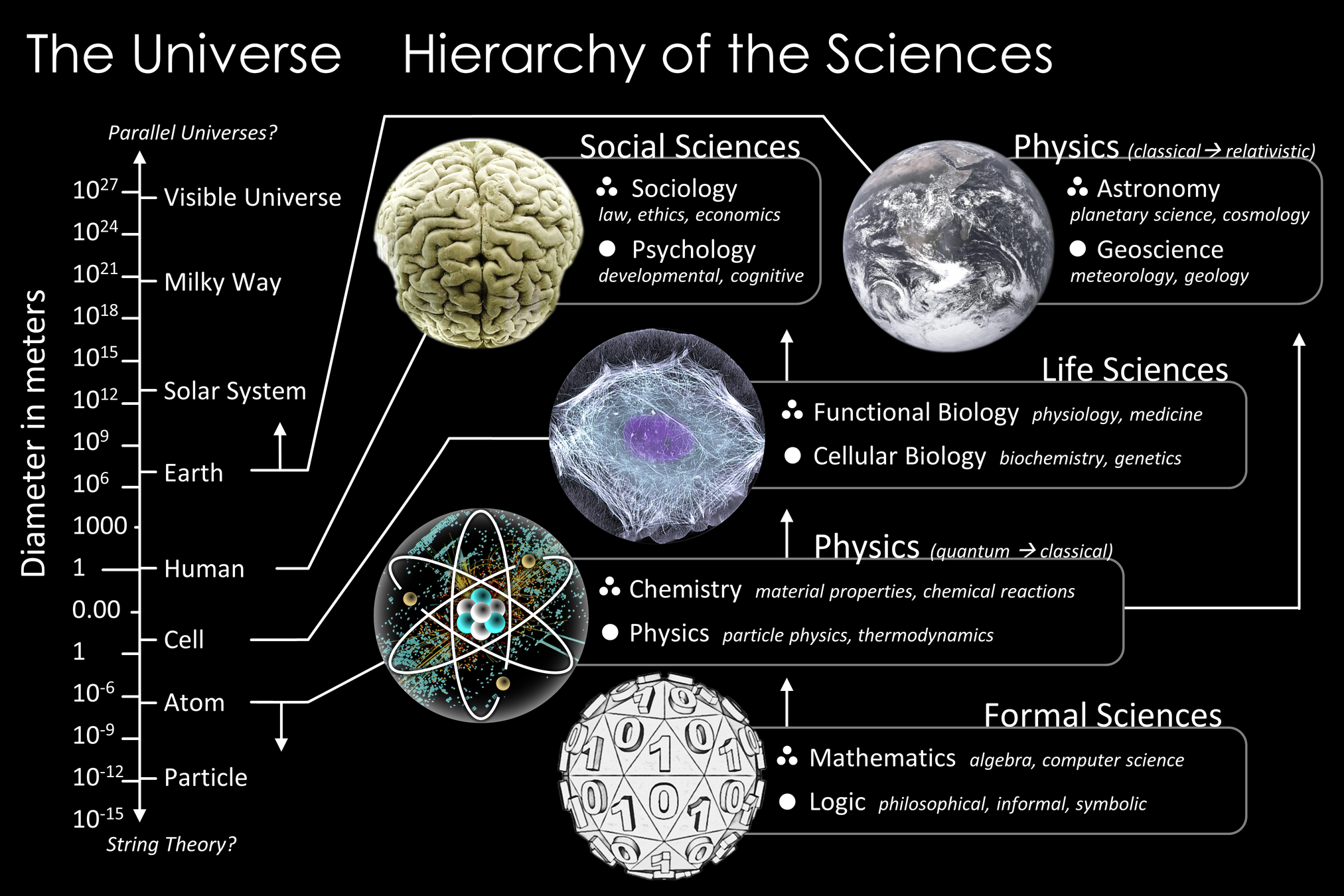
Математика в системе наук
Проверим внимательность...
Сколько будет ?
2^2
Сколько будет ?
3^2
Сколько будет ?
4^2
А чему равен угол в квадрате?
Следователь Петров хочет установить по фотографии куда ехал автобус. Как это сделать?
Следователь Петров хочет установить по фотографии куда ехал автобус. Как это сделать?
Дверь с правой стороны
Простоя геометрическая задачка
A
C
B
H
AB = 10;
CH= 6;
т.н.:
S(ABC)
Простоя геометрическая задачка (2)
AB = 10;
CH= 6;
т.н.:
S(ABC)
\begin{cases}
\\
\\
\end{cases}
\begin{cases}
\\
\\
\end{cases}
\begin{cases}
\\
\\
\\
\\
\\
\end{cases}
10-a
a
6
\begin{cases}
(10-a)^2 + 6^2 = AC^2;\\
a^2 + 6^2 = BC^2;\\
AC^2 + BC^2 = AB^2;
\end{cases}
Применив теорему Пифагора:
a^2 + (10-a)^2 + 72 = 100
a^2 + 100 - 20a + a^2 + 72 = 100
2a^2 - 20a + 72 = 0
a^2 - 10a + 36 = 0
D = 100 - 4\cdot36 < 0
\begin{cases}
a^2 + (10-a)^2 + 72 = AC^2 + BC^2;\\
AC^2 + BC^2 = 100;
\end{cases}
\Rightarrow a \notin \mathbb{R}
S(ABC) = \frac{1}{2} AB \cdot CH = \frac{1}{2} \cdot 10 \cdot 6 = 30.
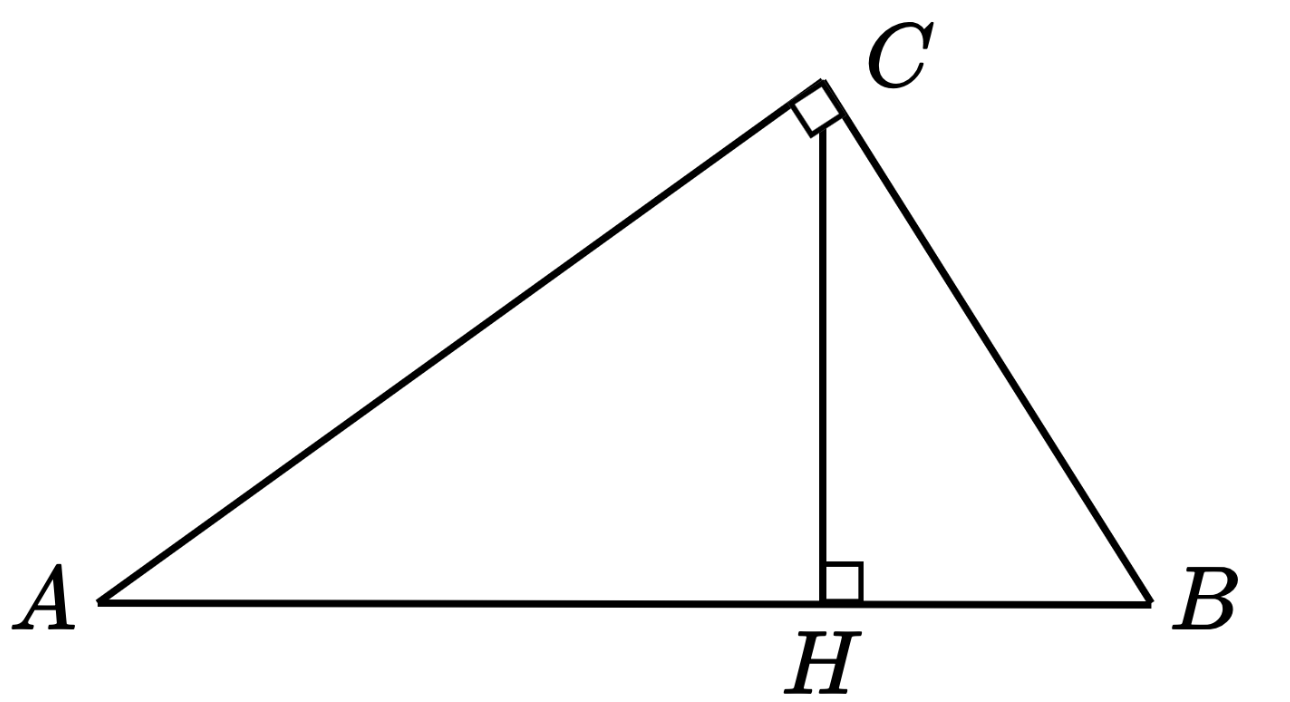
Тривиальное решение:
— но неверное!
\Rightarrow S(ABC) \in \varnothing.
а вот почему ...
Под крылом самолета
Самолёт покрывает расстояние от города А до города Б в 1 час 20 минут. Однако обратный перелет он совершает в 80 минут. Как вы это объясните?
Под крылом самолета. Ответ
А то объяснять??? То что 80 минут и 1 час 20 минут — это одно и то же?
Чему равна сумма чисел
от 1 до 100?
Сумма чисел от 1 до 100
S_{n} = \frac{a_1 + a_n}{2} \cdot n \Rightarrow S_{100} = \frac{1 + 100}{2} \cdot 100 = 5050.
По формуле суммы арифметической прогрессии:
... или более простым путем:
1
2
3
49
51
97
98
99
...
...
+ 50
\underbrace{\text{\hspace{4.5cm}}}
+ 100
49 \cdot 100
\sum = 100 + 49 \cdot 100 + 50 = 5050.
А теперь совсем чуть-чуть посложнее...
Вычислить в уме
a)\text{ }0{,}75 \cdot \frac{3}{4}
b)\text{ }-3{,}5 + \frac{7}{2}
c)\text{ }(\sqrt{144})^2
d)\text{ }0{,}25 \cdot 19 \cdot 4
e)\text{ }\sqrt{81} - 2^4
f)\text{ }6^3 \cdot 6^{-3}
g)\text{ }1{,}5 \cdot \frac{4}{3}
j)\text{ }-1{,}25 + \frac{5}{4} + 3
k)\text{ }(\sqrt{3})^4
l)\text{ }3^7 \cdot 3^{-4}
m)\text{ }(-3\frac{1}{3})^3
n)\text{ }2{,}5 \cdot 0{,}4
o)\text{ }(\sqrt{4})^6
p)\text{ }\sqrt{1\frac{9}{16}}
i)\text{ }0{,}3 \cdot \frac{10}{3} : 0{,}2
h)\text{ }(-1\frac{1}{2})^2
Вычислить без использования вычислительных средств
5678901011^2 - 5678901010 \cdot 5678901012 = ?
(a - b)(a + b) = a^2 - b^2
Приведём выражение к «нужному» виду. По формуле сокращённого умножения получим:
5678901011^2 - 5678901010 \cdot 5678901012 =
= 5678901011^2 - [(5678901011 - 1)(5678901011 + 1)] =
= 5678901011^2 - 5678901011^2 + 1 = 1.
5678901011^2 - 5678901010 \cdot 5678901012 = ?
Вычислить без использования вычислительных средств. Решение
19911991 \cdot 199219921992 - 19921992 \cdot 199119911991 = ?
Вычислить без использования вычислительных средств (2)
19911991 \cdot 199219921992 - 19921992 \cdot 199119911991 = ?
1991 \cdot 10001
1992 \cdot 100010001
{\underbrace{19911991 \cdot 199219921992}_{1991 \cdot 1992 \cdot 10001 \cdot 100010001}} - {\underbrace{19921992 \cdot 199119911991}_{1992 \cdot 1991\cdot 10001 \cdot 100010001}} = 0.
Вычислить без использования вычислительных средств (2). Решение
Вычислить
24\frac{3}{4} - \Bigl(12\frac{5}{9} - 4\frac{7}{8} + 1\frac{5}{12}\Bigr) - \Bigl(13\frac{15}{16} - 10\frac{5}{9} \Bigr) - 2\frac{13}{48};
\frac{\bigl(15: \frac{5}{18} : 3\frac{3}{8}\bigr) \cdot \bigl(\frac{1}{16} + \frac{11}{36} + \frac{5}{48} + \frac{5}{18} \bigr)}{\bigl(11\frac{5}{11} - 8\frac{21}{22}\bigr): 1\frac{2}{3}};
\Bigl(\frac{928 \cdot 10^{-2}}{0{,}8} - 0{,}6\Bigr): \Bigl[\frac{\bigl(42 \cdot 3\frac{5}{6} + 3{,}3 : 0{,}03 \bigr) : \frac{1}{15}}{\bigl( 3\frac{3}{4} : 0{,}625 - 0{,}84 : 0{,}8 \bigr) : 0{,}03} \Bigr]^{-1}.
а)
б)
в)
Вычислить. Ответы
24\frac{3}{4} - \Bigl(12\frac{5}{9} - 4\frac{7}{8} + 1\frac{5}{12}\Bigr) - \Bigl(13\frac{15}{16} - 10\frac{5}{9} \Bigr) - 2\frac{13}{48} = 10;
\frac{\bigl(15: \frac{5}{18} : 3\frac{3}{8}\bigr) \cdot \bigl(\frac{1}{16} + \frac{11}{36} + \frac{5}{48} + \frac{5}{18} \bigr)}{\bigl(11\frac{5}{11} - 8\frac{21}{22}\bigr): 1\frac{2}{3}} = 8;
\Bigl(\frac{928 \cdot 10^{-2}}{0{,}8} - 0{,}6\Bigr): \Bigl[\frac{\bigl(42 \cdot 3\frac{5}{6} + 3{,}3 : 0{,}03 \bigr) : \frac{1}{15}}{\bigl( 3\frac{3}{4} : 0{,}625 - 0{,}84 : 0{,}8 \bigr) : 0{,}03} \Bigr]^{-1} = 271.
а)
б)
в)
A
B
Сколько путей ведет
из A в B?
A
B
Сколько путей ведет из A в B? Решение
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
6
10
15
21
10
20
35
56
Ответ: 56.
n
m
n+m
Для каждой вершины будет работать следующее правило (метод динамического программирования):
А вот еще геометрическая задачка...
Пластина имеет форму круга, в котором вырезано круглое отверстие меньшего радиуса так, что окружности, являющиеся границами кругов, касаются друг друга. Длина хорды большей окружности, которая параллельна их общему диаметру и касается меньшей окружности, равна 6 см. Найдите площадь пластины.
Геометрическая задачка (2). Решение
r
R
A
B
C
D
O
AO \cdot OB = CO \cdot OD;
6
\underbrace{\text{\hspace{1.5cm}}}
S = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) = 9 \pi.
3 \cdot 3 = (R - r)(R+r);
9 = R^2 - r^2.
Посетитель пришёл в музей и увидел в музее странные часы (рисунок справа). На их циферблате нет цифр и вообще не понятно, где у часов верх. А секундная, минутная и часовая стрелки имеют одинаковую длину. Какое время показывали часы?
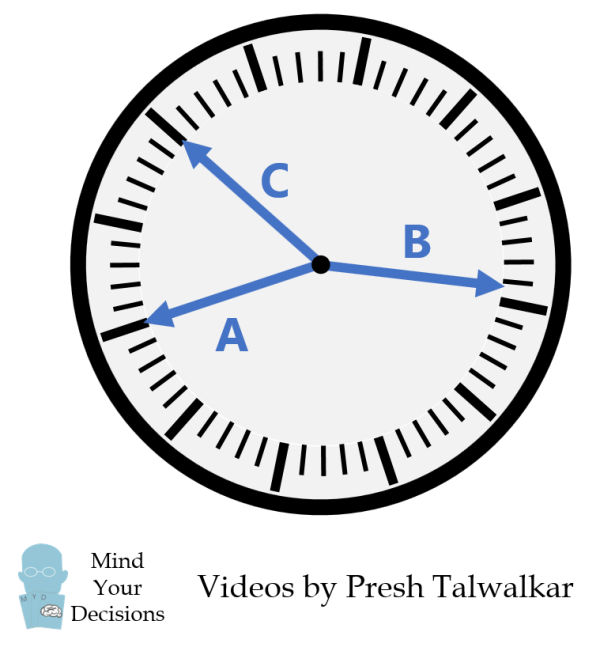
Странные часы
Странные часы. Часовая стрелка
B — часовая стрелка. Так как, если бы часовая стрелка смотрела ровно на часовую отметку, минутная и секундная стрелка смотрели бы ровно на отметку «12».
Странные часы. Где «12»?
Оставшиеся две стрелки указывают ровно на часовые отметки, поэтому сейчас сколько-то часов и целое число минут — в частности, секундная стрелка указывает на отметку «12».
Какая стрелка минутная а какая секундная?
12?
12?
Странные часы. Два варианта
12
12
2
10
7
5
Рассматриваем два случая:
Если секундная стрелка — стрелка А, то на часах немного меньше семи часов (судя по часовой стрелке), и по минутной стрелке — 10 минут, что невозможно.
Странные часы. Ответ
12
10
5
Так образом, B — часовая стрелка. А — минутная, С — секундная.
4:50
16:50
или
Время на часах:
И совсем легенькая геометрическая задачка ...
Возьмем квадрат со стороной и, следовательно, с площадью . Разрежем его на три части так, как показано на первом чертеже. Затем переложим эти части так, как показано на втором. Получается прямоугольник, площадь которого легко вычислить:
8 \text{ см}
64 \text{ см}^2
S = 7 \text{ см} \cdot 9 \text{ см} = 63 \text{ см}^2.
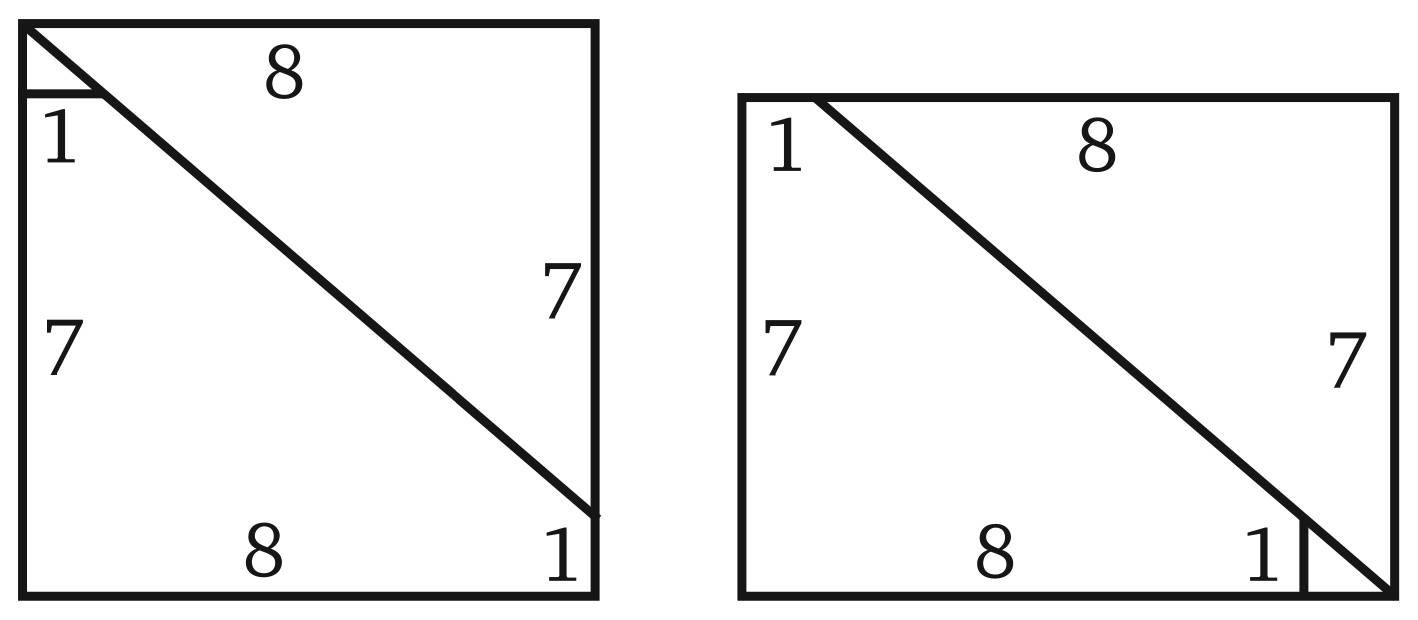
В чем же дело?
Метро в Запрещаевске
В городе Запрещаевске в метро строго запрещено провозить предметы, длина, ширина или высота которых превосходит 1 м. Тем не менее первокласснику Васе удалось провезти лыжи длиной 1,5 м. Как?
Задача про автобус
Весь путь автобус ехал с неизменной скоростью. В первую часть пути автобус проехал столько километров, сколько минут ему осталось ехать. Во вторую часть пути автобус проехал столько километров, сколько минут ехал в первую часть пути. Какова скорость автобуса?
Задача про автобус. Решение
Весь путь автобус ехал с неизменной скоростью. В первую часть пути автобус проехал столько километров, сколько минут ему осталось ехать. Во вторую часть пути автобус проехал столько километров, сколько минут ехал в первую часть пути. Какова скорость автобуса?
\underbrace{\text{\hspace{4.5cm}}}
\underbrace{\text{\hspace{3.8cm}}}
x \text{ км}
y \text{ км}
y \text{ мин}
x \text{ мин}
\Rightarrow
\Rightarrow
\frac{x}{y}
\frac{y}{x}
\text{км/мин}
\text{км/мин}
\Rightarrow \frac{x}{y} = \frac{y}{x} = 1 \text{ км/мин} = 60 \text{ км/ч}.
Ответ: 60 км/ч.
A
B
... и опять про автобус
Дорога между двумя горными селами A и B идет то в гору, то под гору. Старый автобус, который развивает среднюю скорость 30 км/ч в гору и 60 км/ч под гору, проехал из A в B и обратно. Какова была его средняя скорость на всем пути?
A
B
... и опять про автобус. Решение
A
B
\underbrace{\text{\hspace{13cm}}}
S
S
км — проехал в гору,
S
км — проехал с горы (ехал туда-обратно же).
\Rightarrow v_{\text{ср}} = \frac{\sum s_{i}}{\sum t_{i}} = \frac{2S}{\frac{S}{30} + \frac{S}{60}}
= \frac{2S}{\frac{2S + S}{60}} = \frac{2S \cdot 60}{3S} = 40 \text{ км/ч}.
Ответ: 40 км/ч.
«Реактивная муха»
Два города А и В находятся на расстоянии 300 км друг от друга. Из этих городов одновременно выезжают друг другу навстречу два поезда и мчатся, не останавливаясь, со скоростью 50 км/ч. В начальный момент движения поезда из пункта А взлетает муха и принимается летать вперед и назад между поездами, пока те не встретятся, со скоростью 1000 км/ч. Сколько километров пролетела муха?
0. Зачем изучать математику
By vkrysanov320
