Algorithms #7
Stack & Queue

Stack
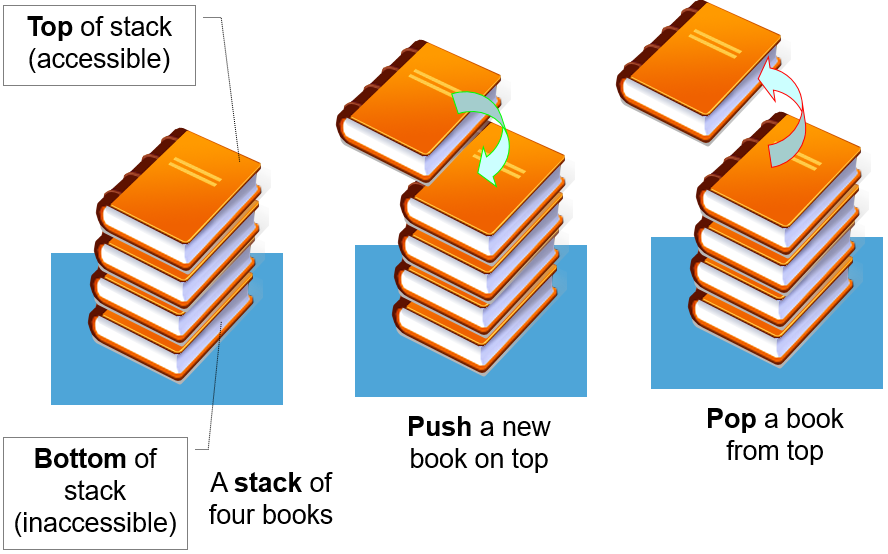
Stack is a linear data structure which follows a particular order in which the operations are performed.
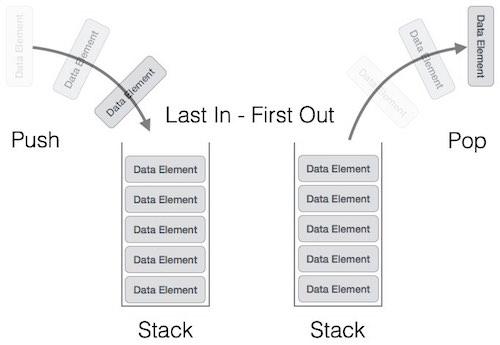
Stack LIFO
The order in which elements come off a stack gives rise to its alternative name, LIFO (last in, first out)

Stack operations
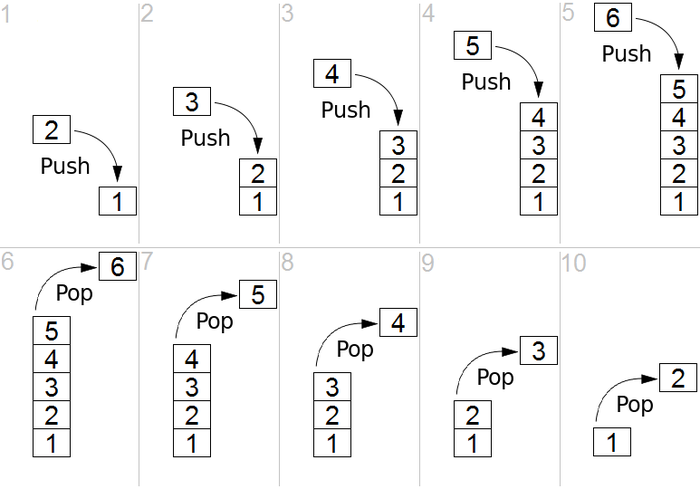
push(x) places the item x onto the top of the stack
pop() removes the top item from the stack, and returns that item.
Usages of Stack
- DFS (Depth First Search) on tree / graph datastructures
- During Function Calls (Call Stack in JS)
- AST processing / Syntax parsing
- Browser back-forth button (JS History API).
- Reversing a string
- Converting expressions(prefix-infix-postfix)
- Recursive functions.
- Maintaining any sort of LIFO data.
- And many more...
Problem #1
Implement string stack using only string operations
const stack = new StringStack();
stack.push("one");
stack.push("two");
stack.push("three");
stack.pop() // threeProblem #2
Implement string stack using linked list
const stack = new Stack();
stack.push("one");
stack.push("two");
stack.push("three");
stack.pop() // threeProblem #3
Implement string stack using linked list
function validateBrackets(ext) {
...
}
validateBrackets("[(1 + 1)]^2"); // true
validateBrackets("(1 + [2 *) - 1]"); // false
validateBrackets("({[]})"); // true 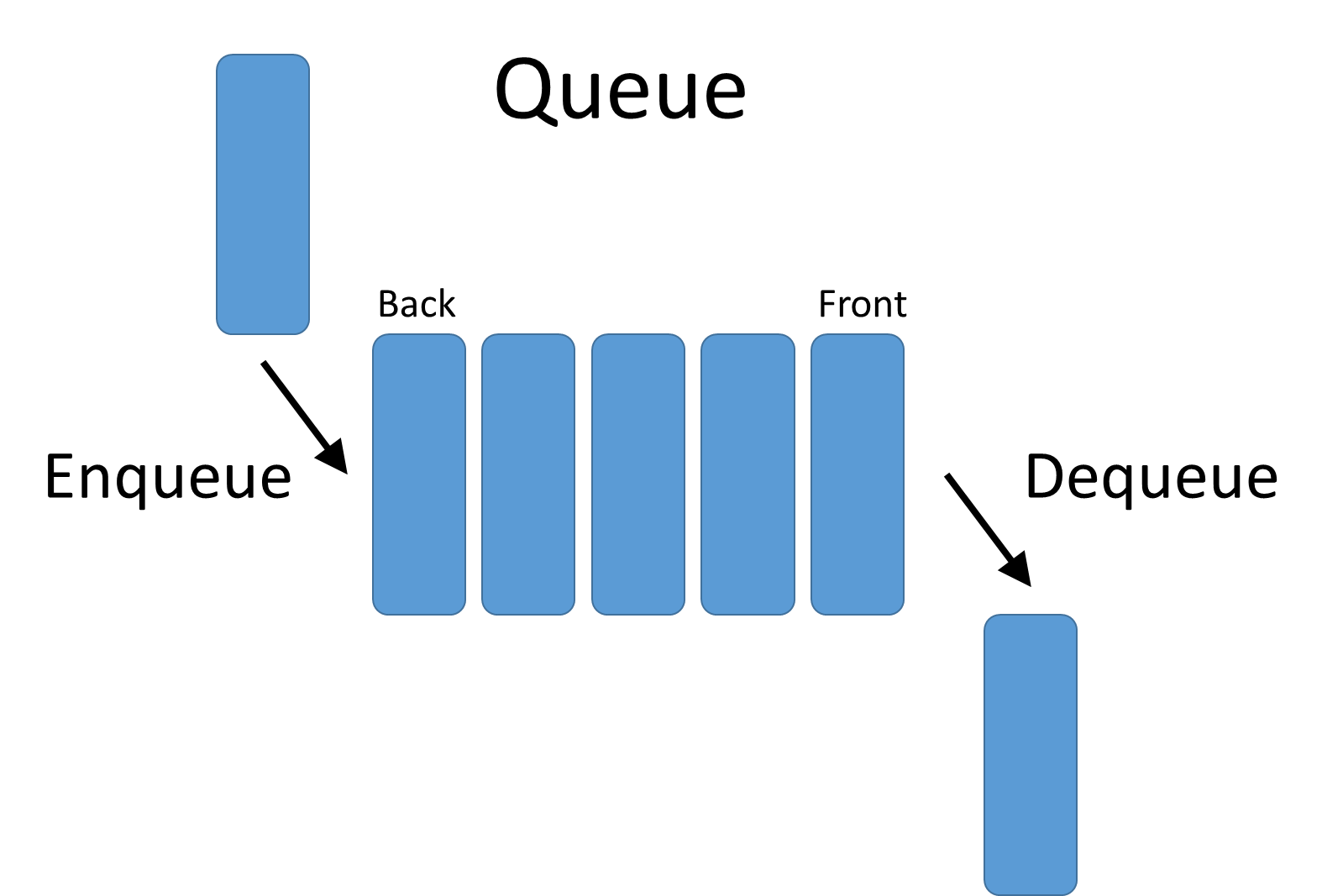
Queue is a linear data structure where the first element is inserted from one end called REAR and deleted from the other end called as FRONT. (FIFO)

| enqueue() | This function defines the operation for adding an element into queue. |
| dequeue() | This function defines the operation for removing an element from queue. |
|
Pointers |
|
| Front | Front is used to get the front data item from a queue. |
| Rear | Rear is used to get the last item from a queue. |
Queue interface
Queue uses
- Asynchronous data transfer (file IO, pipes, sockets)
- Simulation of real-world queues such as lines at a ticket counter or any other first-come first-served scenario requires a queue.
- BFS (Breadth First search) in a Graph. It is an algorithm for traversing or searching graph data structures. It starts at some arbitrary node of a graph and explores the neighbor nodes first, before moving to the next level neighbors.This Algorithm uses Queue data structure.
- Handling of interrupts in real-time systems. The interrupts are handled in the same order as they arrive, First come first served.
- Etc
Problem #4
Implement queue using linked list
Problem #5
1. Implement queue using stack API only
2. Implement stack using queue API only
Problem #6
Implement priority queue
const queue = new PriorityQueue();
queue.enqueue("one", 10);
queue.enqueue("two", 10);
queue.equeue("truee", 1);
queue.dequeue() // "three";
queue.dequeue() // "one"Thank you!

Algorithms #7
By Vladimir Vyshko
Algorithms #7
Stack vs Queue, use cases, overview
- 708



