Spectral Normalization for Generative Adversarial Networks
(SN-GAN)
ICLR 2018
Takeru Miyato, Toshiki Kataoka, Masanori Koyama, Yuichi Yoshida
Outline
- GAN
-
Wasserstein GAN (WGAN)
-
Spectral Normalization GAN (SN-GAN)
-
Experiments
-
Questions
GAN
$$\begin{aligned}\min_G\max_D\mathcal{L}&=\min_G\max_D\mathbb{E}_{x\sim p_{real}}[log(D(x))]+\mathbb{E}_{x\sim p_G}[{log(1-D(x))}]\\&=\min_G\max_D 2JS(\mathbb{P}_r|\mathbb{P}_g)+2log2\end{aligned}$$
note that
$$JS(\mathbb{P}_r|\mathbb{P}_g)=KL(\mathbb{P}_r|\frac{\mathbb{P}_r+\mathbb{P}_g}{2})+KL(\mathbb{P}_g|\frac{\mathbb{P}_r+\mathbb{P}_g}{2})$$
Unstable
Training
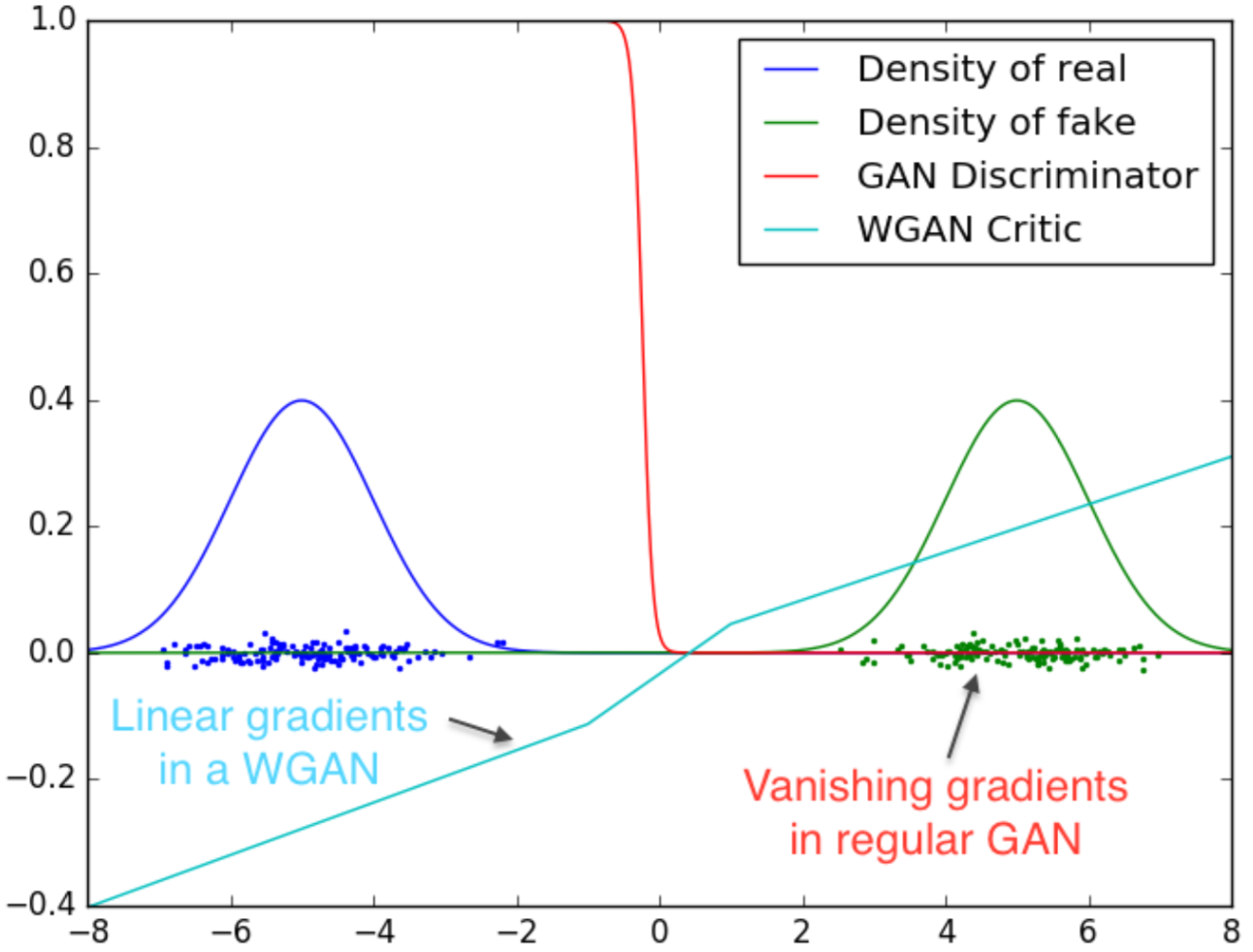
source: Arjovsky, Martin, Soumith Chintala, and Léon Bottou. "Wasserstein gan." arXiv preprint arXiv:1701.07875 (2017).
GAN
$$\begin{aligned}\min_G\max_D\mathcal{L}&=\min_G\max_D\mathbb{E}_{x\sim p_r}[log(D(x))]+\mathbb{E}_{x\sim p_g}[{log(1-D(x))}]\\&=\min_G\max_D 2JS(\mathbb{P}_r|\mathbb{P}_g)+2log2\end{aligned}$$
Why Mode collapse:
In order to avoid gradient vanish for Generator, change
$$\min_G\mathcal{L}_G=\min_G\mathbb{E}_{x\sim p_G}[{log(1-D(x))}]$$
to
$$\min_G\mathcal{L}_G=\min_G\mathbb{E}_{x\sim p_G}[-log(D(x))]$$
then
$$\mathcal{L}_G=KL(\mathbb{P}_g|\mathbb{P}_r)-2JS(\mathbb{P}_r|\mathbb{P}_g)$$
$$\rightarrow\mathbb{P}_g\text{ tends to converge to a small region}$$
Wasserstein GAN
Wasserstein Distance:
$$W(\mathbb{P}_r, \mathbb{P}_{\theta})=\inf_{\gamma\in\Pi(\mathbb{P}_r, \mathbb{P}_{\theta})}\mathbb{E}_{(x,y)\sim\gamma}[\Vert x-y\Vert]$$
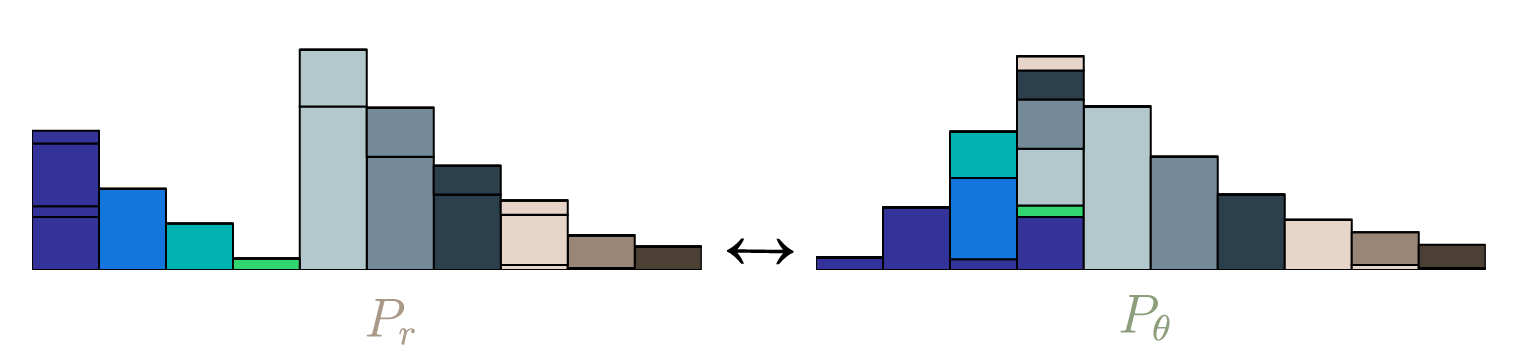
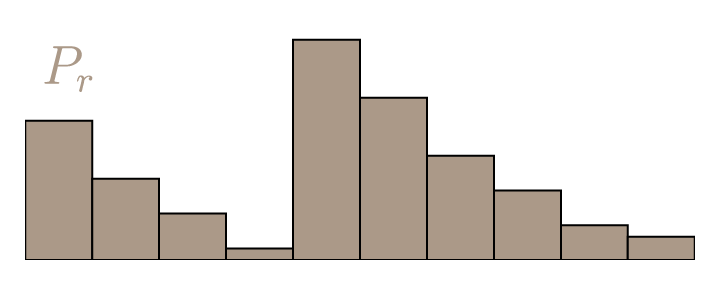
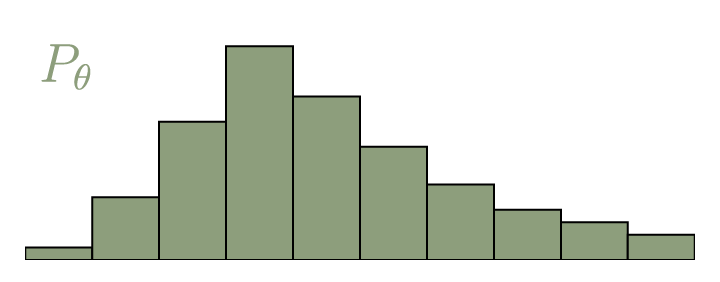
source: https://vincentherrmann.github.io/blog/wasserstein/
Wasserstein GAN
Wasserstein Distance:
$$\text{If }G\text{ is continuous in }\theta$$
$$W(\mathbb{P}_r, \mathbb{P}_{\theta})=\inf_{\gamma\in\Pi(\mathbb{P}_r, \mathbb{P}_g)}\mathbb{E}_{(x,y)\sim\gamma}[\Vert x-y\Vert]$$
- $$W(\mathbb{P}_r, \mathbb{P}_{\theta})\text{ is }\mathbf{continuous}\text{ every where.}$$
- $$W(\mathbb{P}_r, \mathbb{P}_{\theta})\text{ is }\mathbf{almost}\text{ }\mathbf{ differentiable}\text{ every where.}$$
Dual representation:
$$W(\mathbb{P}_r, \mathbb{P}_{\theta})=\sup_{\Vert f\Vert_{Lip}\le 1}\mathbb{E}_{x\sim\mathbb{P}_r}[f(x)]-\mathbb{E}_{x\sim\mathbb{P}_{\theta}}[f(x)]$$
$$\text{where the supremum is over all the 1-Lipschitz functions }f:X\rightarrow\mathbb{R}$$
Wasserstein GAN
Wasserstein distance:
$$W(\mathbb{P}_r, \mathbb{P}_{\theta})=\sup_{\Vert f\Vert_{Lip}\le 1}\mathbb{E}_{x\sim\mathbb{P}_r}[f(x)]-\mathbb{E}_{x\sim\mathbb{P}_{\theta}}[f(x)]$$
$$\text{Use Neural Network(Discriminator) to approximate }f$$
$$W(\mathbb{P}_r, \mathbb{P}_{g})=\max_D\mathbb{E}_{x\sim\mathbb{P}_r}[D(x)]-\mathbb{E}_{x\sim\mathbb{P}_{g}}[D(x)]$$
$$\text{The remaining work is to restrict the Lipschitz constant of }D$$
$$\Vert D\Vert_{Lip}\le1$$
Different Approaches
Directly restrict lipschitz constant
- WGAN [3]: Weight clipping
- WGAN-GP [5]: Gradient Penalty
$$\mathcal{L}_{GP}=\lambda(\Vert \nabla_{\hat{x}}D(\hat{x})\Vert_2-1)^2$$
- SN-GAN [6]: Spectral Normalization
For Discriminator:
$$\begin{aligned}\theta_D&\leftarrow \theta_D+\alpha\cdot \nabla_{\theta_D}\mathcal{L}_D\\\theta_D&\leftarrow clip(\theta_D,-c,c)\end{aligned}$$
$$\begin{aligned}&W^l_{SN}\leftarrow W^l/\sigma(W^l)\\&W^l\leftarrow W^l-\alpha\cdot \nabla_{W^l}\mathcal{L}(W^l_{SN},D)\\&\sigma(\cdot)\text { spectral norm}\end{aligned}$$
Indirect approaches
- BEGAN [4]: Maximize the lower bound of Wasserstein Loss
SN GAN
- Spectral Normalization:
$$\begin{aligned}&W^l_{SN}=W^l/\sigma(W^l)\\&\sigma(\cdot)\text { denotes spectral norm, maximum singluar value}\end{aligned}$$
- Apply Spectral Normalization on each layer of D(x) then:
$$\Vert D_{\theta}\Vert _{Lip}\le1$$
- proof:
$$\begin{aligned}\text{Let }D(x)=&a_L(W^L(a_{L-1}(W^{L-1}(\cdots a^1(W^1 x)\cdots))))\\\Vert D(x)\Vert_{Lip}\le&\Vert a_L\Vert_{Lip}\cdot\Vert W^L\Vert_{Lip}\cdot\Vert a_{L-1}\Vert_{Lip}\cdot\Vert W^{L-1}\Vert_{Lip}\\&\cdots\Vert a_1\Vert_{Lip}\cdot\Vert W^1\Vert_{Lip}\\ \sigma(W^l_{SN})=&\sigma(W^l/\sigma(W^l))=1\end{aligned}$$
SN GAN

Experiments
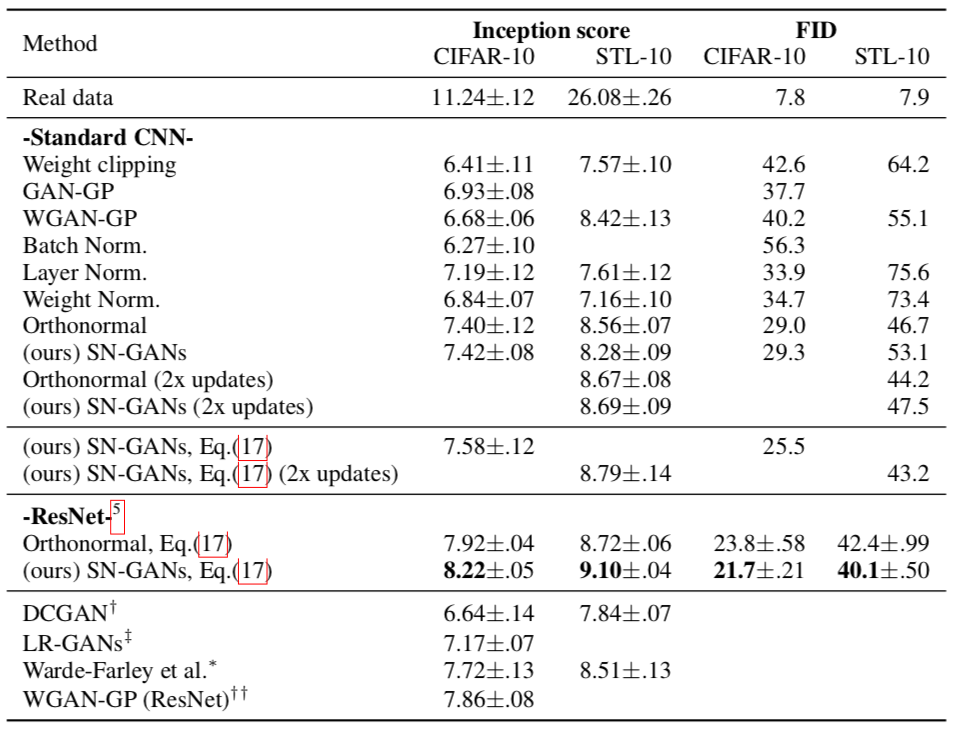
Experiments
$$\begin{aligned}\beta_1,\beta_2:&\text{ parameter for Adam}\\\alpha:&\text{ learning rate}\\n_{dis}:&\text{ the number of updates of}\\&\text{ the discriminator per one update}\\&\text{ of the generator and}\end{aligned}$$
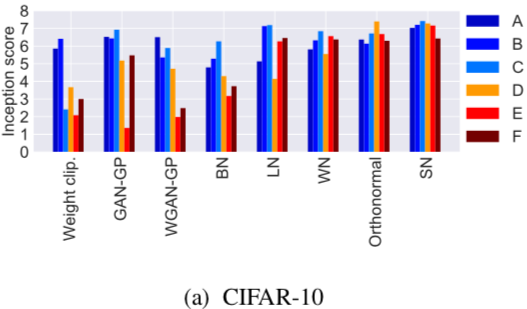
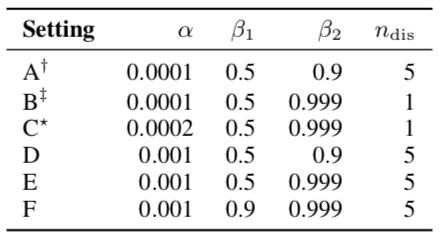
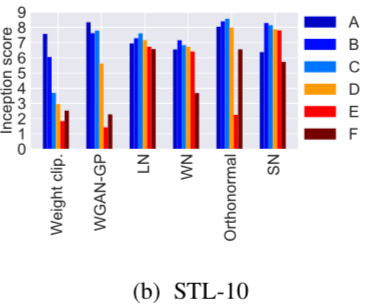
Experiments
| Mode Name | Loss | Architecture | Does it work? |
|---|---|---|---|
| DCGAN (in paper) * | KL | TransConv | work |
| WGAN (in paper) | Wasserstein | TransConv | work |
| WGAN-GP * | Wasserstein | TransConv | work |
| WGAN-GP (in paper) * | Wasserstein | ResNet | work |
| SN-GAN * | Wasserstein | TransConv | work |
| SN-GAN (in paper) * | Hinge loss | ResNet | work |
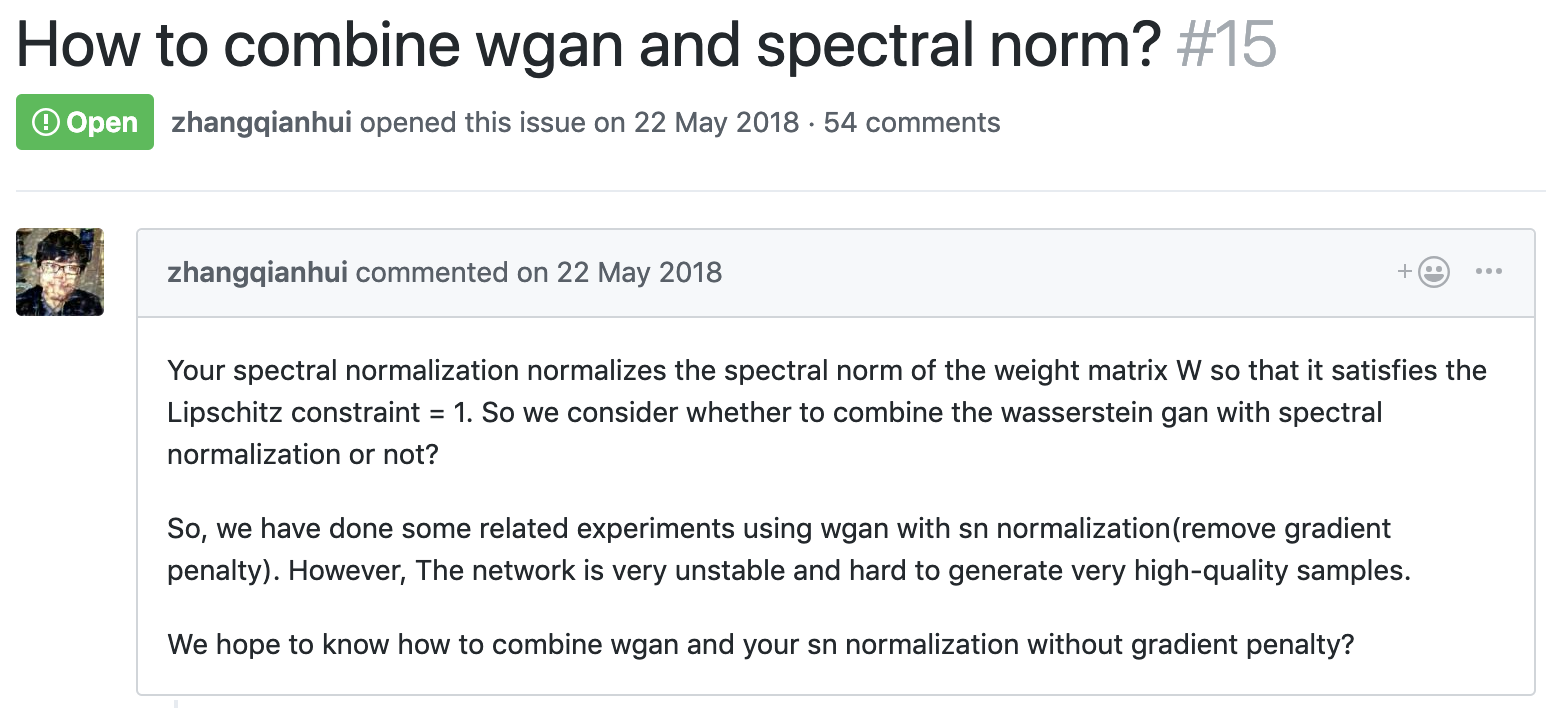
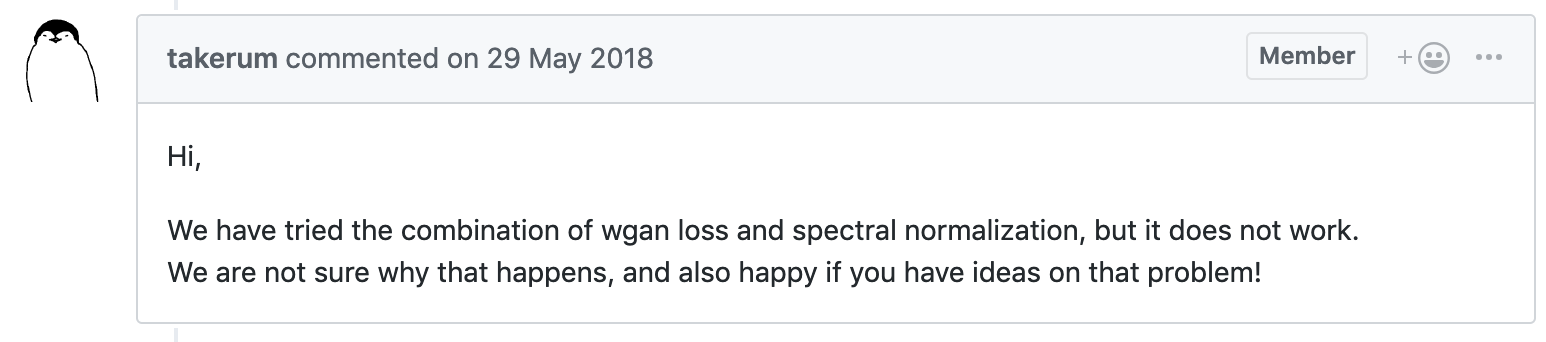
| SN-GAN * | Wasserstein | ResNet | NOT WORK |
Experiments
* Means I have tested.
source: github
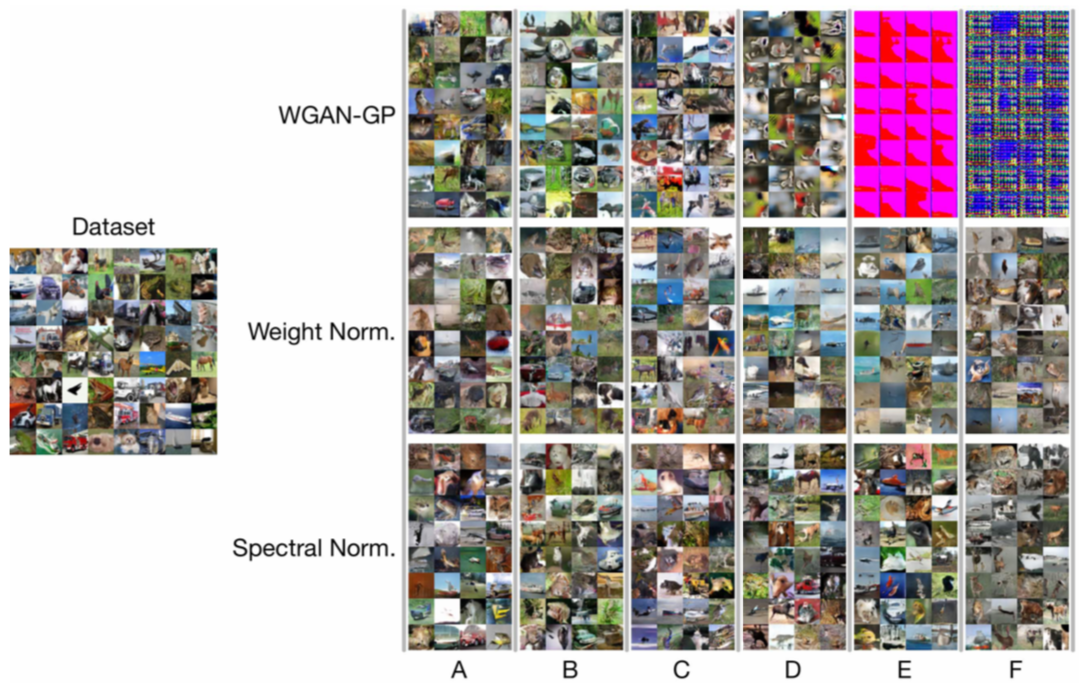
SN-GAN
(Hinge loss + ResNet)



SN-GAN
(W. dis. + ResNet)
SN-GAN
(W. dis. + TransConv)
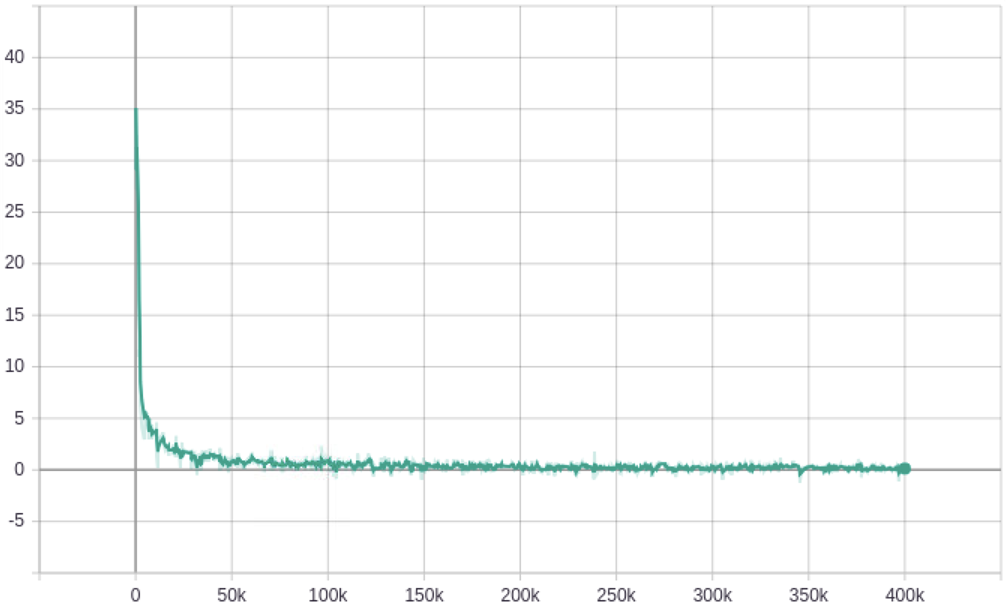
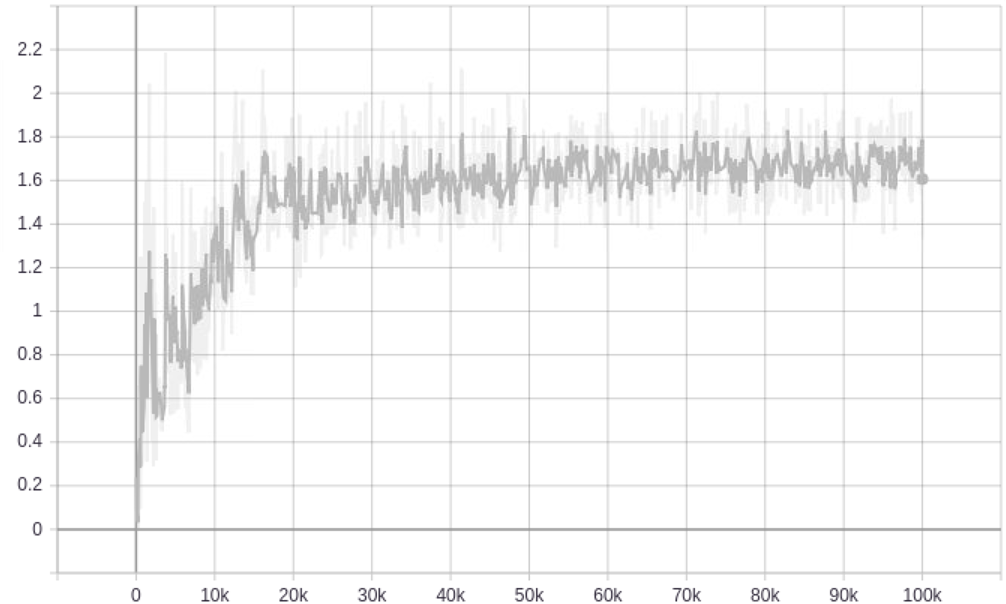
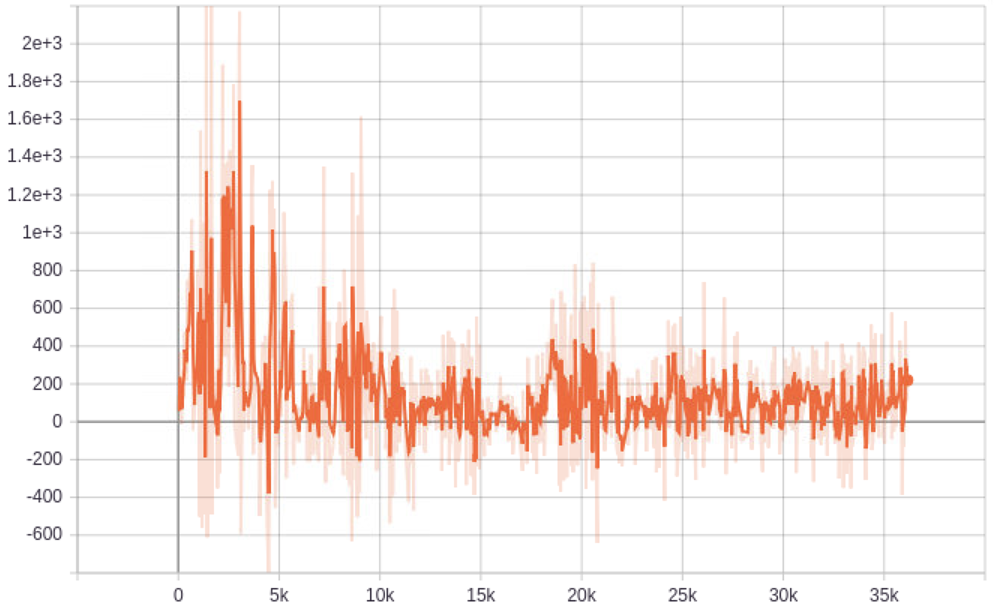

1.8
0.25
References
- Goodfellow, Ian, et al. "Generative adversarial nets." Advances in neural information processing systems. 2014.
- Martin Arjovsky, Léon Bottou. "Towards Principled Methods for Training Generative Adversarial Networks." International Conference on Learning Representations. 2017.
- Arjovsky, Martin, Soumith Chintala, and Léon Bottou. "Wasserstein generative adversarial networks." International Conference on Machine Learning. 2017.
- Berthelot, David, Thomas Schumm, and Luke Metz. "Began: Boundary equilibrium generative adversarial networks." arXiv preprint arXiv:1703.10717 (2017).
- Gulrajani, Ishaan, et al. "Improved training of wasserstein gans." Advances in Neural Information Processing Systems. 2017.
- Miyato, Takeru, et al. "Spectral normalization for generative adversarial networks." arXiv preprint arXiv:1802.05957 (2018).
Questions
- Why the training time of SN-GAN is less than WGAN-GP ?
- If mode collapse occurred, what is the feature of generated image
Spectral Normalization for Generative Adversarial Networks
By w86763777
Spectral Normalization for Generative Adversarial Networks
Group meeting
- 1,271



