Generative Adversarial Networks (GANs)
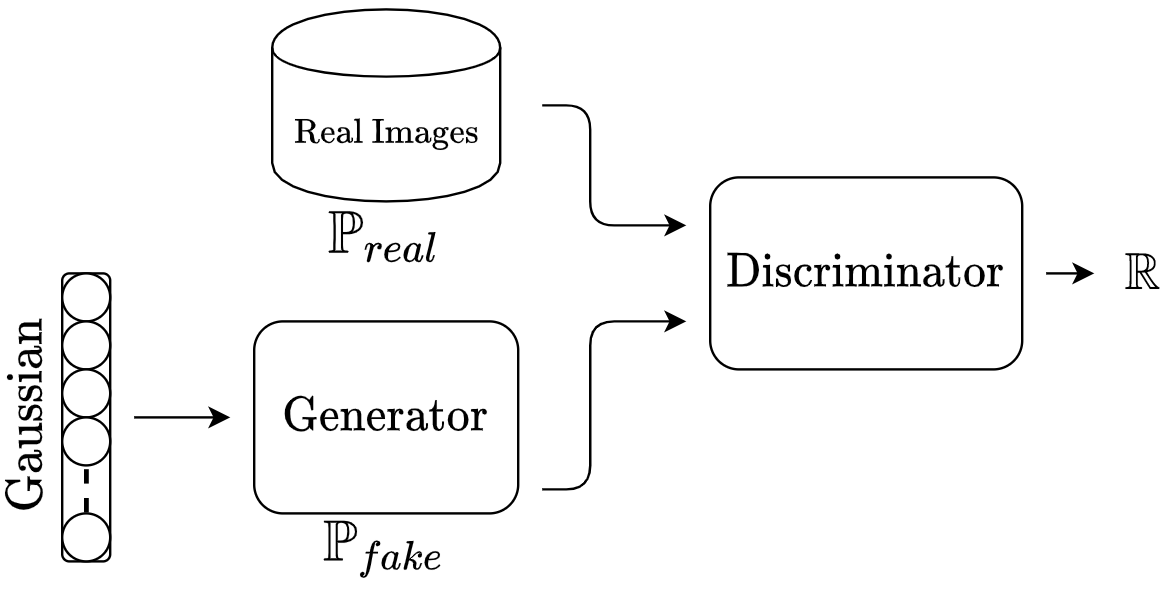
Formulation
\begin{aligned}
&G(\cdot,\theta_G):\mathbb{R}^z\rightarrow\mathcal{X}\subseteq\mathbb{R}^n\\
&D(\cdot,\theta_D):\mathcal{X}\rightarrow\mathbb{R}\\
&\text{Alternatively optimize } \theta_G,\theta_D\\
&\hat\theta_D=\arg\max_{\theta_D}\mathbb{E}_{x\sim \mathbb{P}_{real}}\big[log(D(x,\theta_D))\big]+\mathbb{E}_{x\sim \mathbb{P}_{fake}}\big[log(1-D(x,\theta_D))\big]\\
&\hat\theta_G=\arg\max_{\theta_G}\mathbb{E}_{x\sim \mathbb{P}_{fake}}\big[log(D(x,\hat\theta_D))\big]
\end{aligned}
Spectral Normalized GANs
$$\text{Let Discriminator }D(\cdot,\theta_D):\mathbb{R}^n\rightarrow\mathbb{R}\text{ be a L-layer network}$$
\begin{aligned}
&D(x,\theta_D)=W_L\bigg(\phi_{L-1}\Big(W_{L-1}\big(\cdots \phi_1(W_1 x)\big)\Big)\bigg)\\
&W_k\in\mathbb{R}^{h_k\times h_{k-1}},\forall k\in[1\cdots L-1],h_0=n,h_L=1\\
&\phi_k\in\{\text{ReLU},\text{ LeakyReLU}\},\forall k\in[1\cdots L-1]
\end{aligned}
$$\text{Normalize each layer by spectral norm}$$
\begin{aligned}
&\bar{W_k}=W_k/\sigma(W_k)\\
&\bar{D}(x,\theta_D)=\bar{W}_L\bigg(\phi_{L-1}\Big(\bar{W}_{L-1}\big(\cdots \phi_1(\bar{W}_1 x)\big)\Big)\bigg)\\
\end{aligned}
Spectral Normalized GANs
$$\text{Normalize each layer by spectral norm}$$
\begin{aligned}
&\bar{W_k}=W_k/\sigma(W_k)\Rightarrow\sigma(\bar{W_k})=\Vert W_k\Vert_{Lip}=1\\
&\bar{D}(x,\theta_D)=\bar{W}_L\bigg(\phi_{L-1}\Big(\bar{W}_{L-1}\big(\cdots \phi_1(\bar{W}_1 x)\big)\Big)\bigg)\\
&\Rightarrow\Vert \bar{D}(\cdot,\theta_D)\Vert_{Lip}\le 1
\end{aligned}
$$\text{ReLU}$$
$$\text{LeakyReLU}$$
y=
\begin{dcases}
x,& \text{if } x\geq 1\\
0,& \text{otherwise}
\end{dcases}
y=
\begin{dcases}
x,& \text{if } x\geq 1\\
\alpha x,& \text{otherwise}
\end{dcases}
Spectral Normalized GANs
\begin{aligned}
\Vert \bar{D}(\cdot,\theta_D)\Vert_{Lip}\le 1
\end{aligned}
\begin{aligned}
&\text{Conclusion:}\\
&\text{Finite Lipschitz constant is the most important characteristic}\\
&\text{for Discriminator}\\
\end{aligned}
\Vert W_k\Vert_{Lip}=k\Leftrightarrow\frac{\Vert W_kx-Wk_y\Vert}{\Vert x-y\Vert}\le k,\forall x,y\in\mathcal{X}
Gradient Normalized GANs
\begin{aligned}
&\text{Suppose Discriminator }f:\mathcal{X}\subseteq\mathbb{R}^n\rightarrow\mathbb{R}\text{ is continuously differentiable,}\\
&\text{then}\\
\end{aligned}
\Vert f\Vert_{Lip}=1\Leftrightarrow\Vert\nabla f\Vert\le 1
\begin{aligned}
\Vert f(x)-f(y)\Vert&=\Big\Vert\int_y^x\nabla f(r)\cdot dr\Big\Vert\\
&=\Big\Vert\int_0^1\langle \nabla f(x\cdot t+y\cdot(1-t)),x-y\rangle dt\Big\Vert\\
&\le\Big\Vert\int_0^1\Vert \nabla f(x\cdot t+y\cdot(1-t))\Vert\cdot\Vert x-y\Vert\cdot dt\Big\Vert\\
&\le\Big\Vert\int_0^1\Vert x-y\Vert\cdot dt\Big\Vert\\
&=\Vert x-y\Vert
\end{aligned}
\begin{aligned}
&\text{Proof: }(\Leftarrow)\\
&f\text{ is continuously differentiable}\\
&\Rightarrow\nabla f\text{ is a conservative vector field}\\
&\Rightarrow\text{Path independence of the line integral}
\end{aligned}
Gradient Normalized GANs
\begin{aligned}
&\text{Define Gradient Normalized Discriminator }\bar{f}=\frac{f}{\Vert\nabla f\Vert_2},\\
&\text{and let}
\end{aligned}
f(x)=W_L\bigg(\phi_{L-1}\Big(W_{L-1}\big(\cdots \phi_1(W_1 x)\big)\Big)\bigg)
\begin{aligned}
&\text{Suppose }\phi_k\in\{\text{ReLU, LeakyReLU}\},\forall k\in[1\cdots L-1]\text{, then}
\end{aligned}
\begin{aligned}
&\nabla^2 f=\mathbb{0}\\
&\Rightarrow\Vert\nabla \bar{f}\Vert=\Big\Vert\frac{\nabla f\Vert\nabla f\Vert-f\frac{\nabla^2f\nabla f}{\Vert\nabla f\Vert}}{\Vert\nabla f\Vert^2}\Big\Vert=1\\
\end{aligned}
\begin{aligned}
&\text{for most of points in }\mathcal{X}.\\
&\text{However}
\end{aligned}
\nRightarrow\Vert\bar{f}\Vert_{Lip}=1
Generative Adversarial Networks
By w86763777
Generative Adversarial Networks
- 312



