Amazon CoRo February Update

Feb 27, 2025

Adam Wei

Agenda

  1. Recap
  2. Sim-Sim Setup
  3. Sim-Sim Experiments
  4. Paper plan (IROS)

Question

Would you prefer the monthly check-ins to be presentation-oriented or discussion-oriented?

Robot Data Diet

Big data

Big transfer gap

Small data

No transfer gap

Ego-Exo

 robot teleop

Open-X

simulation

How can we obtain data for imitation learning?

Cotrain from different data sources

(ex. sim & real)

Problem Formulation

\mathcal{D}_{R}\sim p_{R}(O,A)
\mathcal{D}_S\sim p_{S}(O,A)

Cotraining: Use both datasets to train a model that maximizes some test objective

Model: Diffusion Policy

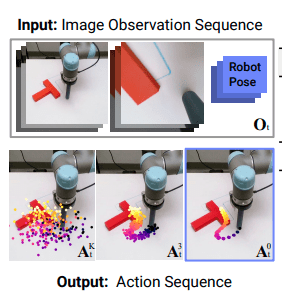
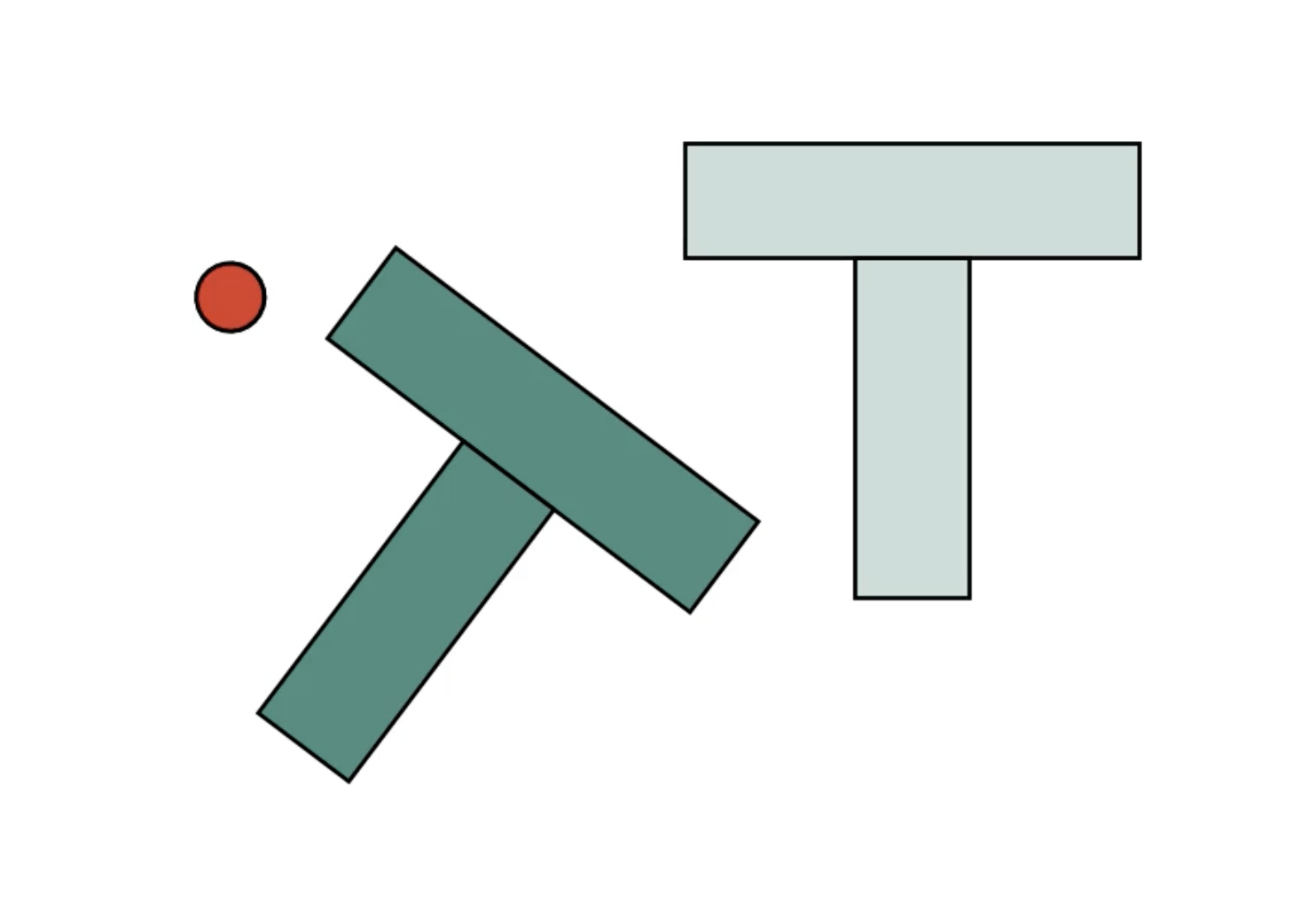
Test objective: Success rate on a planar pushing task

Vanilla Cotraining

\mathcal L_{\mathcal D^\alpha} = \alpha \textcolor{red}{\mathcal L_{\mathcal D_R}} + (1-\alpha) \textcolor{blue}{\mathcal L_{\mathcal D_S}}

(Tower property of expectations)

Vanilla Cotraining:

  1. Choose \(\alpha \in [0,1]\)
  2. Train a diffusion policy that minimizes \(\mathcal L_{\mathcal D^\alpha}\)

\(\mathcal D^\alpha\)          Dataset mixture

  • Sample from \(\mathcal D_R\) w.p. \(\alpha\)
  • Sample from \(\mathcal D_S\) w.p, \(1-\alpha\)

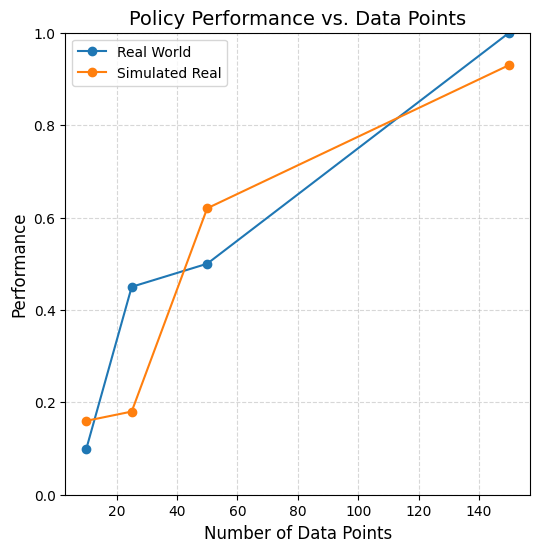
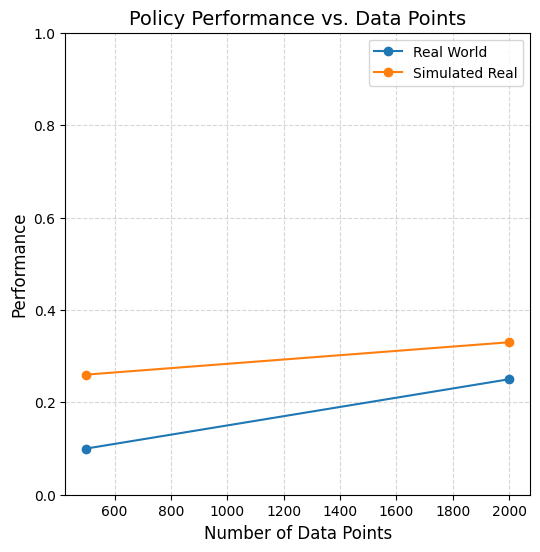
Results

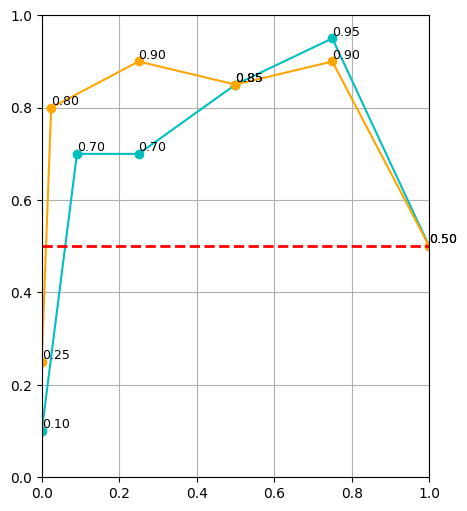
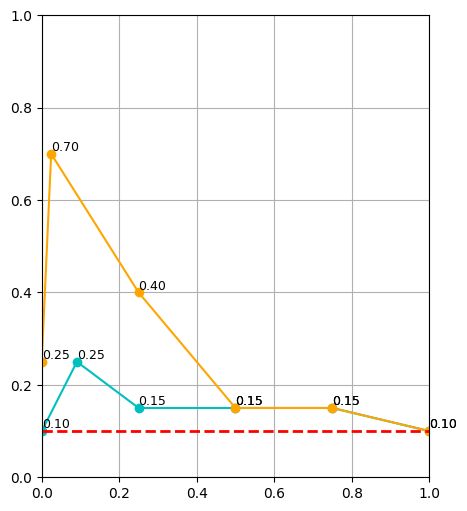
\(|\mathcal D_R| = 10\)

\(|\mathcal D_R| = 50\)

\(|\mathcal D_R| = 150\)

cyan: \(|\mathcal D_S| = 500\)     orange: \(|\mathcal D_S| = 2000\)     red: real only

Highlights

 10 real demos

2000 sim demos

 50 real demos

500 sim demos

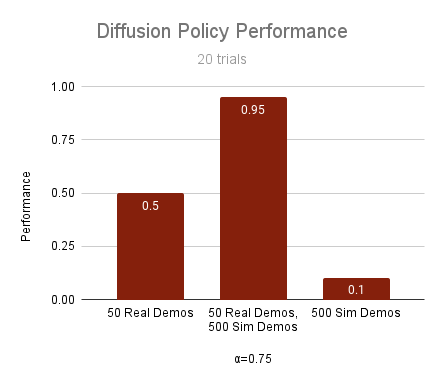
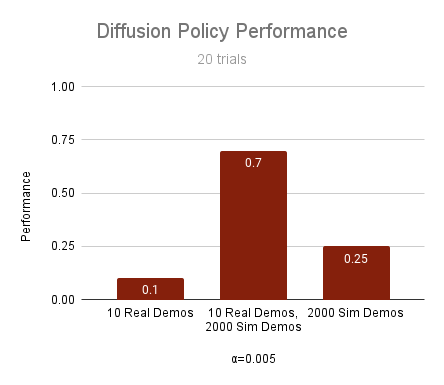
  • Cotraining can drastically improve performance

Key Takeaways

  1. Policy's are sensitive to \(\alpha\), especially when \(|\mathcal D_R|\) is small
  2. Smaller \(|\mathcal D_R|\) → smaller \(\alpha\), larger \(|\mathcal D_R|\) → larger \(\alpha\)
  3. Scaling \(|\mathcal D_S|\) improves performance.
  4. Scaling \(|\mathcal D_S|\) reduces sensitivity of \(\alpha\)

Initial experiments suggest that scaling up sim is a good idea!

... to be verified at larger scales with sim-sim experiments

Sim2Sim Setup

Can we create 2 different simulation environments that replicate the sim2real gap?

  • i.e. sim2sim gap \(\approx\) sim2real gap

If yes, need to emulate...

  1. Sim2real visual gap
  2. Sim2real physics gap

Sim2Sim Visual Gap

Sim2Real

Sim2Sim

Simulation

"Real World"

Sim2Sim Visual Gap

Sim2Real

Sim2Sim

Simulation

"Real World"

Quasi-static dynamics

Quasi-static dynamics

Hydroelastic + Drake Physics

Real World Physics

Sim2Real vs Sim2Sim

Real Data Policies

Sim Data Only

Pros & Cons of Sim2Sim

Cons

  • Only a proxy for sim-and-real results
  • Hard to perfectly emulate the sim2real gap

Pros

  • Automated, high confidence policy evaluation + logs
  • Large-scale experiments
  • Precise control of the magnitude of the sim2real gaps
    • Important for distribution shift experiments
  • Informative for sim-and-real

Sim2Sim Experiments

  1. Distribution Shifts
  2. Isolating the effect of physics vs visual shifts
  3. The role of sim2real in cotraining
  4. Asymptotes of cotraining (mini-scaling laws)

Distribution Shifts

Setting up a simulator for data generation is non-trivial

  • camera calibration, colors, assets, physics, tuning, data filtering, task-specifications, etc

+ Actions

What qualities matter in the simulated data?

Distribution Shifts

Domain Rand.

Color Shift

Physics Shift

(CoM y-offset)

Level 1

Level 2

Level 3

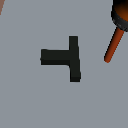
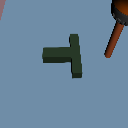
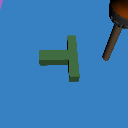
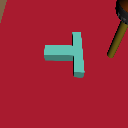
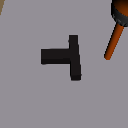
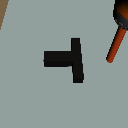
+3cm

-3cm

-6cm

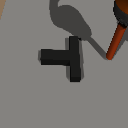
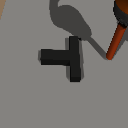
Level 4

Level 0

Drake physics

Visual Shifts

Distribution Shifts

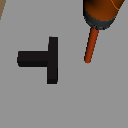
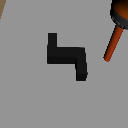
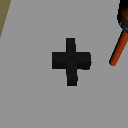
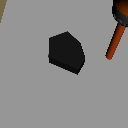
Goal Shift

Object Shift

Task Shift

Level 1

Level 2

Level 3

Only 1 level

Level 0

Distribution Shifts

Experimental Setup

  • Tested ~3 levels of shift for each shift**
  • \(|\mathcal D_R|\) = 50, \(|\mathcal D_S|\) = 2000, 
  • \(\alpha = 0,\ \frac{|\mathcal{D}_{R}|}{|\mathcal{D}_{R}|+|\mathcal{D}_{S}|},\ 0.25,\ 0.5,\ 0.75,\ 0.9,\ 0.95,\ 1\)

** Except object shift

Results

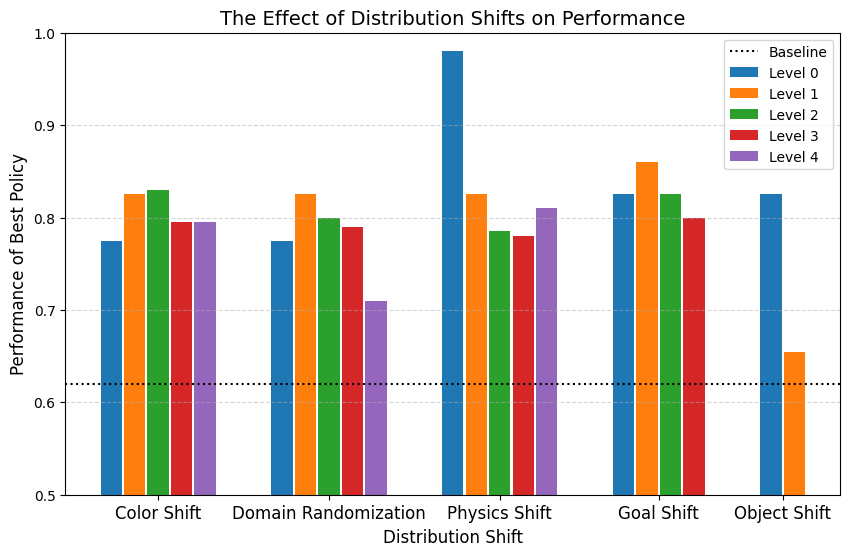
Results

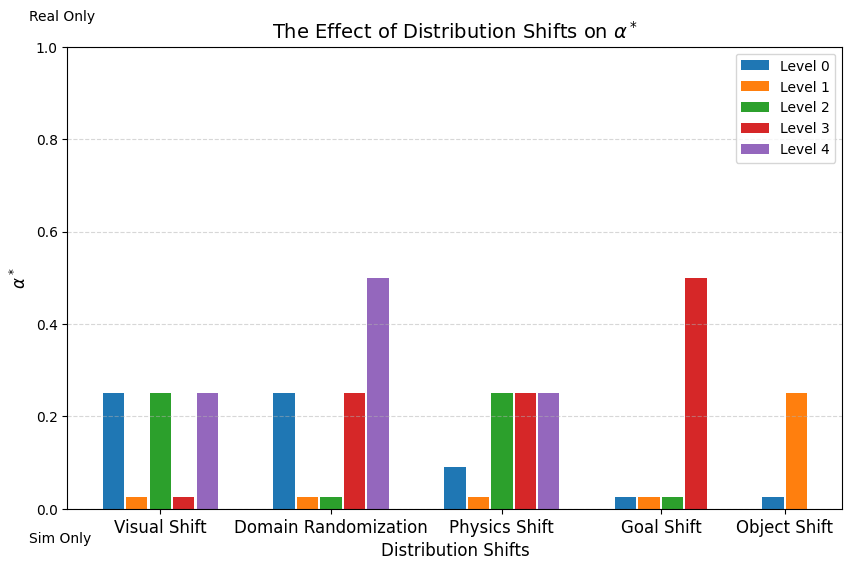
Conclusions

  1. Smaller physics shift \(\implies\) better performance
  2. Some visual shift is desired, but performance degrades with large visual shifts
  • Required to distinguish sim and real
  • Visual encoders learn robust representations

3.  Task shift (??)  TBD

Sim2Sim Experiments

  1. Distribution Shifts
  2. Isolating the effect of physics vs visual shifts
  3. The role of sim2real in cotraining
  4. Asymptotes of cotraining (mini-scaling laws)

Removing Physics/Visual Gap

In sim2sim, we can analyze different types of sim2real gaps independently.

Physics Gap

Visual Gap

Off

On

Off

On

Perfect Simulator

Perfect Physics Engine

Perfect Renderer

Regular Cotraining

Results: \(|\mathcal D_R|=50\), \(|\mathcal D_S|=500\)

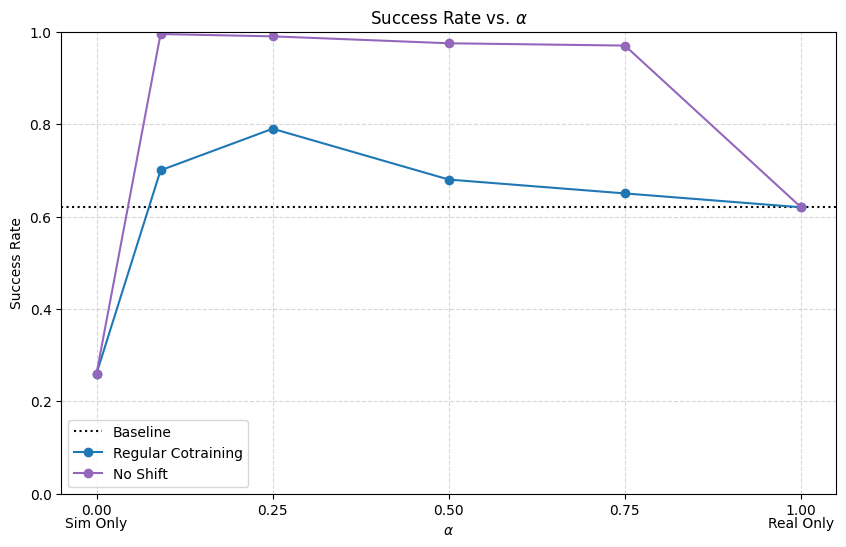
Results: \(|\mathcal D_R|=50\), \(|\mathcal D_S|=500\)

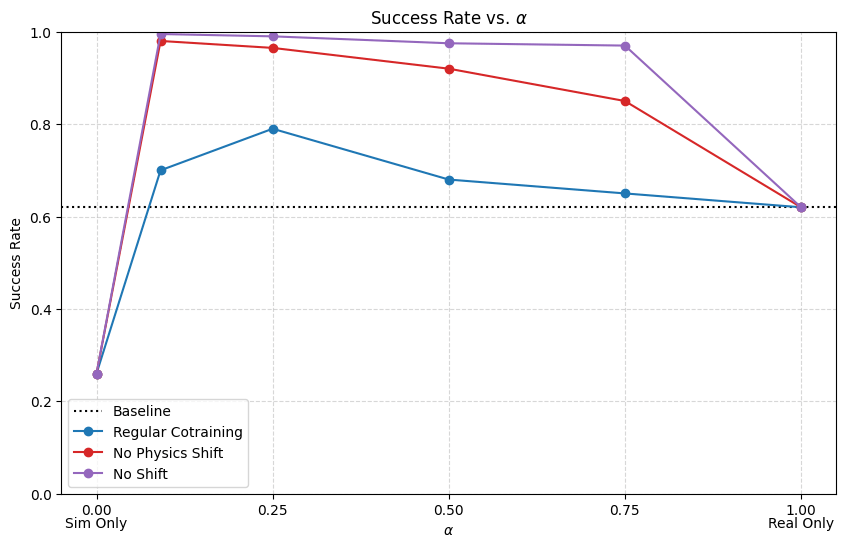
Results: \(|\mathcal D_R|=50\), \(|\mathcal D_S|=500\)

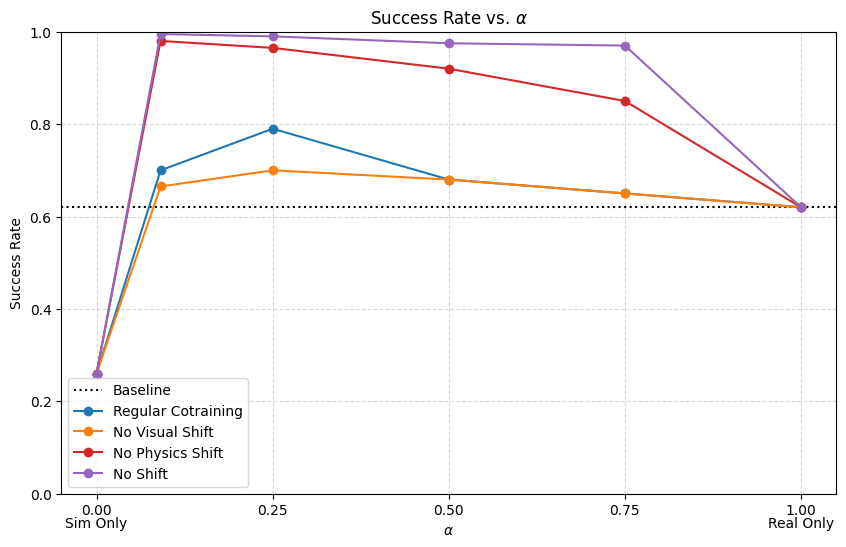
Results: \(|\mathcal D_R|=50\), \(|\mathcal D_S|=500\)

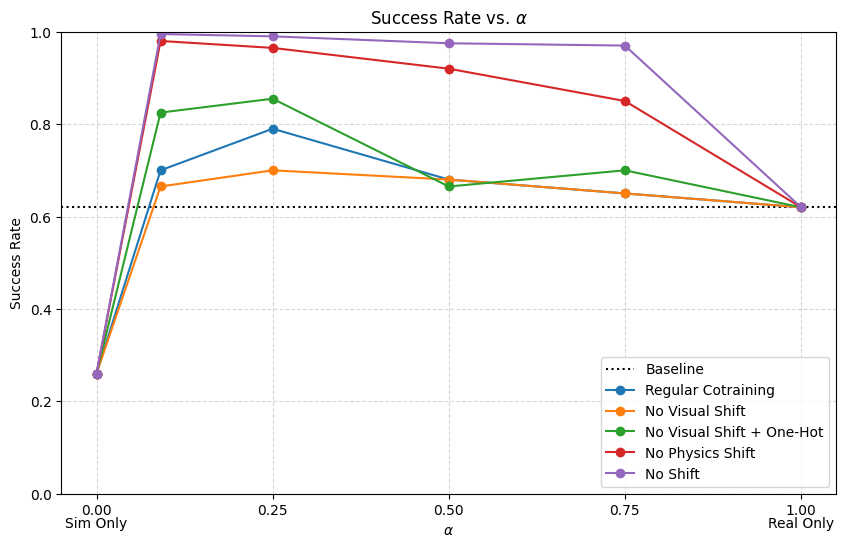
Results: \(|\mathcal D_R|=50\), \(|\mathcal D_S|=500\)

Conclusions

  1. Visual encoders are robust to visual gaps
  2. Reducing physics gap is very important for dynamic or contact-rich tasks
  3. If there is physics gap, the model needs to have enough information in its inputs to distinguish sim and real​​
  • Visual gap or one-hot encoding
  • Some visual gap is not detrimental; in fact helpful

Sim2Sim Experiments

  1. Distribution Shifts
  2. Isolating the effect of physics vs visual shifts
  3. The role of sim2real in cotraining
  4. Asymptotes of cotraining (mini-scaling laws)

Sim2Sim Experiments

  1. Distribution Shifts
  2. Isolating the effect of physics vs visual shifts
  3. The role of sim2real in cotraining
  4. Asymptotes of cotraining (mini-scaling laws)

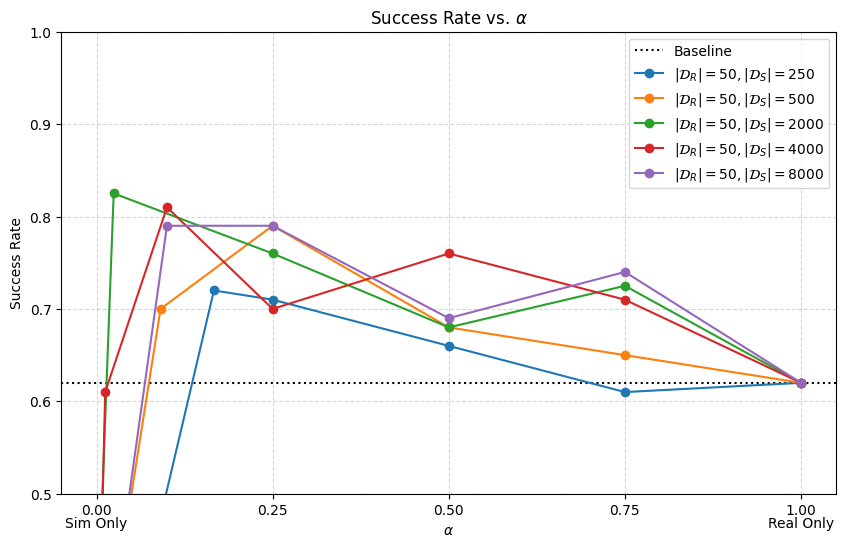
Cotraining (Mini) Scaling Laws

  1. Policy's are sensitive to \(\alpha\), especially when \(|\mathcal D_R|\) is small
  2. Smaller \(|\mathcal D_R|\) → smaller \(\alpha\), larger \(|\mathcal D_R|\) → larger \(\alpha\)
  3. Scaling \(|\mathcal D_S|\) improves performance.
  4. Scaling \(|\mathcal D_S|\) reduces sensitivity of \(\alpha\)

Initial experiments suggest that scaling up sim is a good idea!

... to be verified at larger scales with sim-sim experiments

Cotraining (Mini) Scaling Laws

Disclaimer: Preliminary Results

  • Sim2sim gap was too small (relative to sim2real gap)
  • Re-doing these experiments with larger sim2sim gap

Results

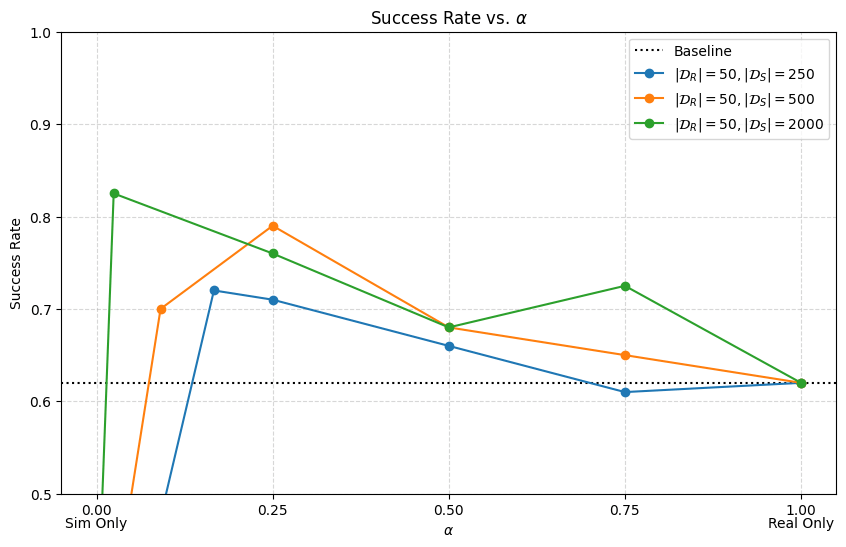
Results

Plan For IROS

Section 1: Real World Experiments

  • Cotraining results, trends, finetuning comparison

Section 2: Simulation Experiments

  • Distribution shifts, isolating sim2real gaps, scaling up Section 1 experiments

Section 3: Empirical Analysis

  • Sim-and-real discernability + positive transfer, the role of sim2real, cotraining as regularization

Misc. Slides

Cotrained Policies

Cotrained policies exhibit similar characteristics to the real-world expert regardless of the mixing ratio

Real Data

  • Aligns orientation, then translation sequentially
  • Sliding contacts
  • Leverage "nook" of T

Sim Data

  • Aligns orientation and translation simultaneously
  • Sticking contacts
  • Pushes on the sides of T

How does cotraining improve performance?

Hypothesis

  1. Cotrained policies can identify the sim vs real: sim data helps by learning better representations and filling in gaps in real data
  2. Sim data prevents overfitting and acts as a regularizor
  3. Sim data provides more information about high probability unconditional actions \(p_A(a)\)

Probably some combination of the above.

Hypothesis 1: Binary classification

Cotrained policies can identify the sim vs real: sim data improves representation learning and fills in gaps in real data

Policy Observation embeddings acc. Final activation acc.
50/500, alpha = 0.75 100% 74.2%
50/2000, alpha = 0.75 100% 89%
10/2000, alpha = 0.75 100% 93%
10/2000, alpha = 5e-3 100% 94%
10/500, alpha = 0.02 100% 88%

Only a small amount of real data is needed to separate the embeddings and activations

Hypothesis 1: tSNE

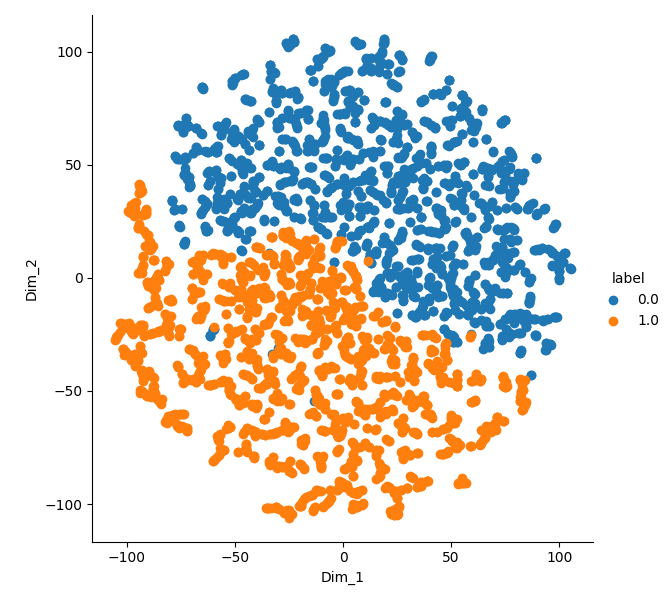
  • t-SNE visualization of the observation embeddings

Hypothesis 1: kNN on actions

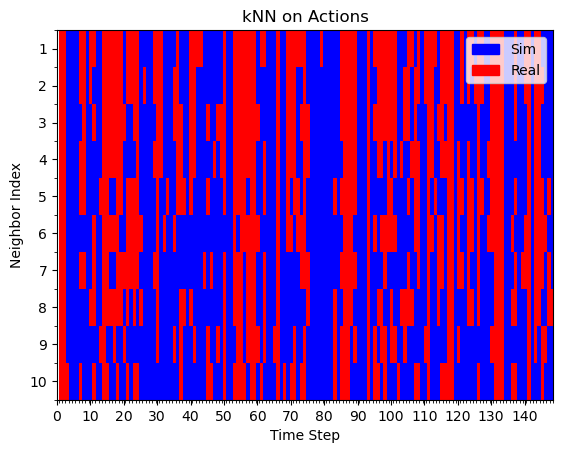
Real Rollout

Sim Rollout

Mostly red with blue interleaved

Mostly blue

Assumption: if kNN are real/sim, this behavior was learned from real/sim

Similar results for kNN on embeddings

Hypothesis 2

Sim data prevents overfitting and acts as a regularizor

\begin{aligned} \mathcal{L_{train}}=\textcolor{red}{\mathcal{L}_{objective}} + \lambda\textcolor{blue}{\mathcal{L}_{regularizer}} \end{aligned}
\mathcal L_{\mathcal D^\alpha} = \alpha \textcolor{red}{\mathcal L_{\mathcal D_R}} + (1-\alpha) \textcolor{blue}{\mathcal L_{\mathcal D_S}}

When \(|\mathcal D_R|\) is small, \(\mathcal L_{\mathcal D_R}\not\approx\mathcal L\).

\(\mathcal D_S\) helps regularize and prevent overfitting

Hypothesis 3

Sim data provides more information about \(p_A(a)\)

  • i.e. improves the cotrained policies prior on "likely actions"

Can we test/leverage this hypothesis with classifier-free guidance?

... more on this later if time allows

Hypothesis

Research Questions

  1. How can we test these hypothesis?
  2. Can the underlying principles of cotraining help inform novel cotraining algorithms?

Hypothesis

Hypothesis

  1. Cotrained policies can identify the sim vs real: sim data helps by learning better representations and filling in gaps in real data
  2. Sim data prevents overfitting and acts as a regularizor
  3. Sim data provides more information about high probability actions \(p_A(a)\)

Example ideas:

  • Hypothesis 1 \(\implies\) adversarial formulations for cotraining, digitial twins, representation learning, etc
  • Hypothesis 3 \(\implies\) classifier-free guidance, etc

Research Questions

  1. For vanilla cotraining: how do \(|\mathcal D_R|\), \(|\mathcal D_S|\), and \(\alpha\) affect the policy's success rate?
  2. How do distribution shifts affect cotraining?
  3. Propose new algorithms for cotraining
    1. Adversarial formulation
    2. Classifier-free guidance

Sim2Real Gap

Thought experiment: what if sim and real were nearly indistinguishable?

  1. Less sensitive to \(\alpha\)
  2. Each sim data point better approximates the true denoising objective
  3. Improved cotraining bounds

Sim2Real Gap

Fact: cotrained models can distinguish sim & real

Thought experiment: what if sim and real were nearly indistinguishable?

Sim2Real Gap

\mathrm{prob\ of\ error} \leq \mathrm{bound}(\alpha,|\mathcal D_R|, |\mathcal D_S|, \mathrm{dist}(\mathcal D_R,\mathcal D_S), ...)

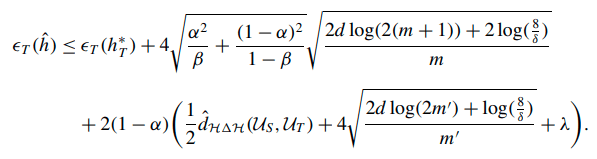
\(\mathrm{dist}(\mathcal D_R,\mathcal D_S)\) small \(\implies p^{real}_{(O,A)} \approx p^{sim}_{(O,A)} \implies p^{real}_O \approx p^{sim}_O\)

'visual sim2real gap'

Sim2Real Gap

Current approaches to sim2real: make sim and real visually indistinguishable

  • Gaussian splatting, blender renderings, real2sim, etc

\(p^{R}_O \approx p^{S}_O\)

Do we really need this? 

\(p^{R}_O \approx p^{S}_O\)

Sim2Real Gap

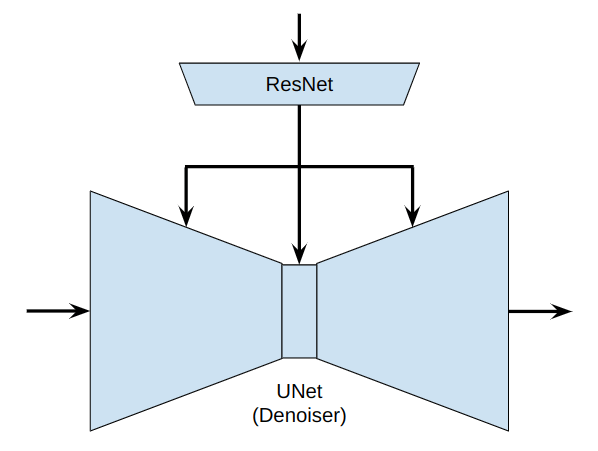
\(a^k\)

\(\hat \epsilon^k\)

\(o \sim p_O\)

\(o^{emb} = f_\psi(o)\)

\(p^{R}_O \approx p^{S}_O\)

\(p^{R}_{emb} \approx p^{S}_{emb}\)

\(\implies\)

Weaker requirement

Adversarial Objective

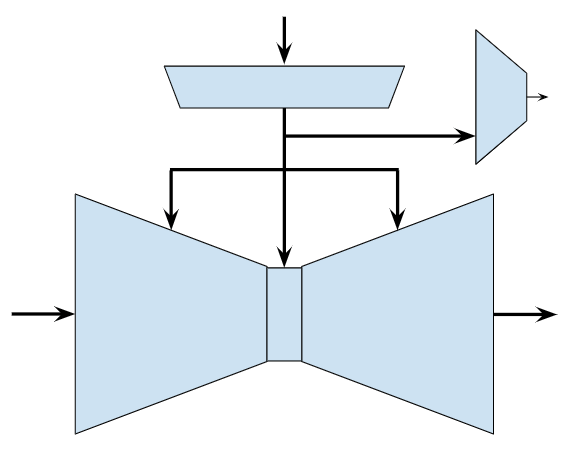
\(\epsilon_\theta\)

\(f_\psi\)

\(d_\phi\)

\(\hat{\mathbb P}(f_\psi(o)\ \mathrm{is\ sim})\)

\(\epsilon^k\)

\(a^k\)

o

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \max_\phi \mathbb E_{p^S_O}[\log d_\phi (f_\psi(o))] + \mathbb E_{p^R_O} [1-\log d_\phi (f_\psi(o))]

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \max_\phi \mathbb E_{p^S_O}[\log d_\phi (f_\psi(o))] + \mathbb E_{p^R_O} [1-\log d_\phi (f_\psi(o))]

Denoiser Loss

Negative BCE Loss

\(\iff\)

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

(Variational characterization of f-divergences)

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

Common features (sim & real)

  1. End effector position
  2. Object keypoints
  3. Contact events

Distinguishable features*

  1. Shadows, colors, textures, etc

Relavent for control...

  • Adversarial objective discourages the embeddings from encoding distinguishable features*

* also known as protected variables in AI fairness literature

Adversarial Objective

\(\epsilon_\theta\)

\(f_\psi\)

\(d_\phi\)

\(\hat{\mathbb P}(f_\psi(o)\ \mathrm{is\ sim})\)

\(\epsilon^k\)

\(a^k\)

o

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \max_\phi \mathbb E_{p^S_O}[\log d_\phi (f_\psi(o))] + \mathbb E_{p^R_O} [1-\log d_\phi (f_\psi(o))]

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \max_\phi \mathbb E_{p^S_O}[\log d_\phi (f_\psi(o))] + \mathbb E_{p^R_O} [1-\log d_\phi (f_\psi(o))]

Denoiser Loss

Negative BCE Loss

\(\iff\)

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

(Variational characterization of f-divergences)

Adversarial Objective

\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{JS}(p^S_{emb}, p^R_{emb})

Hypothesis:

  1. Less sensitive to \(\alpha\)
  2. Less sensitive to visual distribution shifts
  3. Improved performance for \(|\mathcal D_R|\) = 10

Initial Results

\(|\mathcal D_R| = 50\), \(|\mathcal D_S| = 500\), \(\lambda = 1\), \(\alpha = 0.5\)

Performance: 9/10 trials

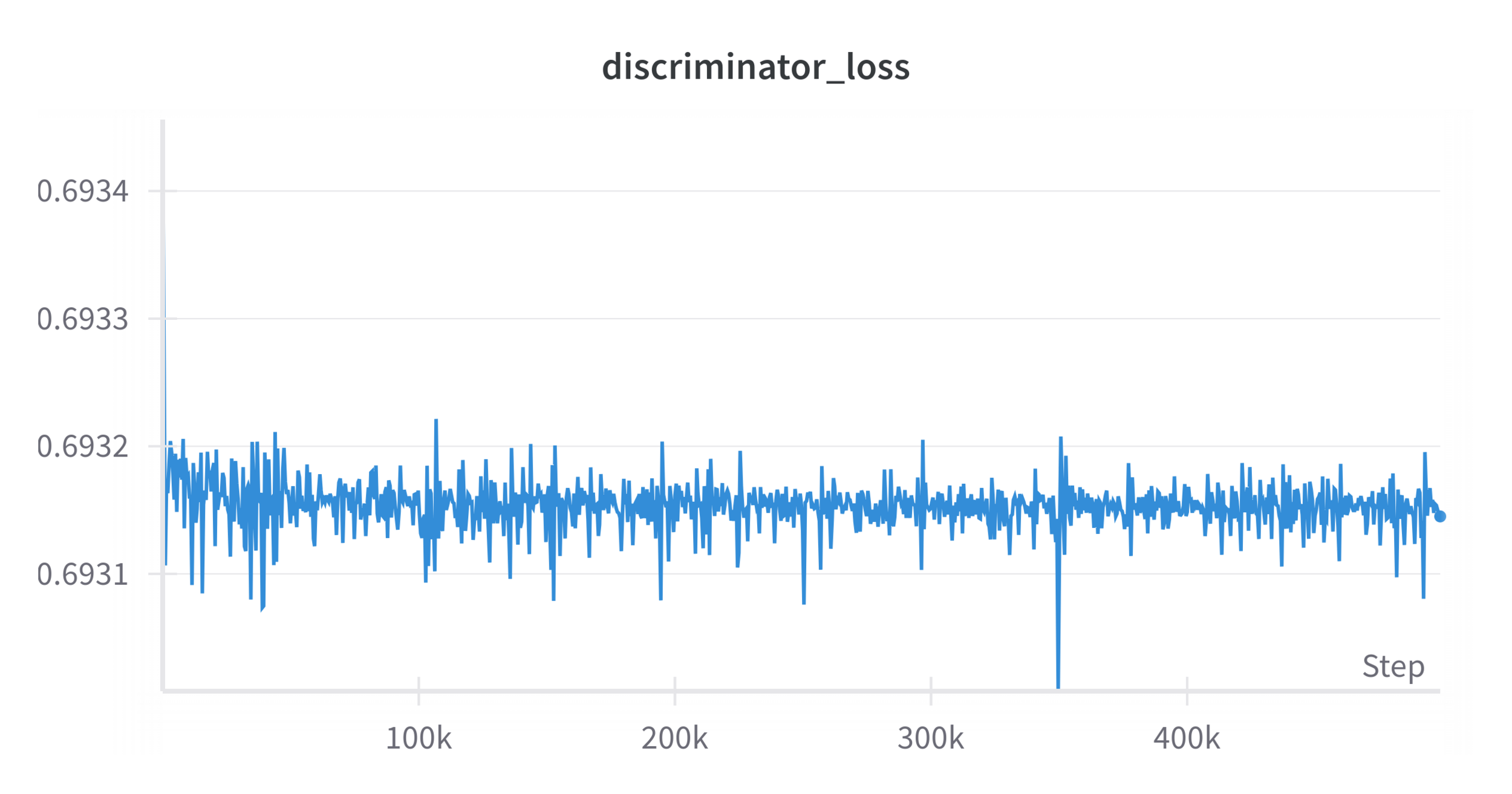
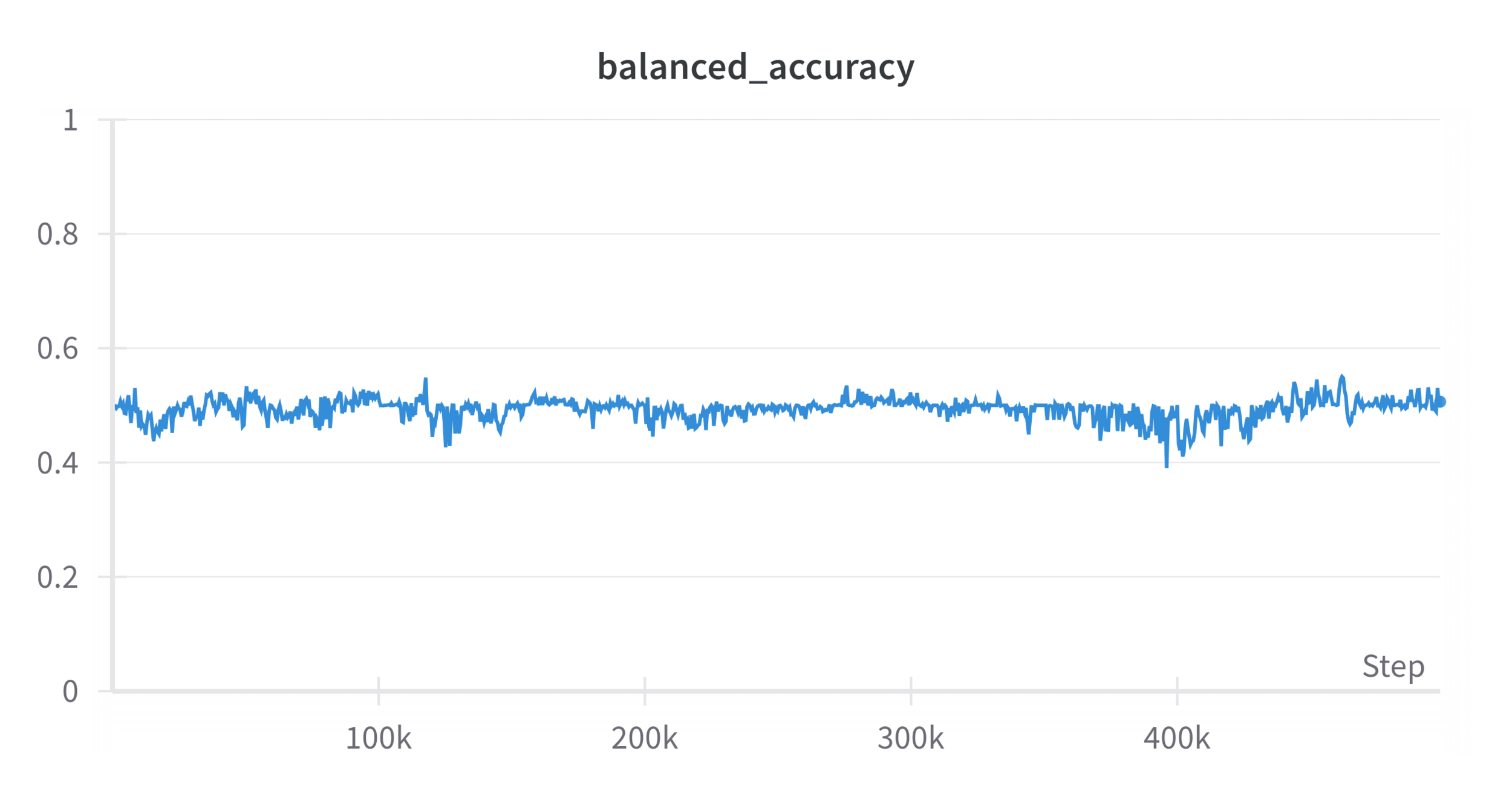
~log(2)

~50%

Problems...

  • A well-trained discriminator can still distinguish sim & real
    • This is an issue with the GAN training process (during training, the discriminator cannot be fully trained)
    • Image GAN models suffer similar problems

Potential solution?

  • Place the discriminator at the final activation?
  • Wasserstein GANs (WGANs)
\min_{\theta, \psi} \mathcal L_{\mathcal D^\alpha}(\theta, \psi) + \lambda \cdot \mathrm{W}(p^S_{emb}, p^R_{emb})

Two Philosophies For Cotraining

1. Minimize sim2real gap

  • Pros: better bounds, more performance from each data point
  • Cons: Hard to match sim and real, adversarial formulation assumes protected variables are not relevant for control

2. Embrace the sim2real gap

  • Pros: policy can identify and adapt strongly to its target domain at runtime, do not need to match sim and real
  • Cons: Doesn't enable "superhuman" performance, potentially less data efficient

Hypothesis 3

Sim data provides more information about \(p_A(a)\)

  • Sim data provides a strong prior on "likely actions" =>improves the performance of cotrained policies

We can explicitly leverage this prior using classifier free guidance

\tilde\epsilon_\theta(O, A^k,k) = (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)

Conditional Score Estimate

Unconditional Score Estimate

Helps guide the diffusion process

\mathrm{better\ est. of\ } p_A \implies \mathrm{better\ } \epsilon_\theta(\emptyset, A^k,k)

Classifier-Free Guidance

\begin{aligned} \tilde\epsilon_\theta(O, A^k,k) &= (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)\\ &=\epsilon_\theta(O, A^k,k) + \omega(\epsilon_\theta(O, A^k,k) - \epsilon_\theta(\emptyset, A^k,k)) \end{aligned}

Conditional Score Estimate

  • Term 2 guides conditional sampling by separating the conditional and unconditional action distributions
  • In image domain, this results in higher quality conditional generation

Difference in conditional and unconditional scores

Classifier-Free Guidance

\begin{aligned} \tilde\epsilon_\theta(O, A^k,k) &= (1+\omega)\epsilon_\theta(O, A^k,k) - \omega\epsilon_\theta(\emptyset, A^k,k)\\ &=\epsilon_\theta(O, A^k,k) + \omega(\epsilon_\theta(O, A^k,k) - \epsilon_\theta(\emptyset, A^k,k)) \end{aligned}
  • Due to the difference term, classifier-free guidance embraces the differences between \(p^R_{(A|O)}\) and \(p_A\)
  • Note that \(p_A\) can be provided scalably by sim and also does not require rendering observations! 

Future Work

  1. Evaluating scaling laws (sim-sim experiments)
  2. Adversarial and classifier-free guidance formulations

Immediate next steps:

Guiding Questions:

  1. What are the underlying principles and mechanisms of cotraining? How can we test them?
  2. Can we leverage these principles for algorithm design?
  3. Should cotraining minimize or embrace the sim2real gap?
  4. How can we cotrain from non-robot data (ex. video, text, etc)?

Amazon CoRo Feb 2025

By weiadam

Source: Adam Wei

Amazon CoRo Feb 2025

  • 144

More from weiadam