Learning From Bad Data In Robotics

Sept 24, 2025

Adam Wei

Agenda

Interpretations
Motion planning experiments
Sim-and-real cotraining
Scaling up "low-quality" data
Ambient Omni (locality)
Concluding thoughts

Part 1

Interpretations of Ambient Diffusion

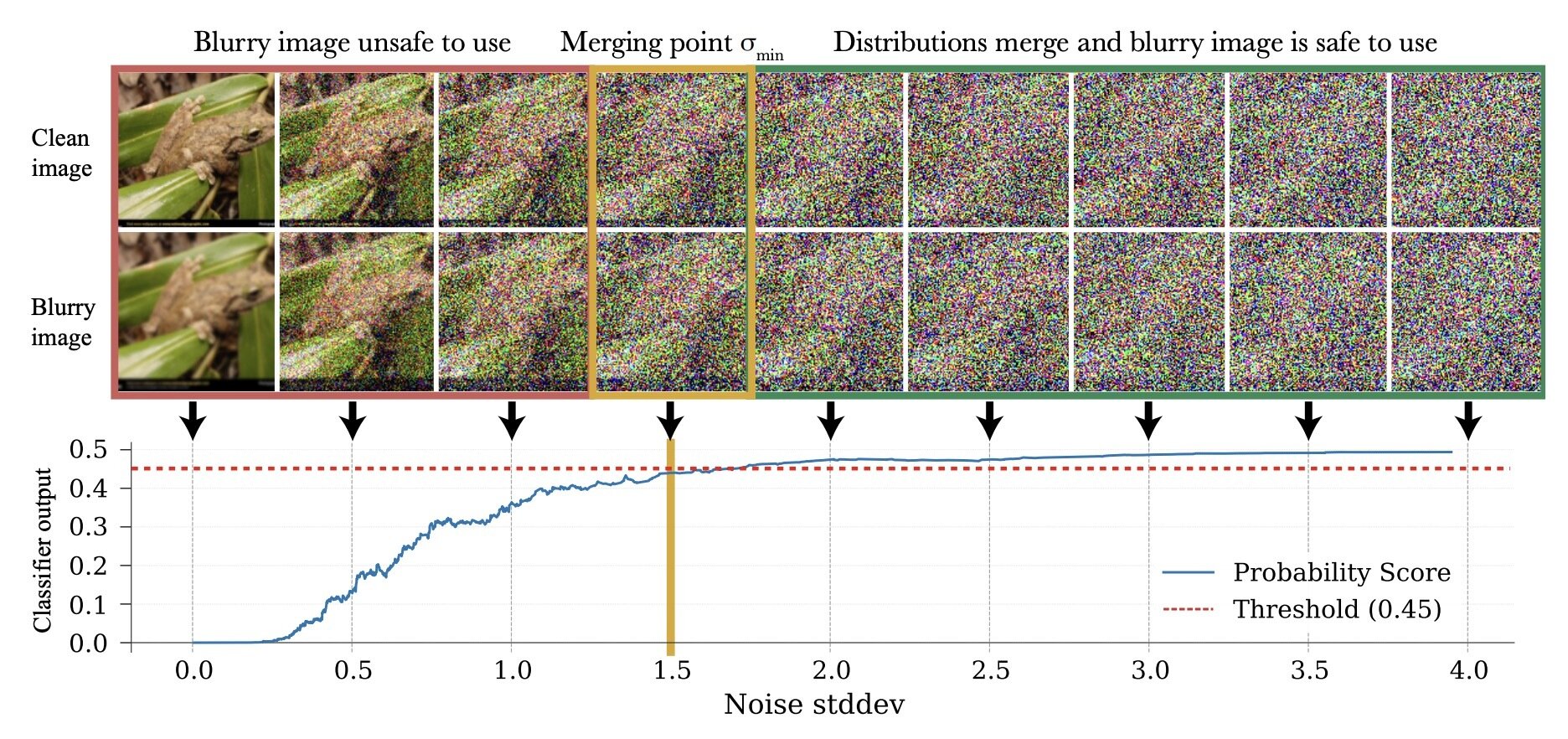
What can go wrong in [CV] data?

CC12M: 12M+ image + text captions

"Corrupt" Data:

Low quality images

"Clean" Data:

High quality images

Not just in CV: also in language, audio, robotics!

Distribution Shifts in Robot Data

Sim2real gaps
Noisy/low-quality teleop
Task-level mismatch
Changes in low-level controller

Embodiment gap
Camera models, poses, etc
Different environment, objects, etc

robot teleop

simulation

Open-X

Training on OOD Data

robot teleop

simulation

Open-X

There is still value and utility in this data!

... we just aren't using it correctlty

Goal: to develop principled algorithms that change the way we use low-quality or OOD data

"The Present"

2025

"Ambient diffusion is best in domains where good data is hard to get, but bad data is easy"

i.e. robotics?

"low data"

robot teleop

simulation

Open-X

"The Future"

2025

My bets:

"low data"

1. Robot data will be plentiful

Ex. Danny Driess (PI)

2. High quality data is hard to get

\(\implies\) this problem will remain relevant

202[?]

"big data"

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Ambient Diffusion

Repeat:

Sample \(\sigma\) ~ Unif([0,1])
Sample (O, A, \(\sigma_{min}\)) ~ \(\mathcal{D}\) s.t. \(\sigma > \sigma_{min}\)
Optimize denoising loss or ambient loss

\(\sigma=0\)

\(\sigma>\sigma_{min}\)

\(\sigma_{min}\)

*\(\sigma_{min} = 0\) for all clean samples

\(\sigma=1\)

Loss Function (for \(x_0\sim q_0\))

\(\mathbb E[\lVert h_\theta(x_t, t) + \frac{\sigma_{min}^2\sqrt{1-\sigma_{t}^2}}{\sigma_t^2-\sigma_{min}^2}x_{t} - \frac{\sigma_{t}^2\sqrt{1-\sigma_{min}^2}}{\sigma_t^2-\sigma_{min}^2} x_{t_{min}} \rVert_2^2]\)

Ambient Loss

Denoising Loss

\(x_0\)-prediction

\(\epsilon\)-prediction

(assumes access to \(x_0\))

(assumes access to \(x_{t_{min}}\))

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)

\(\mathbb E[\lVert h_\theta(x_t, t) - \epsilon \rVert_2^2]\)

\(\mathbb E[\lVert h_\theta(x_t, t) - \frac{\sigma_t^2 (1-\sigma_{min}^2)}{(\sigma_t^2 - \sigma_{min}^2)\sqrt{1-\sigma_t^2}}x_t + \frac{\sigma_t \sqrt{1-\sigma_t^2}\sqrt{1-\sigma_{min}^2}}{\sigma_t^2 - \sigma_{min}^2}x_{t_{min}}\rVert_2^2]\)

Terminology

"Good" Data

"Bad" Data

Clean
In-distribution
High-quality

Corrupt
Out-of-distribution
Low-quality

Interpations: The Role of Gaussian Noise

1. Gaussian noise = corruption

Giannis' presentation
Mirrors the development of the algorithm
"but my corruption isn't Gaussian!
- Feel unnatural...

2. Gaussian noise = contraction

More general
Better framework for reasoning about what's going on under the hood
Less jarring

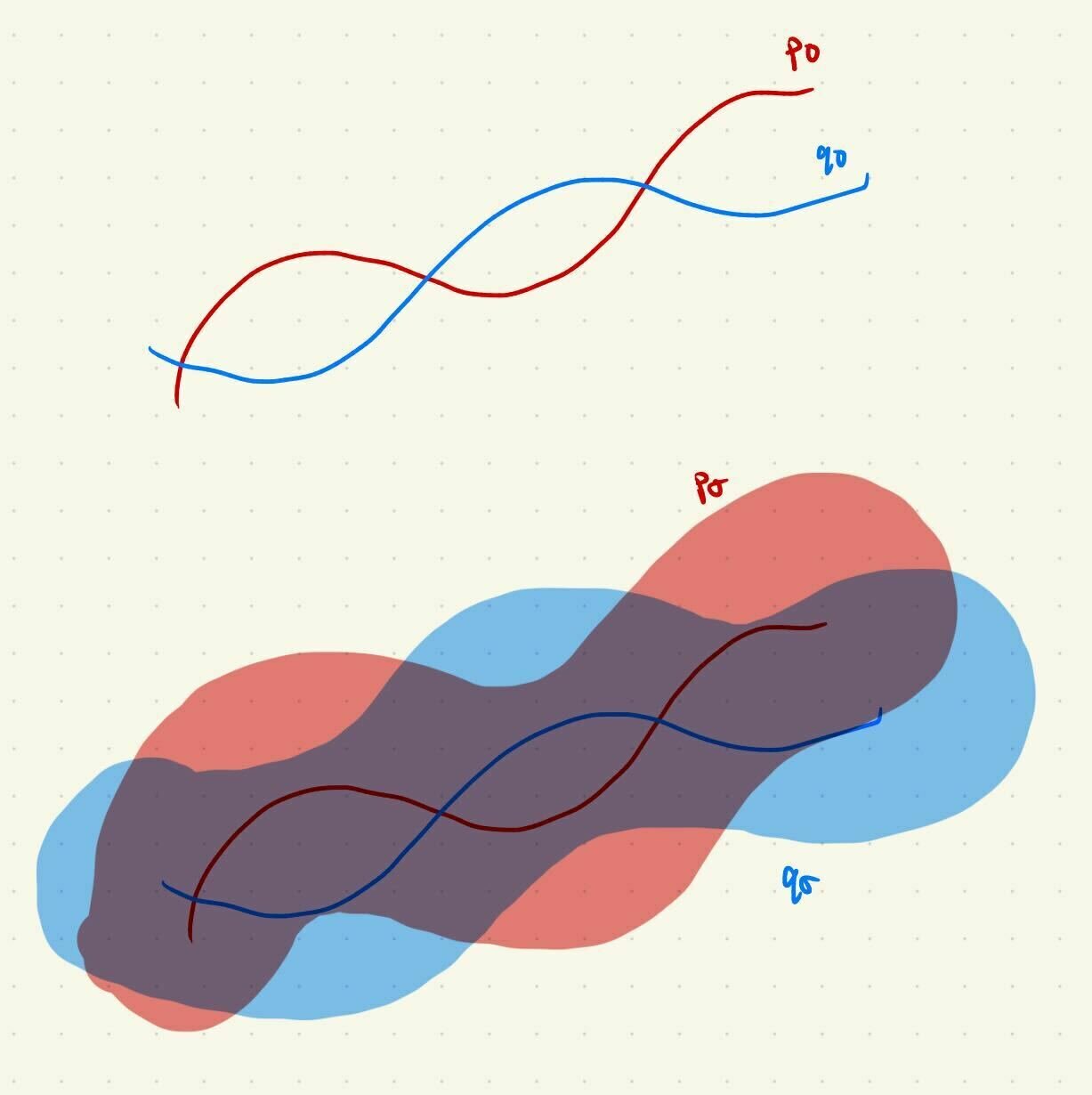
Gaussian Noise As Contraction

\(p_0\)

\(q_0\)

\(p_\sigma\)

\(q_\sigma\)

D(p_0, q_0) \geq D(p_\sigma, q_\sigma)

\(D(p_\sigma, q_\sigma) \to 0\) as \(\sigma\to \infty\)

\(\implies \exists \sigma_{min} \ \mathrm{s.t.}\ D(p_\sigma, q_\sigma) < \epsilon\ \forall \sigma > \sigma_{min}\)

Noisy Channel

\(Y = X + \sigma Z\)

Gaussian Noise As Contraction

\(p_0\)

\(q_0\)

\(p_\sigma=p_0 * \mathcal N(0, \sigma^2\mathrm{I})\)

\(q_\sigma=q_0 * \mathcal N(0, \sigma^2\mathrm{I})\)

1. "Noise as corruption": for \(\sigma > \sigma_{min}\), corruption appears Gaussian

Goal: Learn \(\nabla \log p_\sigma(x)\)

Gaussian Noise As Contraction

\(p_0\)

\(q_0\)

\(p_\sigma=p_0 * \mathcal N(0, \sigma^2\mathrm{I})\)

\(q_\sigma=q_0 * \mathcal N(0, \sigma^2\mathrm{I})\)

Goal: Learn \(\nabla \log p_\sigma(x)\)

2. "Noise as contraction": for \(\sigma > \sigma_{min}\), \(\red{\nabla \log p_\sigma (x)} \approx \blue{\nabla \log q_\sigma (x)}\)

Gaussian Noise As Contraction

Any process that contracts distributions to the same final distribution is viable!

Ex: Alex's suggestion to noise with a "notch filter"

Different ways to mix the data... more on this later ;)

Noise as contraction: for \(\sigma > \sigma_{min}\), \(\red{\nabla \log p_\sigma (x)} \approx \blue{\nabla \log q_\sigma (x)}\)

Goal: Learn \(\nabla \log p_\sigma(x)\)

Part 2

Motion Planning Experiments

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Ambient Diffusion

Repeat:

Sample \(\sigma\) ~ Unif([0,1])
Sample (O, A, \(\sigma_{min}\)) ~ \(\mathcal{D}\) s.t. \(\sigma > \sigma_{min}\)
Optimize denoising loss or ambient loss

\(\sigma=0\)

\(\sigma>\sigma_{min}\)

\(\sigma_{min}\)

*\(\sigma_{min} = 0\) for all clean samples

\(\sigma=1\)

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Choosing \(\sigma_{min}\)

Finding \(\sigma_{min}\)

Sweep? Use classifier?

Increasing granularity

Assign \(\sigma_{min}\) per datapoint

Assign \(\sigma_{min}\) per dataset

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Choosing \(\sigma_{min}\)

How to choose \(\sigma_{min}\)?

\(\sigma_{min}^i = \inf\{\sigma\in[0,1]: c_\theta (x_\sigma, \sigma) > 0.5-\epsilon\}\)

\(\implies \sigma_{min}^i = \inf\{\sigma\in[0,1]: d_\mathrm{TV}(p_\sigma, q_\sigma) = 2\epsilon\}\)*

* assuming \(c_\theta\) the best possible classifier

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Choosing \(\sigma_{min}\)

Motion Planning Experiments

Distribution shift: Low-quality, noisy trajectories

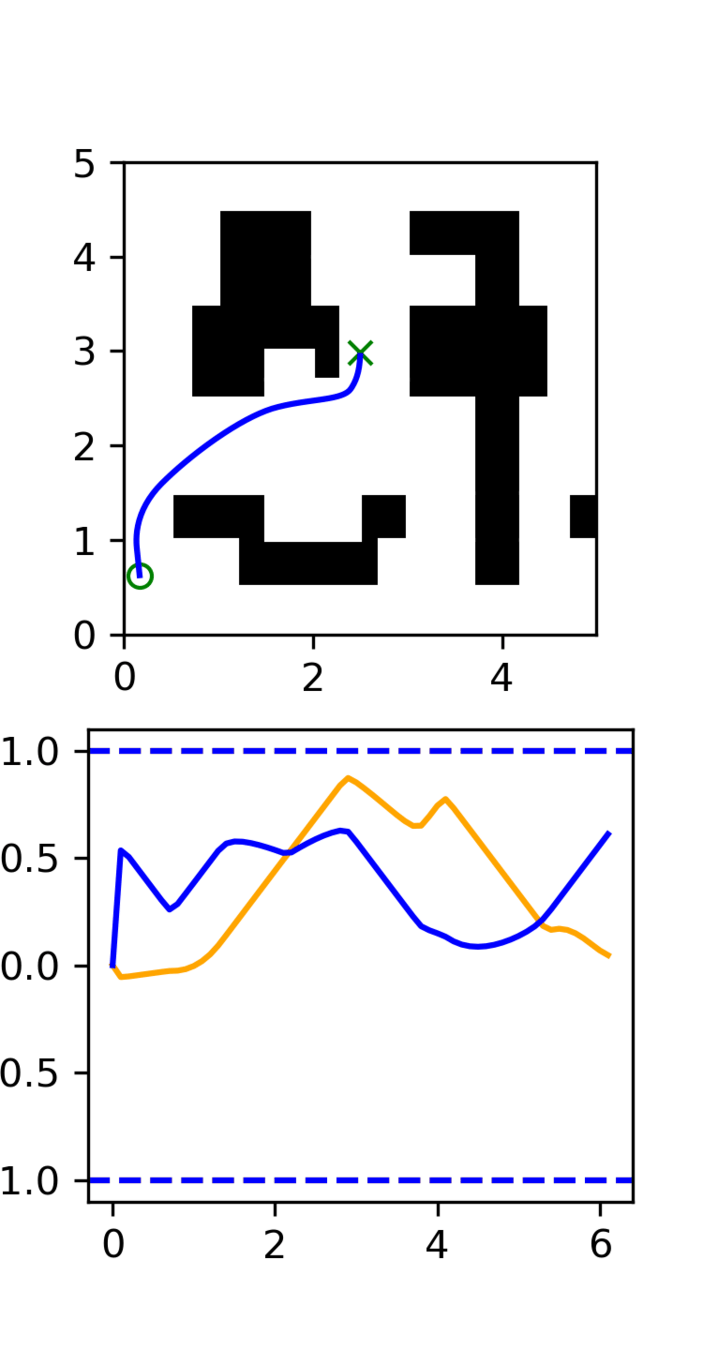
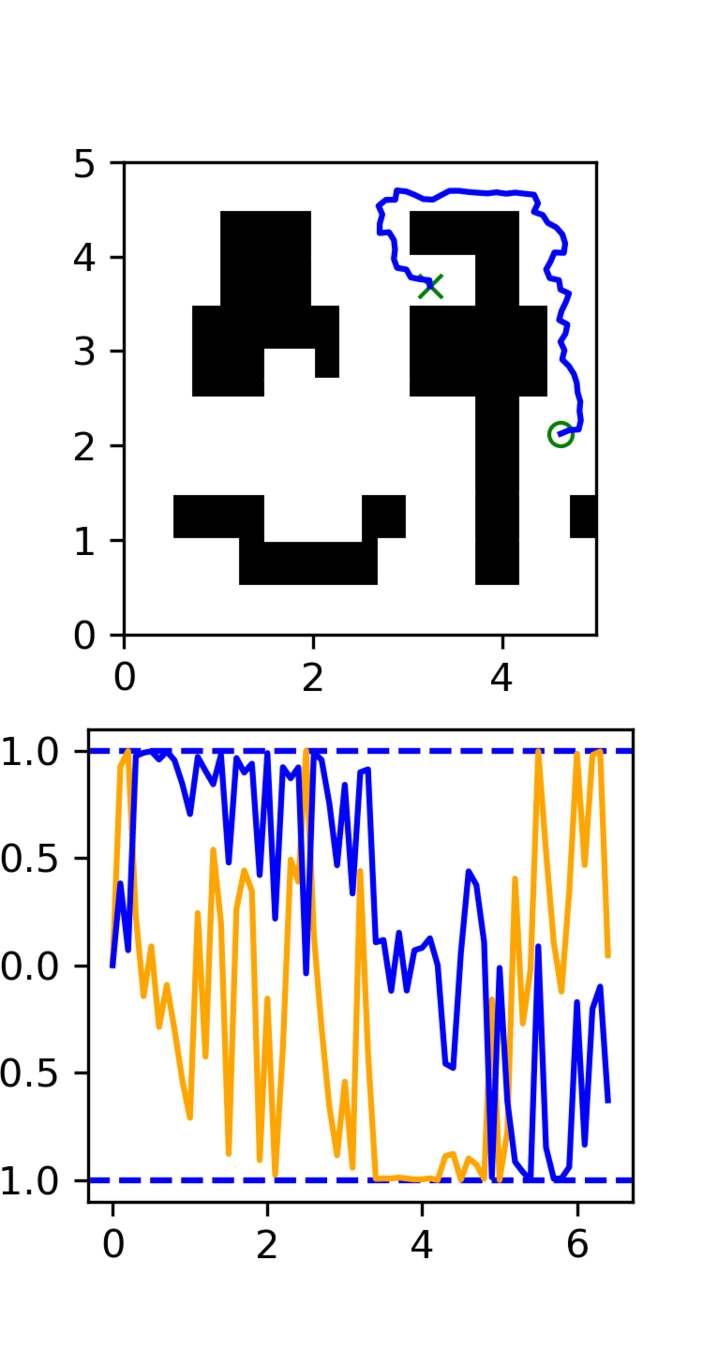
High Quality:

100 GCS trajectories

Low Quality:

5000 RRT trajectories

Note: This experiment is easily generalizable to 7-DoF robot motion planning

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Choosing \(\sigma_{min}\)

Task vs Motion Level

Distribution shift: Low-quality, noisy trajectories

\(\sigma=0\)

5000 RRT Trajectories

\(\sigma_{min}\)

\(\sigma=1\)

100 GCS Trajectories

Task level:

learn the maze structure

Motion level:

learn smooth motions

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Choosing \(\sigma_{min}\)

Results

GCS

Success Rate

(Task-level)

Avg. Jerk^2

(Motion-level)

RRT

GCS+RRT

(Co-train)

GCS+RRT

(Ambient)

50%

Swept for best \(\sigma_{min}\) per dataset

Policies evaluated over 100 trials each

100%

7.5k

17k

91%

14.5k

98%

5.5k

Loss Function

Loss Function (for \(x_0\sim q_0\))

Denoising Loss vs Ambient Loss

Choosing \(\sigma_{min}\)

Qualitative Results

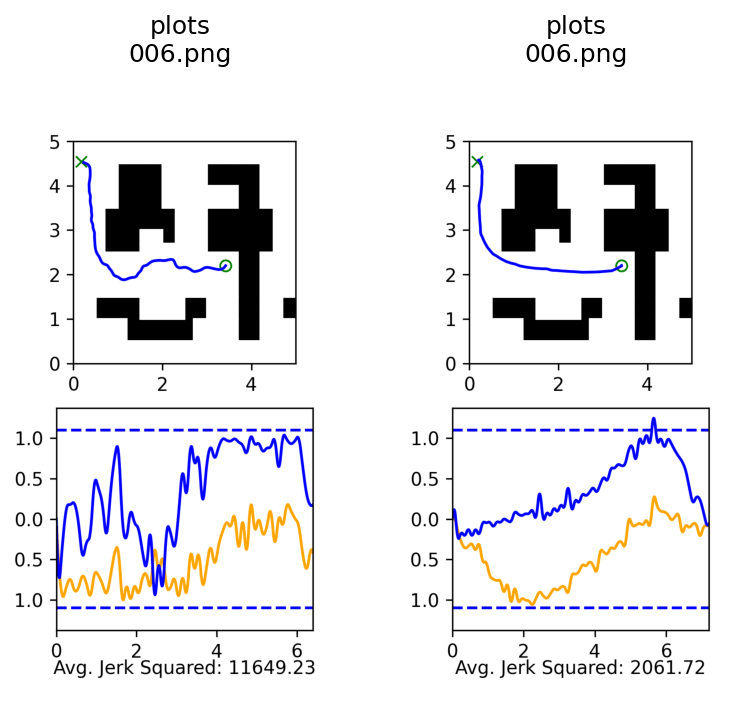
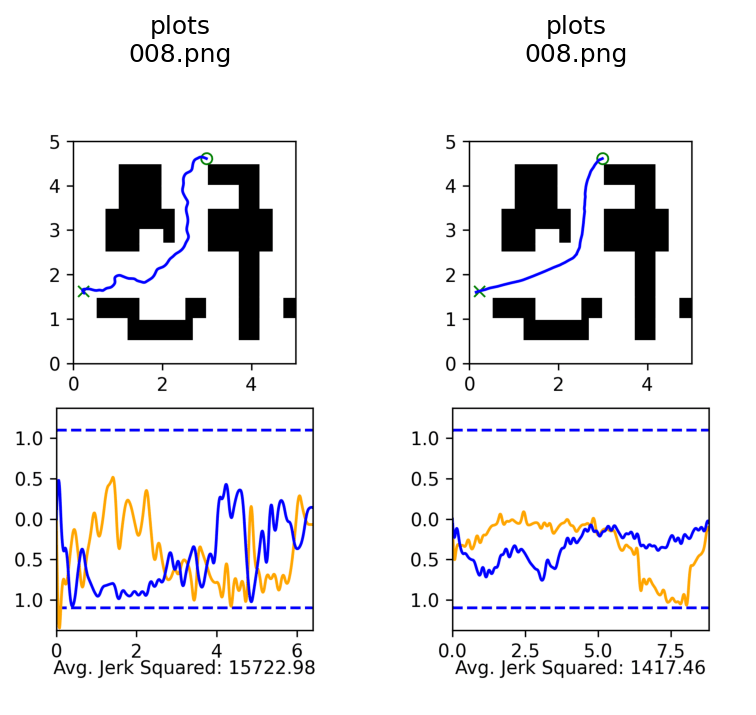
Co-trained

Ambient

Part 3

Sim-and-Real Cotraining

Sim & Real Cotraining

Distribution shift: sim2real gap

In-Distribution:

50 demos in "target" environment

Out-of-Distribution:

2000 demos in sim environment

Experiments

Experiment 1: swept \(\sigma_{min}\) per dataset

Experiment 2: estimated \(\sigma_{min}\) per datapoint with a classifier

Caveat! Classifier was trained to predict sim vs real actions

ie. trained to distinguish \(p(A)\) and \(q(A)\)
as opposed to \(p(A|O)\) and \(q(A | O)\)

Experiment 3: exploring ambient diffusion at different data scales

Experiments 1 & 2

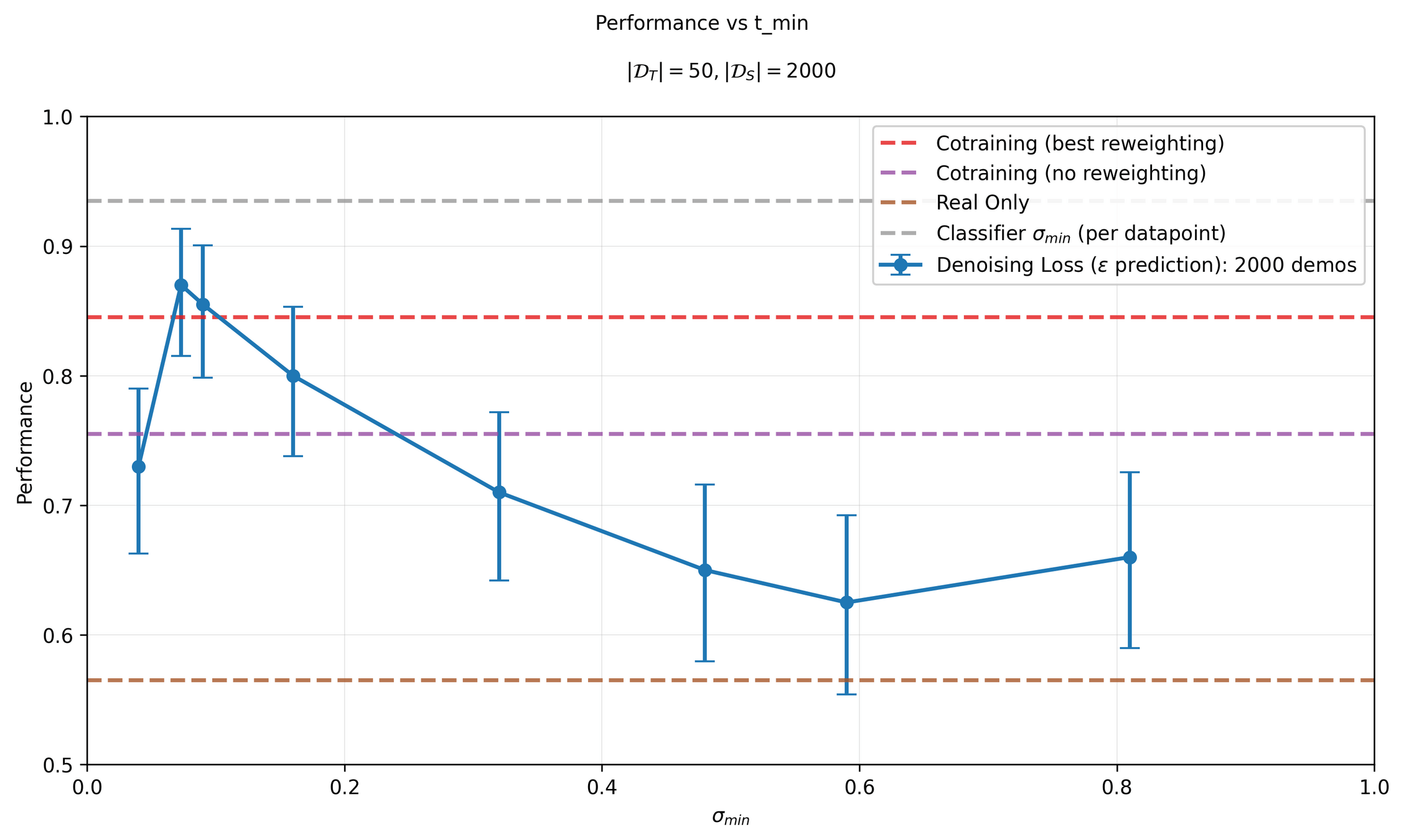
Moving forwards, all experiments will use the classifier

10 Real Demos

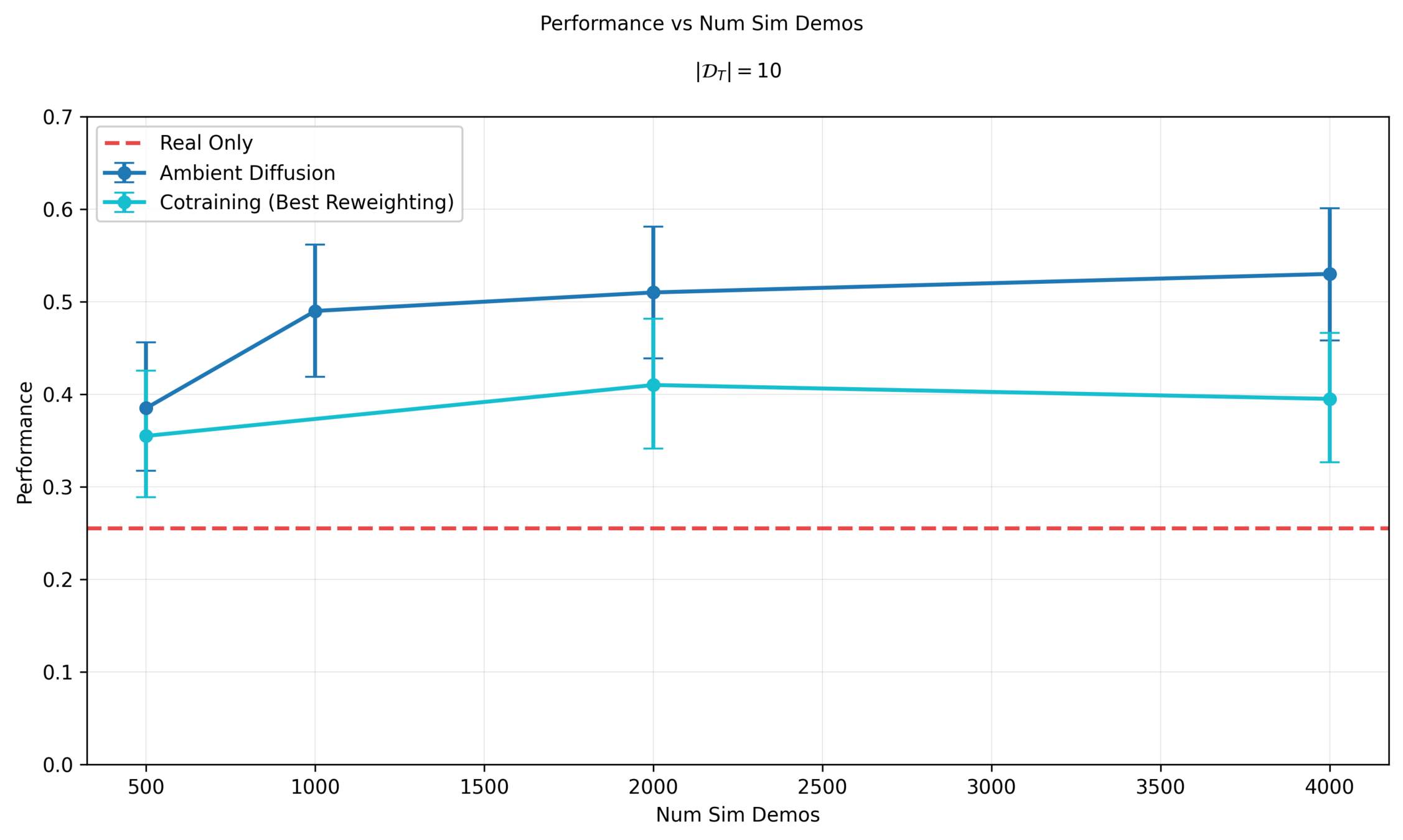
50 Real Demos

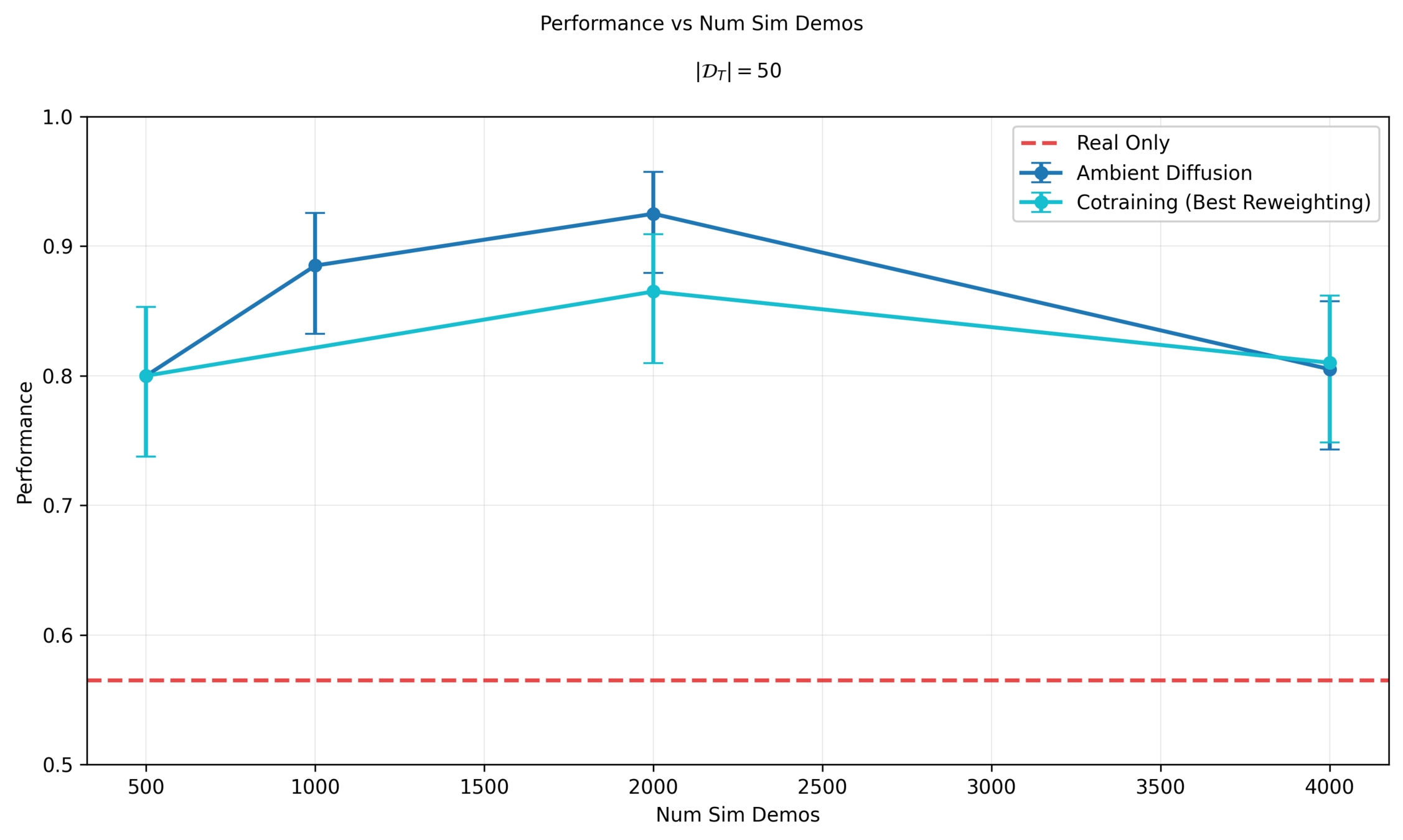
Part 4

Scaling Low-Quality Data

Denoising Loss vs Ambient Loss

Whats going wrong?

Problem 1

Classifier biases data distribution at different noise-levels

Denoising Loss vs Ambient Loss

What's going wrong?

Let's examine the problems one at a time...

Ambient \(\to\) sim-only as \(|\mathcal{D}_S| \to \infty\)

... and sim-only is bad!

Classifier biases data distribution at different noise-levels

Problem 1

Problem 2

Denoising Loss vs Ambient Loss

Problem 1: Biasing from classifier

Some "types" of data are more likely to be assigned low \(\sigma_{min}\)

This biases the training distribution, and thus the sampling distribution

Denoising Loss vs Ambient Loss

Thought Experiment

\(q_0\) =

w.p. \(\frac{1}{2}\)

\(p_0\) =

w.p. \(\frac{1}{2}\)

Denoising Loss vs Ambient Loss

Thought Experiment

\(q_0\) =

w.p. \(\frac{1}{2}\)

Training becomes biased towards dogs
In the limit of \(\infty\) samples from \(q_0\), we will only generate dogs!!

not in \(p_0\)

\(\implies\) \(\sigma_{min}\approx 1\)

(dont use this data)

in \(p_0\)

\(\implies\) \(\sigma_{min}\approx 0\)

(use this data!)

Denoising Loss vs Ambient Loss

Is Problem 1 real?

Mode 1

Mode 2

Mode 3

Mode 4

Denoising Loss vs Ambient Loss

Is Problem 1 real?

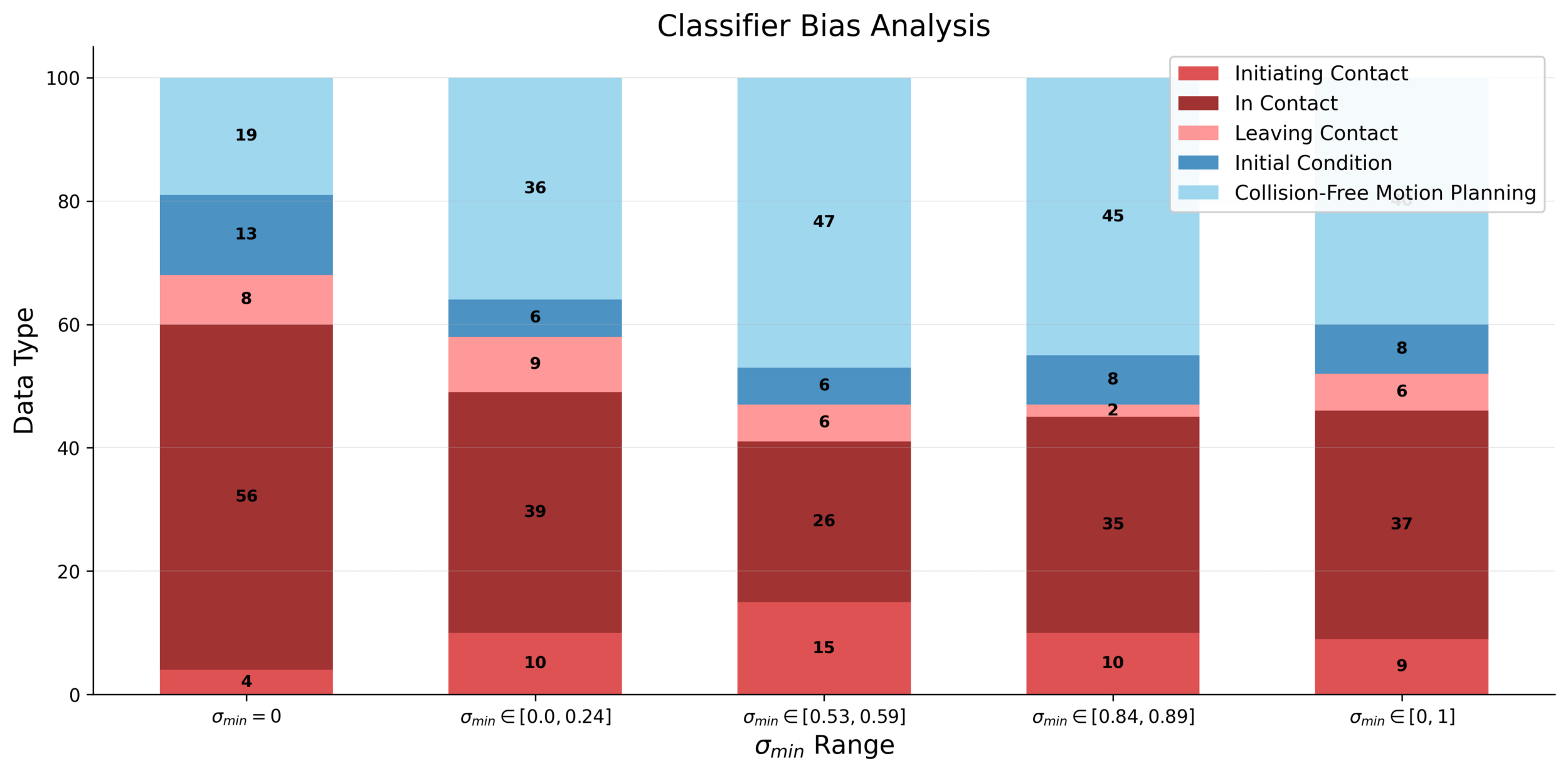
Mode 1

Mode 2

Mode 3

Mode 4

Denoising Loss vs Ambient Loss

Solution: Bucketing

"Can't do statistics with n=1" - Costis

Increasing granularity

Assign \(\sigma_{min}\) per datapoint

Assign \(\sigma_{min}\) per dataset

Assign \(\sigma_{min}\) per bucket

Split dataset into N buckets

\(N=1\)

\(N=|\mathcal{D}|\)

Denoising Loss vs Ambient Loss

Solution: Bucketing

How to bucket?

Randomly per datagram
Randomly per episode
Find \(\sigma^i_{min}\) per datapoint; assign buckets in order of increasing \(\sigma^i_{min}\)

Increasing granularity

Assign \(\sigma_{min}\) per datapoint

Assign \(\sigma_{min}\) per dataset

Assign \(\sigma_{min}\) per bucket

\(N=1\)

\(N=|\mathcal{D}|\)

Denoising Loss vs Ambient Loss

Solution: Bucketing

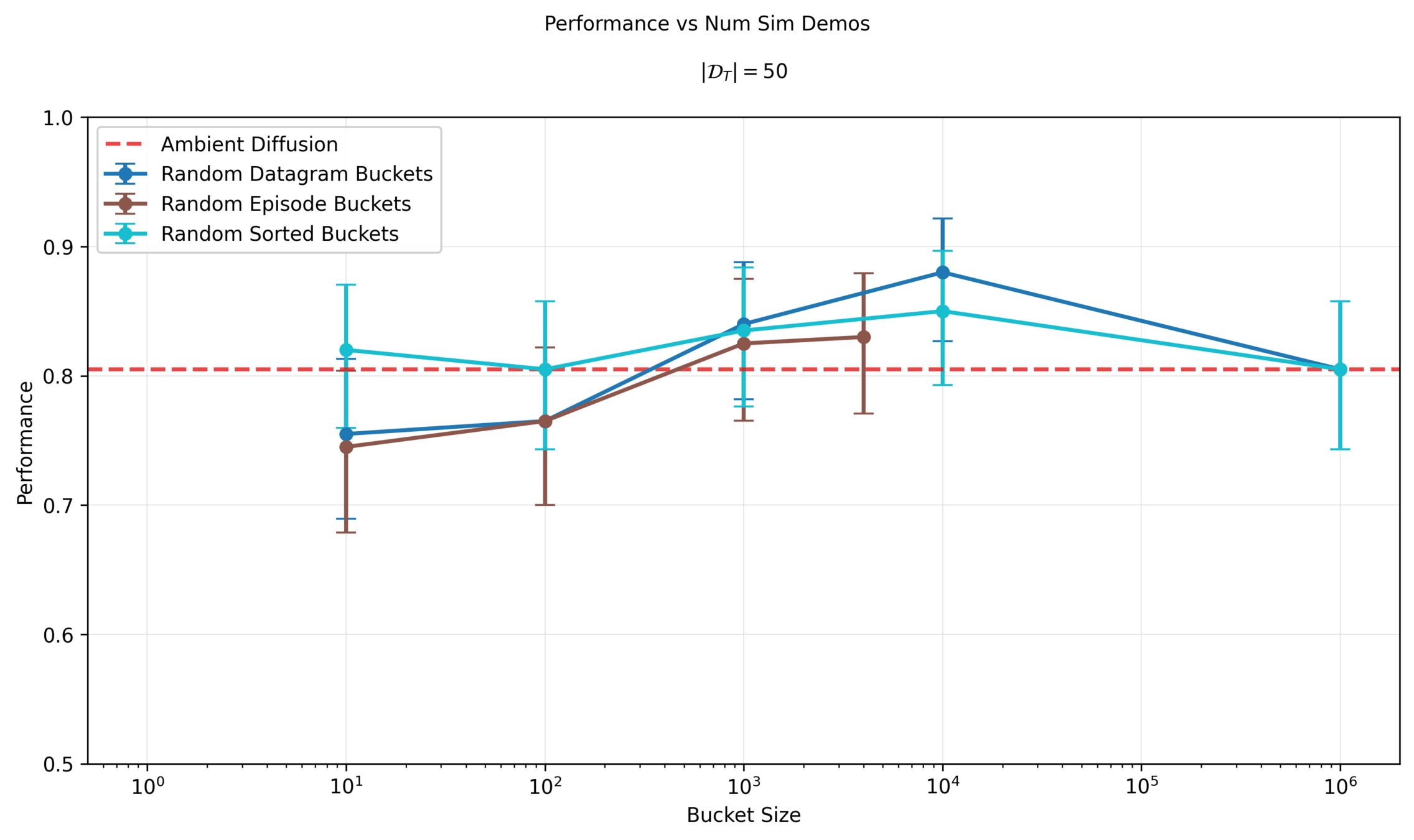
Denoising Loss vs Ambient Loss

Solution: Bucketing

What's going wrong?

Solution: bucketing

Ambient \(\to\) sim-only as \(|\mathcal{D}_S| \to \infty\)

... and sim-only is bad!

Classifier biases data distribution at different noise-levels

Problem 1

Problem 2

Denoising Loss vs Ambient Loss

Problem 2: Ambient \(\to\) sim-only

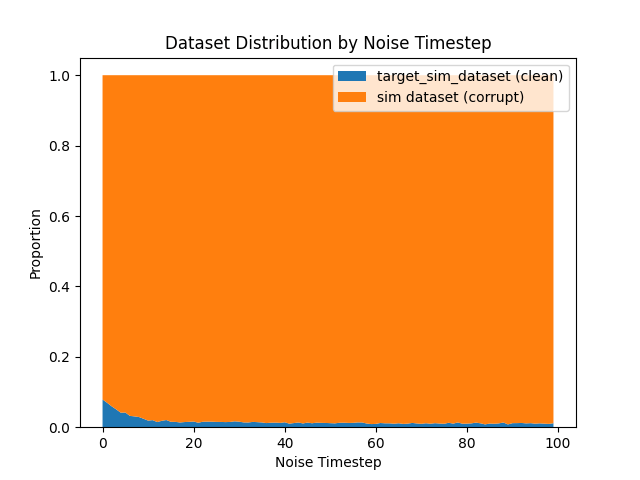
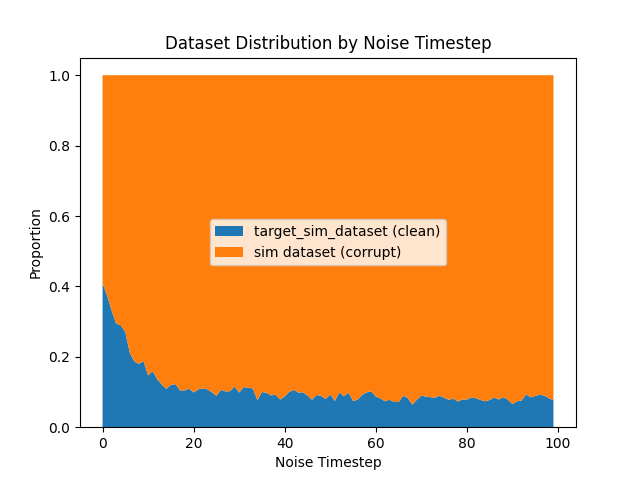
\(|\mathcal{D}_S|=500\)

\(|\mathcal{D}_S|=4000\)

Sampling procedure:

Sample \(\sigma\) ~ Unif([0,1])
Sample (O, A, \(\sigma_{min}\)) ~ \(\mathcal{D}\) s.t. \(\sigma > \sigma_{min}\)

Denoising Loss vs Ambient Loss

Solution: "Soft" Ambient Diffusion

"Doesn't make sense to use a hard threshold" - Pablo

(I am paraphrasing...)

Hard threshold!

\(\sigma=1\)

\(\sigma=0\)

\(\sigma=\sigma_{min}\)

Corrupt Data (\(\sigma_>\sigma_{min}\))

Clean Data (\(\sigma_{min}=0\))

Denoising Loss vs Ambient Loss

Different \(\alpha_\sigma\) per \(\sigma\in [0, 1]\)

"Doesn't make sense to use a hard threshold" - Pablo

(I am paraphrasing...)

\(\sigma=1\)

\(\sigma=0\)

Clean Data

Corrupt Data

Soft Ambient: ratio of clean to corrupt is a function of \(\alpha_\sigma\)

Ambient: ratio of clean to corrupt is a function of dataset size

Denoising Loss vs Ambient Loss

Why this should work

Optimal mixing ratio is a function of:

Size of dataset 1
Size of dataset 2
\(D(p, q)\)

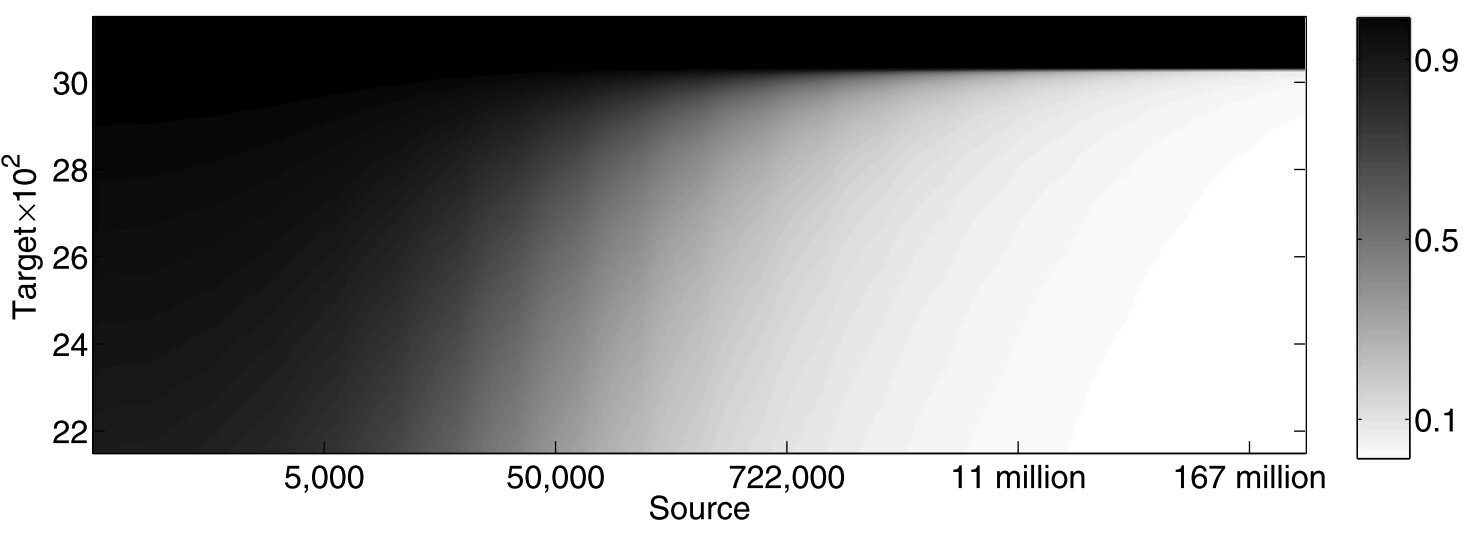
Ex. In binary classification and fixed \(D(p,q)\)...

Ben-David et. al, A theory of learning from different domains, 2009

Denoising Loss vs Ambient Loss

Why this should work

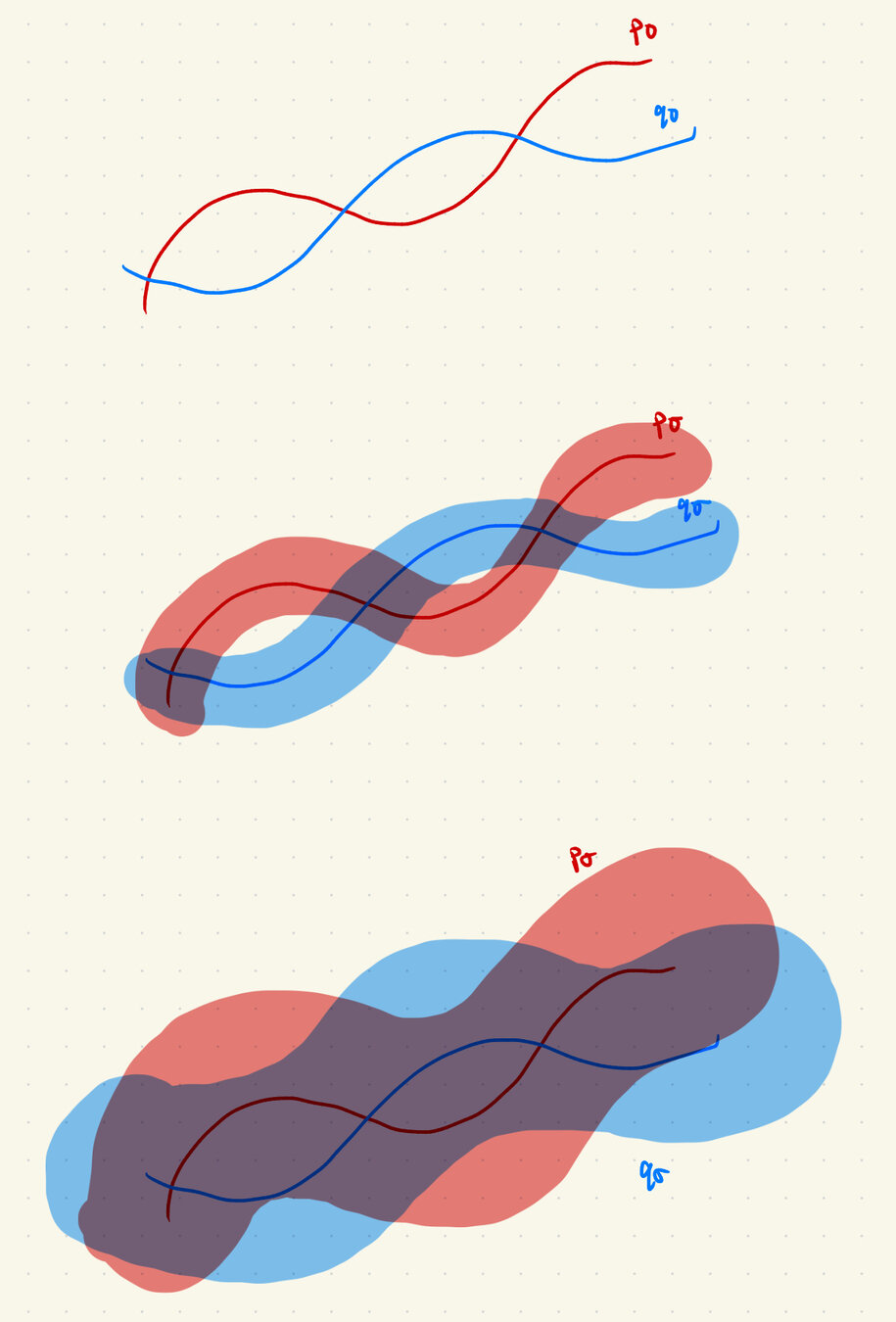
\(\sigma\)

\(D(p_\sigma, q_\sigma)\)

ratio for "bad" data

This idea is fits naturally in the noise as contraction interpretation.

Denoising Loss vs Ambient Loss

How to find \(\alpha^*(\sigma, n_1, n_2)\)

Have some ideas to find \(\alpha^*\) based on theoretical bounds...

... first try linear function just to get some signal.

\(\sigma=1\)

\(\sigma=0\)

Clean Data

Corrupt Data

Denoising Loss vs Ambient Loss

Will hopefully fix scaling issues?

Solution: bucketing

Ambient \(\to\) sim-only as \(|\mathcal{D}_S| \to \infty\)

... and sim-only is bad!

Classifier biases data distribution at different noise-levels

Problem 1

Problem 2

Solution: soft ambient

Part 5

Ambient Omni

Denoising Loss vs Ambient Loss

Locality

Ambient: "use low-quality data at high noise levels"

Ambient Omni: "use low-quality data at low and high noise levels"

Leverages locality structure in many real world datasets

Denoising Loss vs Ambient Loss

Locality

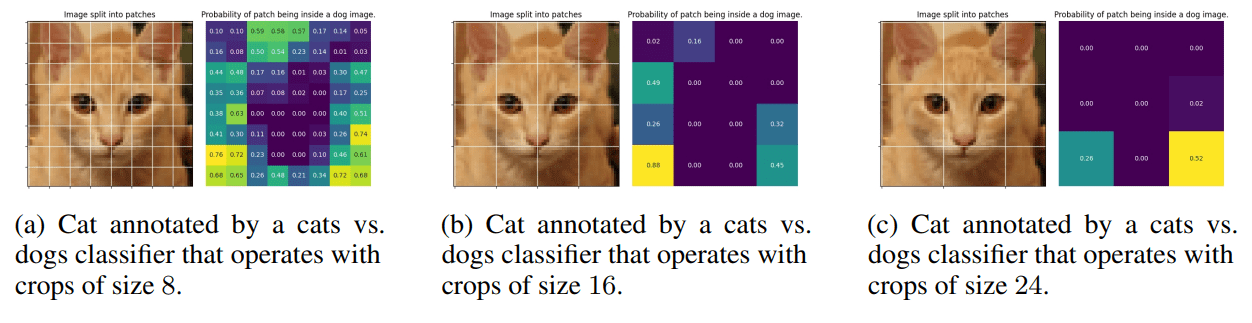
Which photo is the cat?

Denoising Loss vs Ambient Loss

Locality

Which photo is the cat?

Which photo is the cat?

Locality

Which photo is the cat?

Locality

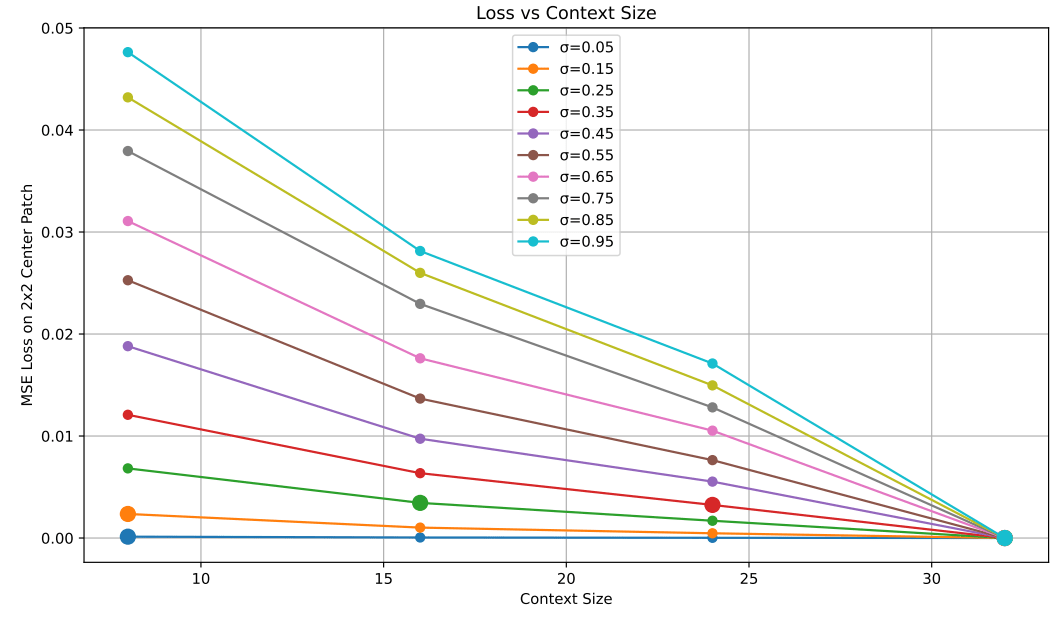
Loss vs Receptive Field

Receptive Field vs \(\sigma\)

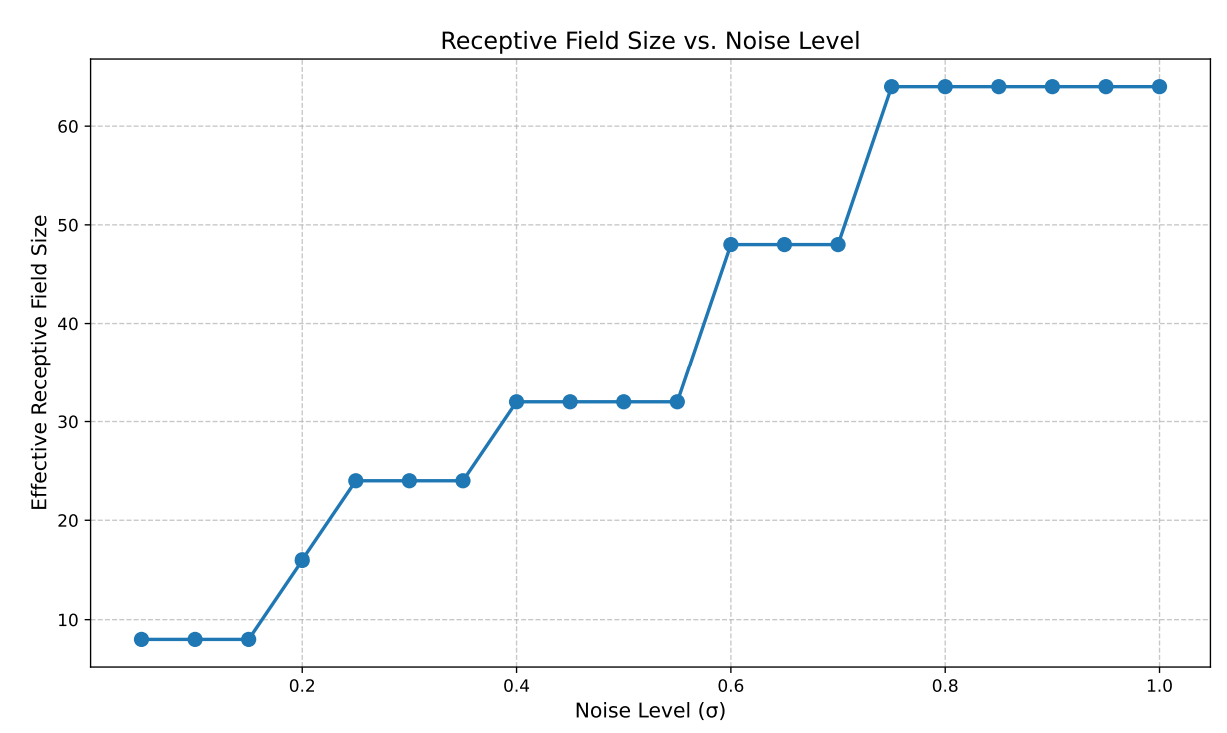
receptive field = \(f(\sigma)\)

Leveraging Locality

Intuition

If \(p_\sigma \approx q_\sigma\) at receptive field \(f(\sigma)\), then \(q_\sigma\) can be used to learn \(p_\sigma\)

The largest such \(\sigma\) is \(\sigma_{max}\)

receptive field = \(f(\sigma)\)

Ambient Omni

Repeat:

Sample \(\sigma\) ~ Unif([0,1])
Sample (O, A, \(\sigma_{min}, \sigma_{max}\)) ~ \(\mathcal{D}\) s.t. \(\sigma \in [0, \sigma_{max}) \cup (\sigma_{min}, 1]\)
Optimize denoising loss or ambient loss

\(\sigma=0\)

\(\sigma>\sigma_{min}\)

\(\sigma_{min}\)

*\(\sigma_{min} = 0\) for all clean samples

\(\sigma=1\)

\(\sigma_{max}\)

\(\sigma>\sigma_{min}\)

\(\sigma_{max}\)

Implication for Robotics

\(\sigma=0\)

\(\sigma>\sigma_{min}\)

\(\sigma_{min}\)

\(\sigma=1\)

\(\sigma_{max}\)

\(\sigma>\sigma_{min}\)

\(\sigma_{max}\)

Task level

Motion level

Data can be corrupt on the motion level and/or the task level
Ambient handles motion level corruption
Ambient Omni handles task level corruption as well

Example: Bin Sorting

Distribution shift: task level mismatch, motion level correctness

In-Distribution:

50 demos with correct sorting logic

Out-of-Distribution:

200 demos with arbitrary sorting

Example: Bin Sorting

Distribution shift: task level mismatch, motion level correctness

Contrived experiment... but it effectively illustrates the effect of \(\sigma_{max}\)

In-Distribution

Out-of-Distribution

Example: Bin Sorting

Contrived experiment... but it effectively illustrates the effect of \(\sigma_{max}\)

Repeat:

Sample \(\sigma\) ~ Unif([0,1])
Sample (O, A, \sigma_{max}\)) ~ \(\mathcal{D}\) s.t. \(\sigma \in [0, \sigma_{max})\)
Optimize denoising loss

\(\sigma=0\)

\(\sigma=1\)

\(\sigma_{max}\)

\(\sigma>\sigma_{min}\)

\(\sigma_{max}\)

Results

Diffusion

Score

(Task + motion)

Correct logic

(Task level)

Cotrain

Completion

(Motion level)

Ambient-Omni

(\(\sigma_{max}=0.24\))

70.4%

48%

High...

55.2%

88%

Low...

94.0%

88%

97.5%

Results

Diffusion

Correct logic

(Task level)

Cotrain

(task conditioned)

Completion

(Motion level)

Ambient-Omni

(\(\sigma_{max}=0.24\))

70.4%

48%

High...

55.2%

88%

Low...

88.8%

86%

92.5%

94.0%

88%

97.5%

Score

(Task + motion)

Sweeping \(\sigma_{max}\): Task-Level Metrics

Motion Planning*

Task

Planning*

* not a binary distinction!!

Sweeping \(\sigma_{max}\): Motion Planning Metrics

Motion Planning

Task

Planning

* not a binary distinction!!

Sweeping \(\sigma_{max}\): Motion Planning Metrics

Motion Planning

Task

Planning

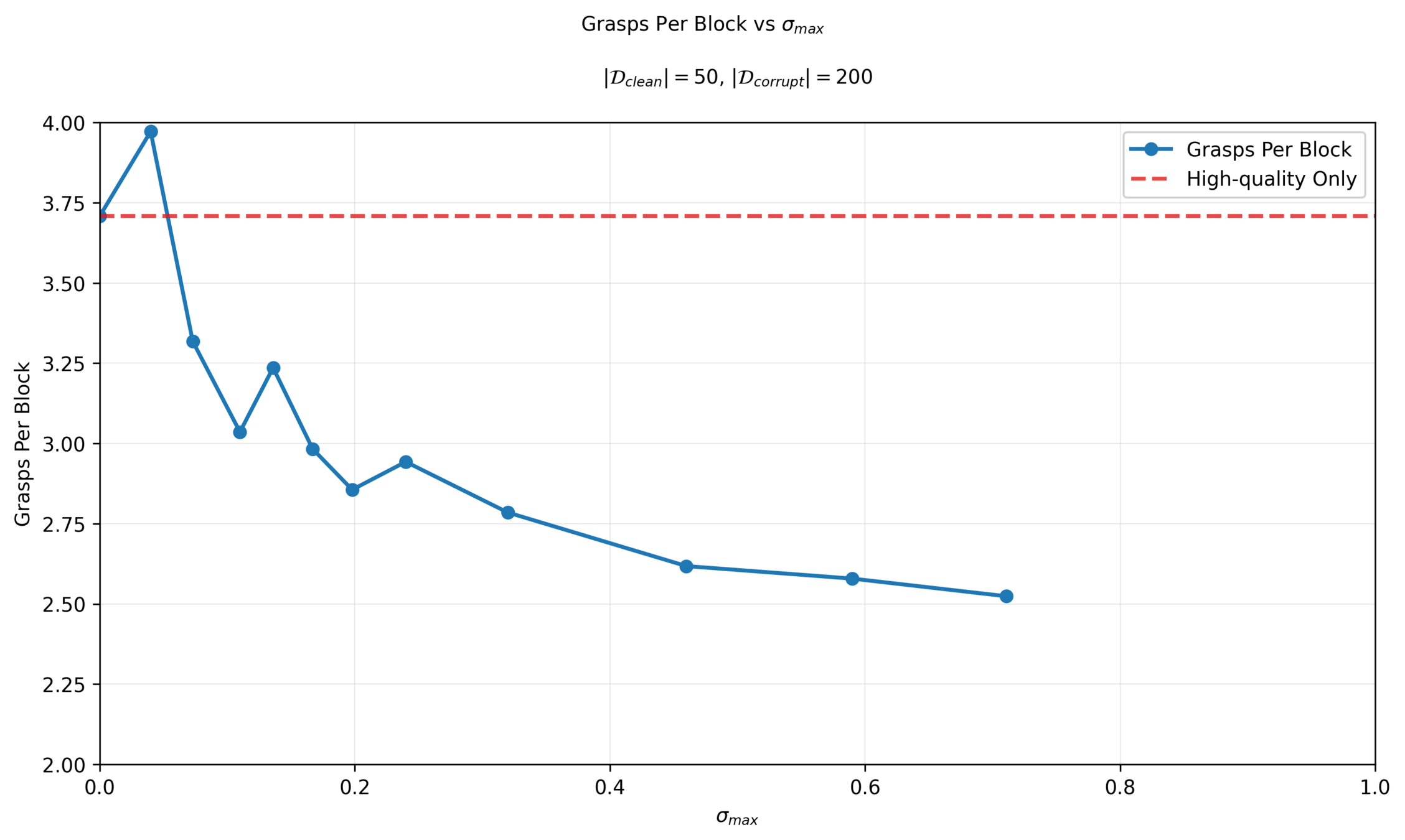
* not a binary distinction!!

Example: Bin Sorting

Distribution shift: task level mismatch, motion level correctness

In-Distribution

Out-of-Distribution

Open-X

Part 6

Concluding Thoughts

Project Roadmap

North Star Goal: Train with internet scale data (Open-X, AgiBot, etc)

So far: "Stepping stone" experiments

Each experiment tests a specific part of the algorithm

Please suggest task ideas! Think big!

Revisting Distribution Shifts

Sim2real gaps
Noisy/low-quality teleop
Task-level mismatch
Changes in low-level controller

Embodiment gap
Camera models, poses, etc
Different environment, objects, etc

robot teleop

simulation

Open-X

Sim2real gaps
Noisy/low-quality teleop
Task-level mismatch
Changes in low-level controller

Embodiment gap
Camera models, poses, etc
Different environment, objects, etc

Revisting Distribution Shifts

Sim2real gaps
Noisy/low-quality teleop
Task-level mismatch
Changes in low-level controller

Embodiment gap
Camera models, poses, etc
Different environment, objects, etc

Observation space is a key part of robot data
Currently not reasoning about corruption in the observations...

Revisting Distribution Shifts

Project Roadmap

Sim2real gaps
Noisy/low-quality teleop
Task-level mismatch
Changes in low-level controller

Embodiment gap
Camera models, poses, etc
Different environment, objects, etc

Open-X

Project Roadmap

Open-X

Variant of Ambient Omni

Cool Task!!

(TBD)

Cool Demo!!

Thank you!! (please suggest tasks...)

RLG Fall 2025 Long Talk: Learning From Low-Quality Data

By weiadam

RLG Fall 2025 Long Talk: Learning From Low-Quality Data