遞迴
遞迴(recursion)
在數學跟電腦科學上
函數定義中使用自身的方法
也就是一直呼叫自己
舉個例子
等差級數聽過吧
今天如果有個等差數列:
a_1\ =\ 1\\
a_n\ =\ a_1\ +\ (n-1)
遞迴(recursion)
a_1\ =\ 1\\
a_n\ =\ a_1\ +\ (n-1)
出來的結果應該長這樣
1,2,3,4,5.....
那如果用遞迴式表示呢?
我們可以發現第n項是他n-1項再+1
遞迴(recursion)
a_1\ =\ 1\\
a_n\ =\ a_{n-1}\ +\ 1
所以是不是可以表示成
這就是數學上遞迴式的樣子
那要怎麼寫成程式語言呢
它包含兩個組成要素
1.初始值(終止條件)
2.處理問題的方法
遞迴(recursion)
在程式語言中
遞迴的意思是函式內呼叫自己
int f(int x){
if(x==1)return 1;
return f(x-1)+1;
}
這個例子有點太過複雜化這個問題
其實可以直接cout<<x
不過畢竟是遞迴 先用簡單的例子慢慢理解
遞迴(recursion)
再用一個例子
int f(int x){
if(x==1)return 1;
return f(x-1)+x;
}
可以看出這個是用來解決什麼問題的嗎
當x=1回傳1
否則
a_x=a_{x-1}+x
遞迴(recursion)
int f(int x){
if(x==1)return 1;
return f(x-1)+x;
}
a_x=a_{x-1}+x
a_{x-1}=a_{x-2}+x-1
a_{x-2}=a_{x-3}+x-2
.
.
.
a_2=a_1+2
a_1=1
遞迴(recursion)
int f(int x){
if(x==1)return 1;
return f(x-1)+x;
}
會發現最後的結果是
1+2+......+(x-2)+(x-1)+x
也就是1加到x
x*(x+1)/2
也就是這個式子
遞迴(recursion)
接下來講遞迴的思考脈絡和組成
1.我們會發現大問題拆分成小問題
2.小問題可以拆分成更小的問題
3.每當小問題解決後 大問題也可以用小問題的結果解決
4.除了最小的問題以外 其餘都可以由相同方式解決
5.所以可以透過套用相同函式自己幫自己解決問題
以上就是遞迴的基本核心精神
遞迴(recursion)
會用在哪裡?
枚舉、分治、dfs、線段樹
以前的APCS第三題有蠻多的
之後也能為dp有些啟發性的想法
遞迴(recursion)
接著來講例題
- 費事數列
- 快速冪
- 河內塔
費事數列
費事數列
很經典的遞迴例子
費波那契數列:每一項是由前兩項相加而得
該如何用遞迴解決呢
首先我們會發現第n項的值
是由n-1和n-2項加起來
第1項的值是0
第2項的值是1
這是數列的前兩項
費事數列
a_1=0\\
a_2=1\\
a_n=a_{n-1}+a_{n-2}
遞迴式出來了
接著把它轉成程式語言
費事數列
int f(int n){
if(n==1)return 0;
if(n==2)return 1;
return f(n-1)+f(n-2);
}第1,2項是0,1
其他情況都是由前兩項加起來
遞迴下去會長怎樣呢
費事數列
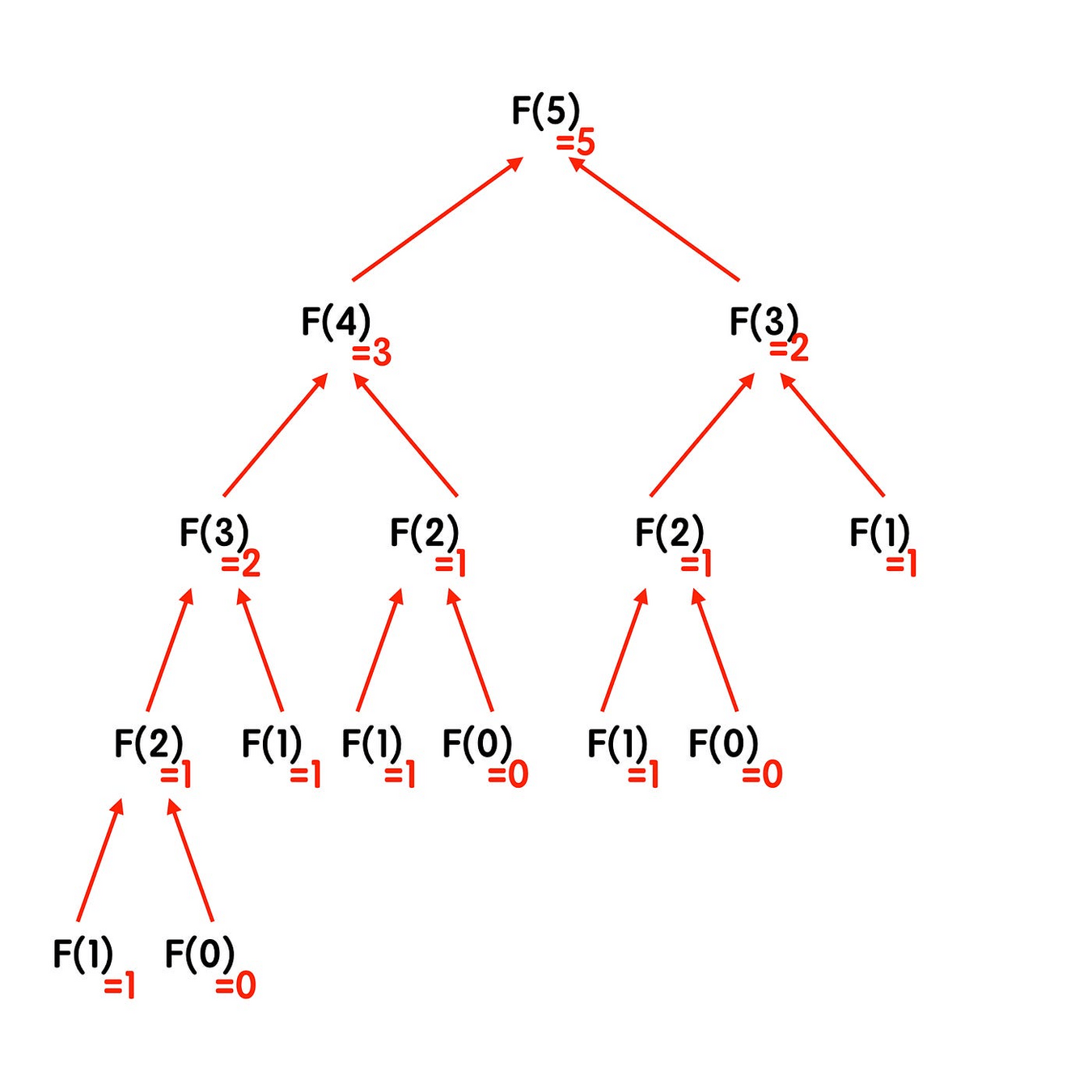
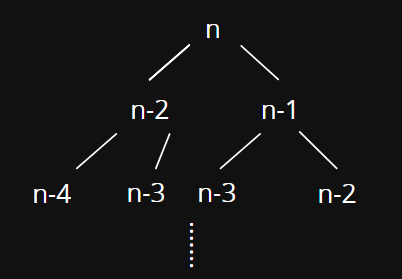
費事數列
今天測資大一點 比如45
他跑的時間花太久了 會TLE
那要怎麼改善呢
費事數列
我們可以發現甚麼?
一直做下去的話只會有更多重複的
那如果今天已經知道f(n-2)的值還需要分割成小問題繼續遞迴嗎?
費事數列
今天如果我們把重複的東西用一個陣列記下來
每次要用到的時候就可以直接取值
int tmp[1000005];
int f(int n){
if(n==1)return 0;
if(n==2)return 1;
if(tmp[n]!=0)return tmp[n];
return tmp[n]=f(n-1)+f(n-2);
}如果tmp[n]不是0
代表已經有值了
則直接回傳 複雜度O(1)
費事數列
今天如果我們把重複的東西用一個陣列記下來
每次要用到的時候就可以直接取值
int tmp[1000005];
int f(int n){
if(n==1)return 0;
if(n==2)return 1;
if(tmp[n]!=0)return tmp[n];
return tmp[n]=f(n-1)+f(n-2);
}如果tmp[n]不是0
代表已經有值了
則直接回傳 複雜度O(1)
題目
k402
#include<bits/stdc++.h>
#define int long long
using namespace std;
int tmp[1000005];
int f(int n){
if(n==1)return 0;
if(n==2)return 1;
if(tmp[n]!=0)return tmp[n];
return tmp[n]=f(n-1)+f(n-2);
}
signed main(){
int a;
cin>>a;
cout<<f(a);
}要注意數字範圍(雖然他沒寫)
快速冪
快速冪
要怎麼計算出
a^b
int f(int a,int b){
int ans=1;
for(int i=1;i<=b;i++){
ans*=a;
}
return ans;
}簡單啊
a*a*a*a....總共*b次
時間複雜度:
O(n)
快速冪
太慢了
用快速冪
a^b=a^{b/2}*a^{b/2}
用一點數學理解
如果今天b是偶數
a^b=a*a^{b/2}*a^{b/2}
如果今天b是奇數
快速冪
用程式碼來寫的話
int f(int a,int b){
if(b==0)return 1;
int ans=0;
if(b%2==1)ans=a*f(a,b/2)*f(a,b/2);
else ans=f(a,b/2)*f(a,b/2);
return ans;
}a^0=1
a^b=a*a^{b/2}*a^{b/2}
a^b=a^{b/2}*a^{b/2}
b=0
b為奇數
b為偶數
快速冪
f(a,b)
f(a,b/2) f(a,b/2)
f(a,(b/2)/2) f(a,(b/2)/2)
f(a,(b/2)/2) f(a,(b/2)/2)
.
.
.
.
這樣似乎沒有簡化和加速
反而還讓他更慢
我們可以怎麼優化呢?
快速冪
f(a,b)
f(a,b/2) f(a,b/2)
f(a,(b/2)/2) f(a,(b/2)/2)
f(a,(b/2)/2) f(a,(b/2)/2)
.
.
.
.
左邊和右邊好像長一模一樣
那我們就做一次遞迴然後把答案記下來就行
快速冪
int f(int a,int b){
if(b==0)return 1;
int ans=0;
int half=f(a,b/2);
if(b%2==1)ans=a*half*half;
else ans=half*half;
return ans;
}每次做一次f(a,b/2)
這樣做出來會長怎樣
快速冪
f(a,b)
f(a,b/2) f(a,b/2)
f(a,(b/2)/2) f(a,(b/2)/2)
f(a,(b/2)/2) f(a,(b/2)/2)
.
.
.
.
最後只剩下最左邊這條分支
複雜度分析
有點像二分搜
只有一條分支
所以看他做幾層 就會有幾個操作
每次二分 所以層數=可以二分幾次
2^k=n
k=log\ n
複雜度:
O(log\ n)
題目
#include<bits/stdc++.h>
#define int unsigned long long
using namespace std;
const int mod=1e9+7;
int f(int a,int b){
if(b==0)return 1;
int ans=0;
int half=f(a,b/2)%mod;
if(b%2==1)ans=(a*half)%mod*half;
else ans=half*half;
return ans%mod;
}
signed main(){
int n;cin>>n;
for(int i=0;i<n;i++){
int a,b;cin>>a>>b;
cout<<f(a,b)<<'\n';
}
}
河內塔
河內塔
資工人一生必定會搬的一座塔
小時候玩具常有
以前APCS觀念題會考
河內塔(Hanoi Tower)
今天有ABC三根柱子
一開始A柱有n個盤子
下到上 由 大排到小
求最小步驟數
一次移動一個盤子
且小的不能在大的下面
河內塔(Hanoi Tower)
要怎麼用程式語言計算呢?
想法:
如果今天要從A移動第n個盤子到C
盤子由上到下 編號1~n
是不是要把1~n-1先移到B
n
1~n-1
1~n-1
n
1~n-1
A B C
河內塔(Hanoi Tower)
f(x)=f(x-1)+f(1)+f(x-1)
f(1)=1
遞迴式出來了
int f(int x){
if(x==1)return 1;
return f(x-1)*2+1;
}步驟數出來了
但題目通常都會問你怎麼搬
河內塔(Hanoi Tower)
我們要相信第回下去後做的是對的
將n號盤移到C之後就變成n-1個盤子的問題了
那我們假設把x盤子從A移到C 藉由B
f(x,A,C,B)
河內塔(Hanoi Tower)
void f(int x,char from,char to,char mid){
if(x==1){
cout<<"Move disc "<<x<<" from "<<from<<" to "<<to<<"\n";
return;
}
f(x-1,from,mid,to);
cout<<"Move disc "<<x<<" from "<<from<<" to "<<to<<"\n";
f(x-1,mid,to,from);
}只有一個盤子 直接移
先把x-1移到B
把x移到C
再把x-1移到C
我們要相信遞迴下去
程式會做好一切
題目
#include<bits/stdc++.h>
using namespace std;
int h(int x){
if(x==1)return 1;
return h(x-1)*2+1;
}
void f(int x,char from,char to,char mid){
if(x==1){
cout<<from<<' '<<to<<'\n';
return;
}
f(x-1,from,mid,to);
cout<<from<<' '<<to<<'\n';
f(x-1,mid,to,from);
}
int main(){
int n;cin>>n;
cout<<h(n)<<'\n';
f(n,'1','3','2');
}
題目
#include<bits/stdc++.h>
using namespace std;
int f(int x){
if(x>=101)return x-10;
//cout<<x<<' ';
return f(f(x+11));
}
int main(){
int n;
while(cin>>n && n!=0){
cout<<"f91("<<n<<") = "<<f(n)<<'\n';
}
}#include<bits/stdc++.h>
using namespace std;
#define int long long
int p[100000005];
int cut(int l,int r){
if(r==l+1)return 0;
int k=-1;
double mid=(p[l]+p[r])/2.0,mn=1e11;
for(int i=l+1;i<r;i++){
if(abs(p[i]-mid)<mn){
k=i;
mn=abs(p[i]-mid);
}
}
return cut(l,k)+cut(k,r)+p[r]-p[l];
}
signed main(){
int n,l;
cin>>n>>l;
for(int i=1;i<=n;i++){
cin>>p[i];
}
p[0]=0;
p[n+1]=l;
cout<<cut(0,n+1)<<'\n';
}d188
#include<bits/stdc++.h>
using namespace std;
int ans[3];
bool solve(int remain,int id){
int l=0,u=sqrt(remain);
if(id==2){
int t=sqrt(remain);
if(t-sqrt(remain)==0){
ans[id]=t;
return true;
}
return false;
}
else if(id==1)l=ans[id-1],u=sqrt(remain);
for(int n=l;n<=u;n++){
ans[id]=n;
if(solve(remain-n*n,id+1))return true;
}
return false;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
int n;
cin>>n;
while(n--){
int a;
cin>>a;
if(solve(a,0))cout<<ans[0]<<' '<<ans[1]<<' '<<ans[2]<<'\n';
else cout<<-1<<'\n';
}
}其實這題比較枚舉
dfs的感覺
遞迴
By wuchanghualeo
