基本算法

INDEX

  • 枚舉
  • 分治
  • 貪心

前言

如何解題?

看到一個題目我們要怎麼解?

要怎麼想出怎麼解?

有幾個思考步驟可以循序漸進地找到

前言

1.觀察性質

2.分析結論

3.提出做法

4.評估現有作法 (如果不夠好 回到1.)

5.實作

6.如果實測不夠好 (回到1.)

跟科學方法有點像

這個步驟很重要

不要看到不會寫的題目就放棄

前言

有時候確實需要神來一筆(通靈)

但

大多數情況會仰賴既有的經驗

(by 資訊之芽)

不斷累積經驗 這些就會習慣了

枚舉

枚舉

把每一種狀況都列出來

暴力

可以畫樹狀圖

利用遞迴來畫樹狀圖

有回溯的感覺

跟dfs有點像

枚舉

小明衣櫃有3種襪子、4種褲子、2種衣服

小明有幾種穿法

國中排列組合問題

想法:

畫樹狀圖

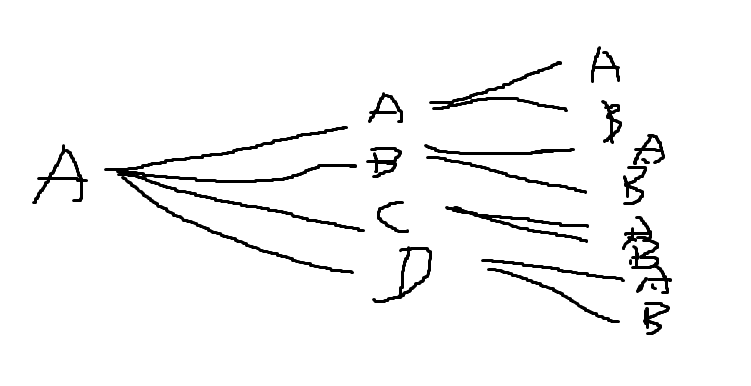
枚舉

優點:

不遺漏所有情形

暴力

很好實作 也很好想(根本不需要)

缺點:

太耗時間(TLE)

通常只能拿子題分

例題

zj b565

這題好長

題目不知道在講什麼

在看的時候要看出題目實際上想考甚麼

ZJ b565

最大連續和

題目想要求的其實就是

那要怎麼觀察呢

用枚舉的思維想的話

我們要把所有連續區間都枚舉出來

然後把裡面的值加起來

看哪個最大

ZJ b565

那要怎麼實作呢

先把每個連續區間列出來

假如今天有n=5

區間:

1~1, 1~2, 1~3, 1~4, 1~5

2~2, 2~3, 2~4, 2~5

3~3, 3~4, 3~5

4~4, 4~5

5~5

應該會找規律吧

實作看看?

ZJ b565

#include<bits/stdc++.h>
using namespace std;
int mx,arr[55];
int main(){
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++)cin>>arr[i];

        for(int i=1;i<=n;i++){
            int sum=0;
            for(int j=i;j<=n;j++){
                for(int k=i;k<=j;k++){
                    sum+=arr[k];
                }
                mx=max(sum,mx);
                sum=0;
            }
        }
        cout<<mx<<'\n';
        mx=0;
    }
}

來看一下這個方法如何?

想法:

用i,j枚舉所有區間

再用k把區間的值加起來

很笨? 這是我第一次寫這題用的想法

優化

想法:

我們在枚舉的時候j的迴圈是怎麼做的

是不是固定一個左界

接著用j不斷往後找

那i~j+1的區間是不是等於

(i~j)+(j+1)

同樣的區間一直被算到

發現性質不夠好(其實會過)

回去修正

優化

#include<bits/stdc++.h>
using namespace std;
int mx,arr[55];
int main(){
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++)cin>>arr[i];

        for(int i=1;i<=n;i++){
            int sum=0;
            for(int j=i;j<=n;j++){
                sum+=arr[j];
                mx=max(mx,sum);
            }
        }
        cout<<mx<<'\n';
        mx=0;
    }
}

少了一層迴圈

O(n^3)\ ->\ O(n^2)

優化

當然這題有更快的解法

不過現在先會枚舉的做法就行

從枚舉下手會發現事情解決了

接著再一步步拆解問題

優化解法

就會AC了

回溯

枚舉的另一種方法

更常考 但也更難

通常利用遞迴實作

但想法會了 啟發性蠻高的

一直往下走

遇到不能走return

回溯

透過一次次進入遞迴

建立出多層維度

樹狀圖

視覺化

概念會了 code也很好理解了

例題

p-1-7

很裸的題

p-1-7

子集合乘積

要怎麼做

有幾個子集合符合

那就把子集合全部列出來

再算有幾個符合就可以了

p-1-7

想法有了

接著要實作

要怎麼枚舉所有子集合

一樣用樹狀圖的想法

p-1-7

今天如果要建立一個子集合

裡面每種元素都只有兩種狀態

選 不選

1 1 2

假設選了第1跟第3

那是不是

1     1    2

選 不選 選

p-1-7

樹狀圖

p-1-7

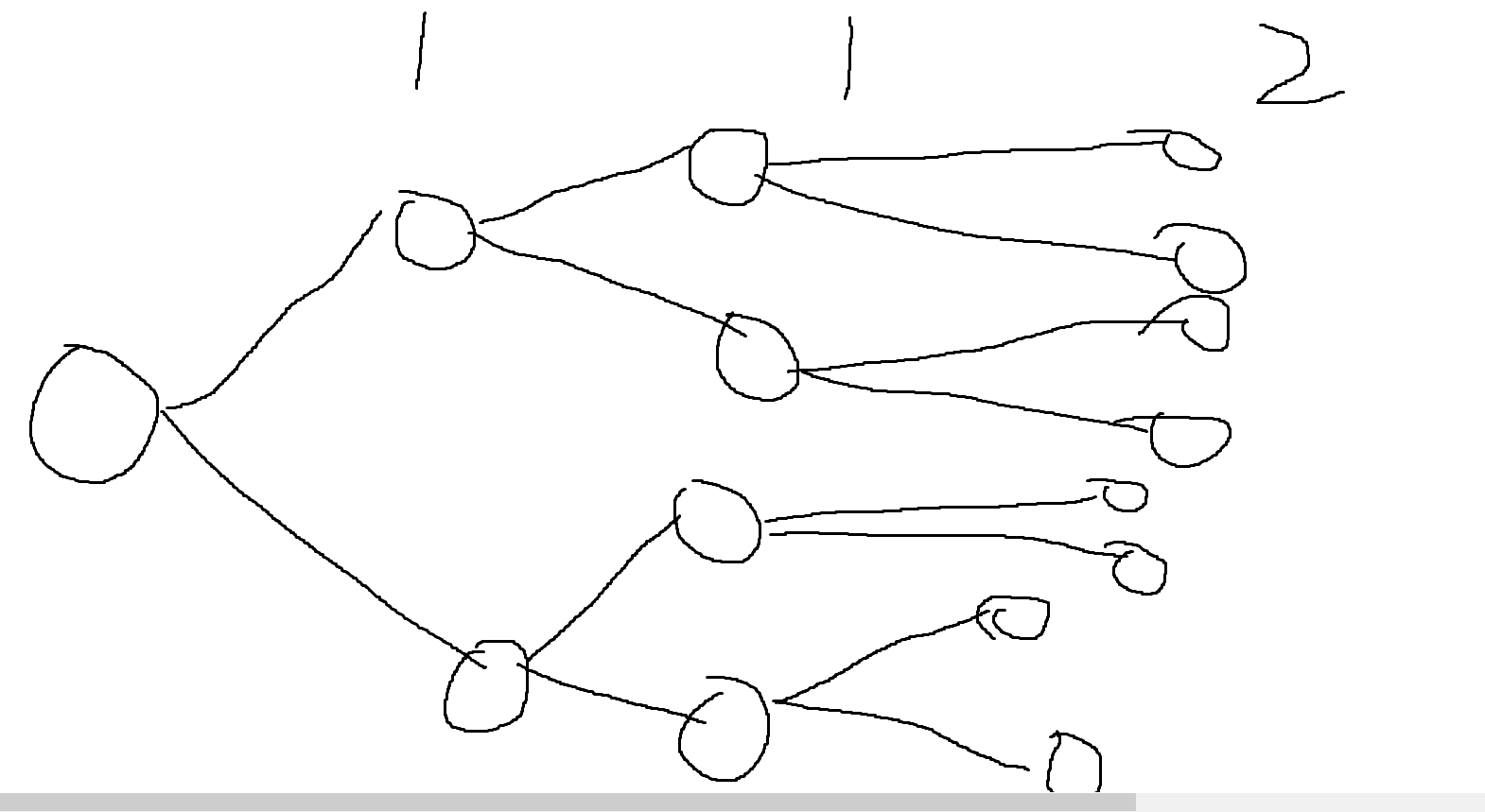
用樹狀圖可以表達所有子集合

接著實作樹狀圖

p-1-7

#include<bits/stdc++.h>
using namespace std;
vector<int>v;
int n,cnt;
void solve(int cur,int num){
    if(cur==n)return;
    int np=num*v[cur]%10009;
    if(np==1)cnt++;
    solve(cur+1,np);
    solve(cur+1,num);
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        int a;
        cin>>a;
        v.push_back(a);
    }
    solve(0,1);
    cout<<cnt;
}

solve(cur,num)

cur紀錄現在陣列的位置

num紀錄選到現在的值

每次進到下一格

分為兩種:

選:solve(cur,num*v[cur])

不選:solve(cur,num)

p-1-7

這題的做法

很多題其實都可以用到

但是在考試的時候要注意

測資範圍

如果太大就不能用(TLE)

O(2^n)

八皇后

八皇后

資工人一定下過的一盤棋

西洋棋皇后走法

要怎麼放才能讓棋盤上放8個皇后且不會互吃

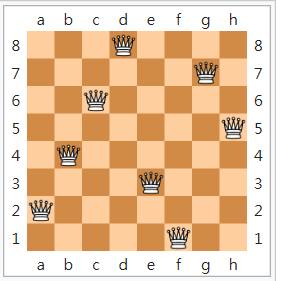
八皇后

方法一

每種格子有放跟不放

兩種可能

2^{64}

算不完的

TLE

來做點優化

八皇后

優化一:

每個橫排一定只能放一個

所以枚舉每一排放的位置

8^8

少了很多 但還是會TLE

八皇后

優化二:

今天從上排枚舉到下排

那我在枚舉的時候 是不是可以避開那些

已經被放過的列(colomn)

八皇后

優化三:

要怎麼快速檢查斜排呢

來觀察一下

(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4)
(3,1) (3,2) (3,3) (3,4)
(4,1) (4,2) (4,3) (4,4)

有兩種斜 / \

八皇后

(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4)
(3,1) (3,2) (3,3) (3,4)
(4,1) (4,2) (4,3) (4,4)

有沒有發現 同一條/的

x+y相同

先記好 等等判斷式會很多

八皇后

(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4)
(3,1) (3,2) (3,3) (3,4)
(4,1) (4,2) (4,3) (4,4)

有沒有發現 同一條\

x-y或y-x會相同

OK 你會快速檢查斜排了

八皇后

接下來就是實作了

void search(int cur){
	if(cur==n){
		tot++;
		return;
	}else{
		for(int i=0;i<n;i++){
			int ok=1;
			C[cur]=i;
			for(int j=0;j<cur;j++){
				if(C[cur]==C[j] || cur-C[cur]==j-C[j] || cur+C[cur]==j+C[j]){
					ok=0;
					break;
				}
			}
			if(ok){
				search(cur+1);
			}
		}
	}

}

直接上code

這應該是最難的部分

用0-base寫的

八皇后

if(cur==n){
  tot++;
  return;
}

cur是現在的排數

0~n-1排 所以枚舉到第n排時

代表前面成功放滿了棋盤

計數器++

跳出遞迴

八皇后

for(int i=0;i<n;i++){
  int ok=1;
  C[cur]=i;
  if(!ok)return;
  else search(cur+1);
}

先把一坨判斷式去掉

C陣列 紀錄棋子放在哪一格

C[3]=4 -> (3,4)

如果放了沒問題就繼續

否則跳出迴圈

八皇后

for(int j=0;j<cur;j++){
  if(C[cur]==C[j] || cur-C[cur]==j-C[j] || cur+C[cur]==j+C[j]){
    ok=0;
    break;
  }
}

迴圈:檢查從上面到這一排已沒有重複到

C[cur]=C[j]:放到同一列了

cur-C[cur]=j-C[j]:正斜向/

cur+C[cur]=j+C[j]:反斜向\

(x-y相同)

(x+y相同)

八皇后

#include<bits/stdc++.h>
using namespace std;
int n=8,tot,C[100];
void search(int cur){
	if(cur==n){
		tot++;
		return;
	}else{
		for(int i=0;i<n;i++){
			int ok=1;
			C[cur]=i;
			for(int j=0;j<cur;j++){
				if(C[cur]==C[j] || cur-C[cur]==j-C[j] || cur+C[cur]==j+C[j]){
					ok=0;
					break;
				}
			}
			if(ok){
				search(cur+1);
			}
		}
	}
}
int main(){
    search(0);
    cout<<tot<<'\n';
}

Code

答案出來應該是92

八皇后

題目

zj c104

c104

#include<bits/stdc++.h>
using namespace std;
int n=8,tot,arr[8][8],C[100],ans=0;
void search(int cur,int now){
	if(cur==n){
		tot++;
		ans=max(now,ans);
		return;
	}else{
		for(int i=0;i<n;i++){
			int ok=1;
			C[cur]=i;
			for(int j=0;j<cur;j++){
				if(C[cur]==C[j] || cur-C[cur]==j-C[j] || cur+C[cur]==j+C[j]){
					ok=0;
					break;
				}
			} 
			if(ok){
				search(cur+1,now+arr[cur][i]);
			}
		}
	}
	
}
int main(){
	int t;cin>>t;
	while(t--){
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++){
				cin>>arr[i][j];
			}
		}
		search(0,0);
		cout<<ans<<'\n';
		ans=0;
	}	
}

next_permutation

好用的工具

用來枚舉所有排列

可以用遞迴的 但手刻很累

do while少數有用的地方

next_permutation

next_permutation(begin,end);

一樣放記憶體位置

可以直接背用法

會把目標列迭代成下一個字典序，若已是最大字典序則回傳 false，因此一開始要sort

next_permutation

#include<bits/stdc++.h>
using namespace std;
#define int long long

vector<int> arr;
int n;
main(){
    cin>>n;
    for(int i=1;i<=n;++i){
        int a; cin>>a;
        arr.push_back(a);
    }
    sort(arr.begin(),arr.end());

    do{
        for(int i=0;i<n;++i) cout<<arr[i]<<' ';
        cout<<endl;
    }while(next_permutation(arr.begin(),arr.end()));
}

分治

分治

Divide & Conquer

分而治之

Divide:

切割問題

將大問題變成小問題

Conquer:

遞迴處理

用相似的方式解決小問題

最大連續和

b565

最大連續和

今天訂定一個函式f

f(l,r)

從l到r的最大連續和

所以今天如果我呼叫f(1,5)

它就能回傳給我1到5這個區間的最大連續和

最大連續和

今天訂定一個函式f

f(l,r)

從l到r的最大連續和

所以今天如果我呼叫f(1,5)

它就能回傳給我1到5這個區間的最大連續和

把它當作一個寫好的函式並相信它

最大連續和-分

分:

今天我們把陣列切一半

答案有幾種出現的方式?

分

1.全在左邊

2.全在右邊

分

3.跨越中間

問題切割完了

要怎麼治

最大連續和-治

治:

今天如果是1.2.

全部在左半邊或右半邊的

那是不是可以表示成

f(l,r) = f(l, mid)

f(l, r) = f(mid, r)

併在一起處理:

f(l, r) = max(f(l, mid), f(mid, r))

治

那3.呢?

我們可以把它分成左邊跟右邊

一直往左加 回傳最大值

一直往右加 回傳最大值

治

合併在一起

f(l, r) = max(f(l, mid), f(mid, r), crossmid)

還有一件重要的是

寫遞迴的時候一定要加

終止條件!

治

今天我們一直切割陣列

如果切到f(l,r) l==r的時候

只剩一個數 是不是最大連續和就是他自己

所以

if(l==r)return arr[l];

這就是本題的想法

接著是要花很多時間理解的code

CODE

#include<bits/stdc++.h>
#define maxn 105
using namespace std;
int arr[maxn];
int f(int l,int r){
    if(l==r)return arr[l];
    int mid=(l+r)/2;
    int ans=max(f(l,mid),f(mid+1,r));
    int mxl=0,mxr=0,L=0,R=0;
    for(int i=mid;i>=l;i--){
        L+=arr[i];
        mxl=max(mxl,L);
    }
    for(int i=mid+1;i<=r;i++){
        R+=arr[i];
        mxr=max(mxr,R);
    }
    ans=max(ans,mxl+mxr);
    return ans;
}
int main(){
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++)cin>>arr[i];
        cout<<f(1,n)<<'\n';
    }
}

這坨應該最難懂

CODE

if(l==r)return arr[l];
int mid=(l+r)/2;
int ans=max(f(l,mid),f(mid+1,r));

1:終止條件

2.繼續切割陣列算好兩邊的答案

在取max的時候 用f往下呼叫 等做完合併上來的時候

就可以得到答案

CODE

 int mxl=0,mxr=0,L=0,R=0;
 for(int i=mid;i>=l;i--){
   L+=arr[i];
   mxl=max(mxl,L);
 }
 for(int i=mid+1;i<=r;i++){
   R+=arr[i];
   mxr=max(mxr,R);
 }

mxl,mxr:紀錄從中間開始算的最大值

L,R:往左/右加的連續和

mxl+mxr=越過中間的最大連續和

複雜度?

每次都二分

應該蠻好算的

過程會比需要掃過陣列

複雜度:

O(n\ log\ n)

分治

分治的精隨:

跟遞迴的概念有點像

通常需要一點經驗

跟之後的dp概念有點像

一樣:

相信自己的遞迴下去是對的

它就會是對的

MergeSort

合併排序法

MergeSort

今天有一個函式f

f(l,r)

不會回傳值

單純幫你把 l-r區間排序好

如何分?如何治?

分

一樣把陣列切一半

呼叫f(l,mid) f(mid,r)

ok 那兩邊就各自排序好了

          3               8               2              7              4              1                               

治

接著 把兩邊合起來

          2              3               8              1              4              7                               

治

2  3  8

1  4  7

從第一項往後比

小的先丟進一個大陣列

1 2 3 4 7 8

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 1000005
int arr[maxn],n;
void mergesort(int l,int r){
    if(l==r)return;
    int mid=(l+r)/2;
    mergesort(l,mid);
    mergesort(mid+1,r);
    int n1=mid-l+1,n2=r-mid;
    int L[n1+5],R[n2+5];
    for(int i=0;i<n1;i++)L[i]=arr[l+i];
    for(int i=0;i<n2;i++)R[i]=arr[mid+i+1];
    int x=0,y=0,z=l;
    while(x<n1 && y<n2){
        if(L[x]<R[y]){
            arr[z++]=L[x++];
        }
        else arr[z++]=R[y++];
    }
    while(x<n1)arr[z++]=L[x++];
    while(y<n2)arr[z++]=R[y++];
}
main(){
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++)cin>>arr[i];
        mergesort(1,n);
        for(int i=1;i<=n;i++)cout<<arr[i]<<' ';
    }
}

這個code再叫我寫一次

我會死給你看

CODE

if(l==r)return;
int mid=(l+r)/2;
mergesort(l,mid);
mergesort(mid+1,r);

如果只剩一個數字 不用排序

呼叫將兩半陣列排好的函式

CODE

int n1=mid-l+1,n2=r-mid;
int L[n1+5],R[n2+5];
for(int i=0;i<n1;i++)L[i]=arr[l+i];
for(int i=0;i<n2;i++)R[i]=arr[mid+1+i];

L,R:陣列儲存左半右半

接著把東西裝進去變成兩半陣列

n1,n2:兩個切一半的長度

L:arr[l]~arr[mid]

R:arr[mid+1]~arr[r]

CODE

int x=0,y=0,z=l;
  while(x<n1 && y<n2){
    if(L[x]<R[y]){
      arr[z++]=L[x++];
    }
  else arr[z++]=R[y++];
}

x,y:維護現在是誰跟誰在比(類似指針)

z:把小的放入原陣列的位置

每次放完z++

如果放左邊的 x++

如果放右邊的 y++

CODE

while(x<n1)arr[z++]=L[x++];
while(y<n2)arr[z++]=R[y++];

比到最後應該會有人先放完

所以把另一個全部填在後面

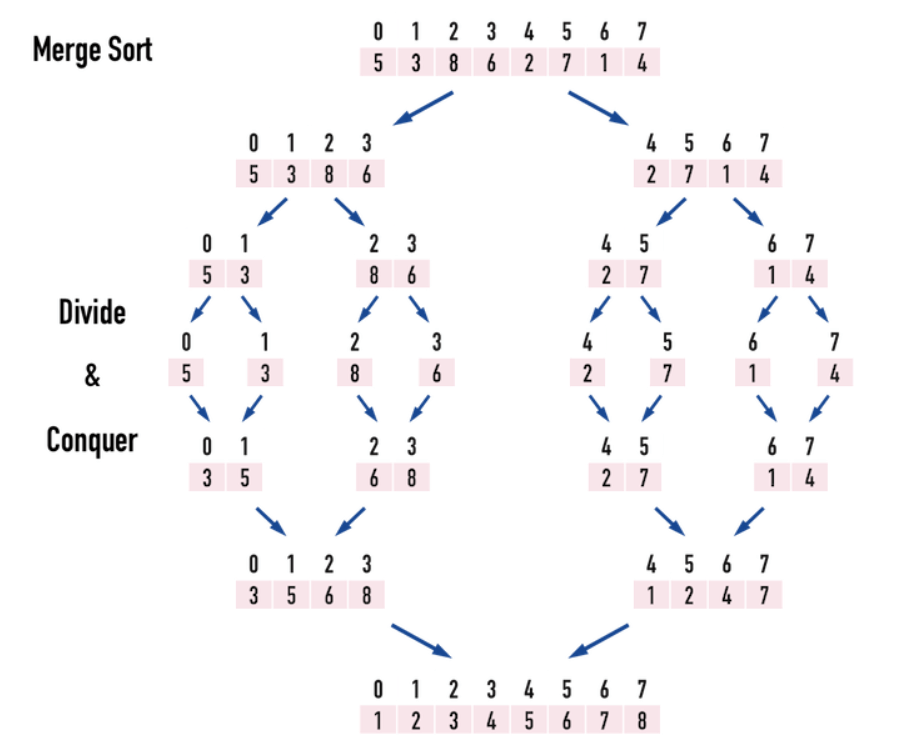
逆序數對

tioj 1080

逆序數對

排序是由小到大

所以今天如果

arr[i]>arr[j]

i<j

那(i,j)就是一組逆序數對

題目要算有幾組

逆序數對

今天一樣用一個函數f

f(l,r)

回傳逆序數對數量

接著分治

分

          3               8               2              7              4              1                               

用f(l,mid) f(mid+1,r)

求出兩邊的逆序數量

接著要求跨過兩邊的數對數量

治

          3               8               2              7              4              1                               

接著要排序

因為都計算完兩邊內部自己的了

所以排序並不會影響接下來所有計算

治

接著應該會覺得有點像剛剛的過程

2   3   8

1   4   7

我們會挑小的放到大陣列對吧

那如果今天放的是右邊的

是不是代表左邊全部都比它大

1  2  3  4  7  8

治

沒錯它就是用MergeSort計算

一邊sort 一邊合併一邊計算

先自己去實作吧

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 1000005
int arr[maxn],n,ans;
void mergesort(int l,int r){
    if(l==r)return;
    int mid=(l+r)/2;
    mergesort(l,mid);
    mergesort(mid+1,r);
    int n1=mid-l+1,n2=r-mid;
    int L[n1+5],R[n2+5];
    for(int i=0;i<n1;i++)L[i]=arr[l+i];
    for(int i=0;i<n2;i++)R[i]=arr[mid+i+1];
    int x=0,y=0,z=l;
    while(x<n1 && y<n2){
        if(L[x]<=R[y]){
            arr[z++]=L[x++];
        }
        else{
            ans+=n1-x;
            arr[z++]=R[y++];
        }
    }
    while(x<n1)arr[z++]=L[x++];
    while(y<n2)arr[z++]=R[y++];
}
signed main(){
    int n,c=1;
    while(cin>>n && n){
        for(int i=1;i<=n;i++)cin>>arr[i];
        mergesort(1,n);
        cout<<"Case #"<<c<<": "<<ans<<'\n';
        c++;
        ans=0;
    }
}

CODE

if(L[x]<=R[y]){
  arr[z++]=L[x++];
}
else{
  ans+=n1-x;
  arr[z++]=R[y++];
}

< 會讓逆序數對多算相同的 要改<=

如果右邊比較大

那答案就是左邊剩下的元素數量

OK 基本算法會先停在這邊

之後會先上dp

希望分治沒讓你燒雞

我自己去年是大燒雞啦

加油

基本算法

By wuchanghualeo

Made with Slides.com

基本算法

  • 50

More from wuchanghualeo