Dynamic Programming
動態規劃
INDEX
- 基本原理
- 簡單例題
- LIS
- LCS
- 背包問題
基本原理
基本原理
用表格紀錄programming
dp:用變動的表格來求解
比較像一種思考模式、手段
而不是演算法
基本概念
跟分治有點像
將問題分成子問題
接著合併、解決子問題
最後得到答案
基本概念
1.定義子問題
2.找到問題和子問題間的(遞迴)關係
3.找出計算的順序
並避免用遞迴計算
基本概念
要如何從子問題得到原本問題的答案?
首先子問題我們可以稱為狀態
看到題目的時候需要設計適合的狀態
接著要去想狀態間的關係(轉移方程)
ex:
A
B
+10
基本概念
接著依照順序
把問題解決
得到最後的答案
例題1 爬樓梯
有個小朋友要上樓梯
每次可以往上走1階或2階(往上)
有幾種可以到n階的方法
例題1 爬樓梯
首先
來設定狀態
我們設定dp[i]是走到第i格的方法數
因此最後要求的答案
要算出dp[n]的數值
例題1 爬樓梯
找出狀態間的關係
今天要走到第i階之前
要先走到i-1跟i-2階
因此dp[i]=dp[i-1]+dp[i-2]
例題1 爬樓梯
用遞迴式表示
發現在用遞迴的時候要相信呼叫完他會幫你算好
如果從小開始算的話?
一般人正常算費式數列應該都是這樣算的吧
其實就是費事數列
用到dp[i]時 dp[i-1],dp[i-2]的值已經算好了
例題1 爬樓梯
一開始要有個狀態
才能一直轉移上去
dp[1]=1;
dp[2]=2;
接著轉移
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
答案
cout<<dp[n]<<'\n';例題2 走格子
有一個m*n的表格
從左上角走到右下角
每一步只能往右或往下一格
有幾種走法
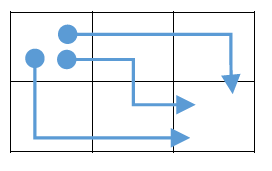
例題2
先定義子問題
dp[i][j]=走到(i,j)的方法數
接著是轉移式
由於只能往右或往下走
所以當i>1 && j>1的時候
這一格可以從上面或左邊走過來
答案:dp[n][m]
例題2
初始狀態
要把所有沒有上面或左邊的先手算完
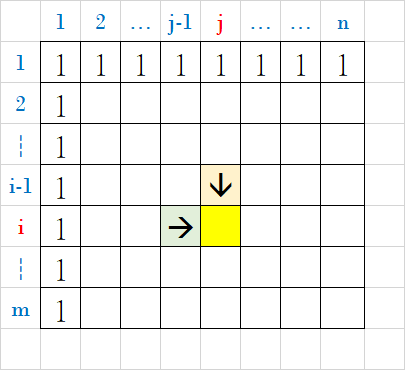
也就是這兩排
而這兩排都只有一條路
所以都是1
這是轉移的方式
方法數是從上面和左邊走下來的總和
例題2
初始狀態
for(int i=1;i<=n;i++)dp[i][1]=1;
for(int i=1;i<=m;i++)dp[1][i]=1;轉移式
for(int i=2;i<=n;i++){
for(int j=2;j<=m;j++){
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}答案
cout<<dp[n][m]<<'\n';這幾題讓你們稍微感受一點點
dp的感覺
後面的題目會一步步建立起dp的思維模式
簡單例題
例題1 爬樓梯最小成本
跟一開始的費事數列有點像?
看到dp題目要怎麼開始想
狀態!
今天定義dp[i]是走到第i格最小成本
答案:dp[n]
要怎麼轉移?
例題1 爬樓梯最小成本
轉移式!
今天我在第i格
我能從我下面一格或兩格走來
那既然dp[i]是第i格的最小
dp[i-1],dp[i-2]就是i-1,i-2格的最小
那今天我們要接著走的應該要選小的繼續走
所以轉移式就出來了!
例題1 爬樓梯最小成本
轉移式!
dp[i]=min(dp[i-1],dp[i-2])+cost[i];選小的(取min)、繼續走(+這格成本)
初始狀態
走第1格只有1個成本->cost[1]
走第2格 也能只有1個成本->cost[2]
dp[1]=cost[1];
dp[2]=cost[2];答案
cout<<dp[n]<<'\n';例題1 爬樓梯最小成本
每次轉移:O(1)
n次:O(n)
時間複雜度:
#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int dp[maxn],cost[maxn];
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>cost[i];
dp[1]=cost[1];
dp[2]=cost[2];
for(int i=3;i<=n;i++){
dp[i]=min(dp[i-1],dp[i-2])+cost[i];
}
cout<<dp[n]<<'\n';
}
把上面題目刷完就能高中競程輕鬆一半
這個裸題蠻多的
都寫
dp多刷題就能比較抓得住感覺
基本每次北市賽、TOI、APCS基本都會考
例題2 frog1
每次可以1格或2格
但花費|h[i]-h[j]|
狀態!
dp[i]=跳到第i格最小花費
答案:dp[n]
接著要想轉移式
例題2 frog1
轉移式!
跟上一題想法差不多
要找前兩個中最小
但是要考慮他們的高度
因為跳過來也有花費
dp[i]=min(從前一格跳過來,從前兩格跳過來)
例題2 frog1
轉移式!
for(int i=3;i<=n;i++){
dp[i]=min(dp[i-1]+abs(h[i-1]-h[i]),dp[i-2]+abs(h[i-2]-h[i]));
}初始狀態
(dp[1]=0;)
dp[2]=abs(h[2]-h[1]);答案
cout<<dp[n]<<'\n';例題2 frog2
最多走k格
這題的想法應該不難
就使原本的2個轉移變成k個
狀態一樣
來想轉移式
轉移式
今天可以從前k個跳過來
那我希望走的就是最小的路徑
取min 然後算跳過來的成本
for(int i=k+1;i<=n;i++){
for(int j=1;j<=k;j++){
dp[i]=min(dp[i],dp[i-j]+abs(h[i]-h[i-j]));
}
}每次都取一次min
看從哪一格成本比較低
例題2 frog2
初始狀態!
因為我們會用到前k個
所以要先手算好1~k
那1~k都可以1次跳
dp[i]=從第1格跳過來的成本
for(int i=1;i<=k;i++)dp[i]=abs(h[i]-h[1]);例題2 frog2
CODE
#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int dp[maxn],h[maxn];
int main(){
fill(dp,dp+maxn,1e9);
int n,k;cin>>n>>k;
for(int i=1;i<=n;i++)cin>>h[i];
for(int i=1;i<=k;i++)dp[i]=abs(h[i]-h[1]);
for(int i=k+1;i<=n;i++){
for(int j=1;j<=k;j++){
dp[i]=min(dp[i],dp[i-j]+abs(h[i]-h[i-j]));
}
}
cout<<dp[n]<<'\n';
}
由於每次都取min
如果預設為0
全部都會是0
例題2 frog2
題目
p-6-6
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
int g[205][205],dp[205][205];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>g[i][j];
}
}
dp[1][1]=g[1][1];
for(int i=1;i<=n;i++)dp[i][1]=dp[i-1][1]+g[i][1];
for(int i=1;i<=m;i++)dp[1][i]=dp[1][i-1]+g[1][i];
for(int i=2;i<=n;i++){
for(int j=2;j<=m;j++){
dp[i][j]=max(dp[i][j-1],dp[i-1][j])+g[i][j];
}
}
cout<<dp[n][m];
}p-6-2
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int s[200005],dp[200005];
for(int i=1;i<=n;i++){
cin>>s[i];
}
dp[1]=s[1];
dp[2]=max(dp[1],s[2]);
for(int i=3;i<=n;i++){
dp[i]=max(dp[i-1],dp[i-2]+s[i]);
}
cout<<dp[n];
}p-6-3
#include<bits/stdc++.h>
using namespace std;
#define int long long
int32_t main(){
int n;
cin>>n;
int c[100005],dp[100005];
for(int i=1;i<=n;i++){
cin>>c[i];
}
dp[1]=c[1];
dp[2]=c[2];
dp[3]=c[3]+min(c[1],c[2]);
for(int i=4;i<=n;i++){
dp[i]=c[i]+min({dp[i-1],dp[i-2],dp[i-3]});
}
if(n!=1)cout<<min(dp[n],dp[n-1]);
else cout<<c[1];
}p-6-4
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,t,dp[2][200005];
cin>>n>>t;
vector<pair<int,int>>v;
v.push_back({0,0});
for(int i=0;i<n;i++){
int a,b;
cin>>a>>b;
v.push_back({a,b});
}
dp[0][1]=(abs(t-v[1].first));
dp[1][1]=(abs(t-v[1].second));
for(int i=2;i<=n;i++){
dp[0][i]=min(dp[0][i-1]+abs(v[i-1].first-v[i].first),dp[1][i-1]+abs(v[i-1].second-v[i].first));
dp[1][i]=min(dp[0][i-1]+abs(v[i-1].first-v[i].second),dp[1][i-1]+abs(v[i-1].second-v[i].second));
}
cout<<min(dp[0][n],dp[1][n])<<'\n';
}LIS
LIS?
LIS
Longest increasing subsequence
最長遞增子序列
子序列:之前枚舉有講過
取跟不取的那題
要找數列中
最長且符合遞增的子序列
LIS
舉例:
1 3 5 2 9
3 9
遞增子序列
1 5 2 9
不是遞增子序列
要找出最長的(可能不只一個)
LIS
1 3 5 2 9
其中一種最長的:1 3 5 9
接下來要用dp的想法來解
有兩種做法
LIS
設定狀態
dp[i]是以第i項作為結尾的最長子序列長度
答案:dp[1~n]中最長的
接著要來想轉移式
每次都掃過前面的看能不能接
只求長度
LIS
由於前面dp[j]存的都是最長的子序列長度
每次往前找到如果比現在位置的值小就接看看
看怎麼接長度最長
for(int i=2;i<=n;i++){
for(int j=1;j<i;j++){
if(arr[i]>arr[j]){
dp[i]=max(dp[i],dp[j]+1);
}
}
}j每次往前掃
遇到可以接的 看看接上去會不會比原本大
CODE
#include<bits/stdc++.h>
#define maxn 200005
using namespace std;
int arr[maxn],dp[maxn];
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>arr[i];
fill(dp,dp+maxn,1);
for(int i=2;i<=n;i++){
for(int j=1;j<i;j++){
if(arr[i]>arr[j]){
dp[i]=max(dp[i],dp[j]+1);
}
}
}
int ans=1;
for(int i=1;i<=n;i++)ans=max(ans,dp[i]);
cout<<ans<<'\n';
}
LIS
複雜度:
很遺憾
這個方式過不了這一題的
看一下測資
2e5->n log n
接著用一點特殊的算法
LIS
Robinson–Schensted–Knuth algorithm
用的是貪心想法
直接來看怎麼做
利用binary search加速
如果聽不懂可以看這個
LIS
今天我們要來做一個LIS
如果a比陣列所有值大
那我們就可以放在最後
長度+1
要放入一個數字a
否則找一個它應該在的位置
將原有值替換掉
LIS
要放入一個數字2
ex
1 3 5 2 9
1 3 5
假如目前LIS做到第3
它沒比5大
找到適合它的位置
->把3換掉
LIS:1 2 5
LIS
要放入一個數字9
ex
1 3 5 2 9
1 2 5
接著LIS做到第4
它比5大
推到最後
LIS:1 2 5 9
長度=4
LIS
由於是遞增序列
是不是就有單調性
所以在找要怎麼替換的時候
可以快速找到
二分搜!
問題瞬間變簡單很多
LIS
CODE
#include<bits/stdc++.h>
#define maxn 200005
using namespace std;
int arr[maxn],dp[maxn];
vector<int>v;
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++){
cin>>arr[i];
}
for(int i=1;i<=n;i++){
if(lower_bound(v.begin(),v.end(),arr[i])==v.end())v.push_back(arr[i]);
else{
auto it=lower_bound(v.begin(),v.end(),arr[i]);
*it=arr[i];
}
}
cout<<v.size();
}利用二分搜
要注意 題目是嚴格遞增
複雜度:O(n log n)
LIS
最後vector裡面的並不是真正的LIS
要利用pos[]陣列來存
再用特殊的找法
詳情上面的連結有
題目
LCS
LCS
求最長共同子序列長度
並找一種輸出
ex
s1 : 5 7 9 3 1 2
s2 : 3 5 3 2 8
LCS=5 3 2
先來講長度
LCS
狀態
dp[i][j]=s1前i個跟s2前j個的LCS長度
答案=dp[n][m]
接著要來想轉移式
LCS
考慮兩種情況
1. s1[i]==s2[j]
2. s1[i]!=s2[j]
LCS長度是上面跟左邊格的mx
dp[i][j]=max(dp[i-1][j],dp[i][j-1])
則LCS長度+1
dp[i][j]=dp[i-1][j-1]+1
LCS
長度求完了 要怎麼找子序列
要來找怎麼轉移過來的
如果dp[i][j]是由dp[i-1][j-1]轉移過來的
代表s[i]==s[j]
用反推的
然後記錄怎麼來的
LCS
用一個pre陣列存起來
0 1 2分別是三種轉過來的路徑左上 左 上
最後用遞迴走回去並輸出
直接看code
CODE
#include<bits/stdc++.h>
#define maxn 1005
using namespace std;
int dp[maxn][maxn],pre[maxn][maxn];
vector<int>s1,s2;
void print(int i,int j){
if(i==0 || j==0)return;
if(pre[i][j]==1){
print(i-1,j-1);
cout<<s1[i]<<' ';
}
else if(!pre[i][j]){
print(i,j-1);
}
else print(i-1,j);
return;
}
int main(){
int n,m;cin>>n>>m;
s1.push_back(0);
s2.push_back(0);
for(int i=0;i<n;i++){
int a;cin>>a;
s1.push_back(a);
}
for(int i=0;i<m;i++){
int a;cin>>a;
s2.push_back(a);
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(s1[i]==s2[j]){
dp[i][j]=dp[i-1][j-1]+1;
pre[i][j]=1;
}
else{
if(dp[i][j-1]>dp[i-1][j]){
dp[i][j]=dp[i][j-1];
pre[i][j]=0;
}
else{
dp[i][j]=dp[i-1][j];
pre[i][j]=2;
}
}
}
}
cout<<dp[n][m]<<'\n';
print(n,m);
}Dynamic Programming
By wuchanghualeo
Dynamic Programming
- 63



