Calculus
微積分
— 吳若喬
目錄
微積分
主要包括微分學和積分學兩個部分,是研究極限、微分、積分和無窮級數等的一個數學分支。更本質的講,微積分學是一門研究連續變化的學問。
它使得函數、速度、加速度和斜率等均可用一套通用的符號進行演繹。
-選錄自維基百科

前導知識
實數
微積分研究的對象是函數的變化,涉及的數字皆是實數。
1
無窮大
以質數和無限旅館悖論作解釋。
(先來凍凍腦)
2
趨勢
極限的前導概念。
3
無窮多?有限?
質數
無窮多?有限?
質數
歐幾里德證明法:
假設有限質數的集合=p1,p2,p3,...,p6
P=此集合的數相乘,q=P+1 (q可為質數或非質數)
無窮多?有限?
質數
歐幾里德證明法:
假設有限質數的集合=p1,p2,p3,...,p6
P=此集合的數相乘,q=P+1 (q可為質數或非質數)
1.假設q為質數
無窮多?有限?
質數
歐幾里德證明法:
假設有限質數的集合=p1,p2,p3,...,p6
P=此集合的數相乘,q=P+1 (q可為質數或非質數)
1.假設q為質數
=>至少有一個質數不存在於有限質數集合當中
無窮多?有限?
質數
歐幾里德證明法:
假設有限質數的集合=p1,p2,p3,...,p6
P=此集合的數相乘,q=P+1 (q可為質數或非質數)
2.假設q為非質數
無窮多?有限?
質數
歐幾里德證明法:
假設有限質數的集合=p1,p2,p3,...,p6
P=此集合的數相乘,q=P+1 (q可為質數或非質數)
2.假設q為非質數
即存在一個質數因子k可整除q
無窮多?有限?
質數
歐幾里德證明:
假設有限質數的集合=p1,p2,p3,...,p6
P=此集合的數相乘,q=P+1 (q可為質數或非質數)
2.假設q為非質數
即存在一個質數因子k可整除q
假設此質數因子k在有限質數的集合中:
k必整除P,但同時整除q,代表k可整除P、q之差(P+1-P=1)
但是質數皆無法整除1,即k無法同時整除P、q
因此k不在此有限集合p1,p2,p3,...,p6當中
無限旅館悖論
太長了啦放在hackmd
趨勢
請判斷以下的函數為發散還是收斂?
- 第一
- 第二
- 2u4n0
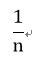
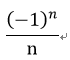
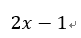
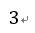
函數
請判斷以下的函數為發散還是收斂?
- 第一
- 第二
- 2u4n0
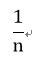
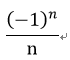
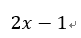
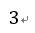
收斂
函數
請判斷以下的函數為發散還是收斂?
- 第一
- 第二
- 2u4n0
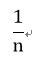
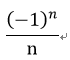
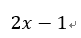
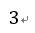
收斂
函數
請判斷以下的函數為發散還是收斂?
- 第一
- 第二
- 2u4n0
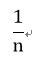
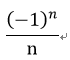
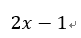
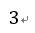
發散
函數
請判斷以下的函數為發散還是收斂?
- 第一
- 第二
- 2u4n0
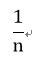
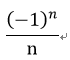
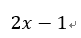
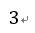
收斂
Definition
發散:
當n越來越大,數列不會趨近一定數
收斂:
當n越來越大,數列會趨近於或等於某一定數。
而這個數列所趨近的數為L,稱之為該數列的極限
數學上定義的符號為
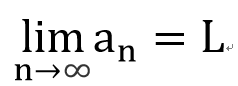
- 第一
- 第二
- 2u4n0
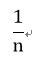
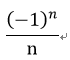
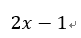
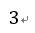
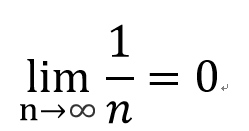
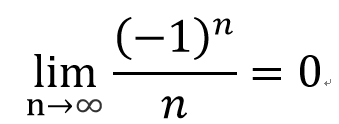
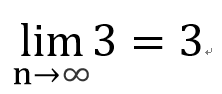
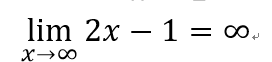
〞
切線是割線的極限。
〞
limit?


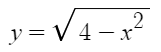
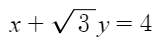
圓:
直線:

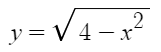
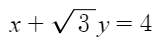
圓:
直線:
P
Q

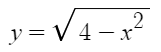
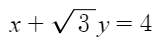
圓:
直線:
P
Q

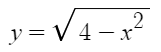
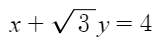
圓:
直線:
P
Q

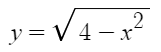
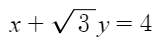
圓:
直線:
P
Q

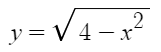
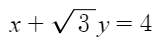
圓:
直線:
P
Q
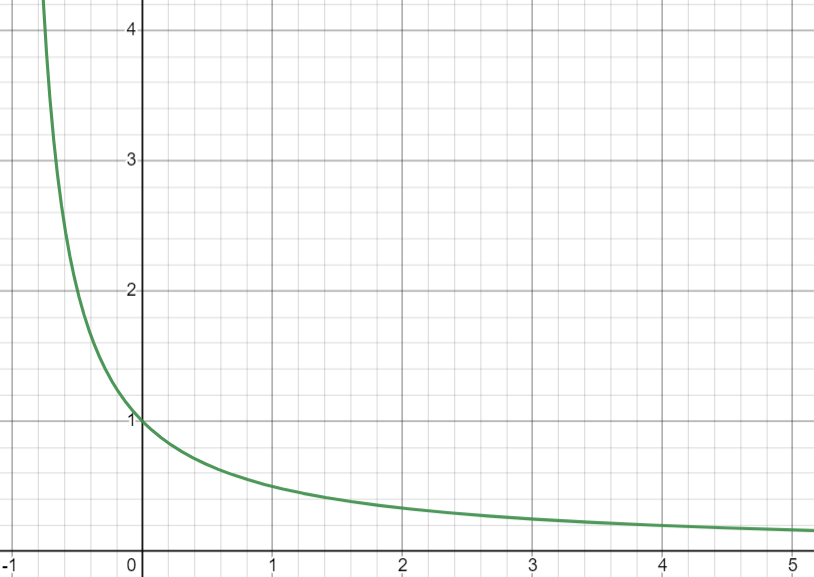
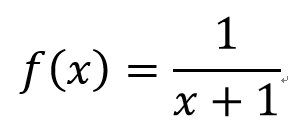
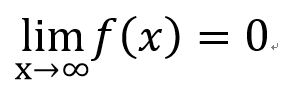

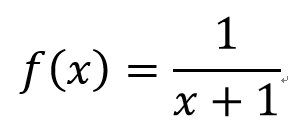
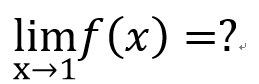

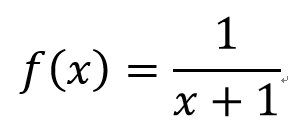
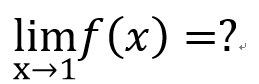

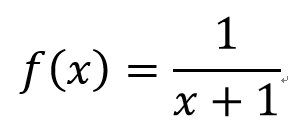
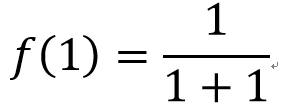
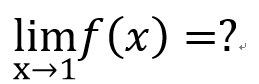

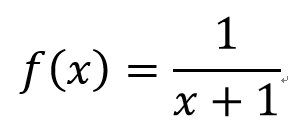
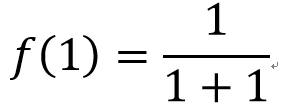
無關
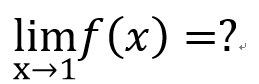

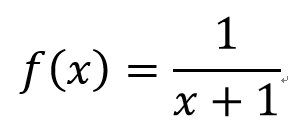
1/2
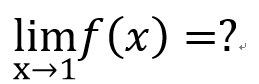

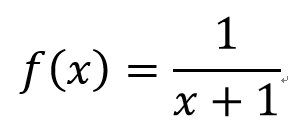
1/2
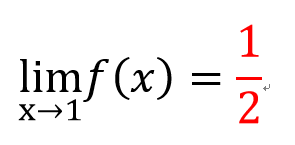

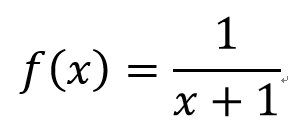
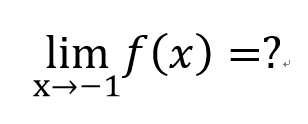
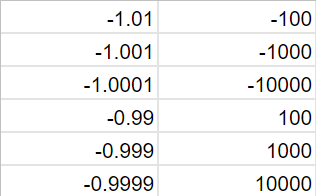

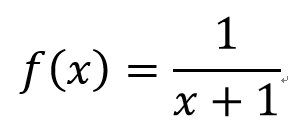
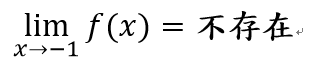
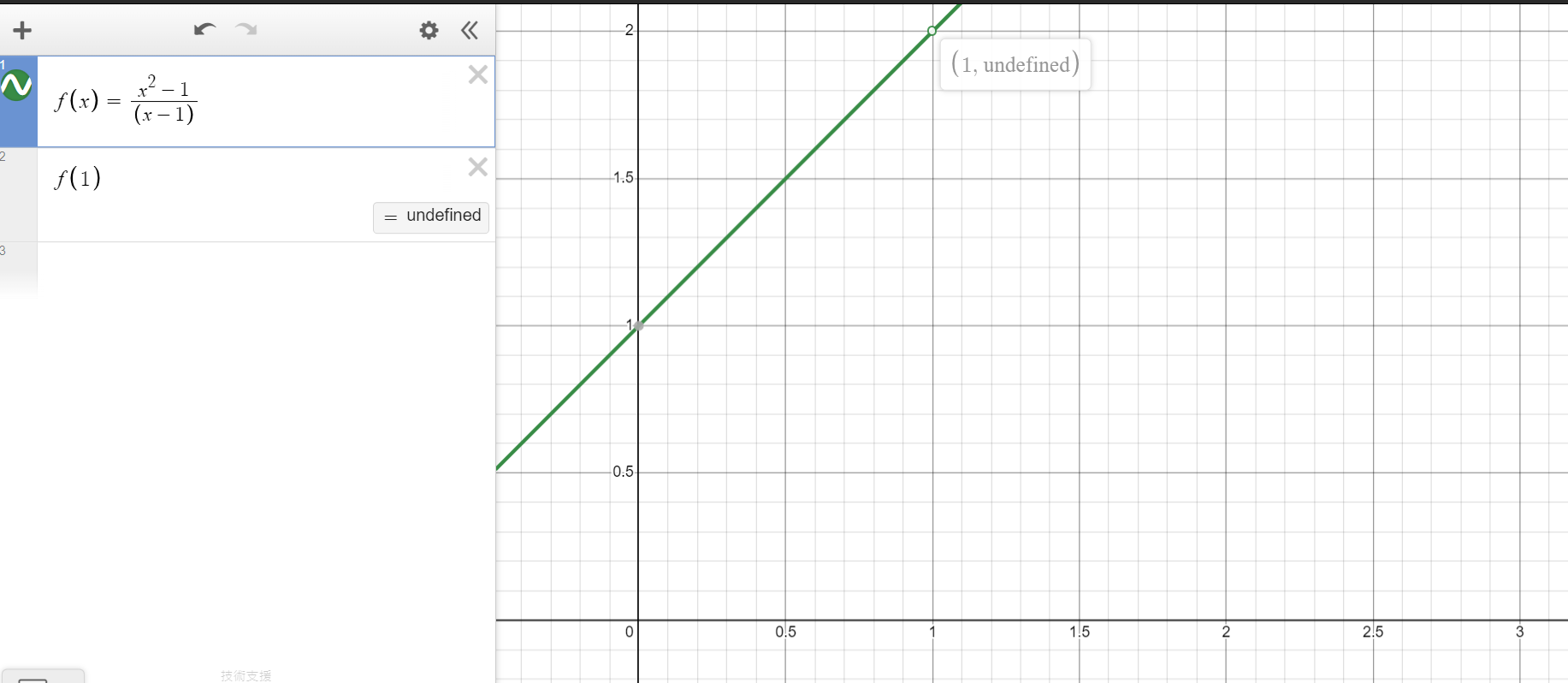
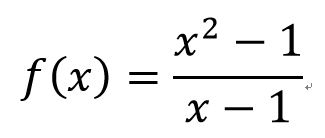

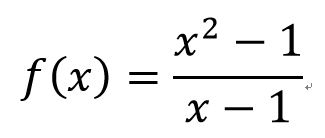

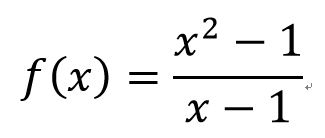
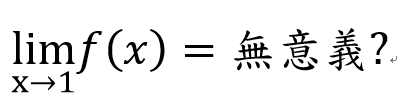
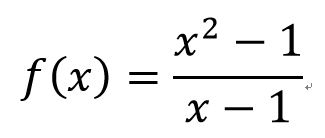
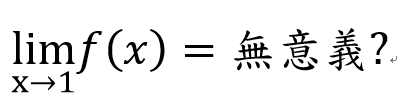
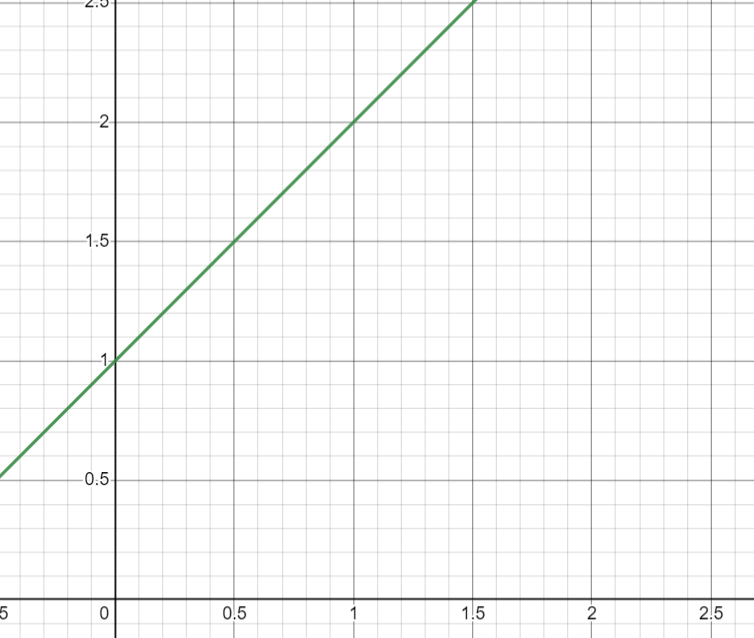
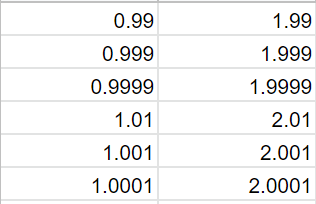
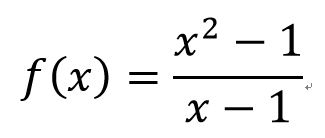

=
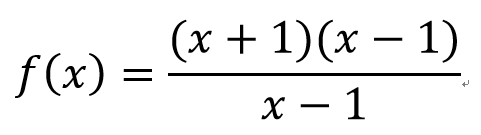
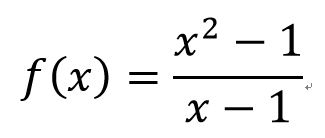

=
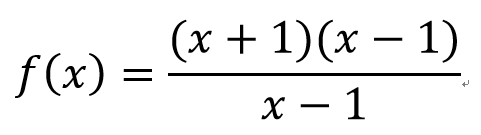
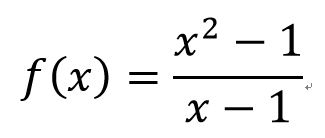

=
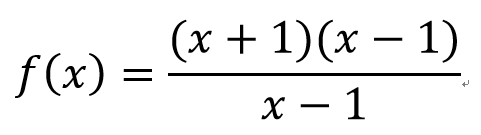
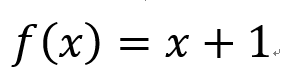
=
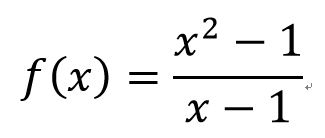

=
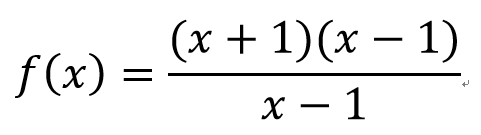
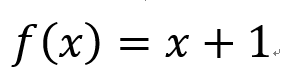
=
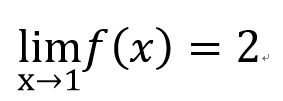
一些長得很怪的東西
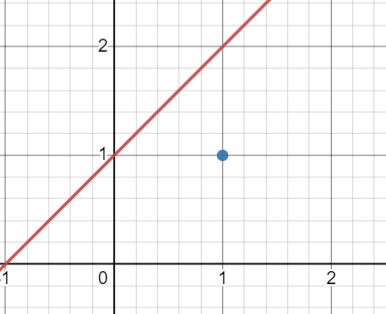
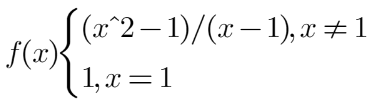
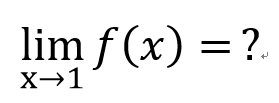
一些長得很怪的東西

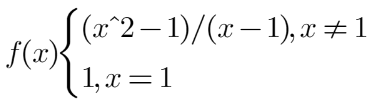
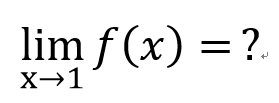
一些長得很怪的東西

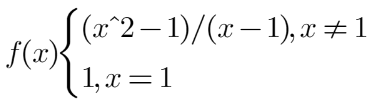
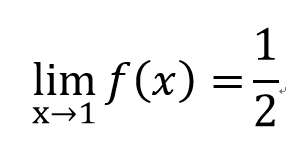
小總結
1.一次函數和多項式
函數值=極限值
2.若f(x)中x≠a的條件和h(x)中x≠a的條件相同
則f(x)和h(x)在x趨近於a時相等
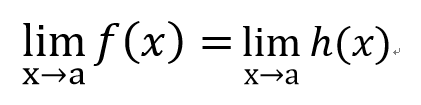
左極限和右極限
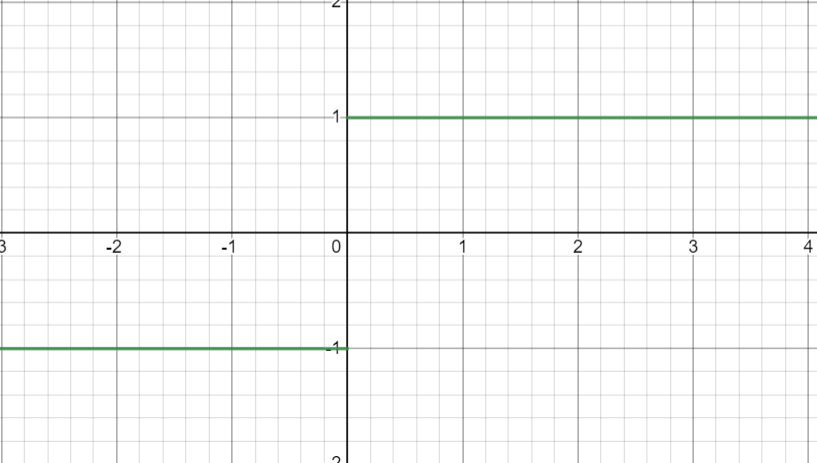
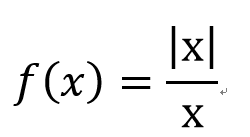

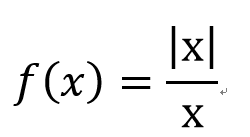
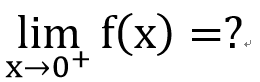
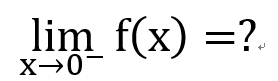
右極限
左極限

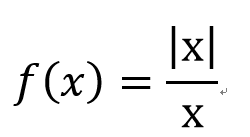
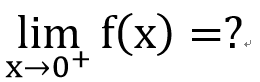
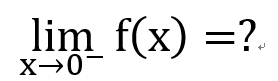
右極限
左極限

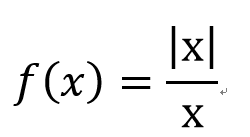
右極限
左極限
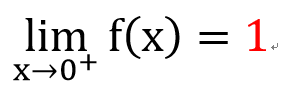
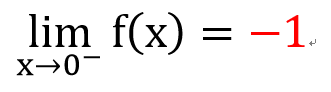
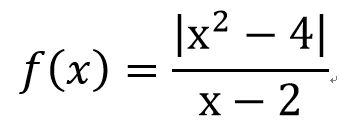
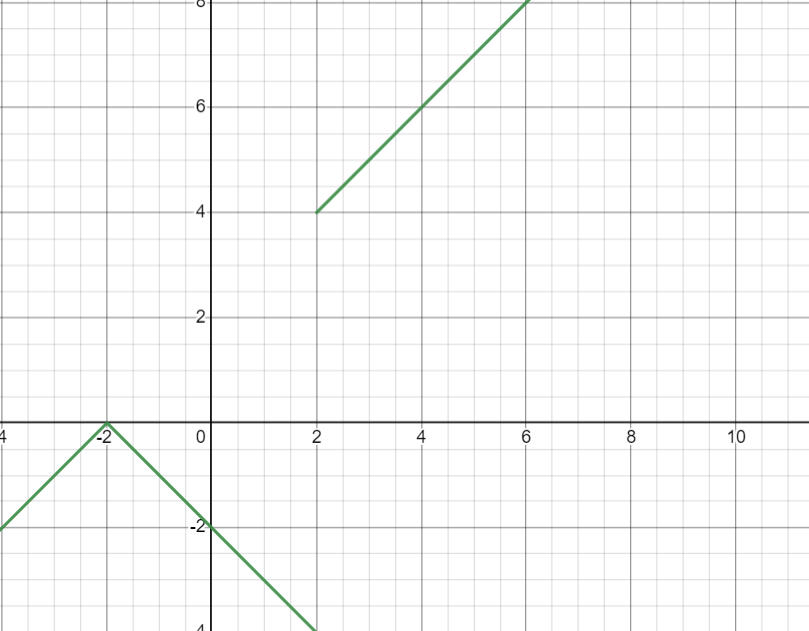
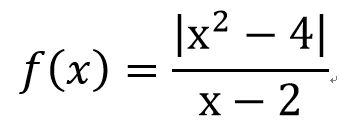

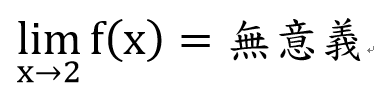
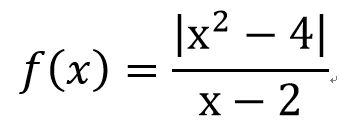

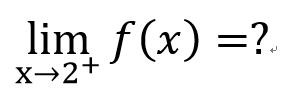
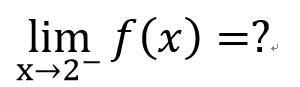
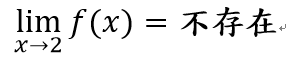

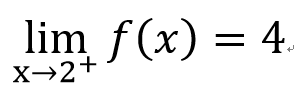
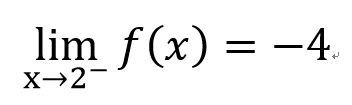
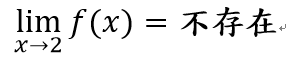
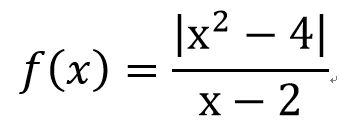
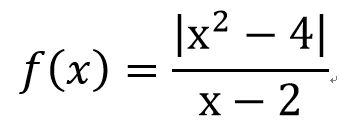

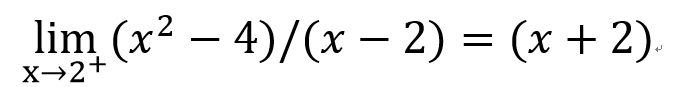
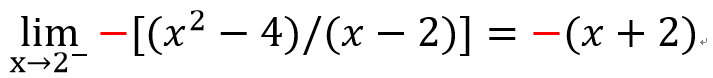
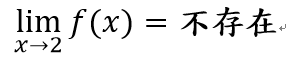
那前面的例子
有左右極限嗎??
那前面的例子
有左右極限嗎??
有!!
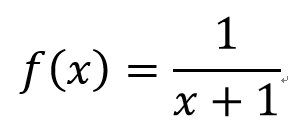

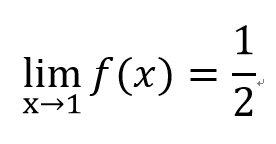
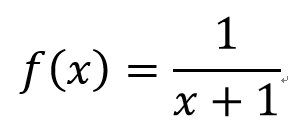

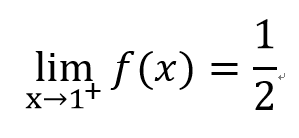
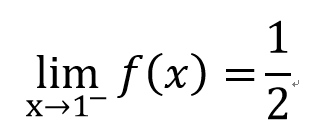
發現?
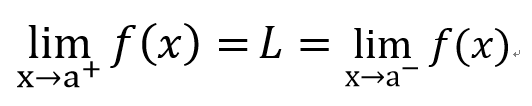
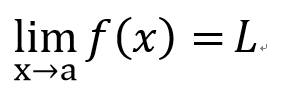
⇔

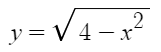
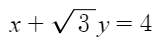
圓:
直線:
P
Q
透過極限找直線斜率!

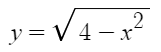
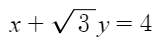
圓:
直線:
P
Q
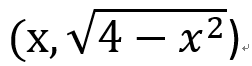
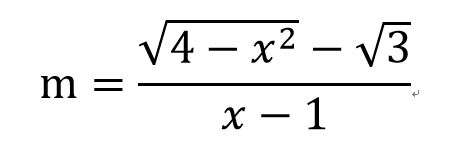
=m(x)

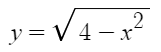
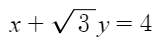
圓:
直線:
P
Q
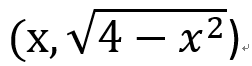
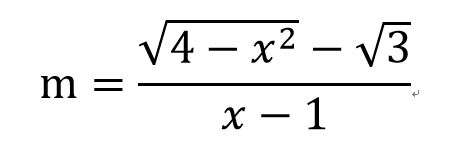
=m(x)
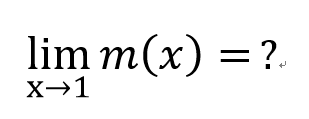

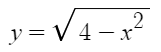
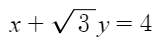
圓:
直線:
P
Q
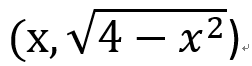
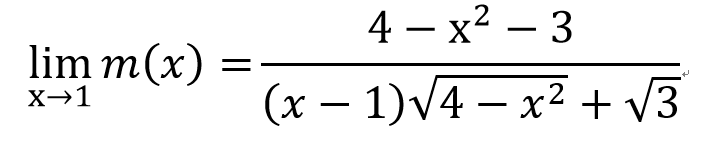

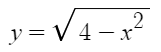
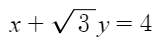
圓:
直線:
P
Q
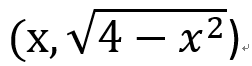
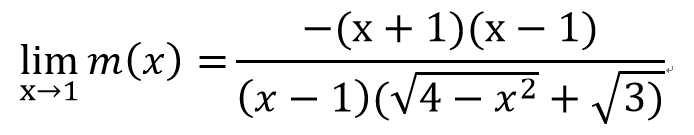

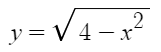
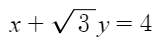
圓:
直線:
P
Q
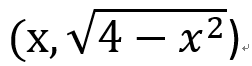
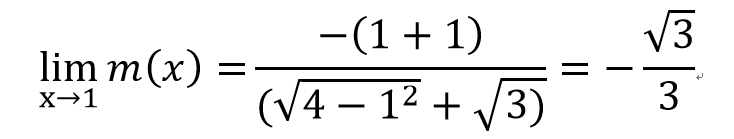

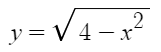
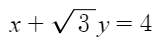
圓:
直線:
P
Q
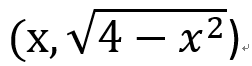
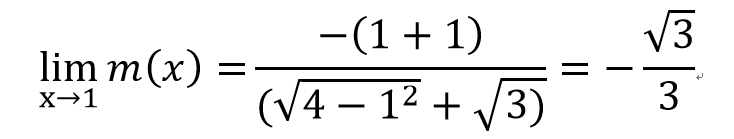
- f(a)有定義
- f(x)在a的極限值存在
- f(x)在a的極限=f(a)
連續函數
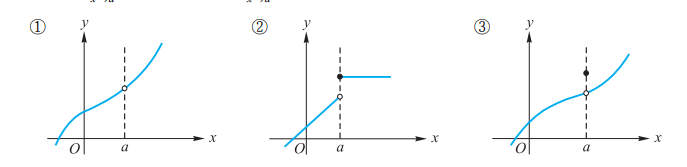
極限題目練習!

- 1
- 2
- 3
- 4
- 5
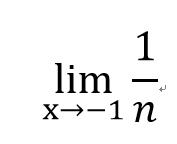
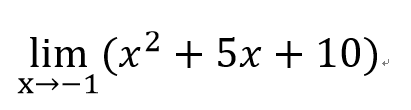
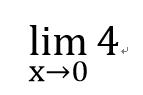
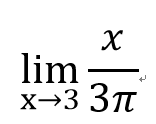
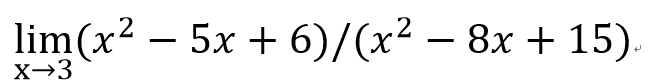
- 1
- 2
- 3
- 4
- 5
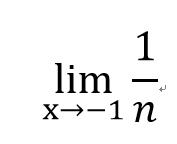
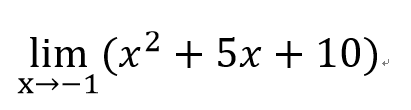
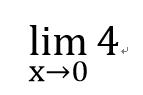
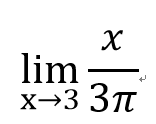
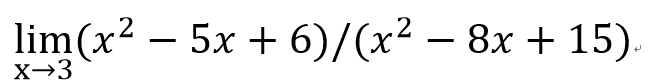
=-1
=16
=4
=1/𝝅
=-1/2
- 1
- 2
- 3
- 4
- 5
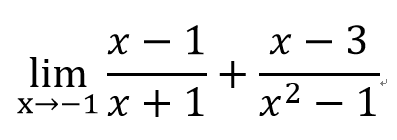
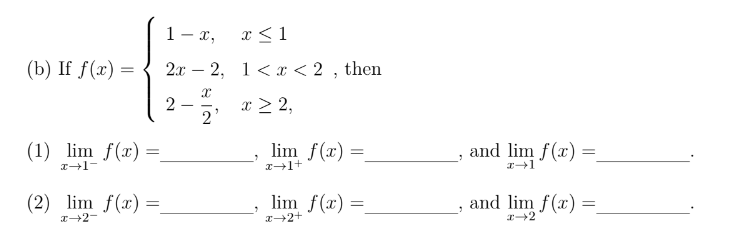
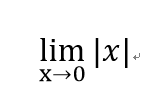
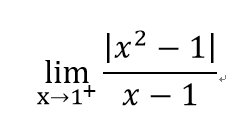
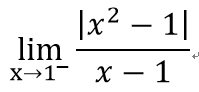
- 1
- 2
- 3
- 4
- 5
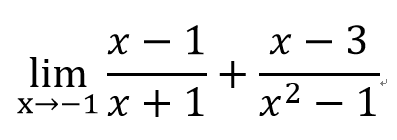
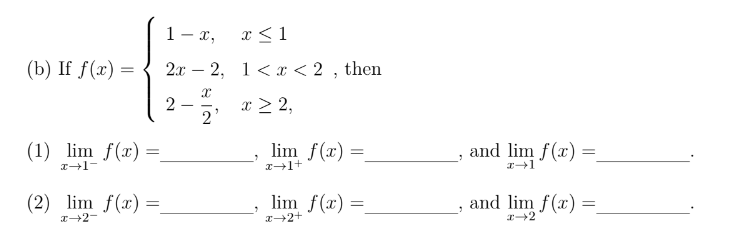
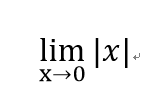
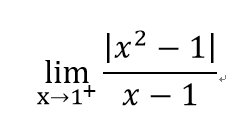
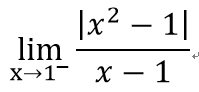
=3/2
=2
=-2
不存在
0
0
0
0
1
2
不存在
導數和導函數

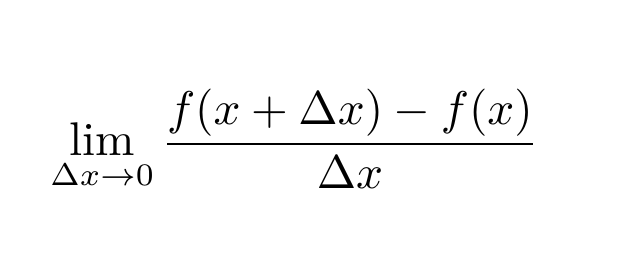

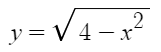
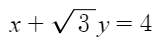
圓:
直線:
P
Q
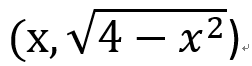
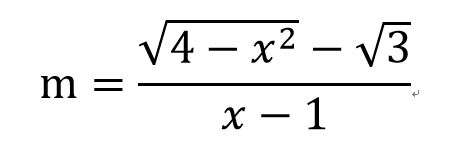
=m(x)
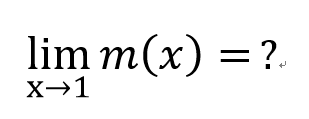

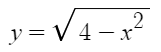
圓:
P
Q
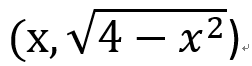

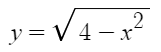
圓:
P
Q
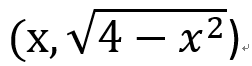
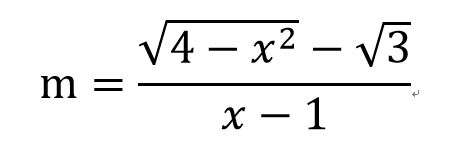

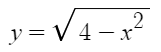
圓:
P
Q
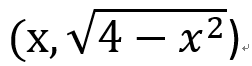
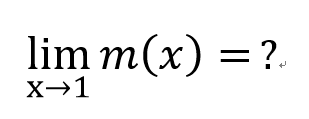

圓:
P
Q
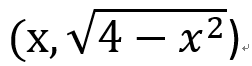
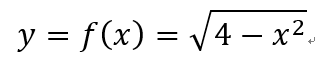

圓:
P
Q
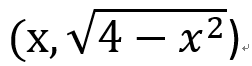
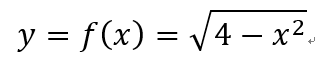
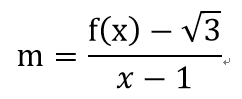
Definition
- 給定函數f(x),若 存在,稱f(x)在這處可微分,且稱此處的極限為在x=a處的導數,以符號f'(a)表示,即
並且稱f'(a)為f(a)的導函數
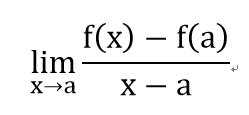
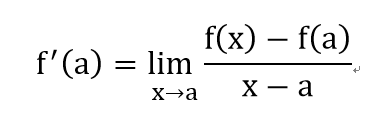

圓:
P
Q
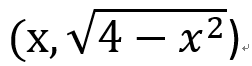
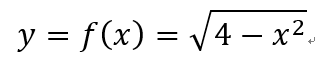
給定的函數f(x)

圓:
P
Q
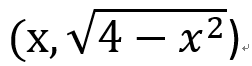
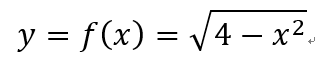
給定的函數f(x)
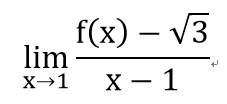
該極限存在

圓:
P
Q
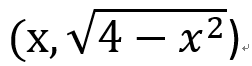
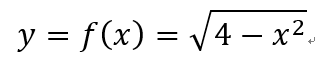
給定的函數f(x)
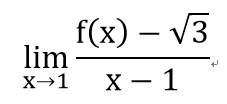
該極限存在
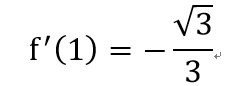
是非題:
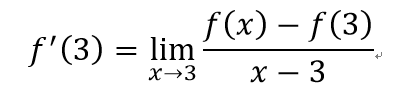
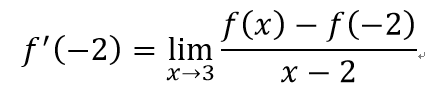
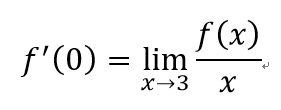
是非題:
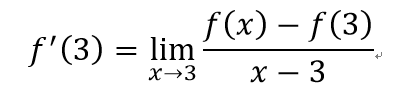
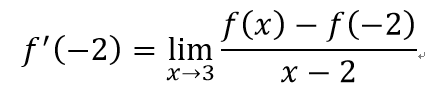
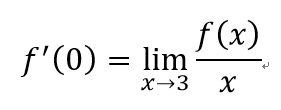
X
O
X
是非題:
若函數f(x)的圖形在x=0處的切線斜率為水平線,則f'(0)不存在。
若函數f(x)的圖形在x=3處的切線為y=2x+5,則f'(3)=2。
是非題:
若函數f(x)的圖形在x=0處的切線斜率為水平線,則f'(0)不存在。
若函數f(x)的圖形在x=3處的切線為y=2x+5,則f'(3)=2。
X
X
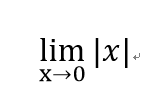
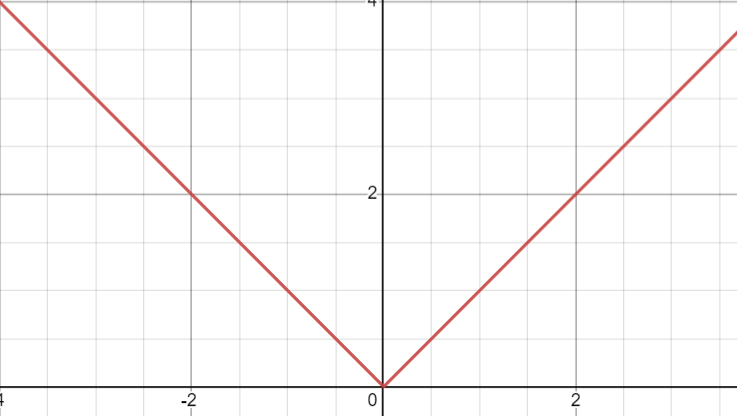
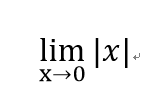

討論左右極限:
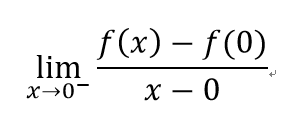
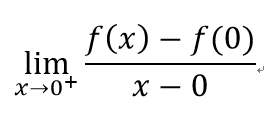
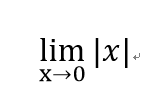

討論左右極限:
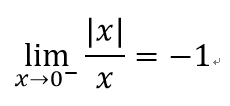
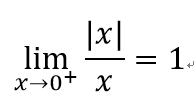
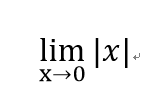

討論左右極限:
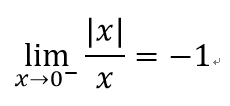
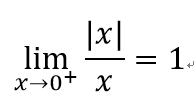
左導數不等於右導數,不可微
導函數
- f'(x)也會寫成 或者若f(x)=2x+1,則f'(x)也可寫成(2x+1)'
- 針對導函數f'(x)若再求它的導函數, 以符號f''(x)表示,稱為f的二階導函數
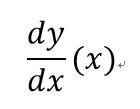
物理應用:
位置、速度和加速度
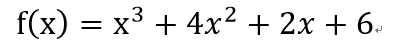
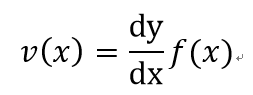
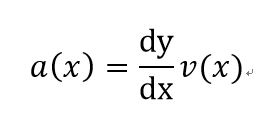
物理應用:
位置、速度和加速度
斜率:平均速率
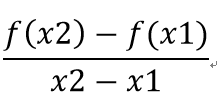
極限:瞬時速率
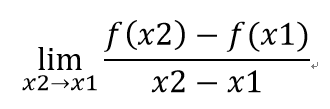
結論:
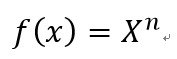
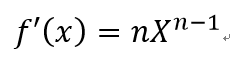
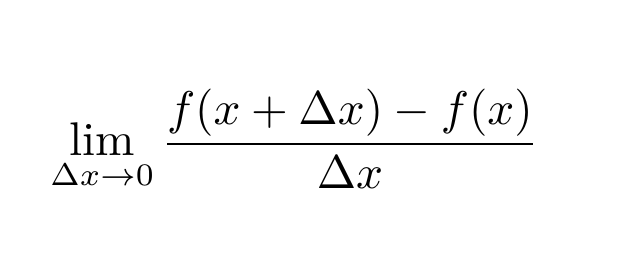
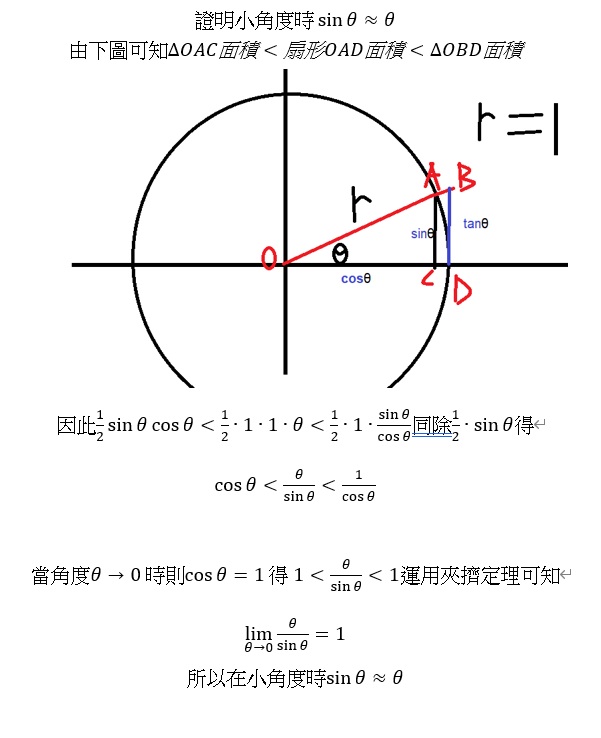
證明:
補充:
c
b
a
θ
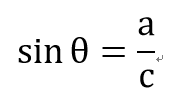
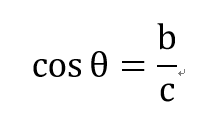
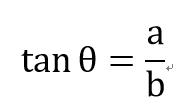
補充:
5
3
4
θ
補充:
5
3
4
θ
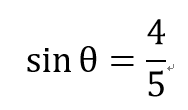
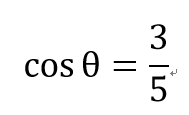
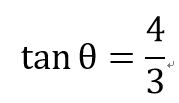
補充:
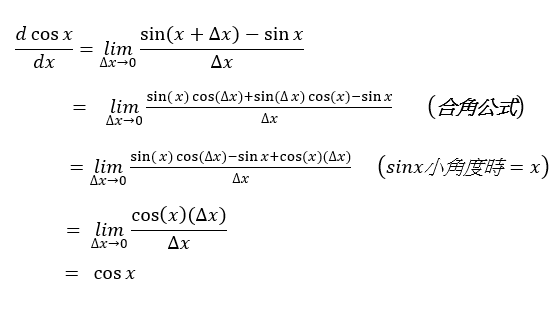
sin
補充:
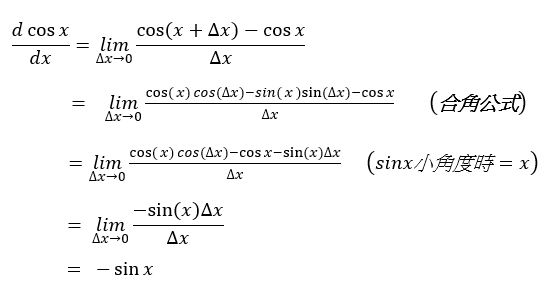
補充:
(不定)積分和定積分



- 由導數f'(x)求出f(x)的表達式(求反導數)
- C為任意常數
不定積分
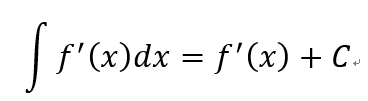
**此時f(x)的表達式並不唯一**
不定積分
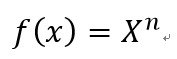
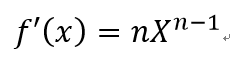
不定積分
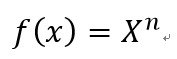
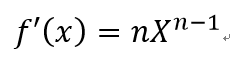
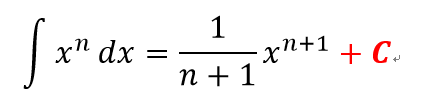
不定積分
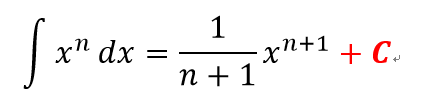
- 1
- 2
- 3
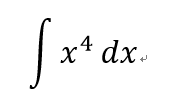
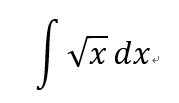
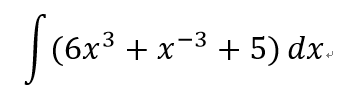
不定積分
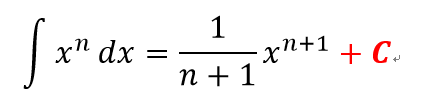
- 1
- 2
- 3
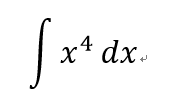
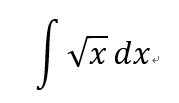
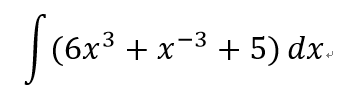
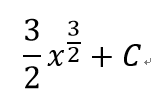
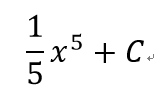
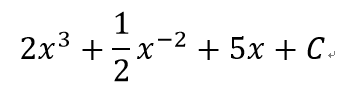
- 求出黎曼和
定積分
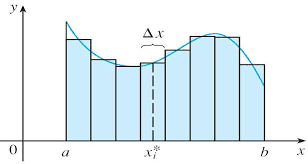
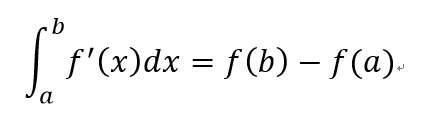
微積分基本定理
若函數f(x)在[a,b]區間上為連續函數,且F(x)是f(x)的一個反導函數(就是f(x)=F'(x)的意思啦),任一反導函數皆可,則有
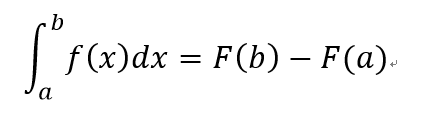
翻譯:
是函數在區間[a,b]上的定積分。
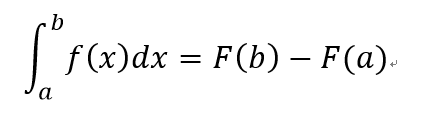
練習:
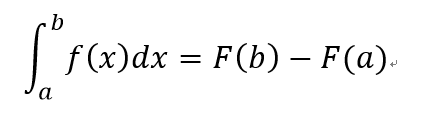
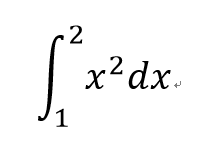
- 1
- 2
- 3
- 4
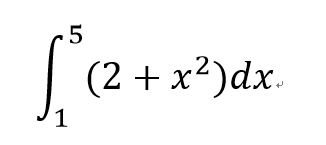
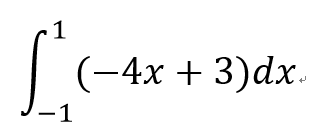
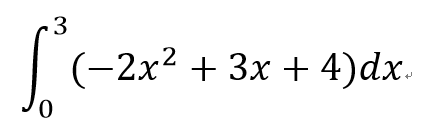
練習:
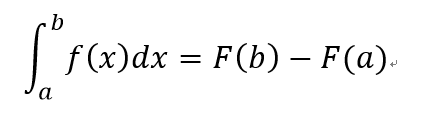
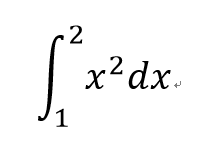
- 1
- 2
- 3
- 4
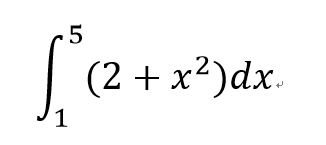
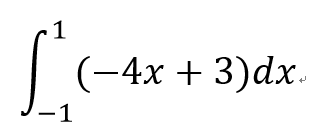
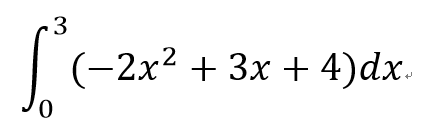
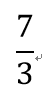
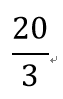
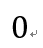
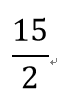
Sources:
calculus
By Wu Phoebe
calculus
- 181