End-to-End Translation Validation for the Halide Language
OOPSLA'22
Basile Clément Inria & ENS, France
Albert Cohen Google, France
At the highest level
- Task: translation validation from a tensor language to an imperative array-based language
- Scope restriction: only affine program are considered
- Approach: symbolic execution based on an affine solver and a general SMT solver
- Key idea: "prophetic" annotation (predicts the value to write in terms of tensors) generated by compiler to handle loops
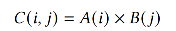

Is the one below a refinement (instantiation) of the one above?
Overview with examples
- What is Halide language?
- What are the proof obligations in our translation validation task?
- What is prophetic and how does it help us to handle loops?
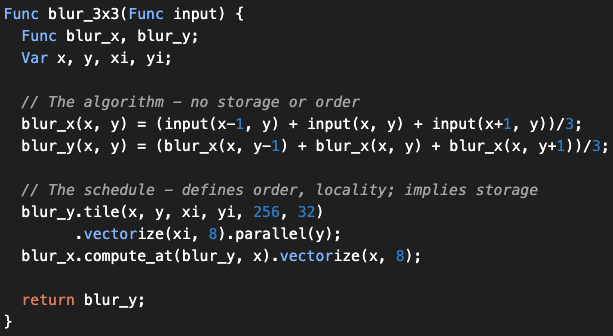
Halide language
- DSL for high-performance image and array processing
- A base for TVM-like ML compiler
- A library of optimizations are utilized as "schedule"s
- (SIGGRAPH'12,16,18,19),(PLDI'13),(CACM)
Ex1: Outer product
Proof obligations:
- (coverage of writes) All locations of 0 <= i < N, 0 <= j < M are written.
- (definedness of reads) All array accesses are in bounds.
- (equality of values) Results in arrays are as expected in tensors.
1 and 2 are checked by an affine solver, and 3 is checked by a general SMT solver.
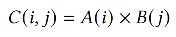

Ex2: Matrix Multiplication
Challenge for obligation 3: recurrence of loop (a iteration may depend on previous iterations)
Key insight: scheduling compiler could generate prophetic expressions.
The prophetic expression lives in the specification world, and predicts the value that will be written by the assignment in terms of tensors.
This reduces our problem to the translation validation between specifications and prophetic version implementations, both playing with tensors.
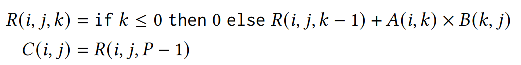

Recap of the overview
- The expressions used in array indices, loop bounds and conditionals must be (quasi-)affine. This ensures to track the values read and written from arrays.
- The assignments are annotated with prophetic expressions consisting of tensors.
Technique details
- Affine program: Halide specification as Systems of Affine Recurrence Equations
- Sched language as target language with annotations
- Semantics: from dynamic one to symbolic one
Systems of Affine Recurrence Equations
SARE is a set of equations
- x_1, ..., x_{n_A} are regarded as indices
- A is regarded as a tensor
- phi is regarded as a filter
- "recurrence" means A could appear in the right hand side
For recurrence indices, the dimension of tensors are extended as follows.
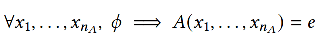
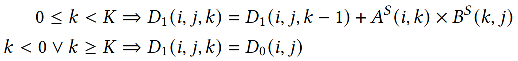
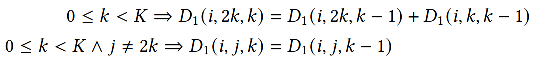
Ex: matrix multiplication
Ex: D(i, 2k) += D(i, k)
Sched language
An annotated imparative language as target language.

- quasi-affine expression
- local array allocation
- sequential and parallel loop
Sched language: well-formedness

Update semantics

Why update semantics?
1. It's easy to symbolize accumulated updates for sequential loops.
2. A lightweight way to capture semantics of parallel loops. (No data race)
Two entries are collected:
- updates of memory
- reads of memory
Symbolic semantics

C is a symbolic set of equalities, with affine quantification. It will collect prophetic equality from assignments as VCs.
(S-SeqLoop) requires a inductive checking for each possible iteration.
(S-Assign) checks accesses are in-bound and rhs expression is defined, and, collects VCs and reads.
A symbolic heap is a finite union of symbolic chunks.
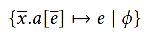
Experiments
- Implementation
- Evaluation
- Limitations
Implementation
- written in Ocaml
- isl library for affine solver and expression
- Z3 as a SMT solver
- instrument Halide compiler to generate prophetics
- Many simplications and approximations in details
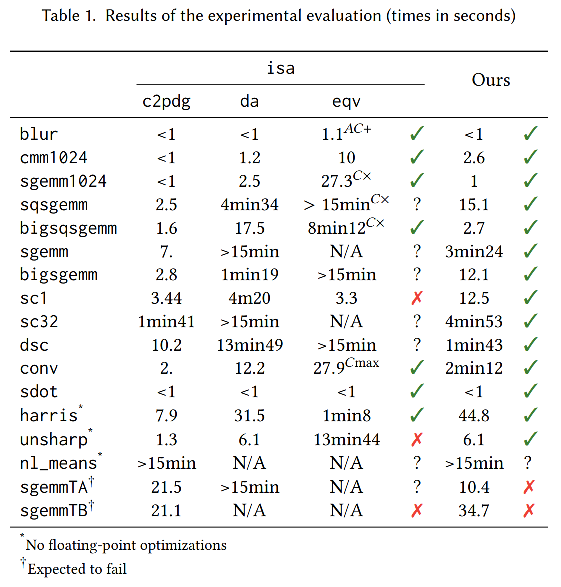
Evaluation
Benchmarks from Halide repository:
- some are not affine, e.g., data-dependent accesses
- some have unsupported features
Compared to unannotated one.
Results:
- Faster on 13/14 cases.
- Both unexpectedly fail on 1 cases. (nl_means)
- Fail as expected on 2 cases.
Limitations
Considering mathematical integer and real as base type omits:
- Overflow checking
- IEEE754 format floating-point numbers does not obey associativity and has special number inf and NaN
Assume affine specification results in affine implementation, which is generally not true. For example, to calculate C = aA + bB, an optimized implementation usually checks if a = 0 and ignores aA.
It will be more believable to produce mechanized formal correctness proofs in a proof assistant like Coq.
TV-for-Halide
By Xingyu Xie
TV-for-Halide
- 107



