Probability
yennnn
什麼是機率?
實數 p \in [0, 1] \\
描述事件發生的可能性高低
\( p = 1 \):事件絕對發生
\( p = 0 \):事件絕不發生
怎麼算?
組合
p = \frac{所有可能發生的事件數}{滿足條件的事件數}
乘法原理
拆解事件發生的步驟,把每個步驟的機率乘起來
事件
樣本空間:所有可能發生結果的集合
事件:樣本空間的子集
必然事件:樣本空間的全集
不可能事件:空集合
基本事件:只包含一個樣本空間元素
餘事件( \( \bar{A} \) )
\(A\)不發生的事件
- \( P( \bar{A} ) = 1 - P(A) \)
聯集( \( A \cup B \) )
\(A 或 B 發生的事件\)
- \( P( A \cup B ) = P(A) + P(B) - P(A \cap B) \)
- \(特別當 A 和 B 互斥時,則有\)
- \( P( A \cup B ) = P(A) + P(B) \)
條件機率
\( P(A\mid B):已知B發生下,A發生的機率\)
- \( P(A \mid B) = \frac{P(A \cap B)}{P(B)} \)
獨立事件
A 的發生與否不影響 B 是否發生\\
\\
B 的發生與否亦不影響 A 是否發生
P(A \mid B) = P(A)\\
P(B \mid A) = P(B)
代回去剛剛條件機率的定義:
\( P(A \mid B) = \frac{P(A \cap B)}{P(B)} \)
P(A \cap B) = P(A) \times P(B)
期望值
有點像平均值的概念
就是以機率為權重的加權平均
E[X] = \sum_x P(X = x)x
期望值小性質
他可以加!
E[X_1 + X_2 + ... + X_n]
\\= E[X_1] + E[X_2] + ... + E[X_n]
機率分布
均勻分布
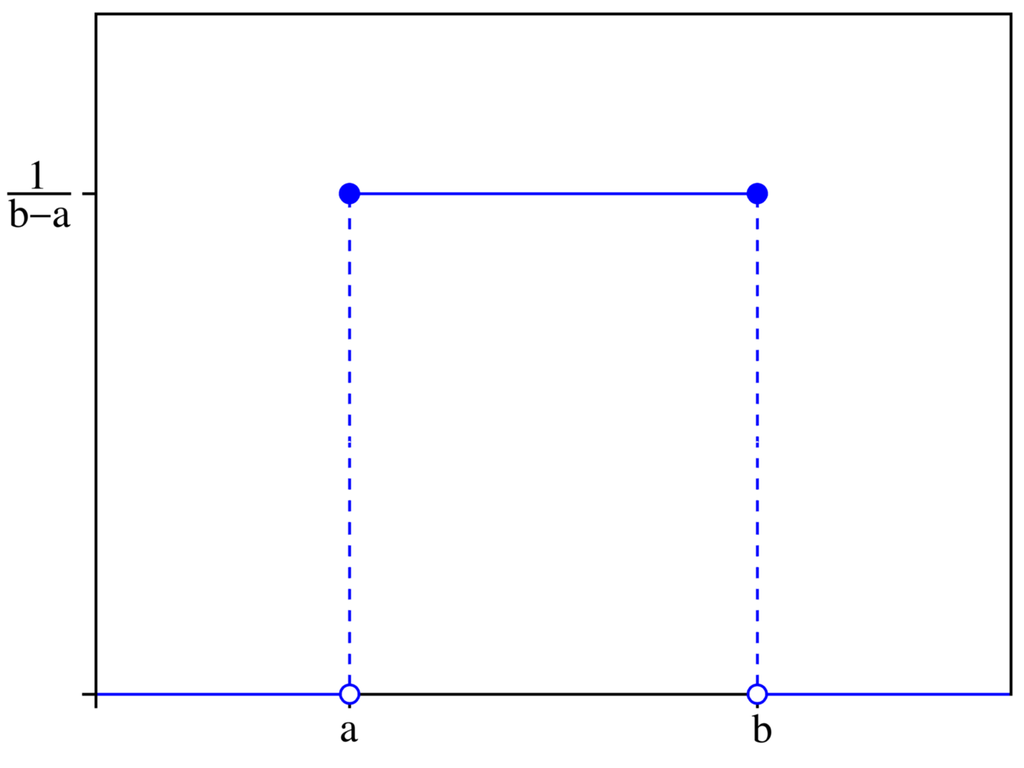
- \(若有n個可能事件,每個事件發生機率都是 \frac{1}{n} \)
- eg : 丟骰子
E[X] = \frac{a + b}{2}\\
a : 最大值, b : 最小值
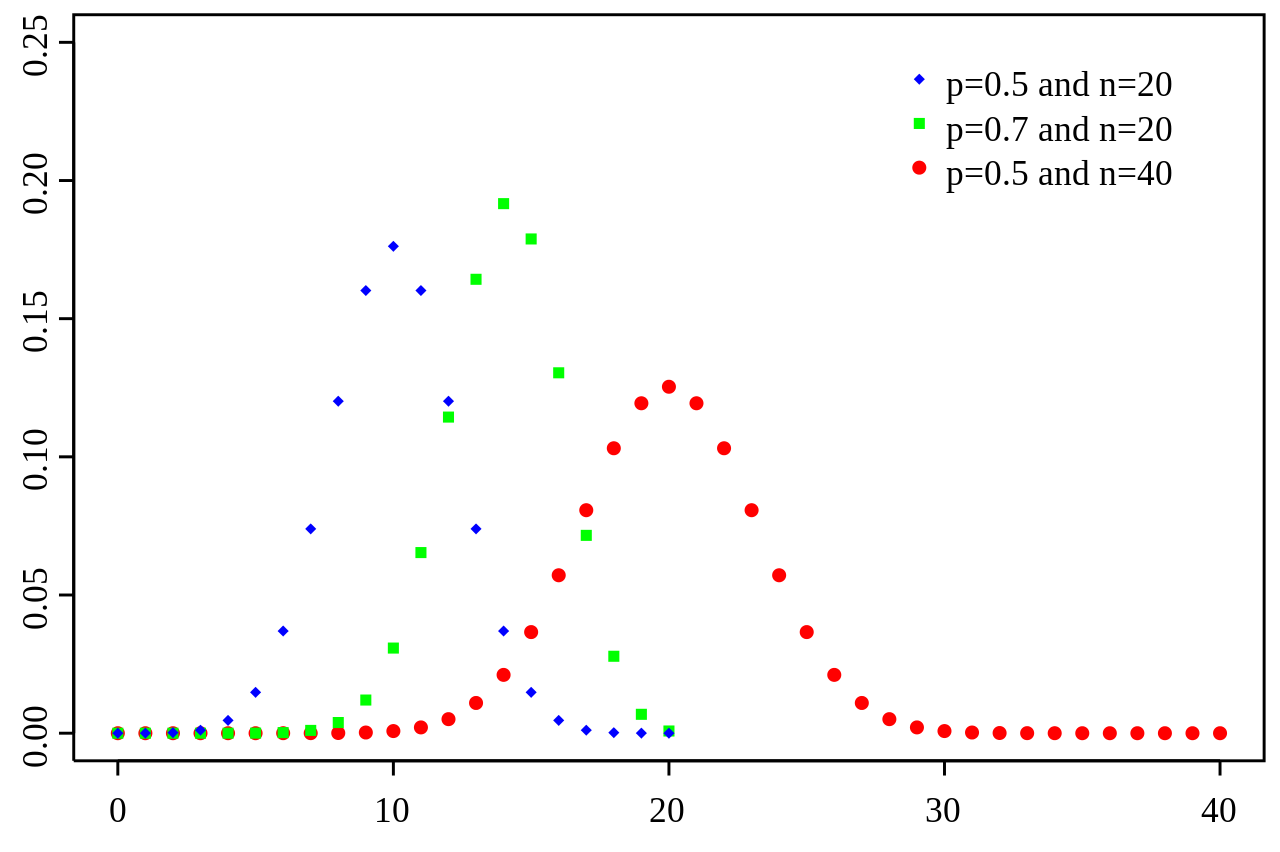
二項分布
- \(做n次是/非試驗,每次成功機率p,\\成功次數的機率分布即為二項分布\)
- eg : 投10次硬幣出現正面的機率分布
P(X = x) = \binom{n}{x} p^x (1 - p)^x
E[X] = pn
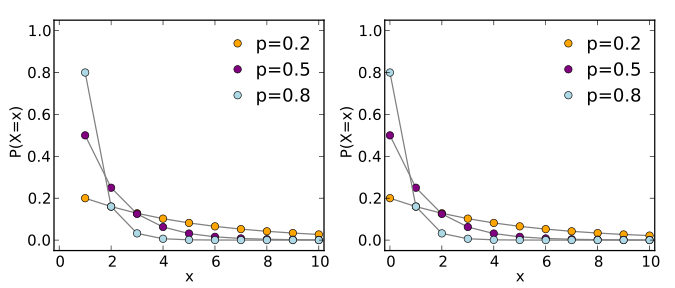
幾何分布
- \(做多少次是/非試驗才得到第一次成功的機率分布\)
- eg : 投硬幣
- \(若每次成功的機率p,在第k次成功的機率\)
P(X = k) = (1 -p)^{k - 1} p
E[X] = \frac{1}{p}
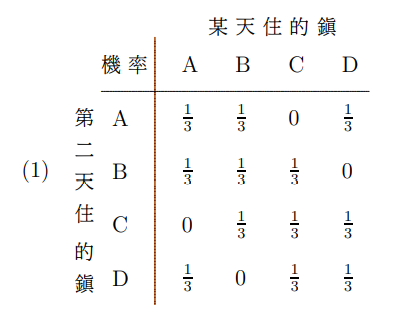
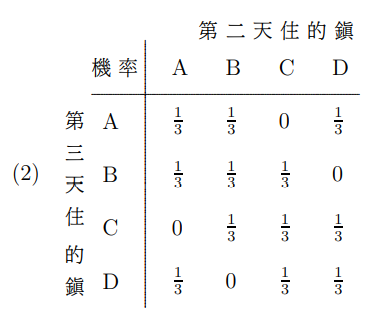
馬可夫鏈
由現在的狀態
透過推移矩陣
推到下一個狀態
舉個例題ㄅ


隨機演算法
Monte Carlo Algorithm
蒙地卡羅演算法
- 大量亂數模擬真實狀況
- 漸漸接近最優解
- 不保證解的正確性
Las Vegas Algorithm
拉斯維加斯演算法
- 隨機亂數枚舉
- 均攤矇到最優解的機率
- 保證解的正確性
找第k大
給定一亂序序列,找序列第k大
排序後取第k項:\(O(n \log n)\)
- \(隨機選序列中的一個數x\)
- \(把比x小的數放到x左邊,比較大的放到右邊 \Rightarrow O(n)\)
- \(此時x左邊有a個數,右邊有b個數:\\若a == k ,x即為所求;\\若a < k ,在x的右邊隨機選一個數再做一次;\\若a > k,在x的左邊隨機選一個數再做一次\)
Las Vegas
因為是隨機選,所以每次大概都把序列切成 \frac{1}{2}\\
n + \frac{n}{2} + \frac{n}{4} + ... < 2n\\
均攤複雜度O(n)\\
最佳情況O(1)\\
最差情況O(n^2)\\
矩陣相等
\(給定A, B, C三個n \times n 方陣,判斷AB是否等於C\)
\(直接做出AB \Rightarrow O(n^3)\)
注意到:
- \(一個n \times n 矩陣乘以 n \times 1矩陣只需要O(n^2)\)
- \(乘出來變成 n \times 1矩陣\)
- \(矩陣滿足結合律,即(A \times B) \times X = A \times (B \times X)\)
- \(若A \times B = C,則A \times B \times X = C \times X\)
我們可以 Claim :
\(若A \times B \times X = C \times X\)
\(則 A \times B = C \)
顯然不是絕對會對,但我們可以看看他錯的機率有多高
嗎?
\(若A \times B \neq C \\ 則A \times B \times X = C \times X \\之機率有多高?\)
考慮D = A \times B - C\\
\because A \times B \neq C\\
\therefore \exist d_{ij} \in D \neq 0\\
\\
假設G = D \times X\\
則 g_{i} = \sum_{k=1}^{n} d_{ik} x_k\\
= d_{i1}r_1 + ... + d_{ij}r_j + ... + d_{in}r_n\\
= d_{ij}r_j + y\\
P[g_i = 0] = \\P[g_i = 0 | y = 0] \cdot P[y = 0] + P[g_i = 0 | y \neq 0] \cdot P[y \neq 0]\\
P[g_i = 0 | y = 0] = P[x_i = 0] = \frac{1}{2}\\
P[g_i = 0 | y \neq 0] = P[x_j = 1 且 d_{ij} = -y] \\ \leq P[x_j = 1] = \frac{1}{2}\\
P[g_i = 0] \leq \frac{1}{2} P[y = 0] + \frac{1}{2} P[y \neq 0]\\
= \frac{1}{2} P[y = 0] + \frac{1}{2}(1 - P[y = 0])\\
= \frac{1}{2}
P[G = 0] \\
= P[g_1 = 0 \wedge ... \wedge g_i = 0 \wedge ... \wedge g_n = 0]
\leq P[g_i = 0]\\
\leq \frac{1}{2}
如果我們多做幾次幾乎不可能發生
Monte Carlo
- \(隨機生成n \times 1 矩陣X\)
- \(先做AX,變成n \times 1 矩陣M \Rightarrow O(n^2)\)
- \(做BM,變成n \times 1矩陣N \Rightarrow O(n^2)\)
- \(做CX,變成n \times 1矩陣P \Rightarrow O(n^2)\)
- \(如果N == P,就說AB == C\\否則說AB \neq C\)
塗色問題
\(給一個V點E邊的圖\\找出一種只用兩種顏色的塗色方法\\使得至少 \frac{E}{2} 條邊的兩端點是不同顏色\)
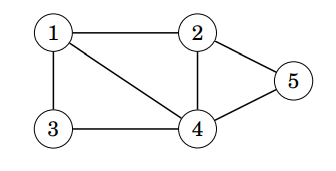
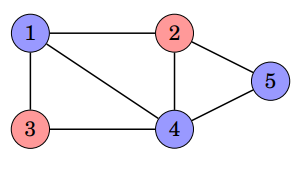
Las Vegas
直接隨機幫每個點選一種顏色
然後檢查是否滿足條件
不滿足就再選一次
因為每個邊端點顏色不同的機率是\(\frac{1}{2}\)
所以期望值是\(\frac{m}{2}\)
理論上不會做太多次就可以找到
Probability
By yennnn
Probability
- 480


