cog sci 131 section
week 04/18/22
by yuan meng
agenda
- weber's w (piantadosi, 2016)
- implement metropolis-hastings
- hw9 prompt walkthrough
weber ratio W
measures the acuity of the approximate number system (ans)
- a large number n is represented as a normal distribution centered at n
- the probability that we say n1 ≥ n2 when it's indeed the case is a function of n1, n2, and W
two packs of extremely dangerous dogs 👉 which pack has more?
\mathcal{N}(n,\, W\cdot n)
P(\mathrm{correct}|W, n_1, n_2) = \Phi \left[ \frac{ |n_1 - n_2| } { W \cdot \sqrt{n_1^2 + n_2^2} } \right]
probability of getting it right 👉 this small area
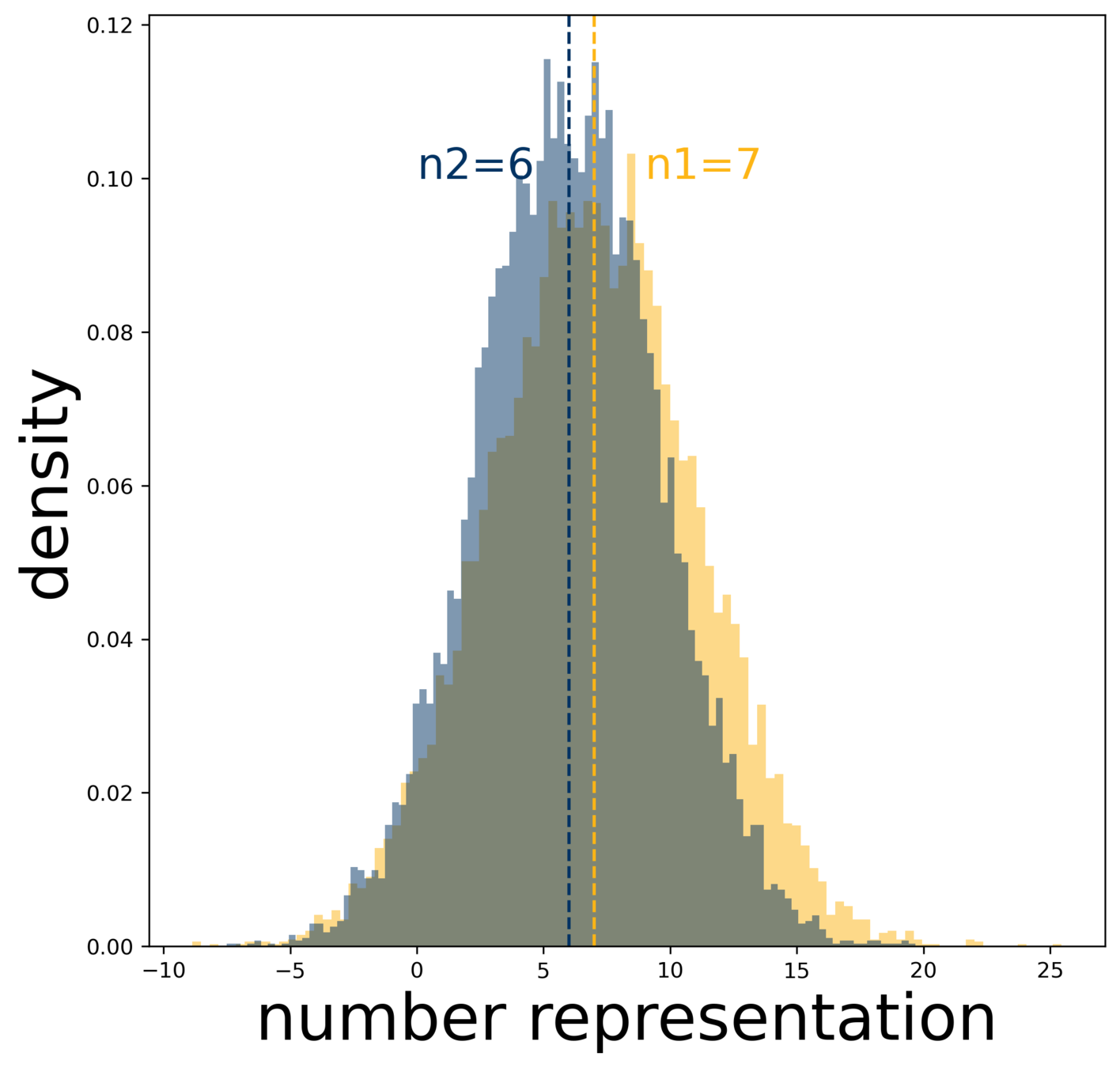
weber ratio W
infer W from response data
- prior of W (prior is 0 if W < 0):
- likelihood given k data points:
- unstandardized posterior of W:
P(W) = e^{-W}
\displaystyle{P(a|W,n_1, n_2) = \prod_{i}^{k} P(a_i|W, n_{1i}, n_{2i})}
\displaystyle{P(W|a, n_1, n_2) = P(W) \cdot \prod_{i}^{k} P(a_i|W, n_{1i}, n_{2i})}
\displaystyle{\log P(W|a, n_1, n_2) = \log P(W) + \sum_{i}^{k} \log P(a_i|W, n_{1i}, n_{2i})}
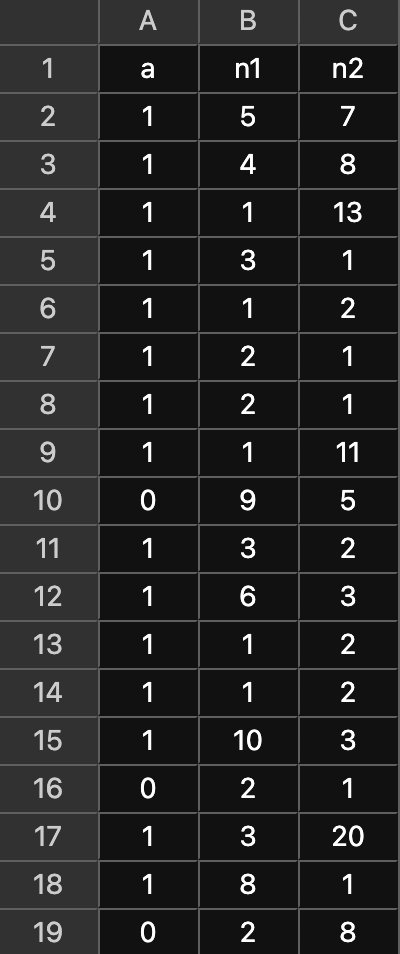
data: each trial is a judgment (is n1 ≥ n2?); a = 1 indicates answer is correct
be sure to take log!
implement metropolis-hastings
- goal: collect representative samples from the posterior distribution of W
-
the sampling algorithm
- initialize: pick a random W
- propose: W' = W + noise
-
decide whether to accept W'
- if P(W'|D) > P(W|D), definitely accept
- even if P(W'|D) ≤ P(W|D), accept W' with a P(W'|D)/P(W|D) probability
- iterate over 1-3, each time starting with the last accepted W
- sampling vs. optimization: a sampler doesn't alter the value of W, but an optimizer (e.g., gradient descent) does
- burn-in: sometimes, we can discard the first bunch of samples which may not be good
most challenging bit
- need to adapt original criteria to log-transformation
- if cleverly written, can use one simple if-statement to catch both acceptance conditions
hw9 prompts
samples from posterior
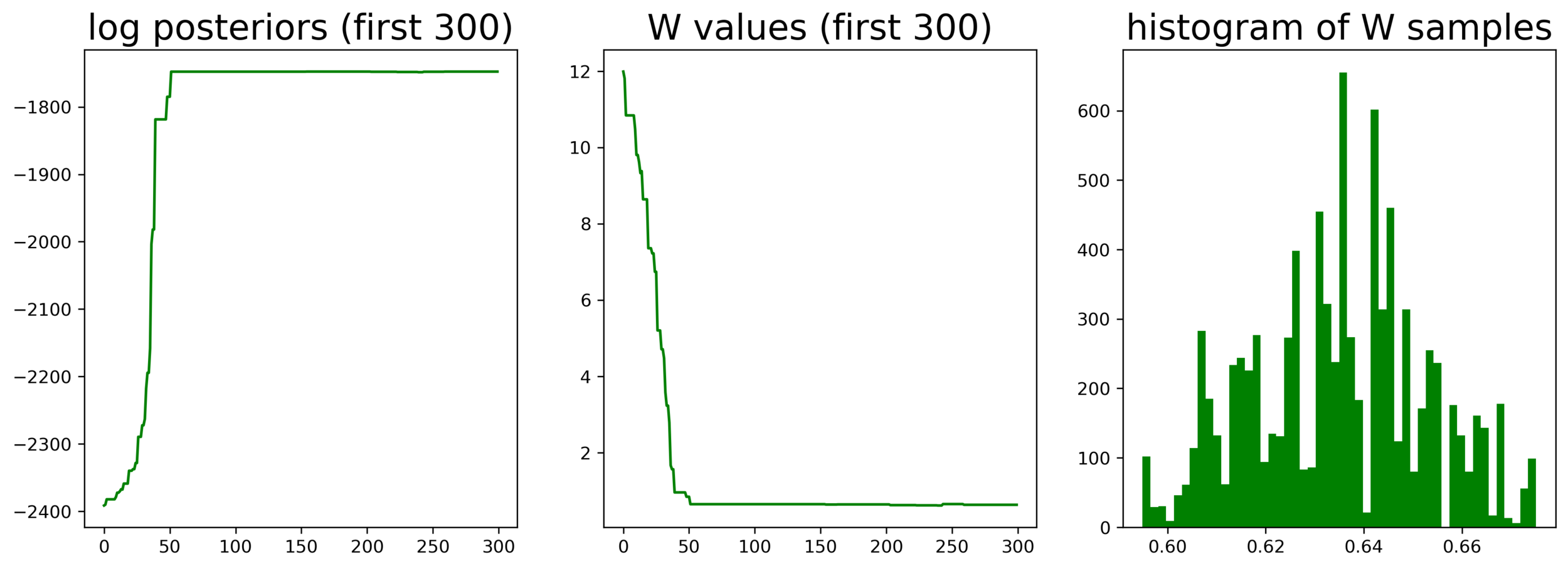
homework 9, q5
samples from prior
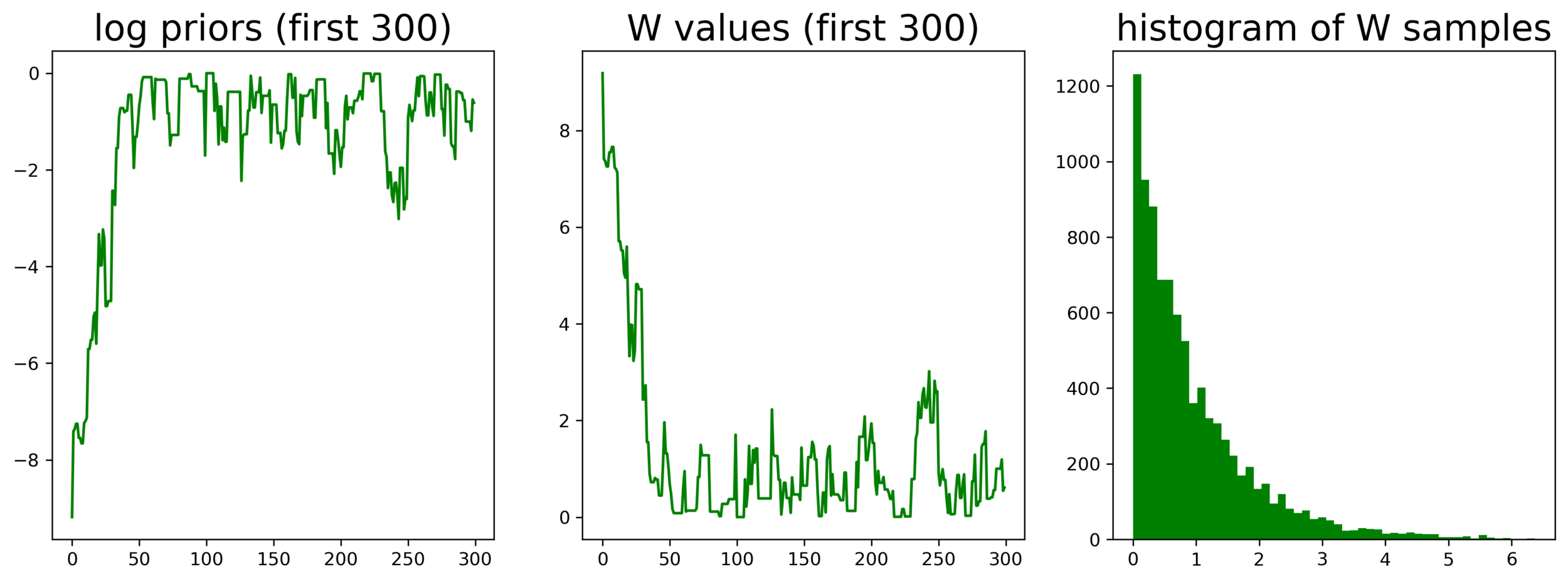
homework 9, q7
bayesian cognitive model
vs. bayesian data analysis
bayes as a model of cognition: a normative model that dictates what an ideal learner should do given data and prior
bayes as a data analysis tool: a descriptive model that captures what a real learner did do given data and prior
the same prior and data lead to the same inference 👉 if prior is optimal, then inference is optimal
e.g., seeing 100 heads in a row, the probability that the tosser is a psychic?
different people may discount observations differently 👉 can learn each person's "discount rate" from data
cogsci131_04_18
By Yuan Meng
