Sergio Rubio-Pizzorno🇲🇽🇨🇱
Más allá de la
prueba de arrastre:
prácticas geométricas de construir y deconstruir con GeoGebra
Conferencia
Sergio Rubio-Pizzorno
@SergioRubioPizzorno 🇲🇽🇨🇱
Más allá de la prueba de arrastre: prácticas geométricas de construir y deconstruir con GeoGebra
- viernes 1 de diciembre de 2023 -
Conferencia
🔸Estudiante del Doctorado en Ciencias con especialidad en
Matemática Educativa del Cinvestav🇲🇽
🔸Embajador GeoGebra
🔸Director de la Comunidad GeoGebra Latinoamericana
Créditos
Charla "Pensar las Matemáticas de manera dinámica con GeoGebra" por Sergio Rubio-Pizzorno se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Basada en una obra en https://slides.com/zergiorubio/olimpiadas-mat-ipn .
BY
NC
Pensamiento geométrico
Ambientes de Geometría Dinámica
Las aplicaciones de la geometría [AGD] varían amplia y crecientemente, dado los desarrollos de visualización y modelación basados en computadores. La aparición de imágenes digitales y dinámicas no solo ha revivido a la disciplina de las matemáticas, también ha cambiado radicalmente la manera en que está siendo enseñada y aprendida en la escuela en estos días.
(Sinclair et al., 2017, p. 457).
- Producir conjeturas, descubrir contraejemplos y aportar ideas sobre cómo demostrar conjeturas (Komatsu y Jones, 2020).
- Comenzar a distinguir entre un objeto
matemático ideal y su representación material (Leung et al., 2023). - Profundizar en el dinamismo, al tener los mismos objetos pero con dos comportamientos dinámicos diferentes (Talmon y Yerushalmy, 2004).
- Inducir invariantes para generar conjeturas por abducción (Baccaglini-Frank y Mariotti, 2010).
- Reconocer que al arrastrar las representaciones dinámicas, estas mantienen las propiedades de acuerdo a las cuales fueron construidas y las propiedades euclidianas (Leung, 2015).
Resultados de
investigación
con AGD
- Verificar y explorar propiedades geométricas (Hölzl, 2001).
- Generar datos, identificar propiedades, evolucionar estrategias de resolución de tareas y generar nuevas preguntas (Laborde, 2005).
- Explorar y explicar tareas geométricas (Fahlgren y Brunström,
2014). - Reconocer propiedades geométricas como invariantes en variación (Leung, 2008).
- Verificar dinámicamente si una construcción está bien hecha mediante la prueba del arrastre (Arzarello et al., 2002).
¿Arrastre?
Transformación continua en tiempo real.
(Goldenberg y Cuoco, 1998, p. 351)
La literatura enfatiza en el arrastre como la característica definitoria de un AGD.
(Fahlgren y Brunström, 2014, p. 298)
Prueba del arrastre
La prueba de arrastre se utiliza como medio para validar una conjetura, en particular las conjeturas que se originan por la visual o una construcción
(Arzarello et al., 2002, p. 68)
Ahora inténtalo tú
Prueba del arrastre
¿Qué cuadrilátero es?
https://www.geogebra.org/classroom/vpgvzvjp
Sergio Rubio-Pizzorno🇲🇽🇨🇱
Más allá de la
prueba de arrastre:
prácticas geométricas de construir y deconstruir con GeoGebra
Conferencia
¿Y si no pasa la
Prueba de arrastre?
Comportamiento dinámico
- El punto A es libre.
- El punto B es libre.
- El punto C está siempre sobre la recta h.
- El punto D es fijo.
¿Por qué se
comportan así?
- El punto A es libre A es independiente.
- El punto B es libre B es independiente.
- El punto C está siempre sobre la recta h C depende de la recta h.
- El punto D es fijo D depende de las rectas g e i.
\Rightarrow
\Rightarrow
\Rightarrow
\Rightarrow
Relaciones de dependencia
¿Qué determina tales deependencias?
Orden de construcción
Rectángulo
Práctica geométrica de Deconstruir
Comportamiento dinámico
Relaciones de dependencia
Orden de construcción
Relaciones geométricas
Propiedades geométricas
Supongamos que quería un cuadrado:
¿Cómo lo construyo?
Comportamiento dinámico
Relaciones de dependencia
Orden de construcción
Relaciones geométricas
Propiedades geométricas
Propiedades geométricas
No se cumple la propiedad de la congruencia de todos los lados
Relaciones geométricas
Orden de construcción
Relaciones de dependencia
Comportamiento dinámico
Orden de construcción
Propiedades geométricas
Relaciones geométricas
Relaciones de dependencia
Comportamiento dinámico
Práctica geométrica de Construir
Orden de construcción
Propiedades geométricas
Relaciones geométricas
Relaciones de dependencia
Comportamiento dinámico
Deconstruir
Construir
Prácticas geométricas
Rubio-Pizzorno, Montiel-Espinosa y Moreno-Armella, 2021, p. 16
¿Qué más?
¡Gracias TOTALES!
Sergio Rubio-Pizzorno🇲🇽🇨🇱
¡Suscríbete!
Más allá de la prueba de arrastre: prácticas geométricas de construir y deconstruir con GeoGebra
By Sergio Rubio-Pizzorno
Más allá de la prueba de arrastre: prácticas geométricas de construir y deconstruir con GeoGebra
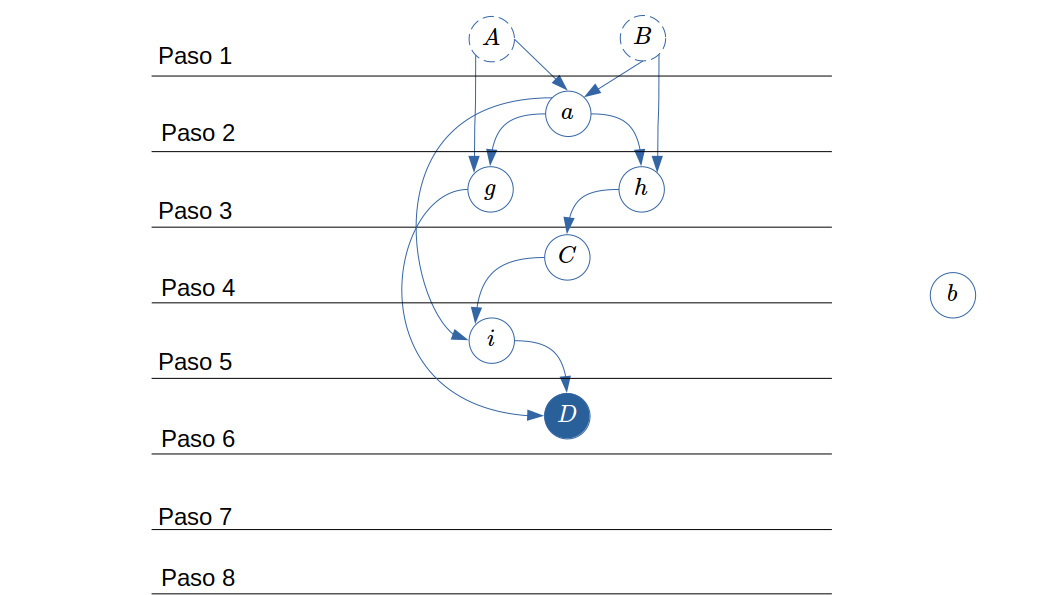
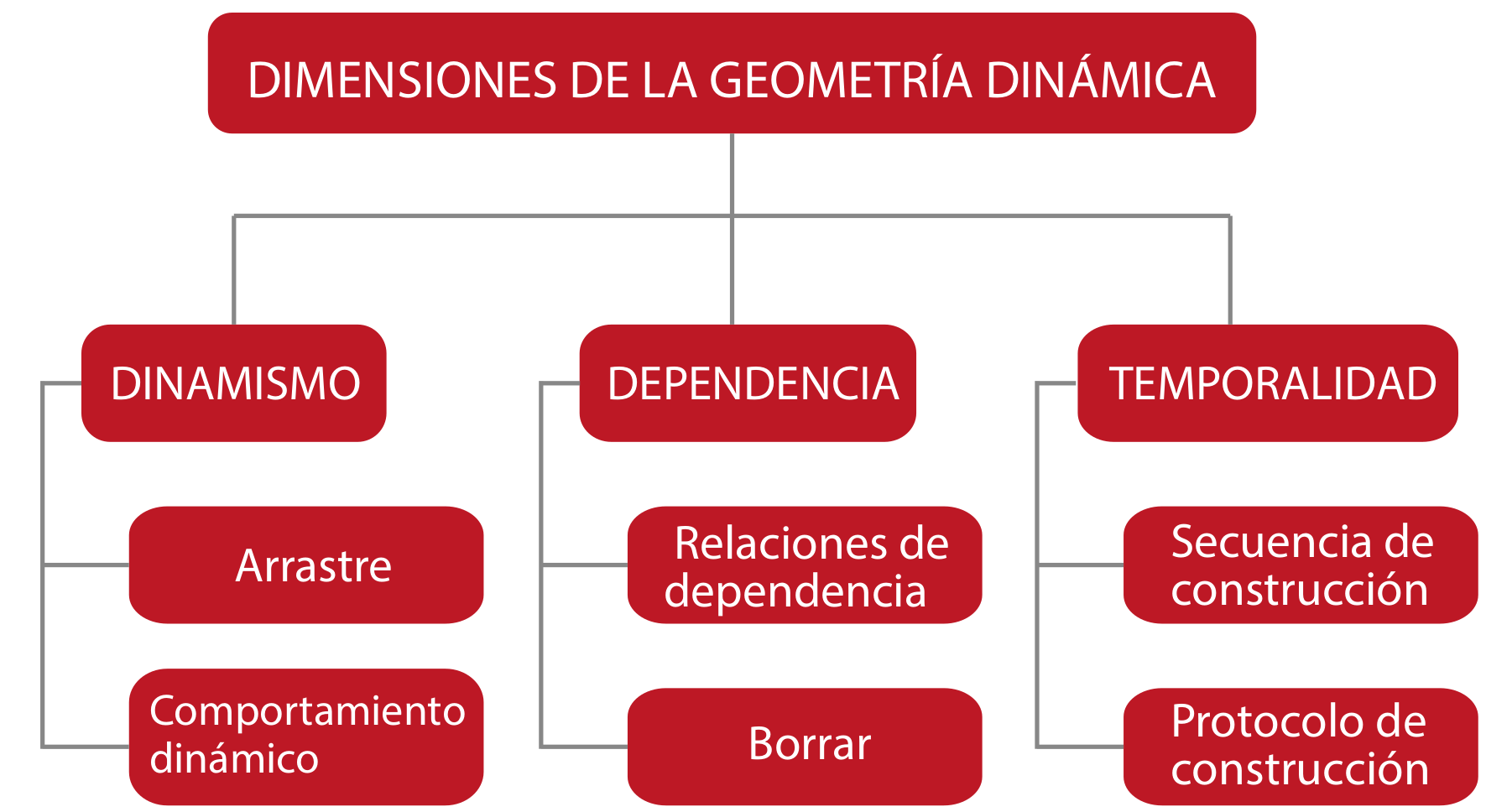
La investigación sobre Geometría dinámica se ha centrado principalmente en el arrastre —su característica definitoria— y sus implicaciones dinámicas, como por ejemplo, verificar si una construcción fue bien construida utilizando la prueba del arrastre. Pero, ¿hay algo más allá en la Geometría dinámica? La respuesta a la pregunta se desarrolla en esta conferencia, la cual tiene el objetivo de mostrar el impacto de este ambiente en la enseñanza y el aprendizaje de la geometría, mediante la posibilidad de acceder a la estructura de los objetos geométricos, gracias a las prácticas de construir y de deconstruir, movilizadas en los Ambientes de Geometría Dinámica, como GeoGebra. La práctica de construir implica que todos los objetos geométricos deben ser elaborados mediante un proceso de construcción que vaya determinando su estructura geométrica. Mientras que la práctica de deconstruir implica que los objetos geométricos tiene un comportamiento dinámico, el cual permite acceder a su estructura a través de la exploración y conjeturación. La presentación de estas prácticas se realiza a través de ejemplos con GeoGebra que el o la asistente a la conferencia puede realizar en vivo.
