Mª Antonieta Rodriguez - Olivia Scholz Marbán - Sergio Rubio Pizzorno
martes 31 de mayo, 2016
www.zergiorubio.org
Estructura de los Elementos de Euclides

Problematización del Saber matemático
Organización

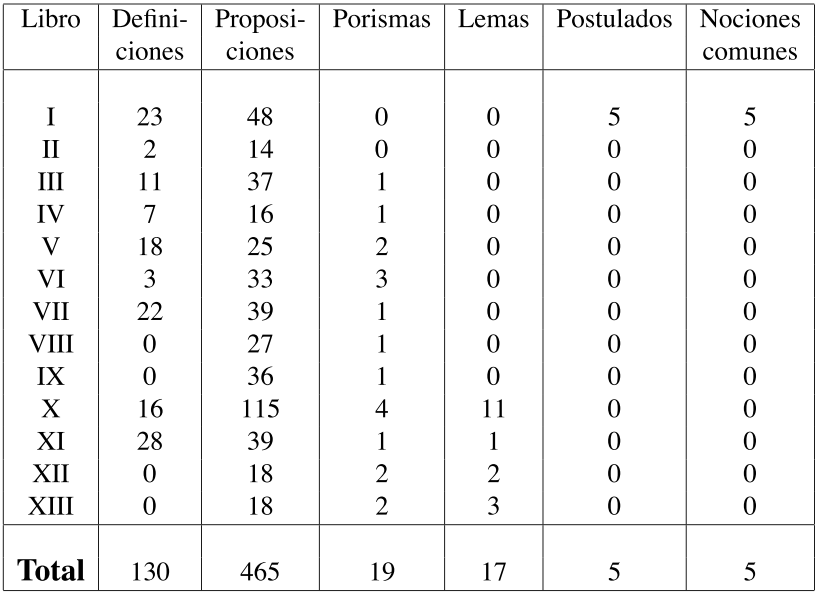
Navarro (2005, p. 52)
Definiciones

Una definición es una frase que sirve para introducir un concepto matemático. En ella, normalmente, se define la nueva noción relacionando unos términos más generales ya definidos.
¿Qué hace?
Introduce un (nuevo) concepto matemático.
¿Cómo lo hace?
A partir de relacionar términos más generales ya definidos.
Definición 24 (Zamorano, 1576)

Otra de las figuras de tres lados, triángulo equilátero es el que se contiene debajo de tres lados iguales. (folio 10-I)
| 21. Figura de tres lados | Figuras de tres lados son las contenidas debajo de tres líneas rectas. |
| 20. Figura rectilínea | Figuras rectilíneas son las que son contenidas de líneas rectas. |
| 14. Figura | Figura es la que es contenida de alguno de tus términos. |
| 13. Término | Término es, lo que es fin de cada cosa*. |
| 4. Línea recta | Línea recta es la que igualmente está entre sus puntos. |
| 3. Términos de la línea | Los términos de la línea son puntos. |
| 2. Línea | La línea es longitud que no se puede ensanchar. |
| 1. Punto | Punto es, cuya parte no es ninguna. |
Definición 24 (Zamorano, 1576)

Figura de tres lados
Lados iguales
Triángulo equilátero
Relaciona términos generales ya definidos.
Postulados y Nociones comunes
(Peticiones y Comunes sentencias)

Tanto las Peticiones y Comunes sentencias, son propiedades de los objetos matemáticos que se aceptan sin discusión.
Postulados y Nociones comunes
(Peticiones y Comunes sentencias)

La diferencia radica en que, las Comunes sentencias (nociones comunes o axiomas) son afirmaciones generales, válidas en todas las ciencias.
En cambio, las Peticiones (o postulados) son propiedades específicas de la Geometría, no tan evidentes. Debido a esto, se pide que se acepten.
Postulados y Nociones comunes
(Peticiones y Comunes sentencias)

Común sentencia
1. Cosas que a una misma son iguales, entre sí son iguales.
Petición
1. Tirar una línea recta desde cualquier punto hasta cualquier punto.
No es exclusivo de la matemática o geometría.
Propiedad geométrica.
Proposiciones

Afirmaciones que se logran demostrar partiendo de las proposiciones anteriores, las reglas aceptadas en las comunes sentencias y peticiones, y las propiedades que se suponen en las definiciones.
Proposiciones

Teoremas
Problemas
Indican propiedades de los objetos matemáticos.
..."lo cual convino hacerse."
Explica cómo se construyen los objetos matemáticos.
La definición de un objeto
matemático no implica su existencia, la construcción sí (Def. 24 y Prop. 1).
..."lo cual convino demostrarse".
Partes de las Proposiciones

| Enunciado | Frase en la que se declara lo que se quiere demostrar o lo que se quiere construir. |
| Exposición | Apartado en el que se concretan los datos del enunciado en un dibujo o se exponen los objetos que van a intervenir en los pasos posteriores. |
| Especificación | Frase en la que se concretan las condiciones que deben cumplir los datos del enunciado. |
| Construcción | Parte en la que se completa el dibujo añadiéndole las líneas o circunferencias que se necesiten para poder demostrar la afirmación del enunciado. |
| Prueba | Apartado dedicado a justificar los pasos lógicos necesarios para deducir la tesis buscada o para construir la figura deseada a partir de los resultados anteriores. |
| Conclusión | Último párrafo de la proposición. En él se repite la parte del enunciado que indica lo que se quería lograr. |
Proposición 1 Problema 1

Sobre una línea recta dada terminada hacer un triángulo equilátero.
Sea la línea recta dada terminada AP, conviene describir sobre AB un triángulo equilátero.
Sobre el centro A y según el espacio AB, descríbase el círculo BCD (por la tercera petición). Y también (por la misma) sobre el centro B y en el espacio BA descríbase el otro círculo ACE. Y (por la primera petición) desde el punto C, donde los círculos se cortan, tírese las líneas rectas CA y CB hasta los punto A y B.
Y porque el punto A es centro del círculo CBD será igual la línea AC a la línea AB (por la decima quinta definición). Y porque el punto B es el centro del círculo CAE será igual la línea BC a la línea AB. Luego ambas, CA y CB, son iguales a la línea AB, y cosas que a una son iguales, entre sí son iguales (por la primera común sentencia), luego la línea AC es igual a la línea CB. Luego las tres líneas CA, AB y BC son iguales entre sí.
Será pues equilátero el triángulo ABC y fabricado sobre la línea recta dada terminada AB, lo cual convino hacerse.
Enunciado
Exposición
Construcción
Prueba
Conclusión
Propuesta

Proposiciones que causaron dudas sobre sus elementos constituyentes la semana pasada, fue la proposición 20, puesto que para demostrar la relación general, Euclides demuestra tres relaciones particulares. Se estaba proponiendo la semana pasada, que esas proposiciones tenían especificaciones, pero según Navarro no es cierto, ya que sólo las proposiciones que tienen "pero..." en su enunciado poseen especificaciones.
Por lo tanto, hay proposiciones que para realizar la demostración general, se valen de demostrar relaciones particulares, sin que tengan especificaciones como uno de sus elementos constituyentes.
Proposición 25 Teorema 16

Si dos triángulos tuvieren los dos lados iguales a los dos lados el uno al otro:
Pero la base mayor que la base, tendrá también el ángulo contenido de iguales líneas rectas, mayor que el ángulo.
Siendo dos triángulos ABC y DEZ, que tengan los dos lados AB y AC iguales a los dos lados DE y DZ, el uno al otro, esto es AB al mismo...
Digo que el ángulo BAC es mayor que el ángulo EDZ, porque sino, o es igual a él o menor que él...
Luego el ángulo BAC no es menor que el ángulo EDZ y está demostrado que ni igual. Luego mayor es el ángulo BAC que el ángulo EDZ.
Luego si dos triángulos tuvieren y lo que se sigue, como en el teorema que convino demostrar.
Enunciado
Exposición
Construcción
Prueba
Conclusión
Especificación
Proposición 20 Teorema 13
Los dos lados de todo triángulo, tomados de cualquier manera, son mayores que el que resta.
Sea el triángulo ABC. Digo que los lados del mismo triángulo ABC son mayores que el que resta de cualquier manera que se tomen, es a saber, BA, AC mayores que BC y BC, AB que AC y BC, CA que el mismo AB.
Tiéndase (por la 2 petición) BA, hasta el punto D y (por la 2da proposición) póngase, AD igual a la AC y tírese DC. Pues porque DA es igual a la AC, es igual el ángulo ADC (por la 5ta proposición) al ángulo ACD y el ángulo BCD es mayor que el ángulo ACD.
Luego el ángulo BCD es mayor que el ángulo ADC y porque es el triángulo DCB que tiene el mayor ángulo BCD que el ángulo ADC y al mayor ángulo se le extiende mayor lado (por la 18 proposición).
Luego DB es mayor que BC pues igual DB a las dos AC, AB luego mayores a los dos lados BA, AC que el mismo BC.
De la misma forma demostraremos que también los lados AB, BC son mayores que CA y también BC, CA que AB.
Luego los dos lados de todo triángulo tomados en cualquier manera son mayores que el que resta, lo cual convino demostrarse.
Enunciado
Exposición
Construcción
Prueba
Conclusión
general
Conclusión
particular
Generalización

Teoremas e Inversos
Euclides realiza, cuando puede, una inversión de inferencias, es decir, estudia cuándo el resultado de un teorema se puede invertir, obteniendo el teorema inverso.
| Teorema | Teorema inverso |
|---|---|
| 5 | 6 |
| 13 | 14 |
| 18 | 19 |
| 24 | 25 |
| 27 | 29 |
| 47 | 48 |

P. 18 El mayor lado de todo triángulo se extiende debajo del mayor ángulo.
P. 19 Debajo del mayor ángulo de todo triángulo se extiende el mayor lado.
González, P. La historia de la matemática como recurso didáctico e instrumento de integración cultural de la Matemática
Porismas y Corolarios

Conclusión interesante que se deduce de una proposición demostrada pero que no es necesaria para el desarrollo posterior del libro.
Lemas

Son teoremas que se suponen como ciertos al demostrar una proposición, pero que una vez probada ésta se deben demostrar a su vez.
Es decir, son afirmaciones que si se justificaran por completo cuando se emplean en una demostración harían perder el hilo del razonamiento general.
¿PREGUNTAS?
Estructura de los Elementos de Euclides
By Sergio Rubio-Pizzorno
Estructura de los Elementos de Euclides
Análisis de la estructura de los Elementos de Euclides, cuidando sus partes constituyentes, tales como definiciones, proposiciones, porismas, lemas, postulados y nociones comunes.
- 2,304


