後綴
蕭梓宏
理想的上課方式
1.定義
2.性質
2.作法
3.應用
後綴
\(suf_i\)代表由第\(i\)個字元開始的後綴
Suffix Array
\(SA\)
把後綴照字典序排序的陣列
字典序第\(i\)小的後綴是\(suf_{SA[i]}\)
\(rank\)
\(SA^{-1}\)?
\(suf_i\)的字典序是第\(rank[i]\)小
\(abbaa\)
\(a\)
\(aa\)
\(abbaa\)
\(baa\)
\(bbaa\)
\(5\)
\(4\)
\(1\)
\(3\)
\(2\)
\(abbaa\)
\(bbaa\)
\(baa\)
\(aa\)
\(a\)
\(3\)
\(5\)
\(4\)
\(2\)
\(1\)
作法
倍增囉
w = 1,2,4,8......
for(w = 1;w < n;w<<=1){
sort(sa + 1, sa + n + 1, [](int x, int y) {
return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];
});
memcpy(oldrk, rk, sizeof(rk));
for (p = 0, i = 1; i <= n; ++i) {
if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
rk[sa[i]] = p;
} else {
rk[sa[i]] = ++p;
}
}
}
太慢了?
夠了ㄅ
慢慢來比較快
觀察
其實每次sort 都是在比兩個東西而已?
而且那兩個東西都介於1到 n?
所以其實我們要排序的後綴就可以視為要排序一些\(N\)進位的二位數
s = 0;
for(i = n-w+1;i <= n;i++) temp[s++] = i;//what is temp?
for(i = 1;i <=n ;i++)
if(sa[i] > w)
temp[s++] = sa[i]-w;
memset(cnt,0,sizeof(cnt));
for(i = 1;i <= n;i++) cnt[oldrk[i]]++;
for(i = 1;i < m;i++) cnt[i] += cnt[i-1];//what is m?
for(i = n;i > 0;i--) sa[--cnt[oldrk[i]]] = i;
for (p = 0, i = 1; i <= n; ++i) {
if (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
rk[sa[i]] = p;
} else {
rk[sa[i]] = ++p;
}
}//same用處
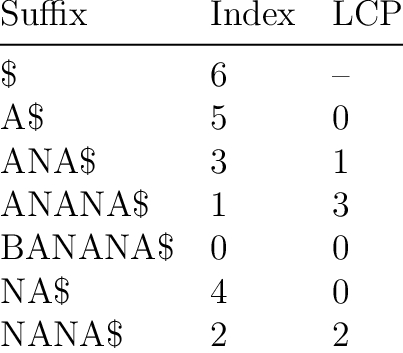
lcp
\(lcp[i]\)代表\(suf_{SA[i]}\)和\(suf_{SA[i+1]}\)的最長前綴的長度
作法
從\(suf_1\)的lcp算到\(suf_n\)的lcp
*\(suf_i\)的lcp指的是\(lcp[rank[i]]\)喔!
作法
for(int i=1; i<=n; i++, k?k--:0)
{
if(rank[i]==n) {k=0; continue;}
int j=sa[rank[i]+1];
while(i+k<=n && j+k<=n && s[i+k]==s[j+k])
k++;
lcp[rank[i]]=k;
}用處
複選pA
\(lcp(suf_{SA[l]},suf_{SA[l+1]},...,suf_{SA[r]})\)
\(min(lcp[l],lcp[l+1],...,lcp[r-1])\)
=
CT
SAM
定義
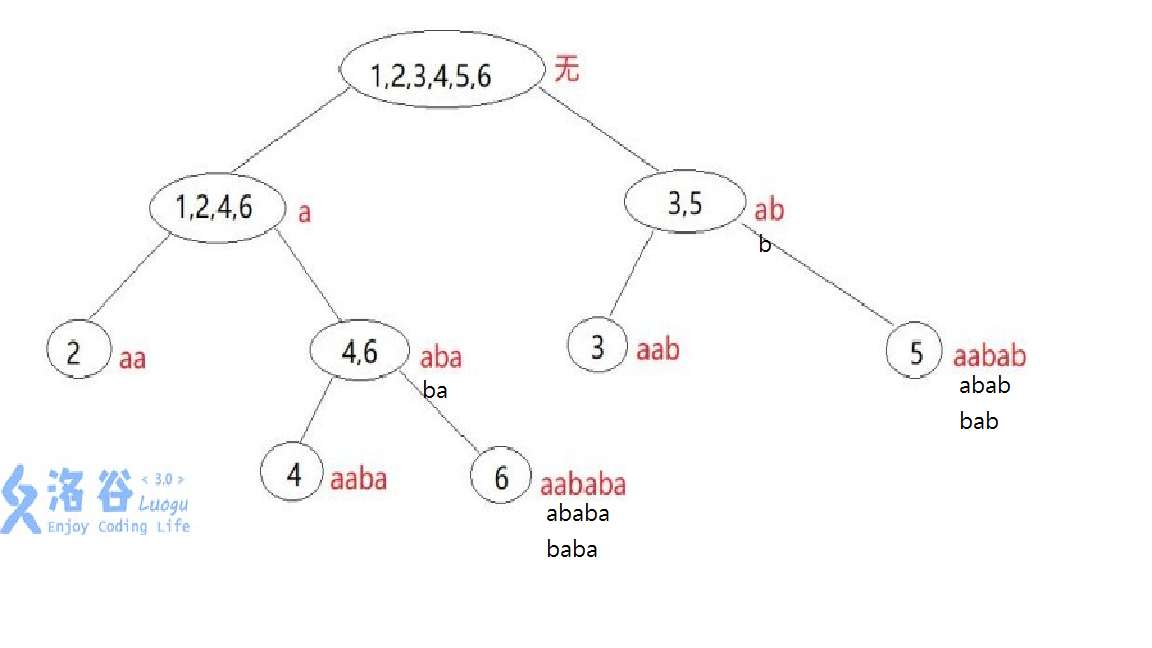
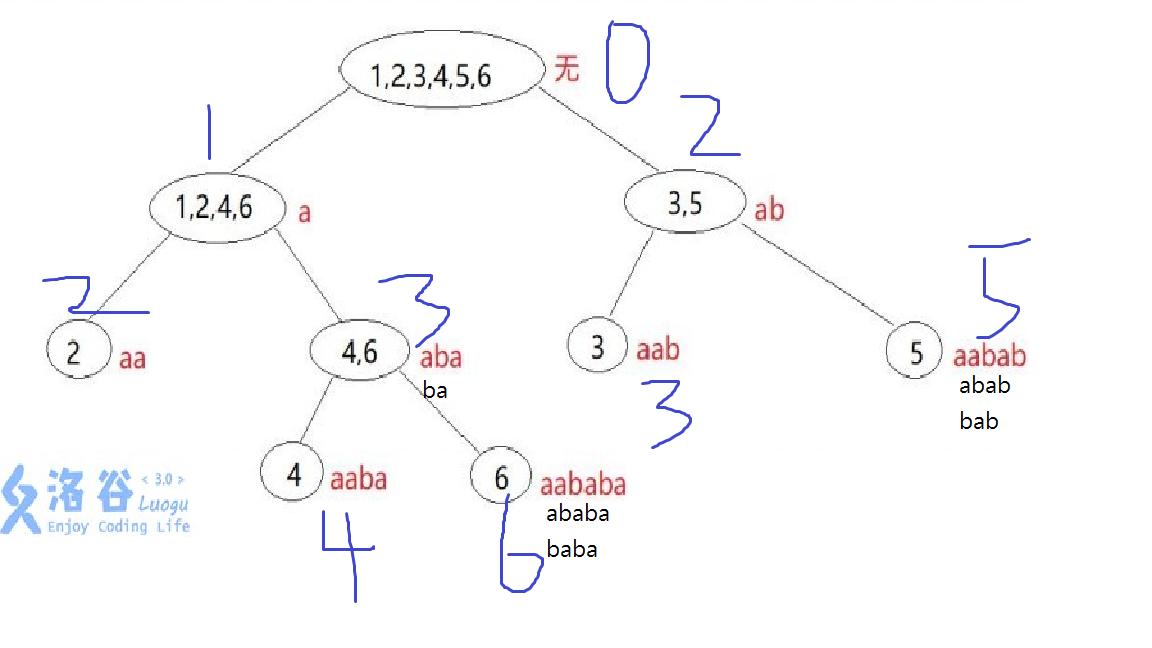
對於一個\(T\)的子字串\(s\)
\(endpos(s)\):\(s\)在\(T\)中出現位置結尾形成的集合
T = aabab
\(endpos("ab") = \{3,5\}\)
\(aababa\)
parent tree
How many nodes?
len
fa
\(aababa\)
SAM
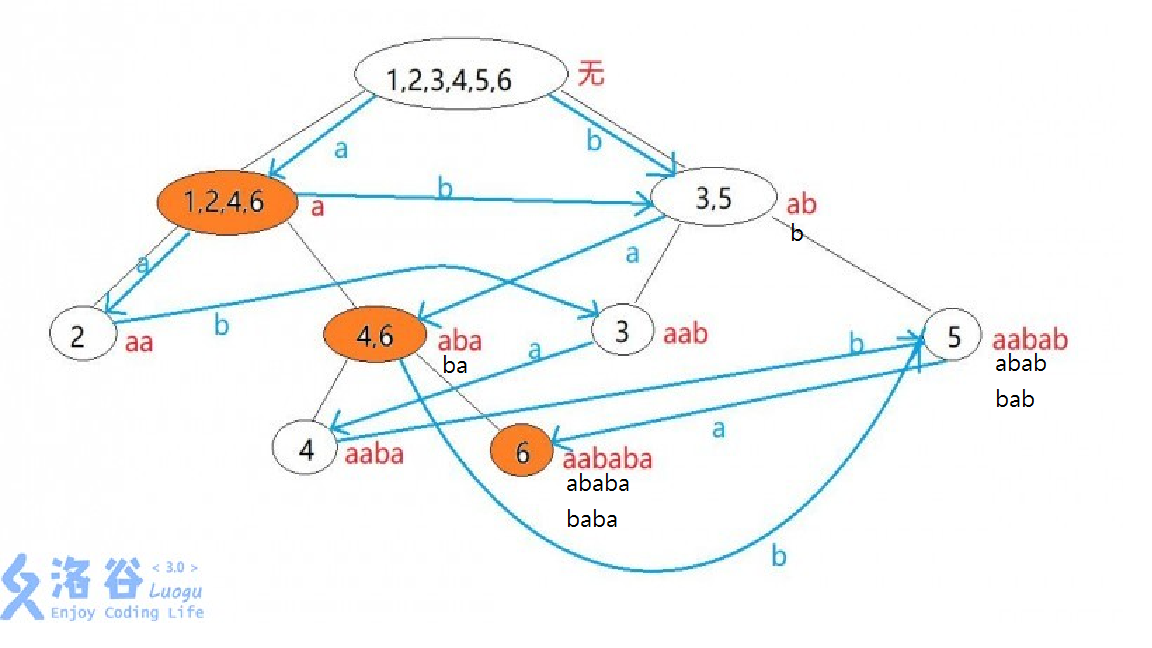
How many edges?
樹邊\(\to\)2n-2
非樹邊\(\to\)n-1(對應後綴)
struct NODE
{
int ch[26];
int len,fa;
NODE(){memset(ch,0,sizeof(ch));len=0;}
}dian[MAXN<<1];投票
建法
一個字元一個字元加
新增一個字元\(c\)時
1.新增一個節點\(cur\)代表目前的整個字串(整串)
2.從\(last\)一直跳\(fa\),沒有\(c\)的出邊就連一條到\(cur\),直到有(假設是\(p\))或到根
3.設\(p\overset{c}\to q\),若\(len(q) == len(p) +1\),\(fa(cur) = q\)。結束
4.要不然把\(q\)複製(叫做\(nq\)),但\(len(nq)=len(p)+1\),把\(q\)、\(cur\)的\(fa\)設成\(nq\)
5.從\(p\)繼續跳\(fa\),有\(c\)的出邊到\(q\)就改連到\(nq\),直到不是
建法
1.整串
2.回連
3.長度要連續
4.nq當爸爸
5.回改
示範
\(aaba\)
換你們
one step one step come
\(aababa\)
討論時間
提問很重要
一個字元一個字元加
新增一個字元\(c\)時
1.新增一個節點\(cur\)代表目前的整個字串(整串)
2.從\(last\)一直跳\(fa\),沒有\(c\)的出邊就連一條到\(cur\),直到有(假設是\(p\))或到根
3.設\(p\overset{c}\to q\),若\(len(q) == len(p) +1\),\(fa(cur) = q\)。結束
4.要不然把\(q\)複製(叫做\(nq\)),但\(len(nq)=len(p)+1\),把\(q\)、\(cur\)的\(fa\)設成\(nq\)
5.從\(p\)繼續跳\(fa\),有\(c\)的出邊到\(q\)就改連到\(nq\),直到不是
code
void add(int c)
{
int p=las;int np=las=++tot;
dian[np].len=dian[p].len+1;
for(;p&&!dian[p].ch[c];p=dian[p].fa)dian[p].ch[c]=np;
if(!p)dian[np].fa=1;
else
{
int q=dian[p].ch[c];
if(dian[q].len==dian[p].len+1)dian[np].fa=q;
else
{
int nq=++tot;dian[nq]=dian[q];
dian[nq].len=dian[p].len+1;
dian[q].fa=dian[np].fa=nq;
for(;p&&dian[p].ch[c]==q;p=dian[p].fa)dian[p].ch[c]=nq;
}
}
}副砸肚?
for(;p&&dian[p].ch[c]==q;p=dian[p].fa)dian[p].ch[c]=nq;(從\(p\)繼續跳\(fa\),有\(c\)的出邊到\(q\)就改連到\(nq\),直到不是)
(假設經過的是\(p_1,p_2,\cdots,p_n\))
\(minlen(fa(last)) \geq minlen(p_1) > minlen(p_2) > \cdots > minlen(p_n) = minlen(nq)-1 = minlen(fa(cur))-1\)
經典應用
1.相異子字串數
3.smallest cyclic shift
5.最短不出現字串
錫堤
來源
deck
By Zi-Hong Xiao
deck
- 1,185



