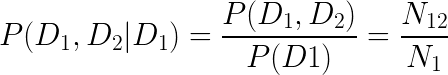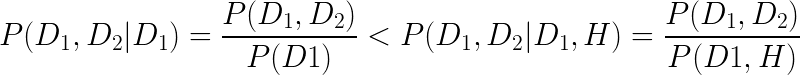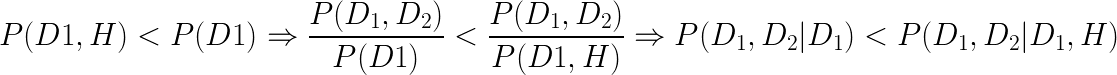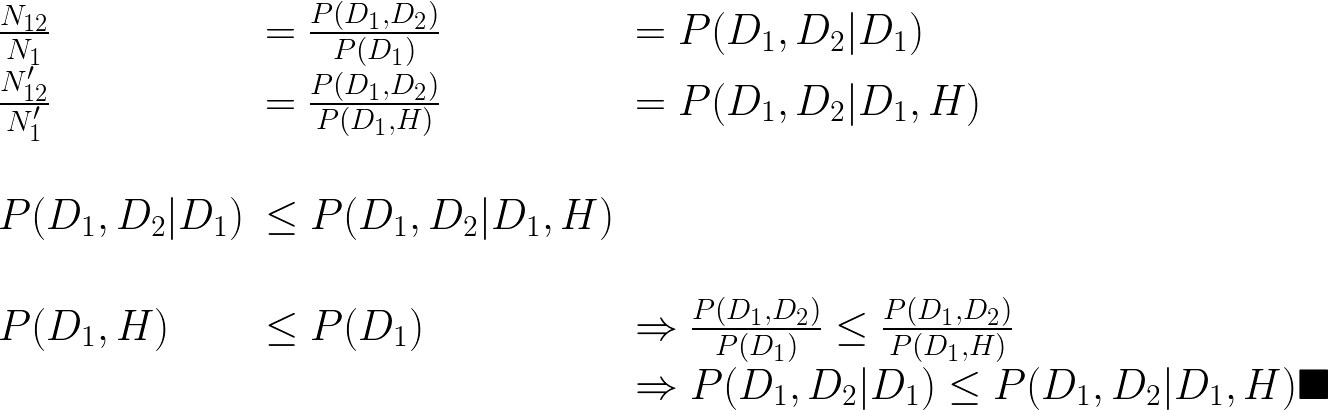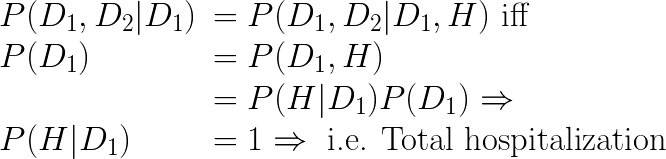Outline
- Bias & Selection bias
- Consequences of selection bias
- Causal representation of different biases
- eQTL
- PCA adjustment in eQTL
- Bias for PCA adjustment
Detecting, Quantifying and Correcting Selection Bias due to PCA adjustment in eQTL discovery
Alex Couto Alves
Bias vs Noise
-
Systematic Error (Bias): Systematic difference between population parameter and the estimated statistics.
-
Random Error (Noise): Random difference between population parameter and the estimated statistics.
Nomenclature
-
Selection Bias
-
Collider bias
-
Berkson bias
Does gallstones cause diabetes?
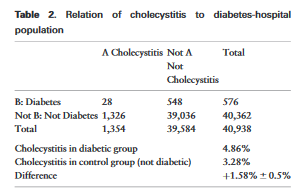
Ratio of multiple diagnosis to single diagnosis in the hospital is always greater than in the general population
"
Selection bias
D1
H
D2
A causal model
E
G
Suppression & Selection Bias
PCA of gene expression
(Matthias Scholz, Ph.D. thesis)
PC1 = Weight11 * Expression Gene 1 + Weight12 * Expression Gene 2 + …
PC2 = Weight21 * Expression Gene 1 + Weight22 * Expression Gene 2 + …
Expression quantitative trait loci mapping
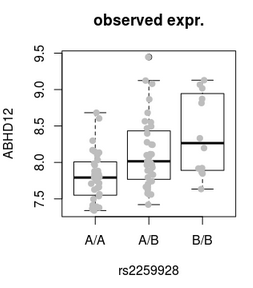
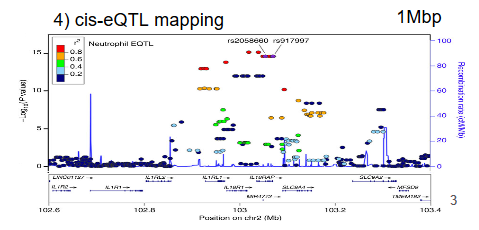
Adjustment for expression PCs increase the yield of cis-eQTLs
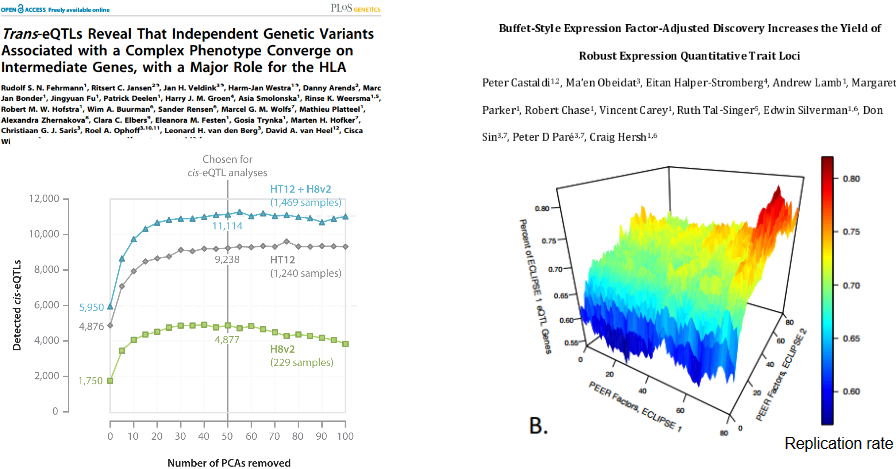
H
SNP
SNPt
Gt
G
S
B
PCA
?
S
Causation vs bias and confounding in genetic association studies
Detection of selection bias
- Increasing PCs increases numbers of replicable eQTLs
- PCs are functionally defined from expression
- eQTL associations adjusting for PC recapitulate selection bias causal structure
- Numerical simulations illustrate two types of selection bias
- Empirical assessments suggests effect sizes of some eQTLs are biased
Functional definition of Expression PC
Selection Bias & Endogeneity Bias
PCA selection bias
D1
H
D2
A causal model
E2
E1
G1
PC1
G2
SNP2
SNP1
Gg
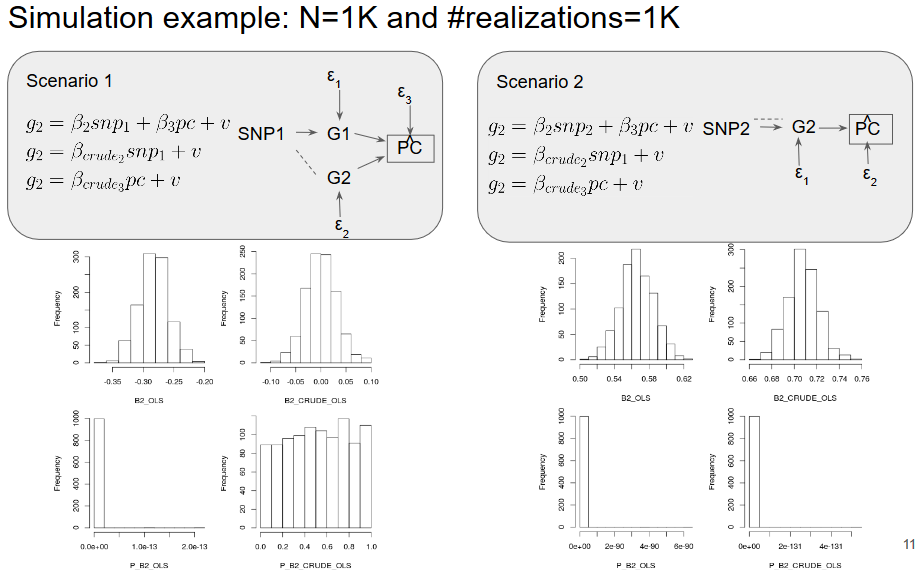
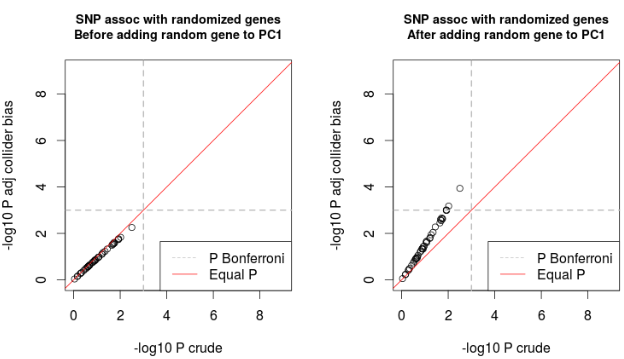
Simulation PCA Selection Bias
Empirical assessment
Empirical assessment
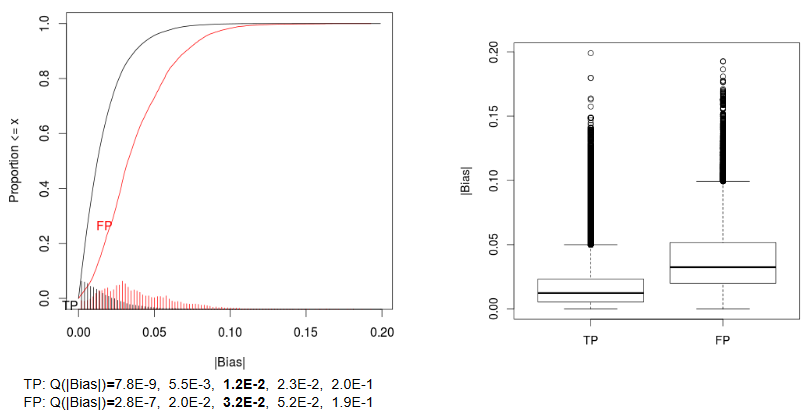
Quantification of Selection Bias
- GWAS assumptions excludes confounder bias
- Mathematical analysis of the regression coefficients estimates reveals bias factor is independent of the genetic effect
- Construction of a null model of no genetic effect shows the possibility of FP induced by bias alone
- Construction of a test statistic corrected for the biases on effect size and SE estimates
- Principled detection of putative true & false positives
- Quantification of the FP and FN due to selection bias
selection bias in the regression coefficients estimates
A null model of no genetic effect
(Betas induced by Selection Bias)
A test for regression coefficients adjusting for selection bias and suppression
Principled definition of TP/FP
Significant associations with null genetic effect
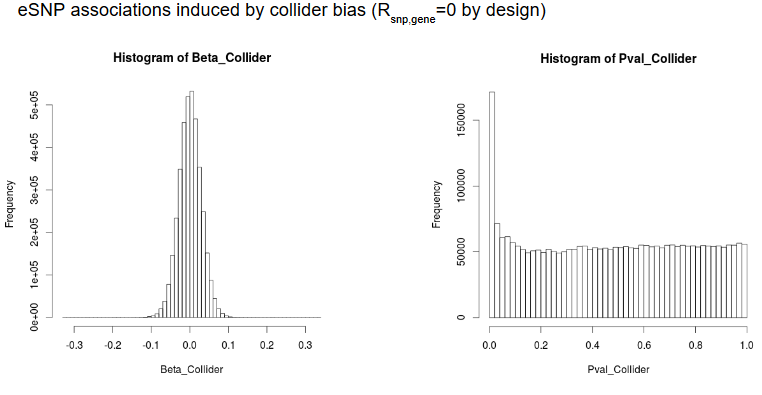
Bias-induced FP/FN
Fat expression
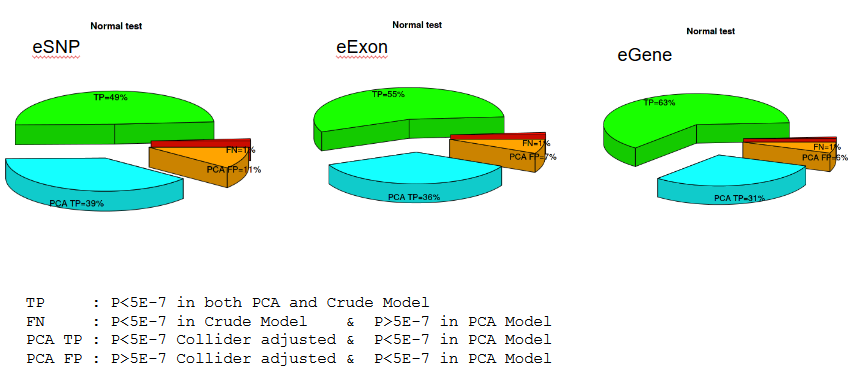
Bias-induced FP/FN
LCL expression
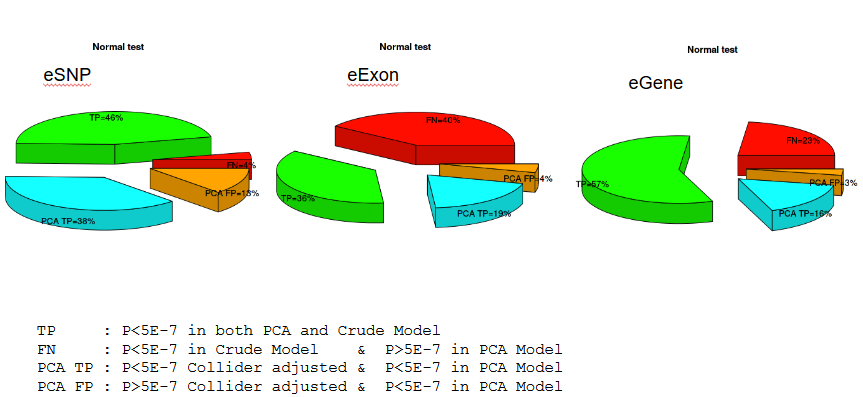
Correction of Selection Bias
- Randomization of real data assesses bias correction validity
- P-values corrected for bias are validated against the null of no genetic effect with and without PC-induced selection bias
- Betas adjusted for bias are validated against the null of no genetic effect
Design of the experiment
Correction of selection bias
P-values
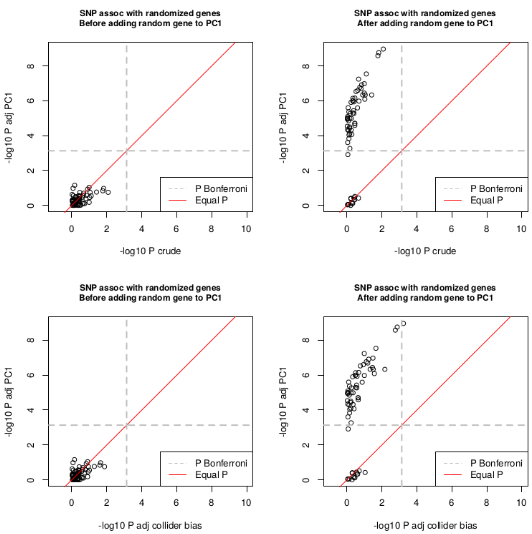
Confounding in genetic associations
Crude and PC adjusted models
Confounding
LCL
| 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||
| 3 |
Genotypes
| 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||
Expression
SNP
? B1
G
B2
C
?
1M
317K
610K
Expression batch effects
Confounding analysis
Crude model
Confounding analysis
PC adjusted model
Artificial confounding
Emulating missing data impution to ref
SNP
B1
G
B2
C
Genotypes
Expression
Artificial confounding
Crude model
Artificial confounding
PC adjusted model
Conclusion
- Models with adjustment for expression PCs explain variation on Y using variation on Y
- This causes endogeneity biases, including selection bias and suppression.
- Correction of selection bias in genetic studies is possible because of knowledge of the theoretical causal model and the assumption of no confounding
- It is possible to mitigate confounding in properly designed genetic association studies.
- Violations to the assumption of no confounding, can severely affect both PC-adjusted and crude model estimates, but less so in PC-adjusted models
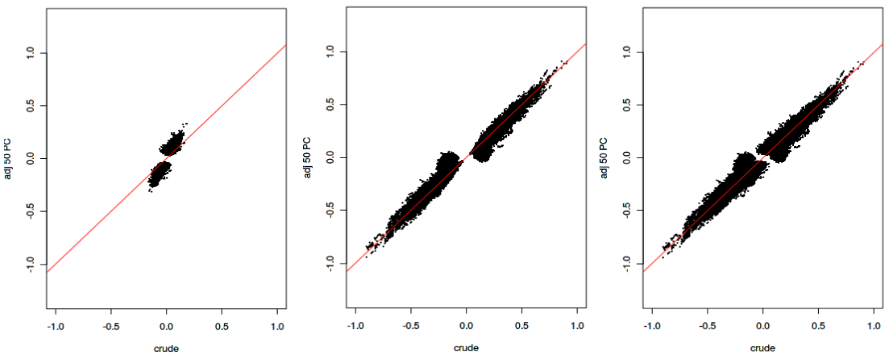
Correction of selection bias
Beta values
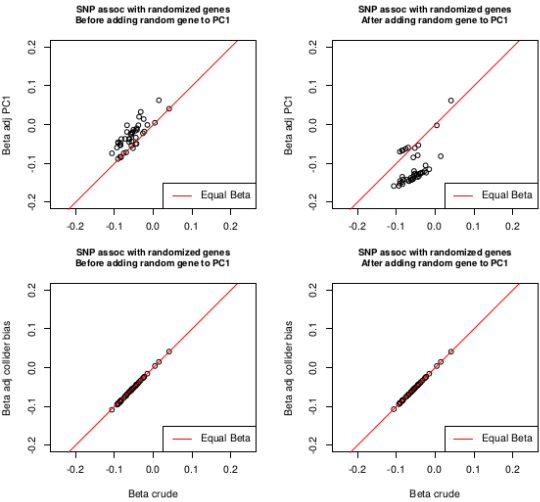
Correction of selection bias
P-values
Empirical assessment
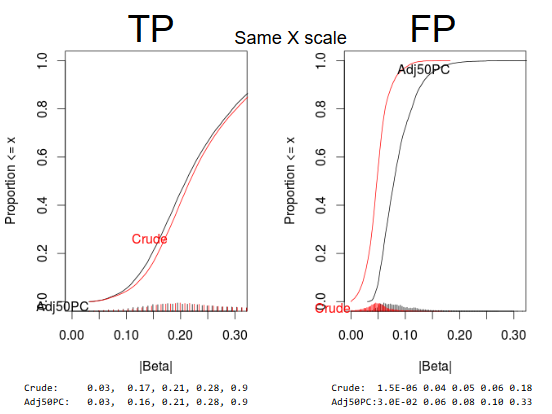
Empirical assessment
FP
TP
All
Basic causal structures
X
Y
- C
- X
- Y
- C
Confounder
- X
- Y
- C
- X
- Y
- C
Collider
X
Y
- M
- X
- Y
- M
Mediator
- X
- Y
- E
- X
- Y
- E
Exogenous variable
Does the causes of gallstones cause diabetes?
- E
- D1
- D2
- H
- G
- E
- D1
- D2
- H
- G
- D1
- D2
- H
Joseph Berkson (1899 – 1982)
- 1922 M.A. Physics, Columbia
- 1927 M.D., Johns Hopkins
- 1928 Dr.Sc., Johns Hopkins
- 1933 Head of Biometry and Medical Statistics ,Mayo Clinic
- 1946 Legion of Honour, US War Dept
From Biometrics Vol. 39, No. 4 (Dec., 1983), pp. 1107-1111
D1
H
D2
D1
H
D2
A B
Identities
Selection bias
- Only total hospitalization avoids Berkson bias:
Outline Bias & Selection bias Consequences of selection bias Causal representation of different biases eQTL PCA adjustment in eQTL Bias for PCA adjustment
pcabias
By acoutoal
pcabias
Detecting, Quantifying and Correcting Selection Bias due to PCA adjustment in eQTL studies
- 635
