Algorytmy kwantowe
Czyli skąd ten dreszczyk emocji...
Adam Glos
Instytut Informatyki Teoretycznej i Stosowanej Polskiej Akademii Nauk, Gliwice
QWorld
Po co te kwantowe komputery?
- Problemy które próbujemy rozwiązać stają się coraz "większe"
- Możemy próbować rozwiązać je na kilka sposobów
- tworzyć lepsze algorytmy
- tworzyć mocniejsze procesory/karty graficzne
- łączyć jednostki obliczeniowe (obliczenia wielowątkowe)
Wszystkie metody mają swoje limity!
Jak zmierzyć jakość algorytmu?
Załóżmy, że mamy dane rozmiaru n. Ile więcej czasu będziemy potrzebować jeśli będziemy mieli dwukrotnie większe dane (2n)?
T_1(n) = n: \quad \frac{T_1(2n)}{T_1(n)} = \frac{2n}{n} = 2
T_2(n) = n^2: \quad\frac{T_2(2n)}{T_2(n)} = \frac{(2n)^2}{n^2} = 4
T_3(n) = \sqrt n: \quad\frac{T_3(2n)}{T_3(n)} = \frac{\sqrt{2n}}{\sqrt{n}} = \sqrt 2
<- dziwna sytuacja!
T_4(n) = 2^n: \quad\frac{T_4(2n)}{T_4(n)} = \frac{2^{2n}}{2^n} = \frac{(2^{n})^2}{2^n} = 2^n
bardzo źle! ->
Jak zmierzyć jakość algorytmu?
Czy T(n) jest istotnie wolniejsze niż S(n)?
T(n) = 2n\qquad S(n) = n
Będziemy pisać, że T(n)=O(n)
Uwaga #1: 0.0001n = O(n) oraz 1000n=O(n)
Uwaga: n+n^2=O(n^2)
Deutsch-Jozsa
010...11
Czarna skrzynka
0
- Skrzynka przyjmuje ciągi 0-1 ustalonej długości n i zwraca bit 0 lub 1
- Skrzynka którą dostajemy albo:
- stała
- zbalansowana
Czarna skrzynka
Czarna skrzynka
Deutsch-Jozsa
010...11
Czarna skrzynka
0
Klasycznie
- Możemy jedynie wrzucać różne ciągi długości n (własność czarnej skrzynki!)
- Jeśli znajdziemy dwa różne ciągi, które zwrócą odpowiednio 0 oraz 1, to skrzynka jest zbalansowana
- jeśli dla 2^{n-1}+1 otrzymamy tę samą wartość - stała
W najgorszym przypadku:
2^{n-1}+1=O(2^n)
zapytań!
Kwantowa czarna skrzynka
00
Czarna skrzynka
0
01
Czarna skrzynka
1
10
Czarna skrzynka
0
11
Czarna skrzynka
1
Kwantowa czarna skrzynka
|00\rangle
|01\rangle
|10\rangle
|00\rangle
|11\rangle
|0\rangle
|1\rangle
|0\rangle
|1\rangle
Powiniśmy mieć tylko samo kubitów na wejściu i wyjściu!
Kwantowa czarna skrzynka
|00\, 0\rangle
Pierwsze dwa qubity bez zmian.
Na ostatnim qubicie:
- jeśli wynik miał być 1 - zrób negację
- w przeciwnym wypadku nie rób nic
|00\, 0\rangle
|00\, 1\rangle
|00\, 0\rangle
|01\, 0\rangle
|01\, 1\rangle
|01\, 1\rangle
|01\, 0\rangle
|10\, 0\rangle
|10\, 0\rangle
|10\, 1\rangle
|10\, 1\rangle
|11\, 0\rangle
|11\, 1\rangle
|11\, 1\rangle
|11\, 0\rangle
|01\, 1\rangle +|00\, 0\rangle
|01\, 0\rangle +|00\, 0\rangle
Mamy kwantową bramkę - działa na superpozycji!
Algorytm Deutsch-Jozsa
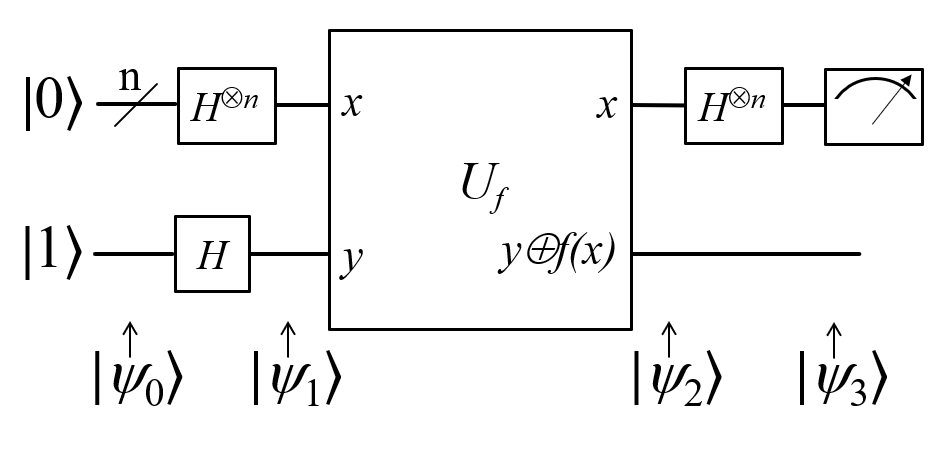
- Jeśli na pierwszych n kubitach zmierzymy 00...0, to funkcja jest stała (zawsze 0 lub 1)
- jeśli nie zmierzymy 00...0, to funkcja jest zbalansowana
Dowód na wiki
Wystarczy zapytać raz!
Czyli koniec, wygraliśmy?
Wyrocznia
1.
2.
3.
\vdots
\vdots
(k-1).
k.
(k+1).
(n-2).
(n-1).
n.
- Wyrocznia wie który element jest wyróżniony
- wyrocznia odpowiada "tak"/"nie"
Klasyczna wyrocznia
Jak działa klasyczny świat:
- Ustalamy jakąś kolejność elementów i pytamy po kolei
-
Średnio potrzebujemy≈ n/2=O(n)zapytań!
Klasyczna wyrocznia
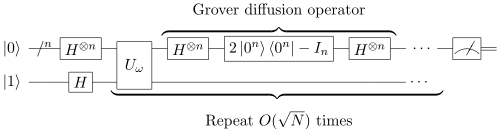
Musimy powtórzyć fragment
\frac{\pi}{4}\sqrt N
razy!
Czy sqrt(N) to dużo?
| n | kwantowo pi sqrt(N)/4 | klasycznie n/2 |
|---|---|---|
| 10 | 2.5 sekundy | 5 sekund |
| 1000 | 25 sekund | 8.4 minuty |
| 100 000 | 4.1 minuty | 14 godzin |
| 1000 000 | 13 minut | 5.8 dnia |
| 1000 000 000 | niecałe 7 godzin | 1.5 roku |
... ale trudne problemy pozostają trudne!
Tak, różnica jest ogromna...
P vs NP
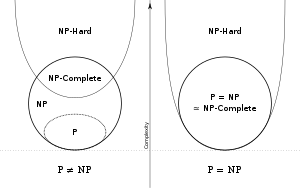
Czy istnieje kwantowy algorytm, który jest istotnie szybszy od (przynajmniej) znanych nam algorytmów?
Faktoryzacja liczb!
a, b - duże liczby (tysiące cyfr)
- obliczenie a*b jest banalnie proste
- Jeśli mamy n = a*b, to znalezienie a i b może być bardzo trudne!
Algorytm Shora rozwiązuje to w czasnie O(d^3), gdzie d jest liczbą cyfr!
Czy to koniec?
Nie, faktoryzacja nie jest NP-trudna (chyba)
Nie, komputery kwantowe są zbyt małe - mamy kilkadziesiąt kubitów , potrzebujemy miliony
Czy to wszystkie algorytmy?
Shor
Deutsch-Jozsa
Grover
Variational Quantum Eigensolver
Quantum Machine Learning
Simon
Quantum annealing
Quantum Approximate Optimization Algorithm
hybrid quantum-dynamic algorithms
On Quantum Algorithm zoo there is over 60 algorithms!
Ultimate goal: help us creating a new one!
https://quantumalgorithmzoo.org/
Komputery kwantowe
By Adam Glos
