基礎算法

  • 演算法介紹 Intro

  • 複雜度分析 Complexity

  • 排序 Sort
  • 二分搜 Binary Search
  • 遞迴 Recursion
  • 分治 Divide and Conquer
  • 動態規劃 Dynamic Programming
  • 貪婪 Greedy
  • STL Library

目錄

一連串指令用以解決特定問題

aka. 解決問題的思維

演算法 algorithm

ex:最大公因數的短除法和輾轉相除法流程不一樣

Complexity

d = 0
for i in range(n):
	d += 1

#1

d = 0
for i in range(n):
	for j in range(n):
    	d += 1

#2

n=10 N=100 N=1000 N=10000
#1 10 100 10^3 10^4
#2 100 10000 10^6 10^8

As N gets larger, the difference in efficiency increases

A "complexity" of a program is to express the efficiency when the data that the program has to process becomes very big.

...

Time Complexity

  • The "growth trend" of a program's efficiency
  • Program #1's growth trend is \(N\), whilst #2 is \(N^2\)

Big-O Notation

A notation to express a approximate complexity using algebraic terms.

For a growth trend of f(x), the complexity is O( f(x) )

Attributes：

1. Big-O represents the upper bound of a program complexity, which we ignore the less complex growth trend. Ex: If one part of a program has a growth trend of \(N\), another is \(N^2\), the complexity is \(O(n^2)\)

2. If a part of program doesn't contribute to the growth trend, or doesn't get effected by the data size, then it is not considered in Big-O. Ex: N, 2*N, N+1000 have all the same growth trend, which is N, so the notation is \(O(N)\)

Constant

"If a part of program doesn't contribute to the growth trend, then it is not considered in Big-O."

 

The parts where we ignored is called "constant", although it is not part of the Big-O, it should still considered in practicality.

 

Ex: Although the complexity of the remainder calculation(%) and addition calculation(+) both are O(1), in reality % is much slower than +, and could be easily manifested.

Space Complexity

The growth trend of the memory's usage.

Same thing as calculating time complexity, except we look for the parts where we declare variables and arrays.

Appendix: Correlation between complexity and data size

(assume the time limit is 1 ~ 2 seconds)

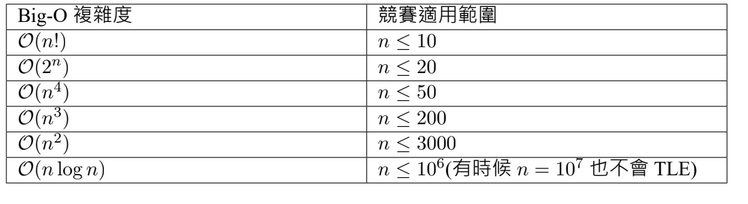
credit: ioncamp

Sort

Selection Sort

Keep finding the biggest number

\(O(n^2)\)

14

20

3

32

27

14

20

3

27

32

14

20

3

27

32

14

3

20

27

32

3

14

20

27

32

Bubble sort

Start from the end of the array, move the element rightward till the number to the right is bigger than you.

\(O(n^2)\)

32

20

3

14

27

20

32

3

14

27

20

3

32

14

27

20

3

14

32

27

20

3

14

27

32

Quick Sort

Choose a pivot number(can be any), then put the number smaller than the pivot on the left, bigger on the right, then repeat respectively with the left and right subarrays.

Best case \( O(n\log n) \)

Worst case \(O(n^2)\)

32

3

14

20

27

3

32

20

27

first split

32

27

14

20

14

3

second split

3

14

20

27

32

third split

3

14

20

27

32

done

Merge Sort

Keep splitting the array in half, then sort while you merge the two subarrays

\(O(n\log n)\)

32

20

3

14

27

32

20

3

14

27

32

20

3

14

27

3

14

20

27

32

14

27

3

14

20

32

20

32

3

14

27

Binary Search

終極密碼

First player think of a number in mind, the second player guesses the number. The first player has to tell if the number guessed is larger or smaller then the answer, until it guessed it.

Obvious tactic: narrowing the range, and that is essentially doing binary search.

Given a sorted increasing array, find whether the number k is in the array.

Example

go through every element: \(O(n)\), we can do better!

binary search: check the center element of the known range in the array, if the center element > k, that means k might be in in right. If center <k, then k might be in the left.

By doing this, we keep narrowing our range.

https://algorithm-visualizer.org/branch-and-bound/binary-search

If the current known range is [l, r], we check the element in the middle, which is at (l+r)/2

Binary Search

If k is larger, we set our known range to [mid, r], because every element of l~mid all <= mid, so couldn't =k

If k is smaller then set our range to [l, (l+r)/2], same reason.

Complexity: O(log n)

Explain: Assume we have N numbers in the original known range, every time we cut the range in half into n/2, do it again its (n/2)/2, so on until the range only have 1 element left.

 

n\times 2^{-x}=1 \\ \Rightarrow 2^{-x}=n^{-1} \\ \Rightarrow -x=-\log_2 n \\ \Rightarrow x=\log_2 n

Can we apply binary search when the array isn't sorted?

Monotonic

because our algorithm relies on the prediction that one side is always larger and another side is always smaller.

In conclusion, to binary search something(doesn't have to be an array of numbers), it needs to be monotonic. In other words, it needs to present a same growing trend on a continuous range.

nope

Binary search doesn't need to be on a array, can be anything monotonic.

Generalization

example: Assume in a problem, if the answer exists in condition k, and also exists in conditions >k, than the problem is monotonic.

基地台

easy solution: enumerate R from small to big, check every one of the them whether it works.

At a straight line there is N service spots, every cell tower can cover the service spots within a diameter of R.

Given the coordinates of the service spots and the number of cell towers K, question: what is the smallest R in order for the K cell towers to cover all N service spots? (every cell towers have the same diameter R and can be placed arbitrarily)

基地台

observation: the longer the diameter, the more it can cover(when always placed optimally)

AKA: if a diameter of R can let K cell towers cover all the spots, than every diameter greater than R can.

Monotonic !

Binary search: if the diameter mid is good, that means mid and >mid  all are good diameters, that also means >mid will never be the smallest available diameter, hence we can shrink our upper range to mid.

Implementation(c++)

check() function is to check whether diameter mid can cover all the spots.

int binary_search(){
  int l = 0;
  int r = n;

  while( l < r-1 ){
      int mid = ( l + r ) / 2;
      if(check(mid)){
          r = mid;
      }
      else{
          l = mid;
      }
  }

  return l;
 }
 
 
 
 
 //laialanorz

例題

二分搜尋法

雷射測試

真假子圖 - 難

掃地機器人 - 超級難，慎入

補充：三分搜

二分搜運用在一個呈現單調成長的序列上

但是如果要在呈現類似二次函數的序列上找最大(小)值呢?

目標(最小的f(x))

一樣設定一個左右界線L, R

示意：

取兩個中間值(一個中間靠右一個中間靠左)：mL, mR

怎麼縮小範圍?

考慮f(x)中，f(mL), f(mR)的大小關係

if f(mL)>f(mR)

兩種情況：

f(mL)

f(mR)

f(mL)

f(mR)

可以發現，最低點不可能出現在<ml的地方，因次可以把L=mL

怎麼縮小範圍?

if f(mL)<f(mR)

兩種情況：

f(mL)

f(mR)

f(mL)

f(mR)

最低點不可能出現在>mR的地方，因次可以把R=mR

怎麼取mL, mR?

不拘(不一定要三等分)

ex:

mR=(L+R)/2

mL=(L+mR)/2

複雜度：O(log n)

每次縮小範圍接近二分之一，所以乃為log n，但常數比二分搜大

範例實作(c++)

long double tenary_search(){
  long double l = -1e9, r = 1e9;
  while(r-l>1e-9){
      ll mr = (l + r) / 2.0;
      ll ml = (l + mr) / 2.0;
      if(check(ml) > check(mr)){
          l = ml;
      }
      else{
          r = mr;
      }
  }
  return l;
}

Recursion

Call yourself within the yourself

 

ex: Fibonacci Sequence f(x)=f(x-1)+f(x-2)

int fib(int x){
  if(x == 1) return 1;
  else if(x == 2) return 1;
  
  return fib(x-1) + fib(x-2);
}

A problem can be solved by recursion usually involves:

1. the problem can be split into subproblems

2. every subproblems can be solve similarily

輾轉相除法Euclidean Algorithm

gcd(a, b)=\left. \begin{cases} b, &\text{if }a=0 \\ gcd(b\%a, a) &\text{otherwise} \end{cases} \right\}
int gcd( int a, int b ){
    if(b == 0)
        return a;
    return gcd( b, a%b );
}

Tower of hanoi

Dissecting Problem

In order to move the bottom disk to C, first we have to move all the disks above it to B

algorithm:

1. move the top n-1 disks from A to B

2. move the n'th disk to C

3. move the n-1 disks from B to C

Dissecting Problem

lets replace A, B, C as START, HOLD, TARGET respectively

solve(N, START, HOLD, TARGET){

     solve(N-1, START, TARGET, HOLD)

     move disk N to TARGET

     solve(N-1, HOLD, START, TARGET)

}

solve(3, a, b, c)

call stack

solve(2, a, c, b)

solve(1, a, b, c)

solve(1, c, a, b)

solve(2, b, a, c)

solve(1, b, c, a)

solve(1, a, b, c)

Implementation

void solve(int n, char a, char b, char c){
  if(n==0) return;
  solve(n-1, a, c, b);
  printf("move ring %d form %c to %c", n, a, c);
  solve(n-1, b, a, c);
}

int main(){
  int n;
  n=4;
  solve(n, 'a', 'b', 'c');
}

Backtracking

cleverly trim down the depth of recursion by breaking recursion on certain cases

n-queens

例題

函數運算式求值

括號匹配

子集合的和

Divide and Qonquer

1. divide problem into subproblems

2. solve the subproblems

3. merge the subproblems

usually implemented by recursion

Example - Merge Sort

Keep dividing the sequence in half until the length is 1, from here we can O(n) merge two sorted sequences into their original sequence.

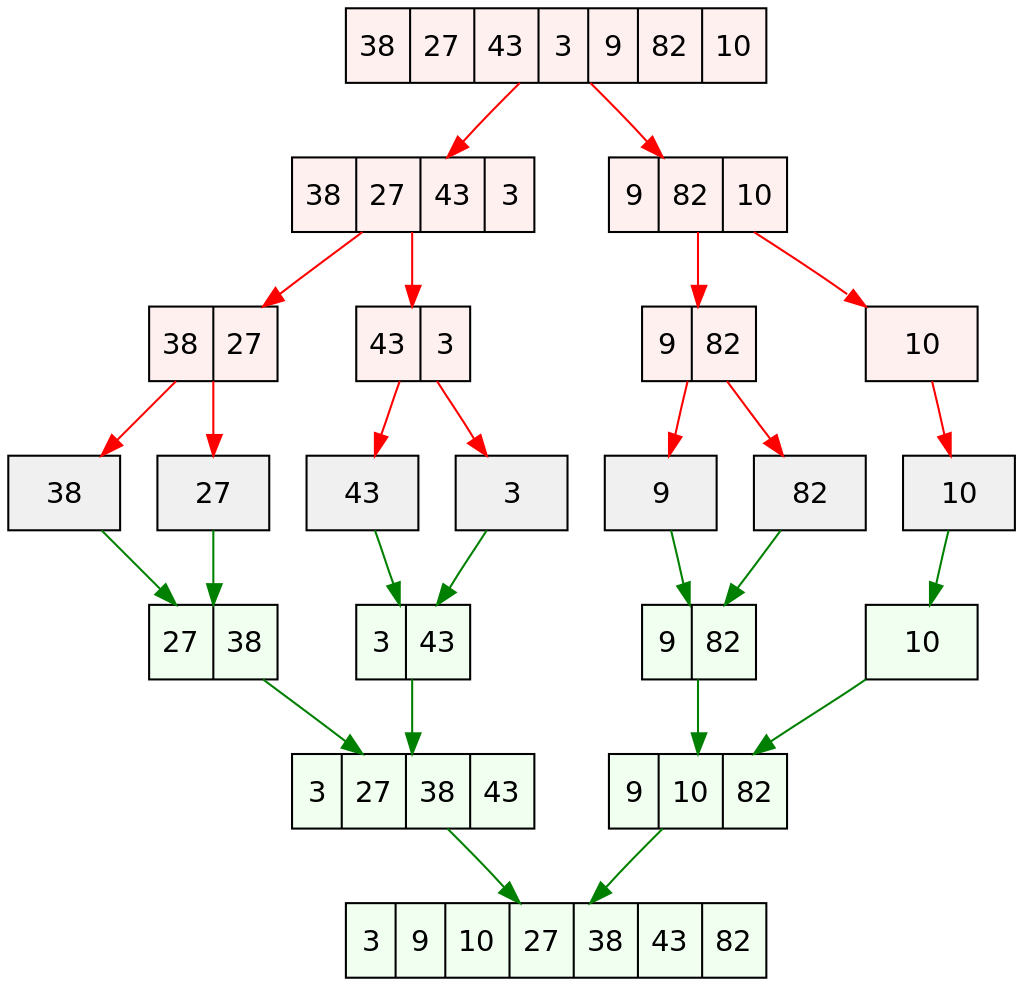
How to Merge

3

14

20

7

8

50

sorted: 

Set a mark on the two arrays to be merged

3

7

8

14

20

50

Time Complexity

  • Divide the array by two every time，divide at most \(\log n\) times (just like binary search)
  • Every layer we use \(O(n)\) time to merge back
  • total of \(O(n\log n)\)
  • mathematical proof：master theorem

In other D&C algorithms, if the merge complexity is \(f(x)\), then the whole complexity would be \(O(f(x)\times \log n\))

最大連續元素和

Given a sequence, what is the maximum continuous sum(can start and end in any place)

ex: 1 2 -3 4 5，answer：4+5=9

divide the sequence in half, the max continuous sum can either be in the left part or the right part, or it could be go across the two halfs.

We calculate the left and right by recursion.

For continuous sum that go across the middle, we calculate the two max sums both starting from the middle, and ending anywhere at the left and right, then add the together.

Complexity: calculating sum across the middle takes \(O(n)\), so the total is \(O(n\log n)\)

例題

最近點對

王老先生

太陽軍團

大樓外牆廣告

abc 248 ex - beautiful subsequence

Dynamic Programming

Fibonocci

f(n) = f(n - 1) + f(n - 2)

f(4)

f(3)

f(2)

f(2)

f(1)

f(1)

f(0)

f(1)

f(0)

f(2) has been calculated multiple times
time complexity O(2^n)

Store the calculated answers

f[n] = f[n - 1] + f[n - 2]

f(0)

f(1)

f(3)

f(2)

f(4)

O(n)

Dynamic Programming

  • The answer can be evaluated using a subproblem
  • There's a starting point of the subproblems

Though Process

  1. Define the states(subproblems)
  2. Think how do we evaluate our bigger answer using its subproblems
  3. Verify your algorithm

Staircase

There's a staircase with N steps

Every time you can step 1 or 2 steps

How many combination of steps you can take to reach the Nth step?

ex:

N=1，can only take 1 step, answer = 1

N=2，take two 1 steps, take one 2 steps

N=3，1+1+1, 1+2, 2+1

What is the state?

dp[i] = the number of combinations to teach the i'th step

 

How do we calculate dp[i] from dp[0], dp[1]...dp[i - 1]

We can only reach the i'th step from i-1 and i-2

So if there is dp[i-1] ways to reach i-1 step, than it is also how much we can reach i.

and if there is dp[i-2] ways to reach i-2, than it is also how much we can reach i

 

So the formula is \(dp[i] = dp[i-1] + dp[i-2]\)

Conclusion

set starting point dp[1] = 1、dp[2] = 2

transition formula dp[i] = dp[i - 1] + dp[i - 2]

O(n)

Salary

A performer has N working days.

Every day there is exactly 1 performance invitation with different pay across everyday.

However he can not work for 2 consecutive days.

What is the largest payment the performer can get?

ex:

n=5

payments of the N days 1, 2, 3, 1, 5

choose day 1, 3, 5 will get you a salary of 9, which is the largest

  • dp[i] = most money if we choose days to work from the first to i'th day
  • How do we calculate dp[i] from dp[0], dp[1]...dp[i - 1]?

For the i'th day, there's two possible outcomes

  1. work that day, then you can only work from day 1 to i-2
  2. don't work，then you can choose days to work from day 1 to i-1

Then we realize that choose days to work from day 1 to i-2 = dp[i-2]

 

work from day 1 to i-2 = dp[i-1]

\(dp[i] = max(dp[i-1], dp[i-2]+pay[i])\)

dp[1] = pay[i]

dp[2] = max(pay[1], pay[2])

 

O(n)

女裝

在總共n天的暑訓中

每天會從林O閎、何O甫、林O銓3人中選1人女裝

這3人在第i天女裝的美麗值分別為a[i], b[i], c[i]

但他們都不願意連續兩天女裝

請問最多的美麗值總合為多少?

ex:

n = 4

a = 1, 3, 4, 2,、b = 2, 4, 1, 5、c = 3, 1, 2, 6

第1天林O銓，第2天何O甫，第三天林O閎，第四天林O銓

能獲得最多美麗值為17

題目純屬虛構，如有雷同純屬巧合

女裝

在總共n天的暑訓中

每天會從林O閎、何O甫、林O銓3人中選1人女裝

這3人在第i天女裝的美麗值分別為a[i], b[i], c[i]

但他們都不願意連續兩天女裝

請問最多的美麗值總合為多少?

如何定義問題?

定義d[i]為0~i天最多的美麗值

那麼轉移式是d[i] = d[i - 1] + max(a[i], b[i], c[i])?

題目要求不能連續2天同1人女裝

這樣的轉移式是錯的

改變一下定義

定義d[i][j]為0~i天能獲得的最大美麗值

且第i天選擇了第j個人女裝

總共3個人，j有0, 1, 2三種狀況

假設第i天選了第0個人

第i - 1天只能選第1或2人

轉移式為

  1. d[i][0] = max(d[i - 1][1], d[i - 1][2]) + a[i]
  2. d[i][1] = max(d[i - 1][0], d[i - 1][2]) + b[i]
  3. d[i][2] = max(d[i - 1][0], d[i - 1][1]) + c[i]

結論

邊界為d[0][0] = a[0]、d[0][1] = b[0]、d[0][2] = c[0]

轉移式有三條

  • d[i][0] = max(d[i - 1][1], d[i - 1][2]) + a[i]
  • d[i][1] = max(d[i - 1][0], d[i - 1][2]) + b[i]
  • d[i][2] = max(d[i - 1][0], d[i - 1][1]) + c[i]

時間複雜度為O(n)

例題

最大連續子序列

最長遞增子序列

背包問題

atcoder dp contest (dp題單，從基礎到很難都有)

Greedy

Make the best move every step

aka. Dynamic Programming with only one subproblem every time

There's N lines [Li, Ri] on a 1d plane, select the most amount of lines that doesn't overlap with each other.

Overlapping lines

Observation: when we consider lines from left two right, if we come across two lines that overlaps, choose the left one is always optimal

Proof：if we choose the right one then there is less space to fit more lines in the right side.

Algorithm：Sort the lines with there right bounds, then consider lines from left to right, is we see a line overlaps with the previous one, we abandon it.

例題

誰先晚餐

物品堆疊

蘿莉切割問題(霍夫曼編碼)

昨天晚上，一等一被殺了

STL函式庫

標準樣板函式庫

c++內建函式庫，集結非常多好用資料結構和演算法實作

只要#include <bits/stdc++.h> 就會引入所有STL工具

函式設計為可以互相混用，讓運用非常有彈性，宣告方法也大致類似

常用STL函式

vector

動態陣列(= c的malloc，可以隨時擴展陣列容量) 的實作，並可配合許多其他STL函式操作

 

宣告：vector<TYPE> NAME(SIZE, INIT);

尾端新增：NAME.push_back(VALUE);

隨機存取：NAME[INDEX]

大小：NAME.size()

sort

O(nlogn)排序

 

小到大：

sort(起點，終點);

 

大到小：

sort(起點，終點，greater<TYPE>());

如果用vector：起點=NAME.begin()，終點=NAME.end()

一般陣列：起點=NAME，終點=NAME+長度

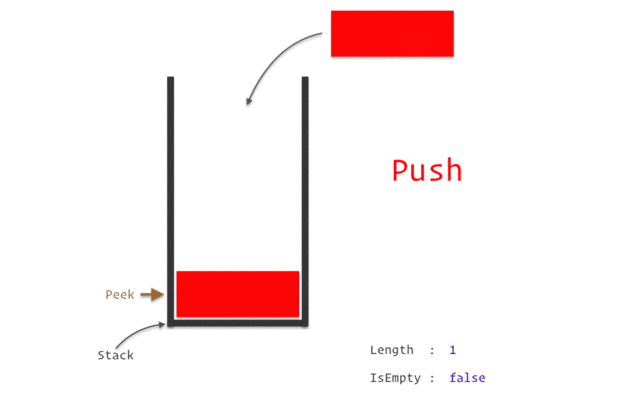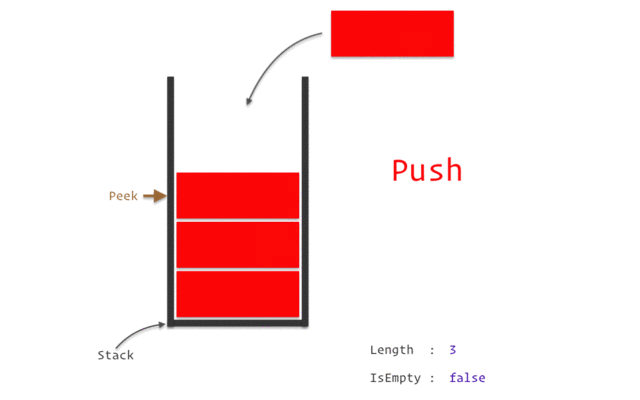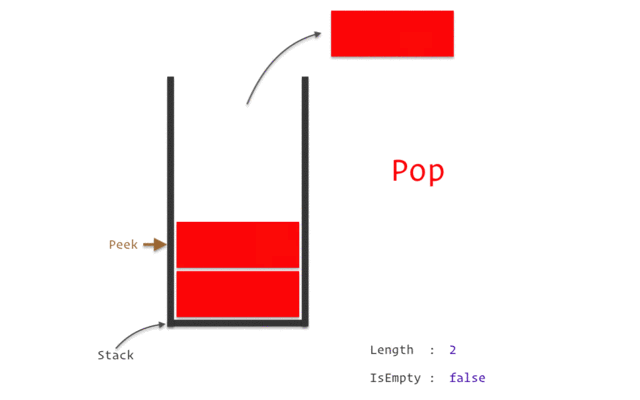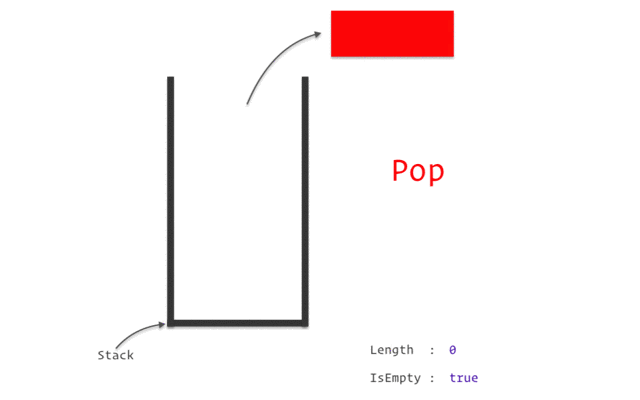
stack

stack資料結構實作

stack性質：先進後出(如圖)

 

宣告：stack<TYPE> NAME;

新增：NAME.push(VALUE);

刪除：NAME.pop();

頂端直：NAME.top()

大小：NAME.size()

基本上用vector是一樣的事

queue

像排隊一樣

先進先出

 

宣告：queue<TYPE> NAME;

新增：NAME.push(VALUE);

刪除：NAME.pop();

前端值：NAME.front()

尾端值：NAME.back()

大小：NAME.size()

priority_queue

優先度最高的會在頂端，heap實作

刪除，新增：O(log n)

取值：O(1)

 

宣告：priority_queue<TYPE> NAME;(值最大在頂端)

            priority_queue<TYPE,vector<int>,greater<int>> NAME(最小)

新增：NAME.push(VALUE);

刪除：NAME.pop();

頂端值：NAME.top()

大小：NAME.size()

set

自動排序且不重複的集合，紅黑樹(平衡二元樹)實作
複雜度皆為log n

 

宣告：set<TYPE>NAME;

新增：NAME.insert(VALUE);

刪除：NAME.erase(VALUE);

找第一個大於等於：NAME.lower_bound(VALUE)

大小：NAME.size()

map

由一個關鍵字和對應的值組成

複雜度皆為log n

 

宣告：map<TYPE,TYPE>NAME;

新增：NAME.insert({VALUE,VALUE});

刪除：NAME.erase(VALUE);

找第一個大於等於：NAME.lower_bound(VALUE)

大小：NAME.size()

lower_bound / upper_bound

對陣列二分搜的實作

lower_bound：找出陣列中"大於或等於"val的最小值的位置

auto it = lower_bound(v.begin(), v.end(), val);

 

upper_bound：找出vector中"大於"val的最小值的位置：

auto it = upper_bound(v.begin(), v.end(), val);

  • 2021建中資讀
  • ap325

參考資料

Copy of 算法

By alan lai

Made with Slides.com

Copy of 算法

  • 81

More from alan lai