線段樹
優化序列的區間詢問
給一序列,支援求區間和,和修改每一個元素的值
暴力:修改\(O(1)\),查詢\(O(n)\)
前綴和:修改\(O(n)\),查詢\(O(1)\)
線段樹:修改\(O(\log n)\),查詢\(O(\log n)\)
把區間一直分一半 (二元樹)
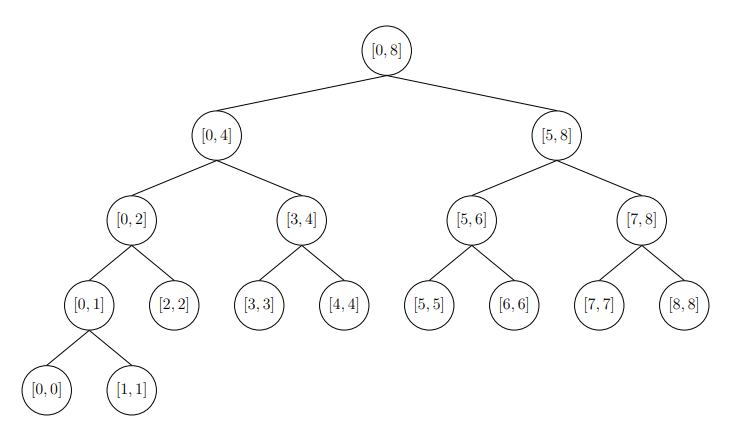
總共log n層
每一個節點存那個區間的答案
假設想查詢3~8的和

圈起來的節點答案加起來
aka從根結點遞迴把包含到的區間加起來

詢問3~8
[3,8]不貼合[0,8]
[3,8]有覆蓋到[0,4],遞迴到那

詢問3~4 (查詢區間不能超過目前節點)
[3,4]不貼合[0,4]
[3,4]沒有覆蓋到[0,2],但[4,4]有,遞迴到那

詢問3~4
[3,4]貼合[3,4],回傳此節點答案

詢問3~4

詢問3~8
[3,8]不貼合[0,8]
[3,8]有覆蓋到[5,8],遞迴到那

詢問5~8
[5,8]貼合[5,8]
回傳此節點答案

詢問5~8
[5,8]貼合[5,8]
回傳此節點答案
詢問複雜度\(O(\log n)\)
最多log n層,而且遞迴兩個分枝的次數不會太多
單點修改
如要更新位置i,只需一路遞迴到[i,i]的節點,並且往上一路更新
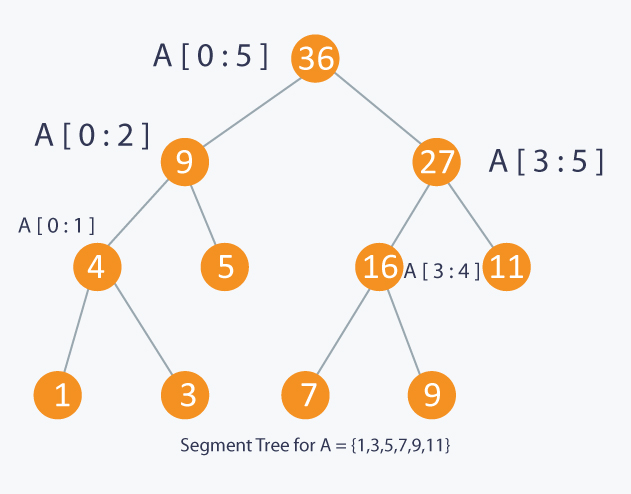
更新3成2

更新3成2

更新3成2

更新3成2
2

更新3成2
2
11

更新3成2
2
11
22

更新3成2
2
11
22
31
#include <bits/stdc++.h>
using namespace std;
int tree[400010], val[100010];
void build(int v, int l, int r){
if(l==r){
tree[v]=val[l];
return;
}
int mid=(l+r)>>1;
build(2*v, l, mid);
build(2*v+1, mid+1, r);
tree[v]=tree[2*v]+tree[2*v+1];
}
void upd(int v, int l, int r, int pos, int x){
if(l==r){
tree[v]=x;
return;
}
int mid=(l+r)>>1;
if(pos<=mid) upd(2*v, l, mid, pos, x);
else upd(2*v+1, mid+1, r, pos, x);
tree[v]=tree[2*v]+tree[2*v+1];
}
int qry(int v, int l, int r, int ql, int qr){
if(l==ql && r==qr) return tree[v];
int mid=(l+r)>>1;
if(qr<=mid) return qry(2*v, l, mid, ql, qr);
else if(ql>mid) return qry(2*v+1, mid+1, r, ql, qr);
else return qry(2*v, l, mid, ql, mid)+qry(2*v+1, mid+1, r, mid+1, qr);
}實作細節
- 陣列要開4*n
- 根節點編號1
- 如果目前節點是v,左節點是2*v,右是2*v+1
例題
區間最大連續和
線段樹節點存三個資訊:
- lmx=從左邊開始最大連續和
- rmx=從右邊開始最大連續和
- mx=介在中間的最大連續和
節點合併:
- mx=max(左mx,右mx, 左rmx+右lmx)
- lmx=max(左lmx, 左區間和+右lmx)
- rmx=max(rmx, 左rmx+右區間和)
#include <bits/stdc++.h>
using namespace std;
struct nd{
ll lmx, rmx, mx, sum;
};
ll val[200010];
nd tree[800010];
nd pull(nd &a, nd &b){
nd tmp;
tmp.mx=max(a.mx, b.mx);
tmp.mx=max(tmp.mx, a.rmx+b.lmx);
tmp.lmx=max(a.lmx, a.sum+b.lmx);
tmp.rmx=max(b.rmx, b.sum+a.rmx);
return tmp;
}
void build(int v, int l, int r){
if(l==r){
ll tmp=max(0, val[l]);
tree[v]={tmp, tmp, tmp, val[l]};
return;
}
int mid=(l+r)>>1;
build(2*v, l, mid);
build(2*v+1, mid+1, r);
tree[v]=pull(tree[2*v], tree[2*v+1]);
}
void upd(int v, int l, int r, int pos, ll x){
if(l==r){
ll tmp=max(0, x);
tree[v]={tmp, tmp, tmp, x};
return;
}
int mid=(l+r)>>1;
if(pos<=mid) upd(2*v, l, mid, pos, x);
else upd(2*v+1, mid+1, r, pos, x);
tree[v]=pull(tree[2*v], tree[2*v+1]);
}
nd qry(int v, int l, int r, int ql, int qr){
if(l==qr && r==qr) return tree[v];
int mid=(l+r)>>1;
if(qr<=mid) return qry(2*v, l, mid, ql, qr);
else if(ql>mid) return qry(2*v+1, mid+1, r, ql, qr);
return pull(qry(2*v, l, mid, ql, mid), qry(2*v+1, mid+1, r, mid+1, qr));
}
懶標
給一序列,支援求區間和,和對一個區間的數字都加上一個值
還記得差分?
\(O(1)\)修改
\(O(n)\)查詢
懶標(lazy tag) - 在一個節點標記那個區間都要被加上某個值
加值時如果加值區間和節點區間一樣,就在那裡打懶標(標記區間+某值)
之後如果遞迴時需要遞迴到更深處,就要把懶標的資訊推到左右子樹

0
0
0
0
0
0
0
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
0
0
0
0
0
0
0
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
0
0
0
0
0
14
0
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
0
0
0
0
0
14
14
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
0
0
0
0
0
14
14
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
0
0
0
0
0
14
14
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
0
0
0
14
0
14
14
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
0
14
0
14
0
14
14
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
28
14
0
14
0
14
14
0
0
0
將3~6加7
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
複雜度\(O(\log n)\)
跟區間查詢一樣
28
14
0
14
0
14
14
0
0
0
查詢3~6的和
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
28
14
0
14
0
14
14
0
0
0
查詢3~6的和
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
28
14
0
14
0
14
14
0
0
0
查詢3~6的和
0
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
28
14
0
14
7
14
14
0
0
0
查詢3~6的和
7
0
0
0
0
1 2 3 4 5 6 7 8
tag=7
tag=7
tag=7
\(O(\log n)\)
#include <bits/stdc++.h>
#define EB emplace_back
#define vci vector<int>
#define PII pair<int,int>
#define F first
#define S second
#define rep(X, a,b) for(int X=a;X<b;++X)
#define ALL(a) (a).begin(), (a).end()
#define SZ(a) (int)(a).size()
#define NL "\n"
#define LL long long
using namespace std;
LL tree[5*500000], num[500010], tag[5*500000]={0};
void push(int v, int l, int r){
int mid=(l+r)>>1;
tag[2*v]+=tag[v];
tag[2*v+1]+=tag[v];
tree[2*v]+=(mid-l+1)*tag[v];
tree[2*v+1]+=(r-mid)*tag[v];
tag[v]=0;
}
void build(int v, int l, int r){
if(l==r) tree[v]=num[l];
else{
int mid=(l+r)>>1;
build(2*v, l, mid);
build(2*v+1, mid+1, r);
tree[v]=tree[2*v]+tree[2*v+1];
}
}
void modify(int v, int l, int r, int ul, int ur, LL x){
if(l==ul && r==ur){
tag[v]+=x;
tree[v]+=(r-l+1)*x;
return;
}
if(tag[v]) push(v, l, r);
int mid=(l+r)>>1;
if(ur<=mid) modify(2*v, l, mid, ul, ur, x);
else if(ul>mid) modify(2*v+1, mid+1, r, ul, ur, x);
else{
modify(2*v, l, mid, ul, mid, x);
modify(2*v+1, mid+1, r, mid+1, ur, x);
}
tree[v]=tree[2*v]+tree[2*v+1];
}
LL query(int v, int l, int r, int ql, int qr){
if(l==ql && r==qr) return tree[v];
if(tag[v]) push(v, l, r);
int mid=(l+r)>>1;
if(qr<=mid) return query(2*v, l, mid, ql, qr);
else if(ql>mid) return query(2*v+1, mid+1, r, ql, qr);
return query(2*v, l, mid, ql, mid)+query(2*v+1, mid+1, r, mid+1, qr);
}
持久化線段樹
時間線段樹
線段樹
By alan lai
線段樹
- 195



