字串演算法
hash
雜湊
hash function
字串轉換成數字
fast
hash
function
48763
用途
\(O(1)\)判斷兩字串是否相同
隱憂:hash須注意碰撞(不同子串輸出相同數字)
因為字串有無限多種,沒辦法在變數範圍對應到所有可能
Rolling Hash
將字串視為多項式
\( (s_0\times p^{n-1}+s_1\times p^{n-2}+...+s_{n-2}\times p^1+s_{n-1}\times p^0) \mod m \)
字串為\(s\)
p是一個夠大的質數(可以=29, 257)
m為很大的質數(通常=\(10^9+7\))
區間hash -> 前綴hash相減
建前綴hash:\(h(i)=(h(i-1)*p^1+s_i*p^0)\mod m\)
i~j區間hash:
\((h(j)-h(i-1)\times p^{j-i})\mod m\)
trie字典樹
用途:有效率的查詢一個字是不是在一堆字裡面
建樹:如果一些字前綴都一樣,則一樣的部分合再一起
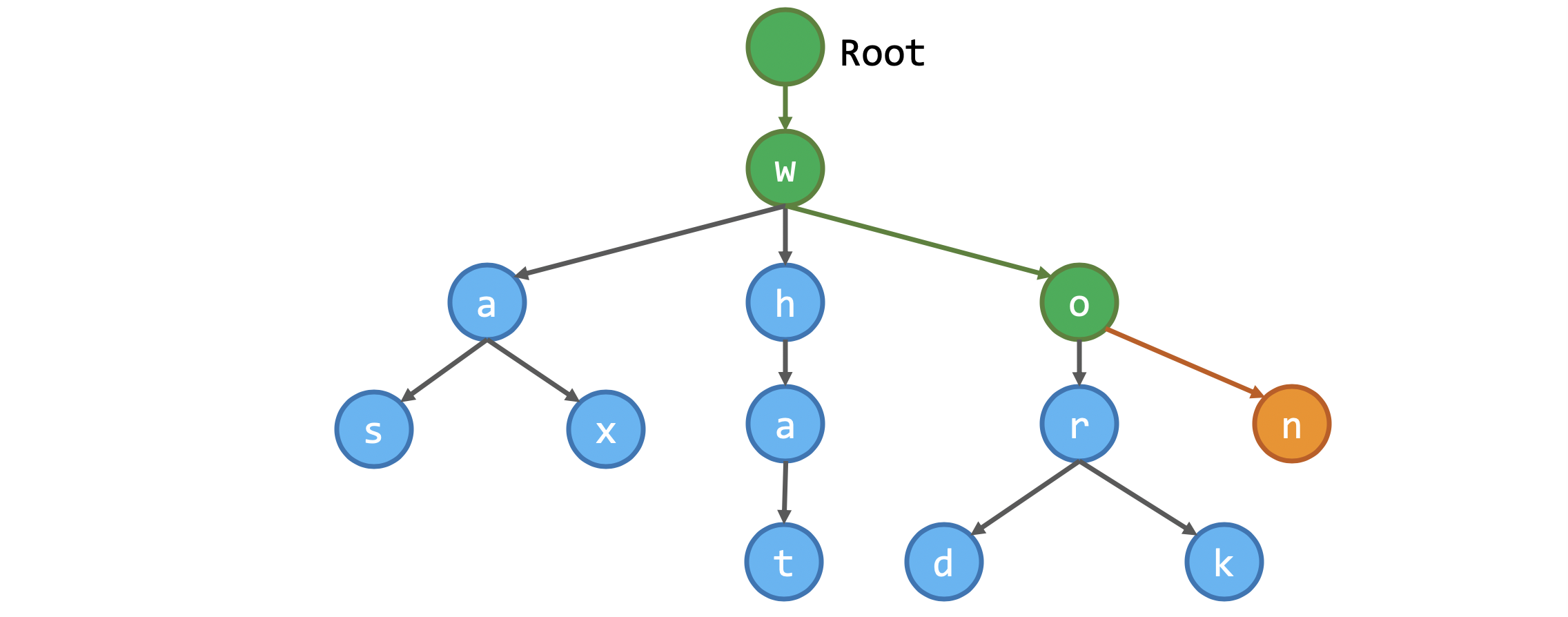
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
i
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
i
l
建樹:如果一些字前綴都一樣,則一樣的部分合再一起

加入while
i
l
e
z-algorithm
\(O(n)\)確定性字串匹配 (不會碰撞)
建一z陣列\(z[i]\),代表從\(s_i\)開始跟\(s\)的最長共同前綴
(z[0]為未定義)
a a b c a a b
z[] - x 1 0 0 3 1 0如何運用在字串匹配?
ex:段落是\(p\),要匹配的是\(s\)
對\(s\$p\) (兩字串合併中間插入$) 建一個z陣列
當\(z[i]=|s|\)時即為匹配
p=baabaa, s=aab
a a b $ b a a b a a
z[] = x 1 0 0 0 3 1 0 2 1如何建z陣列?
首先維護\(l\), \(r\),代表面前以匹配最右的區間
對於當前位置\(i\),有兩個情況
- 若\(i>r\),直接暴力計算\(z[i]\),並更新\(l, r\)
- 若\(i\le r\),\(z[i] = min(z[i-l], r-i+1)\)作為初始值,之後暴力擴展\(z[i]\)
l=4, r=6, i=5
a a b c a a b
z[] - x 1 0 0 3l=5, r=7, i=6
a a a a b a a a c
z[] - x 3 2 1 0 3均攤\(O(n)\)
void match(vector<int> &z, string s){
int len=s.size();
z[0]=0;
int l=0, r=0;
rep(i,1,len){
if(i<=r) z[i]=min(z[i-l], r-i+1);
while(i+z[i]<len && s[z[i]] == s[i+z[i]]) z[i]++;
if(i+z[i]-1>r) l=i, r=i+z[i]-1;
}
}
kmp
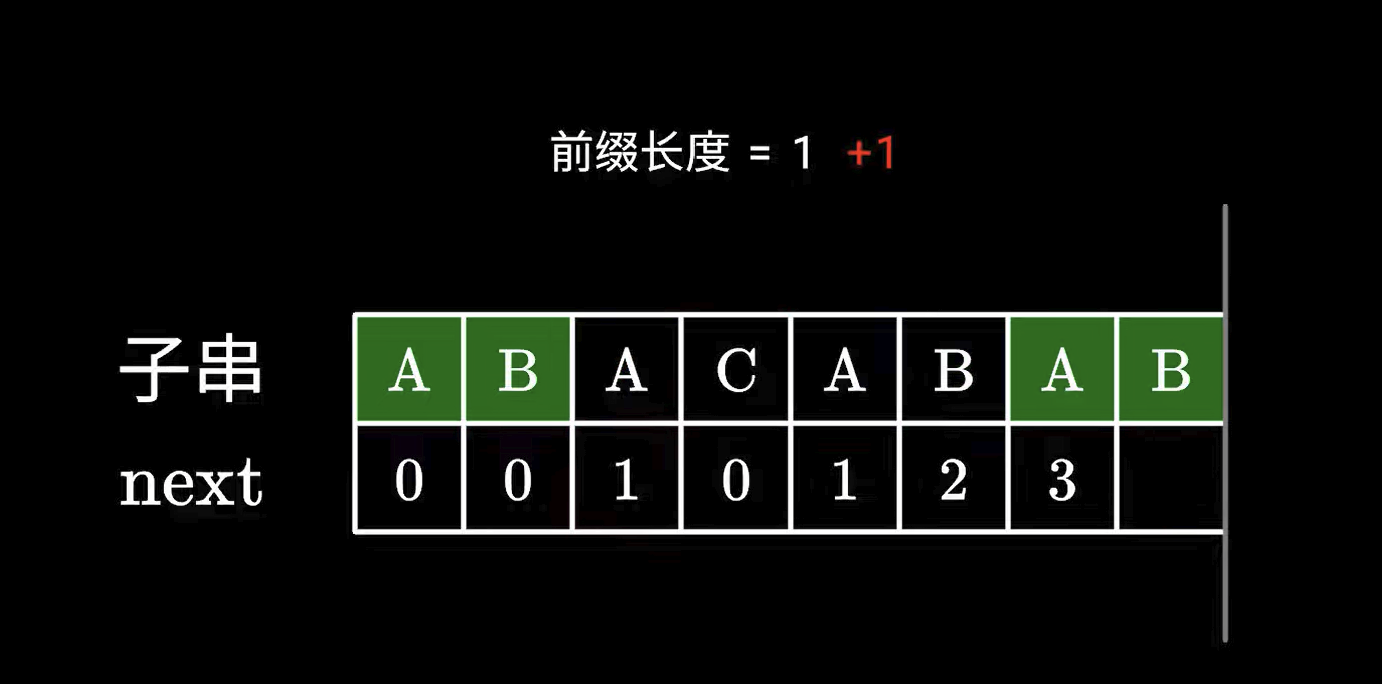
備註 7:32
if this two not the same, next=0
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int f[1000010]={0};
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
string a, b;
cin>>a>>b;
int lena=a.size(), lenb=b.size();
// build failure function
f[0]=-1;
int j=-1;
for(int i=1;i<lenb;++i){
while(j!=-1 && b[j+1]!=b[i]) j=f[j];
if(b[j+1]==b[i]) j++;
f[i]=j;
}
//match
int ans=0;
j=-1;
for(int i=0;i<lena;++i){
while(j!=-1 && a[i]!=b[j+1]) j=f[j];
if(a[i]==b[j+1]) j++;
if(j==lenb-1) ans++, j=f[j];
}
cout<<ans<<"\n";
}
0-based,無法匹配 = -1
字串演算法
By alan lai
字串演算法
- 191



