序列上相關的演算法
- 前綴和
- 差分
- 單調隊列
- 掃描線
想到甚麼就講甚麼
一些題目
前綴和
有一長為n個陣列a,記另一個陣列把每個a的前綴(1到每個位置)的總和記起來
aka. 有一個前綴和pre,pre[i]= a[1]+...+a[i]
算法:pre[i]=pre[i-1]+a[i]
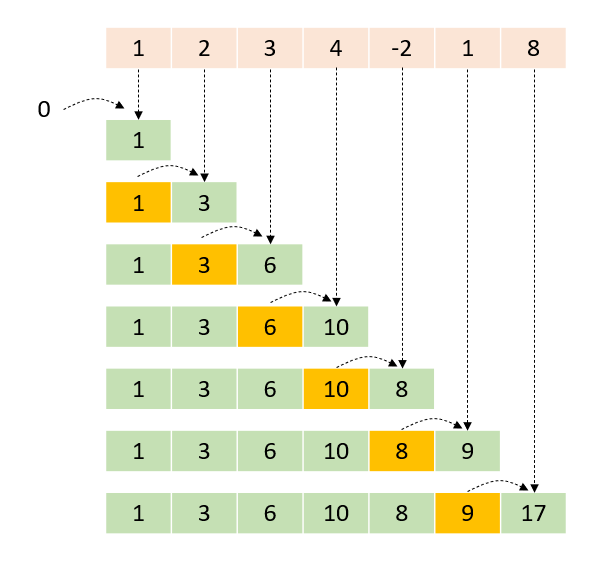
用途:區間和
若\(p_i\)=\(a_1+...+a_i\)
l~r的和:\(a_l+...+a_r=p_r-p_{l-1}\)
證:$$p_r=a_1+...+a_{l-1}+...+a_r$$
$$p_{l-1}=a_1+...+a_{l-1}$$
$$p_r-p_{l-1}=a_l+...+a_r$$
\(O(n)\)加值,\(O(n)\)算前綴和,\(O(1)\)區間和
例題(太多了><)
atcoder dp contest Candies
差分
對於差分陣列\(d_i=a_i-a_{i-1}\)
\(d_1=a_1\)
性質:差分陣列的前綴和即為原陣列
\(a_i=d_1+...+d_i\)
證:\(a_{i-1}+(a_i-a_{i-1})=a_i\)
用途:多筆區間修改後區間查詢
如果要在\(a_l...a_r\)都加\(x\)
先在\(d_l\)加\(x\),此時\(a_l...a_n\)都會被加\(x\),因為\(d_l\)到\(d_n\)用前綴和恢復為原陣列後都會包含到\(d_l\)
接下來在\(d_{r+1}\)減x,使的\(a_{r+1}...a_n\)都減回x
最後就只剩\(a_l...a_r\)加到x
\(O(1)\)加值,\(O(n)\)算前綴和,\(O(1)\)取值
缺點:加完每次都要\(O(n)\)前綴和,所以理想情形是當題目只需要一次加完之後再一次取值
例題
單調隊列
先看例題
用一個stack,維護一個遞減的序列
每加入一個數字x進stack,把最上面小於x的數字pop掉,直到大於x,這時最上面的數字就是最接近x且比x高的人
proof. 如果\(a_{i-1}<a_i\)那\(a_{i-1}\)一定不會是之後的高人,所以直接pop掉,之後都用不到
在pop的過程中,把某個\(a_i\) pop掉同時也pop掉所有在\(a_i\)前面且小於\(a_i\)的數,所以第一個pop不掉的數就是答案
複雜度:O(n)
proof:每個數字最多被操作到2次,第一次加到stack,第二次從stack pop掉,pop掉就不會再出現了
掃描線
將一個區間的左右接拆開,全部混再一起排序

電
orz
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 0
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 1
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 2
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 3
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 2
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 3
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 2
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 1
現在我們把每個區間的開頭結尾都拆開看成是數線上獨立的點
(不過要記是開頭還是結尾)
排序這2*n個點,從最左邊開始,遇到開頭就+1,結尾-1,每次走都取max
cnt: 0
#include <bits/stdc++.h>
using namespace std;
bool cmp(pair<int,int> a, pair<int,int> b){
return a.first<b.first;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
vector<pair<int,int>> save(n*2);
for(int i=0;i<n;++i){
cin >> save[i*2].first>> save[i*2+1].first;
save[i*2].second=1;
save[i*2+1].second=0;
}
sort(save.begin(), save.end(), cmp);
int cur=0, ans=0;
for(auto i:save){
if(i.second) ++cur;
else --cur;
ans=max(cur, ans);
}
cout << ans << "\n";
}掃描線
序列問題
By alan lai
序列問題
- 168



