Approximating Configuration Space with Few Convex Sets
Tobia Marcucci
Russ Tedrake
Peter Werner
Daniela Rus
Alexandre Amice
Motion Planning IS Hard Because Configuration Space is Complicated
Motion Planning IS Hard Because Configuration Space is Complicated
Describing Configuration Space As a Collection of Simple Sets makes motion planning tractable
Describing Configuration Space As a Collection of Simple Sets makes motion planning tractable
Automatically Decomposing Configuration Space
-
Computing Large Convex Regions of Obstacle-Free Space Through Semidefinite Programming (Deits et al. 2015)
-
Certified Polyhedral Decompositions of Collision-Free Configuration Space (Dai, Amice, et. al 2023)
-
Growing Convex Collision-Free Regions in Configuration Space using Nonlinear Programming (Petersen, et. al. 2023)
-
Approximating Robot Configuration Spaces with few Convex Sets using Clique Covers of Visibility Graphs (Werner, et. al. 2023)
Iterative Regional Inflation by Semidefinite programming (IRIS)
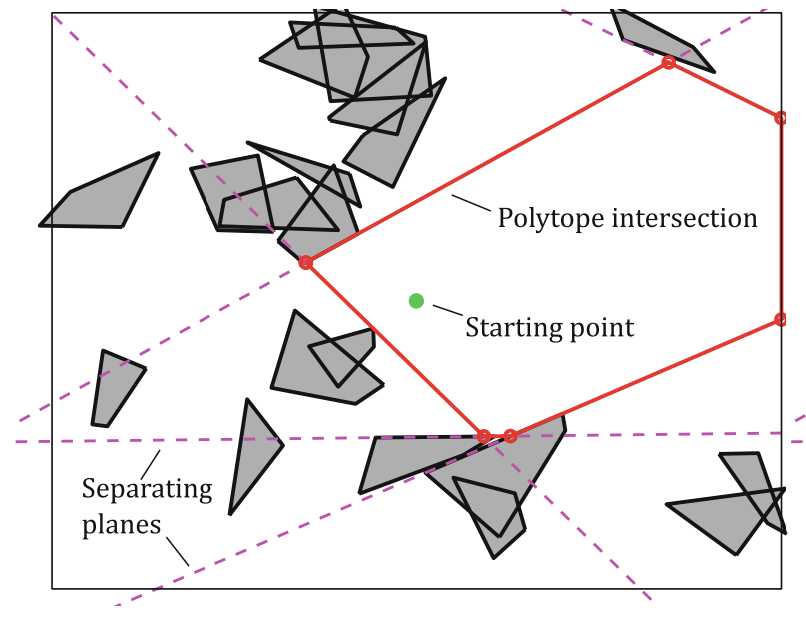
Credits: Robin Deits
Iterative Regional Inflation by Semidefinite programming (IRIS)
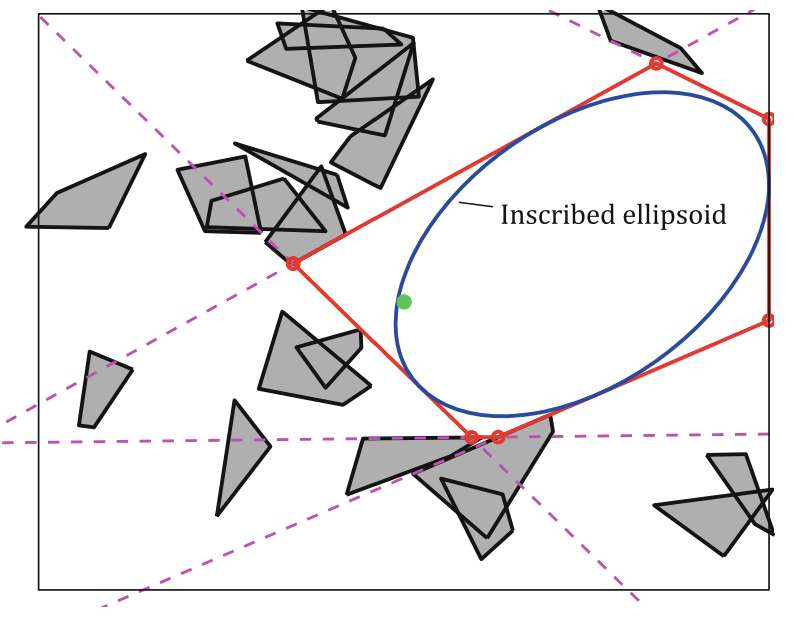
Credits: Robin Deits
Iterative Regional Inflation by Semidefinite programming (IRIS)
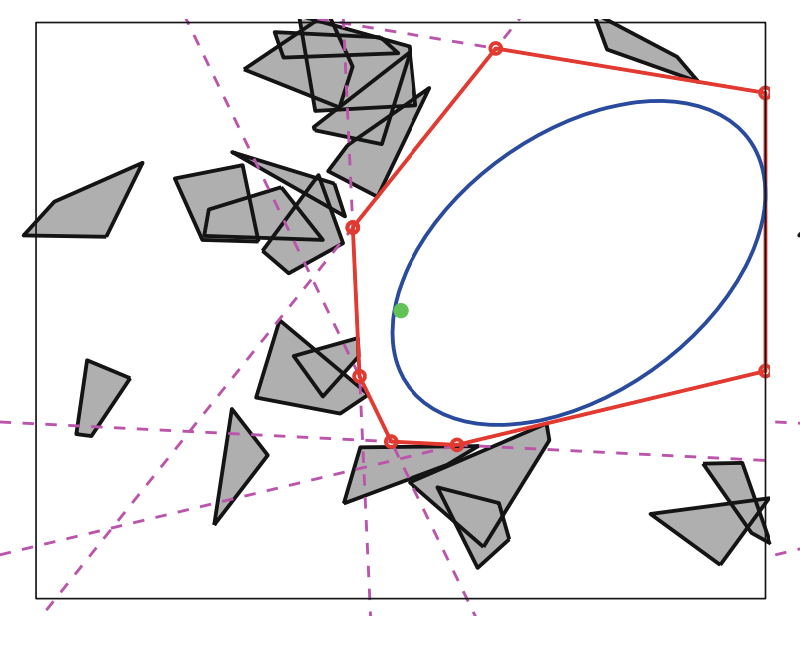
Credits: Robin Deits
Iterative Regional Inflation by Semidefinite programming (IRIS)
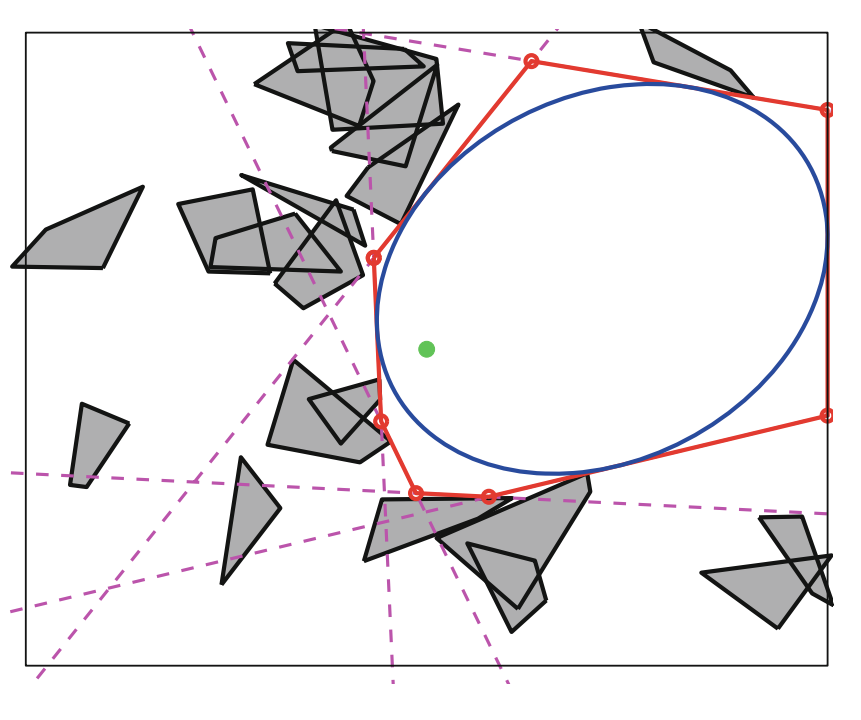
Credits: Robin Deits
Iterative Regional Inflation by Semidefinite programming (IRIS)
Credits: Robin Deits
Convex In Task Space Is Not Convex in Configuration Space
IRIS-NP
Configuration Space Generalizations
C-IRIS
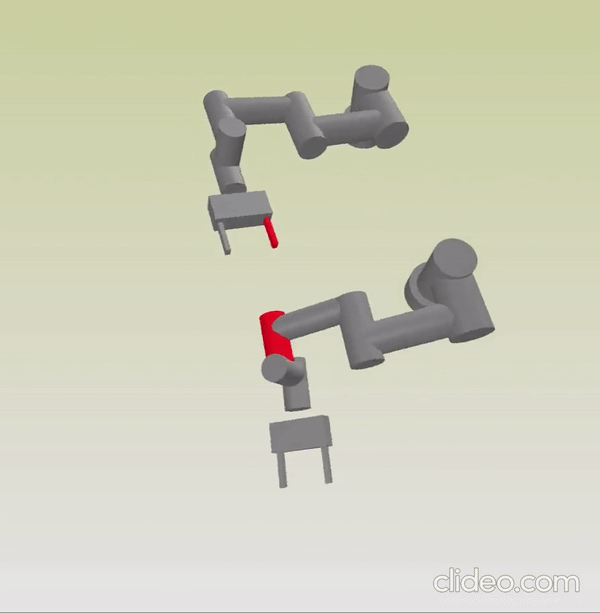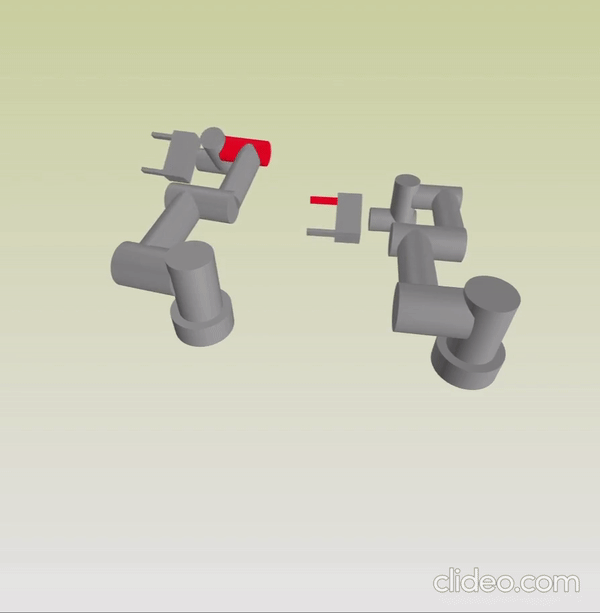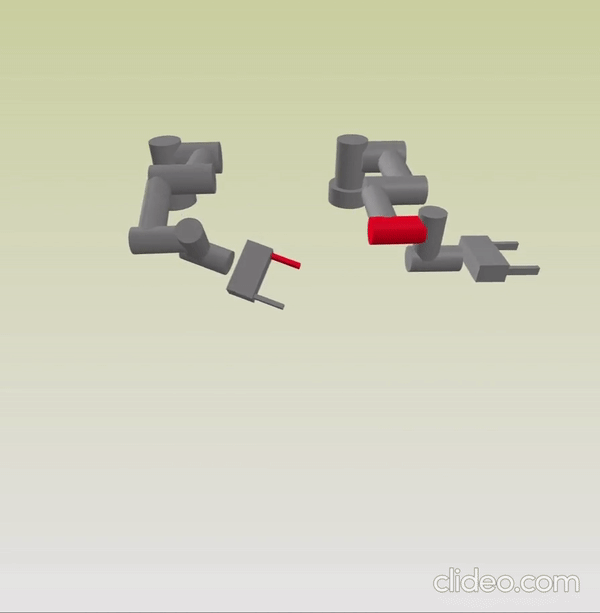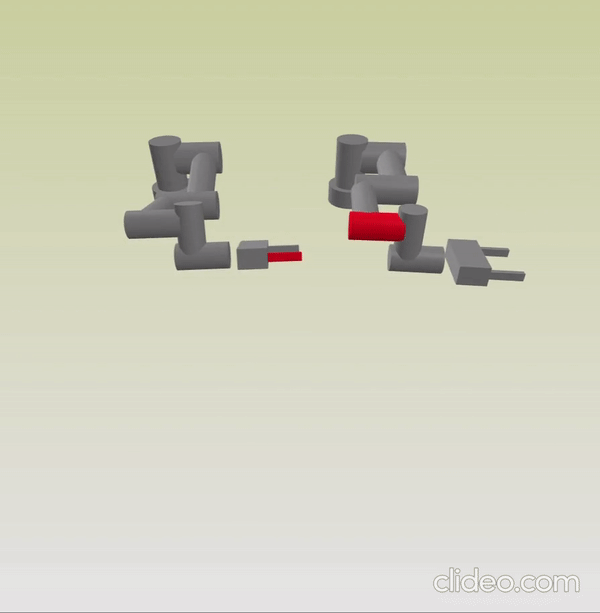
IRIS Steps
IRIS Steps
IRIS Steps
IRIS Features
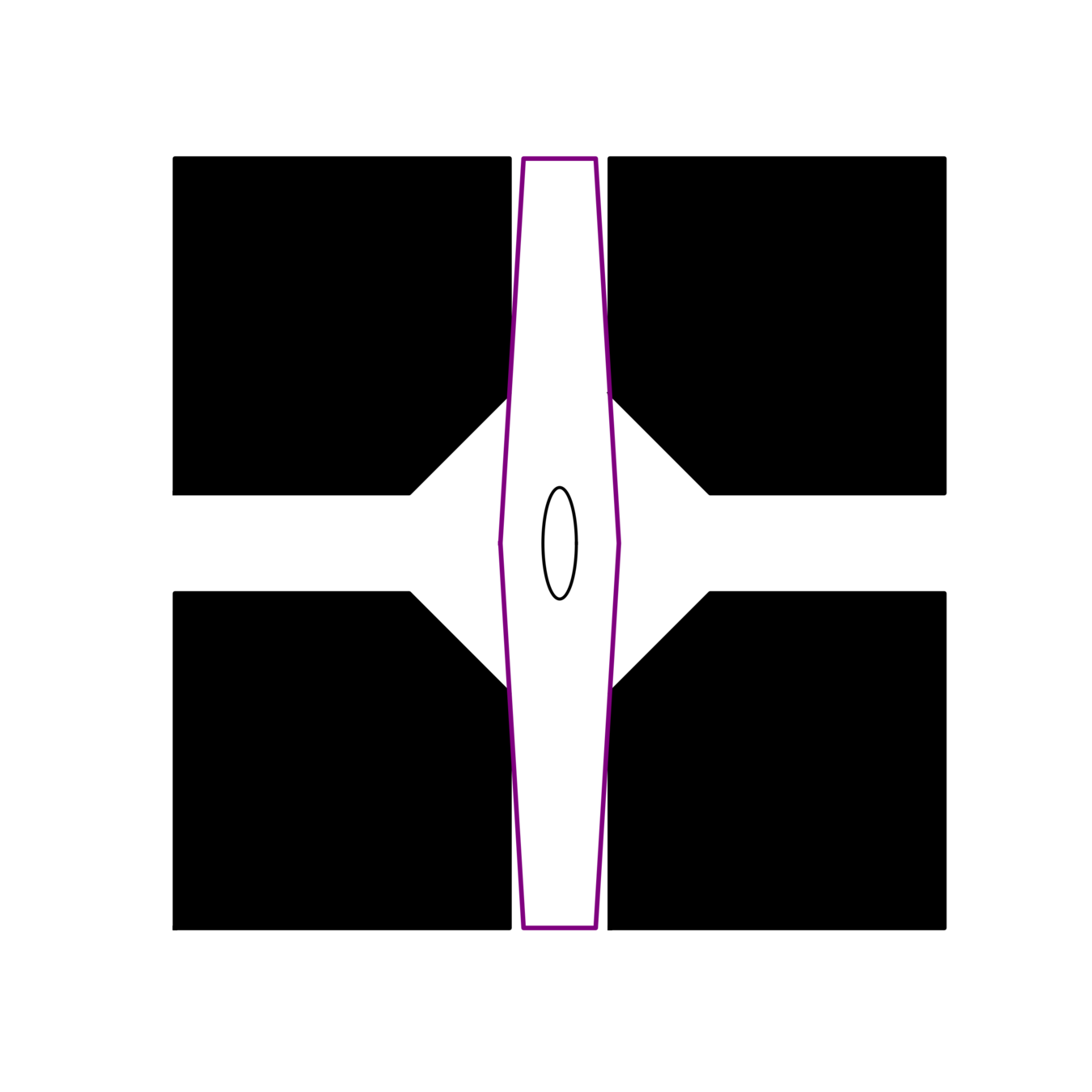
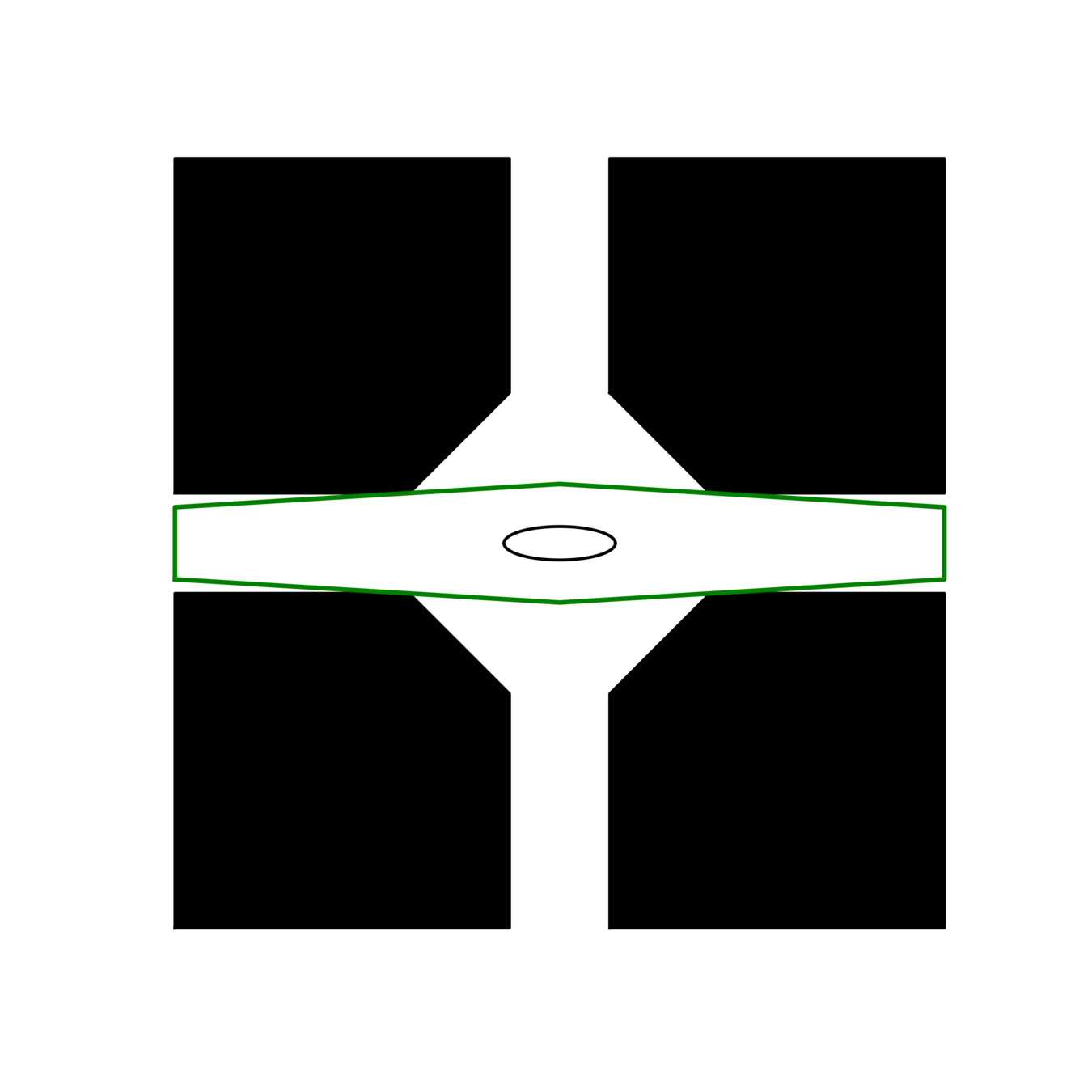
IRIS Features
Credit: Tommy Cohn
From a Single Region To A Cover
Problem Statement
How Hard Is This?
- Exact Cover of 2D polygon:
\exists \mathbb{R}-\text{complete}
- Approximate Cover:
As hard as checking if a system of polynomial equations has a root.
\text{APX}-\text{Hard}
No polynomial time algorithm can achieve an approximation ratio bounded by a constant factor.
There is an algorithm which achieves a logarithmic performance in the number of vertices with runtime
\mathcal{O}(n^{29} \log(n))
Naive Strategy
DownSides
Visibility Clique Cover Algorithm
Visibility Clique Cover
Visibility Clique Cover
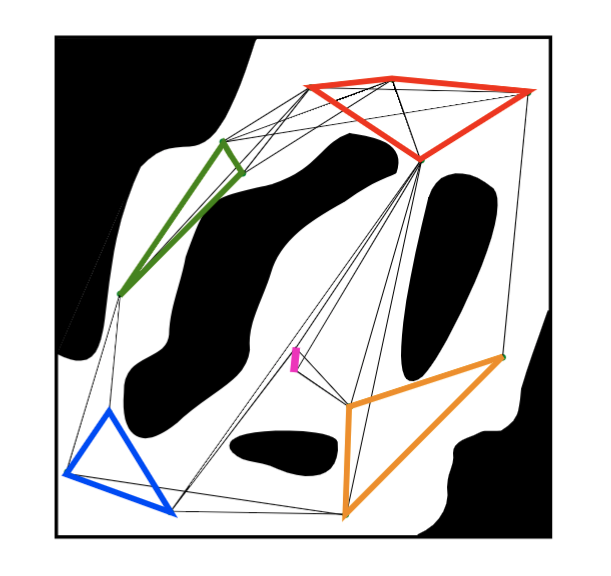
Visibility Clique Cover
Recall:
Visibility Clique Cover
Visibility Clique Cover
Visibility Clique Cover
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
\scriptsize{\mathcal{S} \text{ is convex iff } \forall a,b \in \mathcal{S} \Rightarrow \overline{ab} \subseteq \mathcal{S}}
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
\forall a,b \in \mathcal{S} \Rightarrow \overline{ab} \subseteq \mathcal{S}
a
b
\overline{ab}
a
b
\overline{ab}
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
\forall i,j \in \mathcal{K} \Rightarrow \{i,j\} \in \mathcal{E}
\mathcal{G} = (\mathcal{V}, \mathcal{E}),
Given a graph
\mathcal{G}
2
1
3
4
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
\forall i,j \in \mathcal{K} \Rightarrow \{i,j\} \in \mathcal{E}
2
1
3
4
2
1
3
4
2
1
3
4
\scriptsize{\mathcal{K_1} = \{2,3,4\}}
\scriptsize{\rightarrow \{1,3\} \notin \mathcal{E}}
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
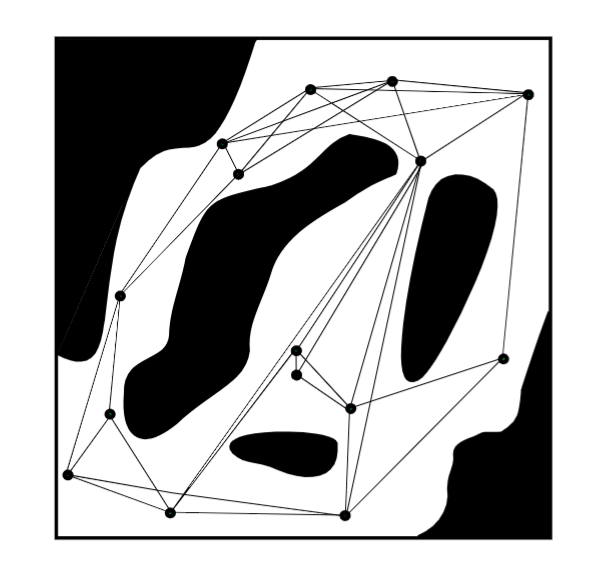
Visibility Graph
- Add edge if two points have line of sight
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
Visibility Graph
- Add edge if two points have line of sight
- Edges are collision-free line segments
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
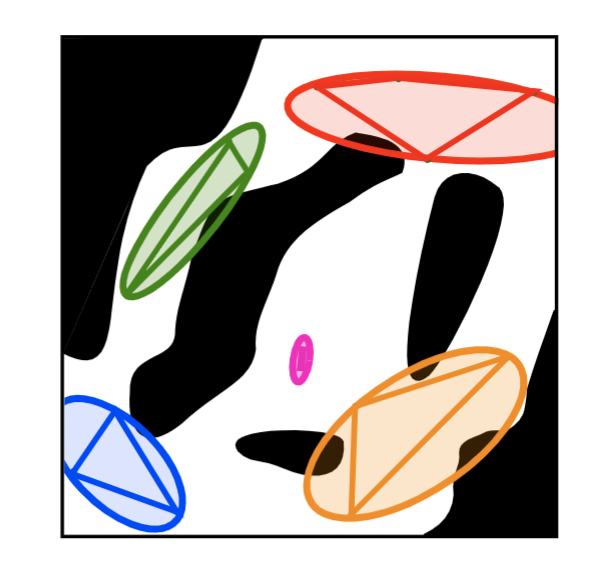
Collision-free convex sets
\scriptsize{a,b \in \mathcal{S} \Rightarrow \overline{ab} \subseteq \mathcal{S}\subseteq\mathcal{C}^\text{free}}
a
b
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
- Points inside a convex set form a clique on the visibility graph
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
- Points inside a convex set form a clique on the visibility graph
Cliques approximate convex sets
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
- Converse not true in general
\scriptsize{\mathcal{K} = \{1, 2, 3\} \text{ is a clique} }\\
\scriptsize{ \text{but }\textbf{conv}\{a_1, a_2, a_3\} \not \subseteq\mathcal{C}^\text{free} }
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
\scriptsize{\text{If } a_1,\dots, a_N \in \mathcal{S} \text{ then }}\\
\scriptsize{\mathcal{K} = \{1, \dots, N\} \text{ is a clique}}
Intuition
| Convex Set | Clique | Clique on V-Graph |
|---|
What is a ...
Proves to be a powerful heuristic!
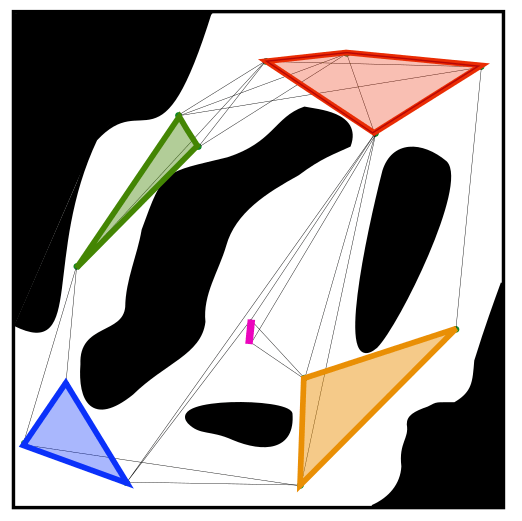
Cover continuous space in small number of continuous regions
Cover discrete graph in small number of cliques
Cover graph in small number of cliques
use approximations to minimum clique cover
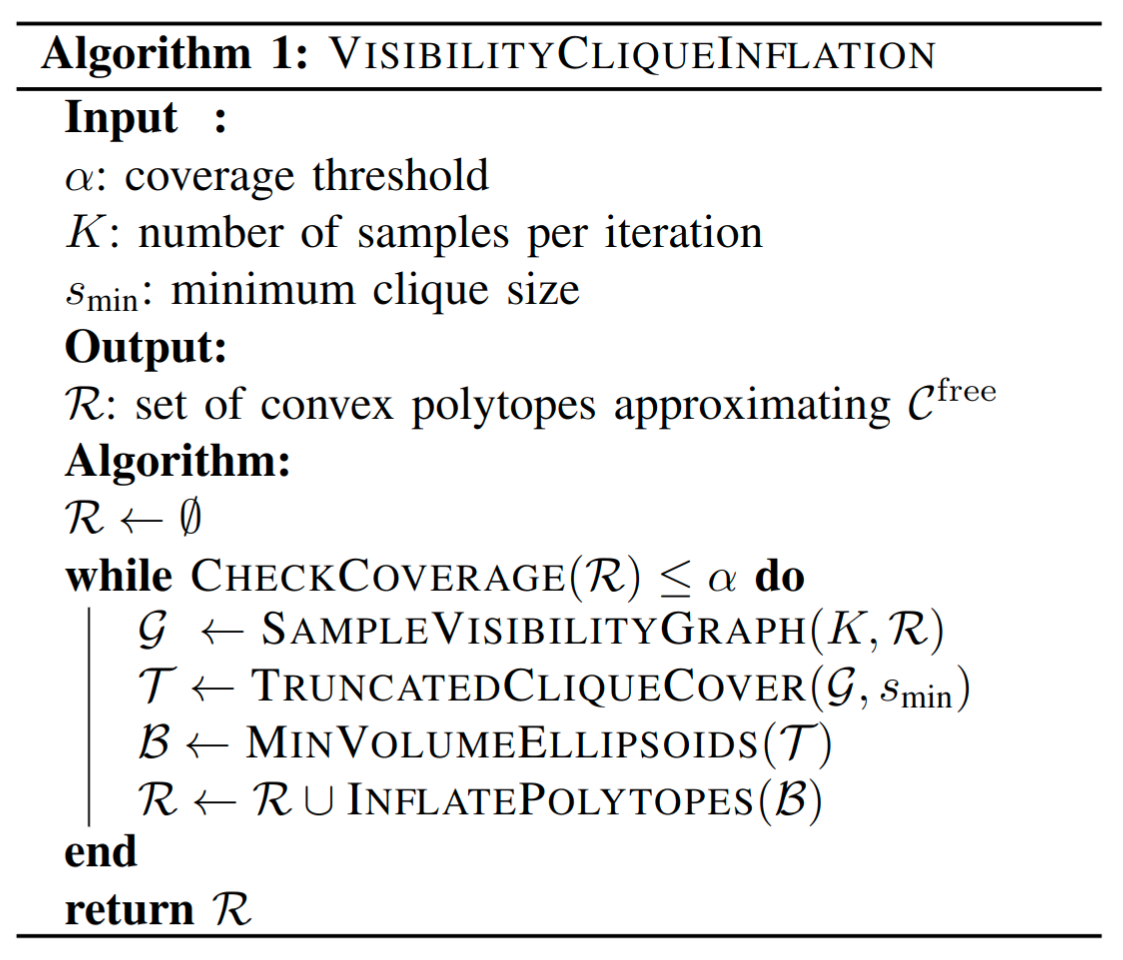
use repeated Max Clique solvesAdvantages
| Village | # of Regions | Time To Construct |
| Ours | 94 | 28 min |
| Naive | 198 | 45 min |
https://wernerpe.github.io/files/Village.html
| IIWA | # of Regions | Time To Construct |
| Ours | 46 | 95 min |
| Naive | 483 | 1483 min |
https://wernerpe.github.io/files/7DOF_IIWA_arxiv.html
Extension
The rest of this talk is work in progress
Are ClIques Convex Sets?
Not Even With Infinite Samples
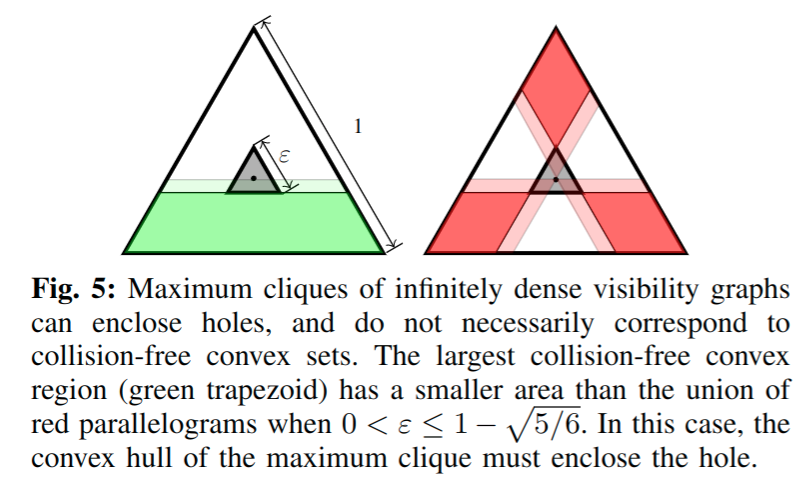
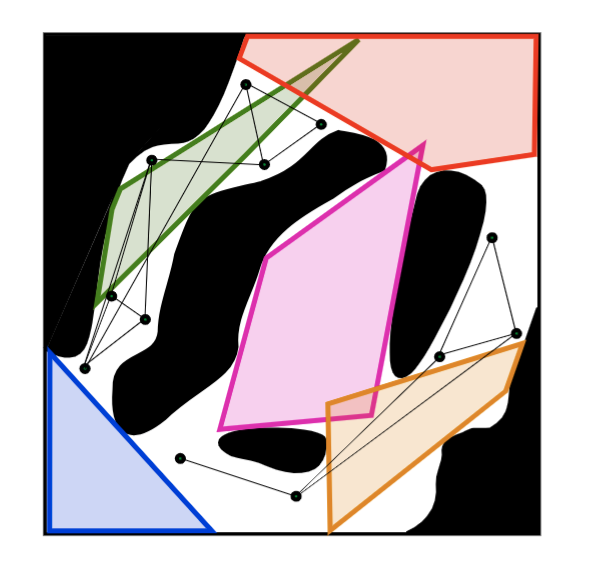
Greedy Clique Covering:
- compute largest clique
- remove it
- repeat
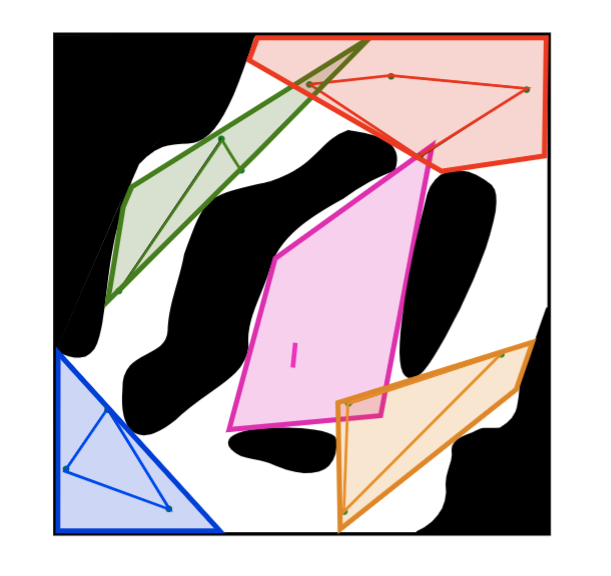
The minimum Clique Cover isn't The Minimum ConveX Cover
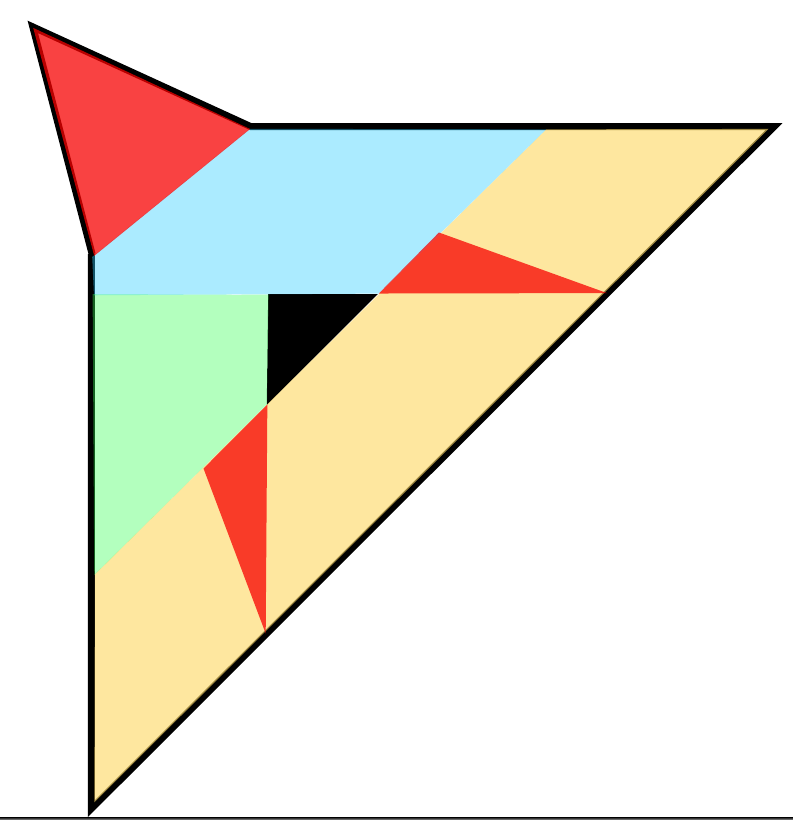
The minimum Clique Cover isn't The Minimum ConveX Cover
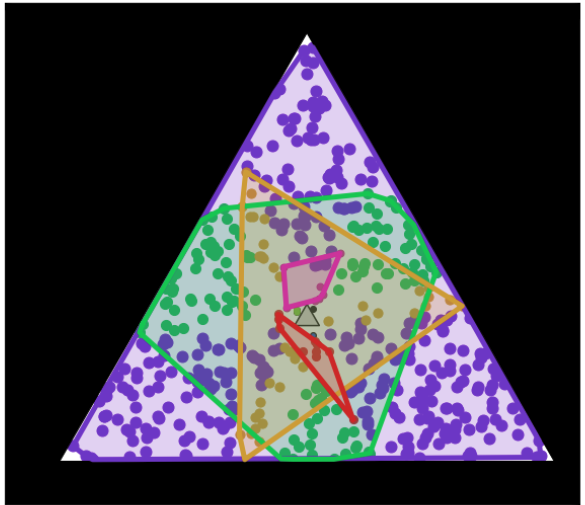
Obviously a problem
Solution
Ask for a clique cover that is more like a convex set
\max \sum_{i} x_{i} \textbf{ subject to }
\\
x_{i} + x_{j} \leq 1 \text{ if } (i,j) \notin \mathcal{E}
\\
x_{i} \in \{0,1\}
x_{i} \in \textbf{conv}\left(\mathcal{K}\right) \implies x_{i} \in \mathcal{K}
If the convex hull condition is violated, then your clique must contain a collision
Clique Cover MIP
\min \sum_{1 \leq i \leq M} c_{i} \textbf{ subject to }
\\
\sum_{i = 1}^{M} x_{v i} = 1 ~ \forall v \in \mathcal{V}
\\
x_{ui} + x_{vi} \leq c_{i} ~ \forall (u,v) \notin \mathcal{E}
\\
x_{vi}, c_{i} \in \{0,1\}
Max Clique Mip
\max \sum_{i} x_{i} \textbf{ subject to }
\\
x_{i} + x_{j} \leq 1 \text{ if } (i,j) \notin \mathcal{E}
\\
x_{i} \in \{0,1\}
Solution 1
\max_{x, c} \sum_{i} x_{i} \textbf{ subject to }
\\
x_{i} + x_{j} \leq 1 \text{ if } (i,j) \notin \mathcal{E}
\\
x_{i} \in \{0,1\}
c_{i}^{T}(q_{i} - q_{j}) \geq (1- x_{i}) - M_{ij}(1-x_{j})
If the th point is in the clique, but the th point is not, then find a separating plane between them.
i
j
Solution 2
\max_{x, E} \sum_{i} x_{i} \textbf{ subject to }
\\
x_{i} + x_{j} \leq 1 \text{ if } (i,j) \notin \mathcal{E}
\\
x_{i} \in \{0,1\}
\begin{bmatrix} q_{i} \\ 1 \end{bmatrix}^{T}
E
\begin{bmatrix} q_{i} \\ 1 \end{bmatrix}
\leq 1 + M_{i}(1-x_{i})
\begin{bmatrix} q_{i} \\ 1 \end{bmatrix}^{T}
E
\begin{bmatrix} q_{i} \\ 1 \end{bmatrix}
\geq (1-x_{i})
Find a classifier for the clique whose decision boundary is a convex set
Solution 2
Find a classifier for the clique whose decision boundary is a convex set
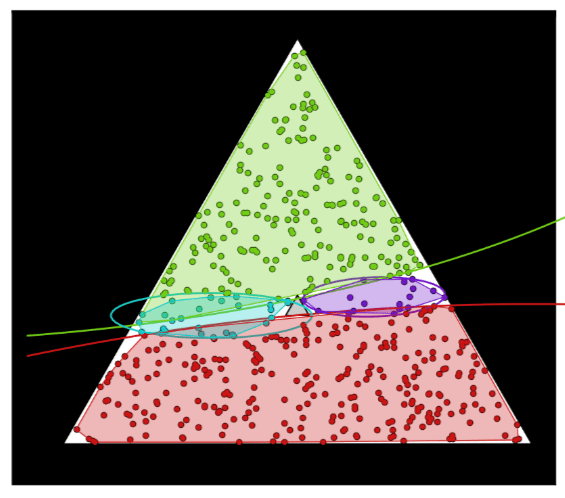
Addresses the Problem
Addresses the Problem
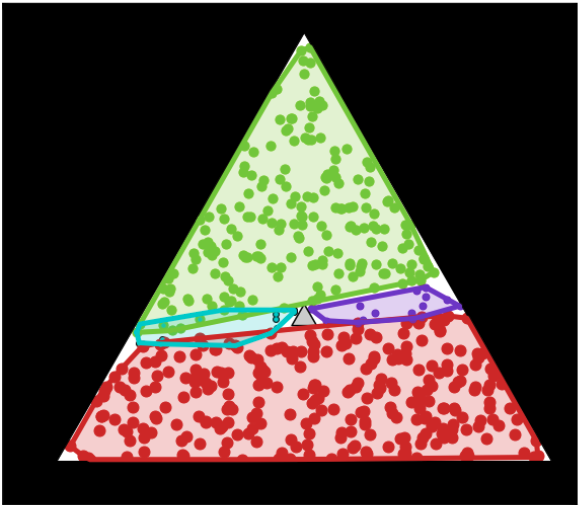
At the cost that Clique Cover now takes 20 times longer
Are All PartS of the Free Configuration Space Equal?
Big regions are not always useful
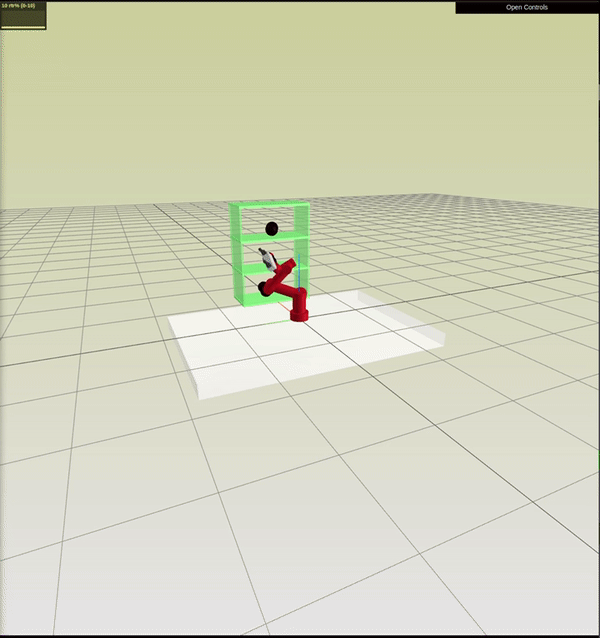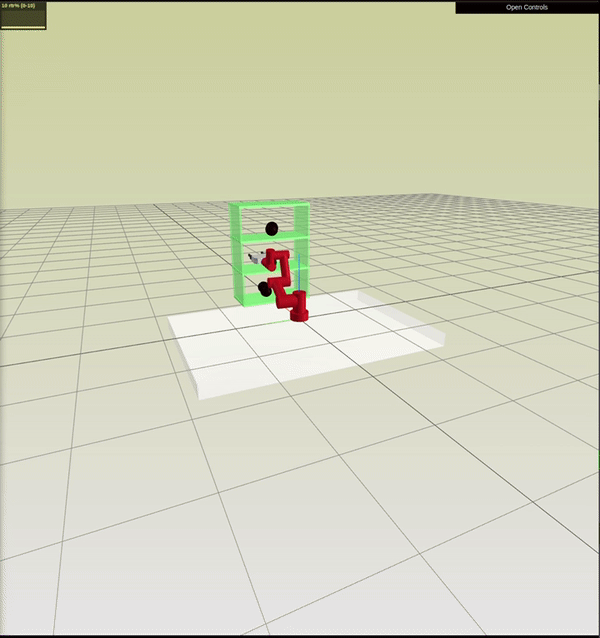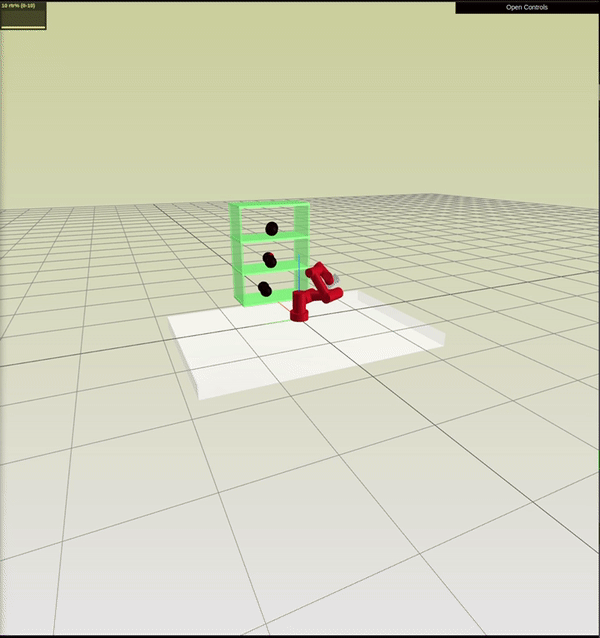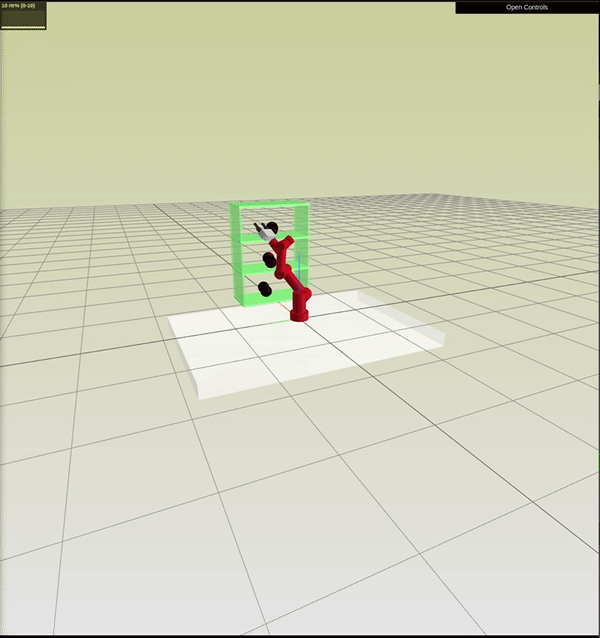
We Might only care about a Small portion of CSPACE
Reaching Into Shelves
Reaching Into Shelves
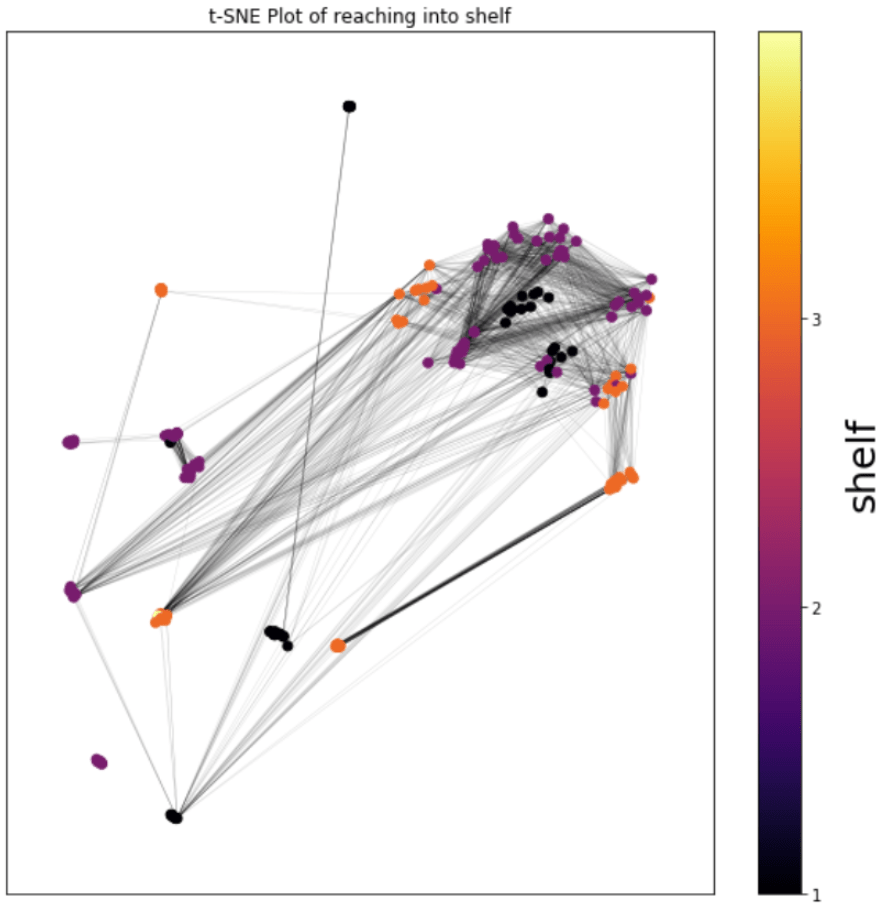
T-SNE + Visibility
Reaching Into Shelves
T-SNE + Visibility
- IK solutions form clusters
- Want coverage of very particular regions
- Dense sampling challenging for 7dof
Our Target C-Space is 14+ Dimensional
Proposal: Sample in Task Space
The Mode problem
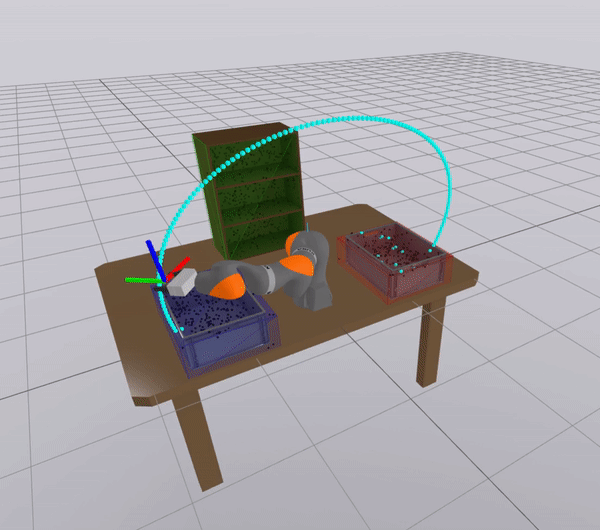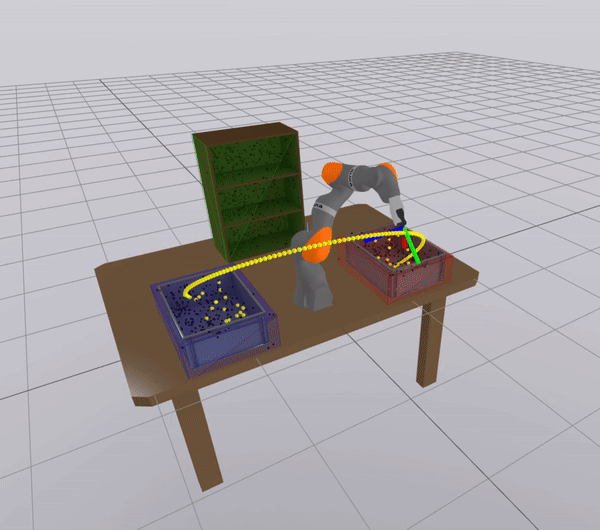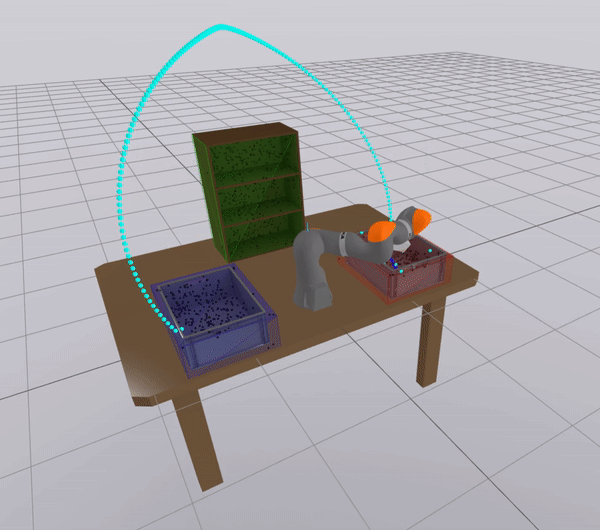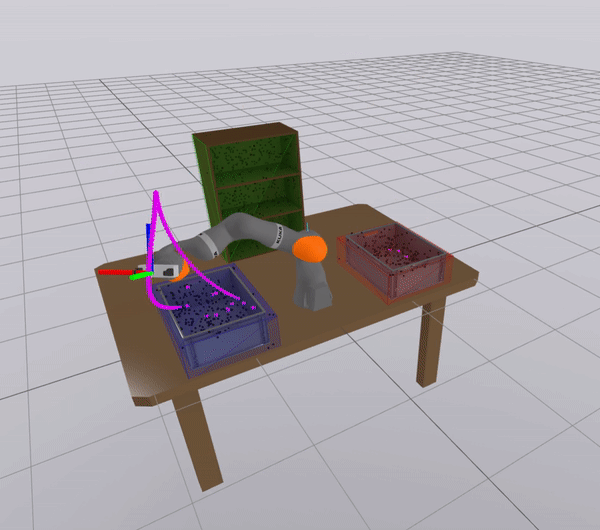
The Mode problem
unsupervised learning to clip long edges
results in better control for region growth
Task-Space Rapidly Exploring Random Tree
Voronoi Bias In Task Space
Promising
Recap
Extension Recap
Question 1: How can we put more geometric information in the clique cover to better approximate convex cover?
Question 2: How can we leverage task space to generate a better sampling distribution?
Concise Clique Covers Amazon
By Alexandre Amice
