Adapted Solvers For Graphs Of Convex Sets
Alexandre Amice
Amazon Fall 2025



Motivation: GCS is Very Flexible
Object Rearrangement
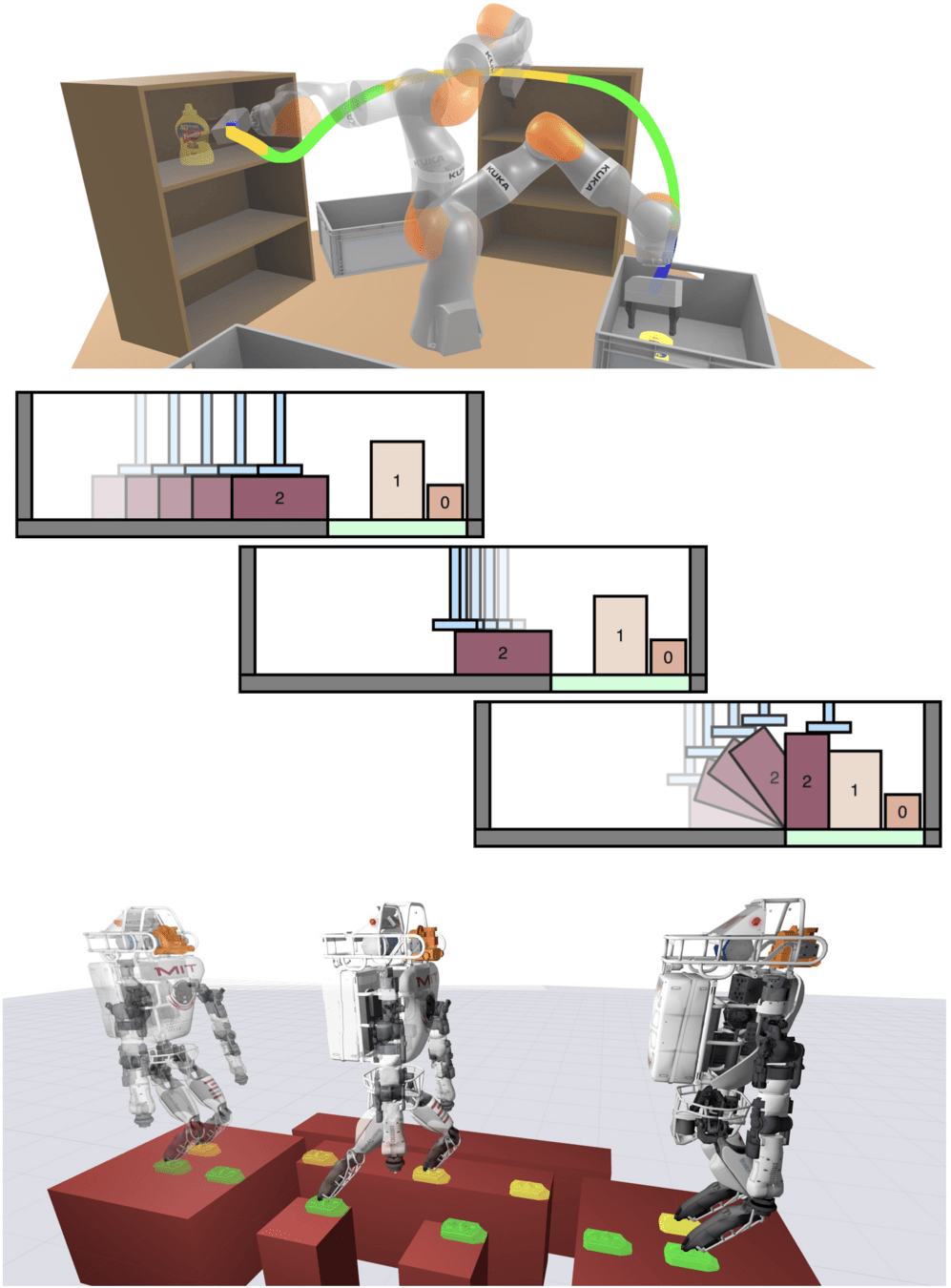
Motivation: GCS is Very Flexible
Object Rearrangement

Dynamic Motion Planning
Motivation: GCS is Very Flexible
Object Rearrangement


Dynamic Motion Planning
Contact Rich Manipulation
Motivation: GCS is Very Flexible
Object Rearrangement


Dynamic Motion Planning

More Complicated Graphs
More Complicated Sets
Contact Rich Manipulation
Complexity of Solving Methodology
A GCS with:
- n vertices
- Each vertex has m edges
- Each set has dimension d
Current State of the Art
Solver Wishlist
A GCS with:
- n vertices
- Each vertex has m edges
- Each set has dimension d
Target Complexity
Solver Wishlist
Target Complexity
Also Want
- Advances in graph algorithms should transfer
- Advances in convex optimization solvers should transer
- Naturally leverage HPC techniques like GPUs/Clusters.
Solve GCS at Any Scale
Object Rearrangement


Dynamic Motion Planning

More Complicated Graphs
More Complicated Sets
Contact Rich Manipulation
The Journey Of A GCS Problem
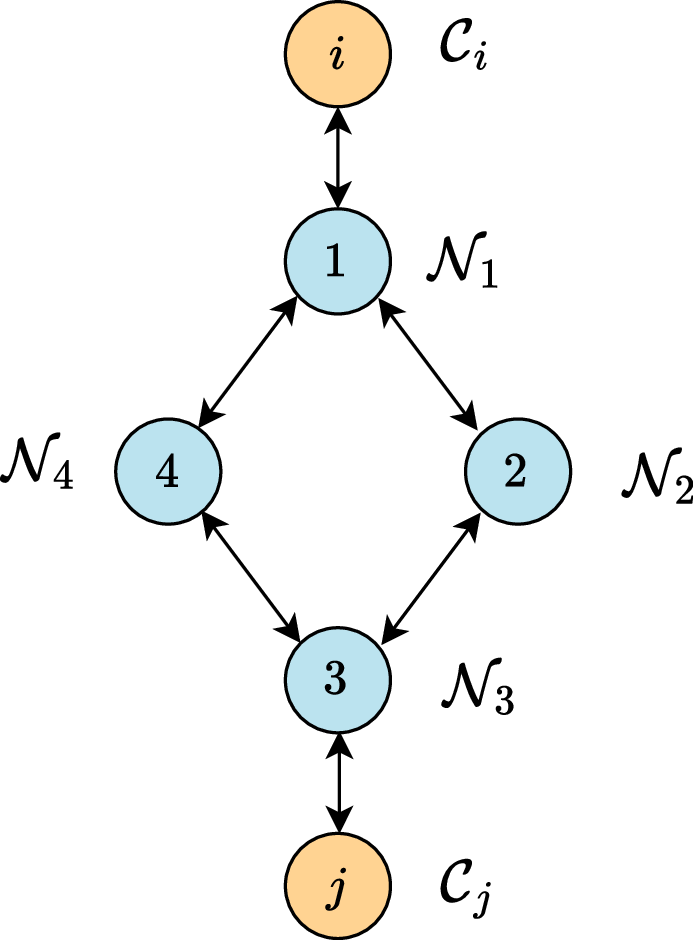
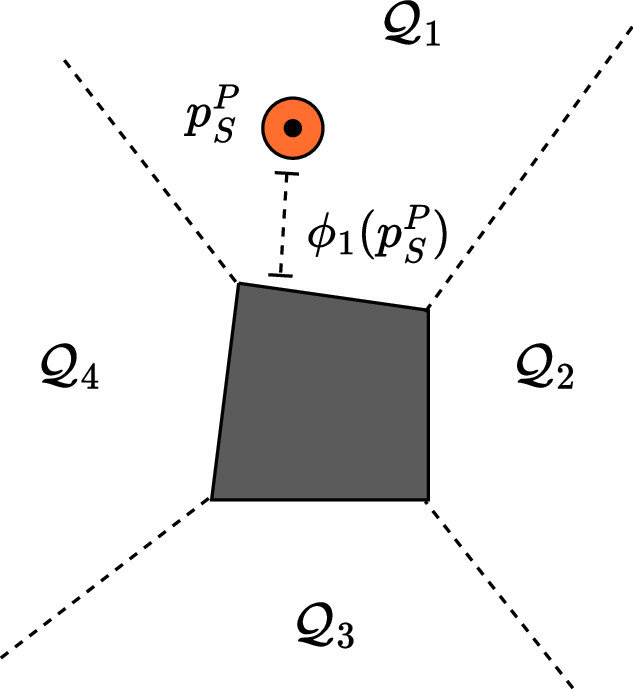
Problem
Model
The Journey Of A GCS Problem

Model
The Journey Of A GCS Problem
Model
Standardize
The Journey Of A GCS Problem
Model
Standardize
Form Relaxation
The Journey Of A GCS Problem
Model
Standardize
Form Relaxation
Parse To Conic Form
Solve

The Journey Of A GCS Problem
Form Relaxation
Parse To Conic Form
Destroys Structure
Form Relaxation
The Structure of The Relaxation
The Structure of The Relaxation
The Structure of The Relaxation
The relaxation keeps the graph and convex sets factored
The Structure of The Relaxation
Relaxation
Destroys Structure
-
Flattens a sparse, matrix optimization into a vector optimization.
-
Vector optimization is denser, more irregularly patterned, and worse conditioned.
-
Vector optimization obfuscates the role of the graph vs the convex sets
Lower Bound Work Per Iteration
Relaxation
Destroys Structure
A GCS with:
- n vertices
- Each vertex has m edges
- Each set has dimension d
Lower Bound
Lower Bound
An ADMM Based Solver For Gcs



Alternating Direction Method of Multipliers
A simple algorithm for solving problems of the form
Alternating Direction Method of Multipliers
Algorithm
1.
2.
3.
Alternating Direction Method of Multipliers
Alternating Direction Method of Multipliers
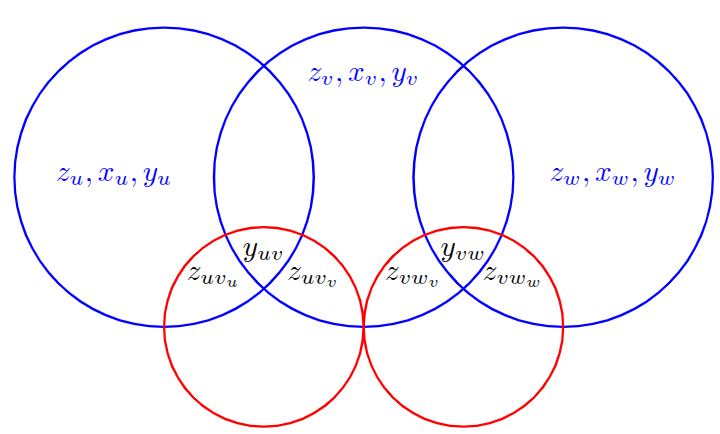
Alternating Direction Method of Multipliers
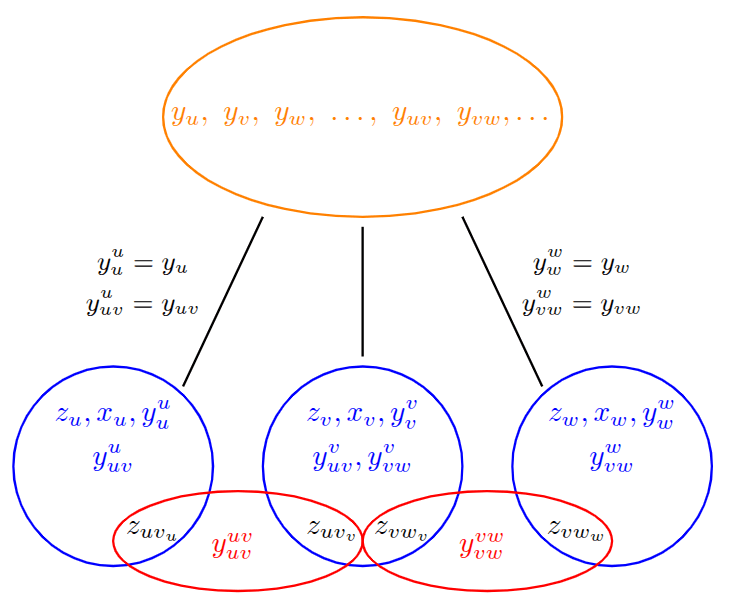
Separates the graph problem from the convex problem.
Alternating Direction Method of Multipliers
Separates the vertices from the edges
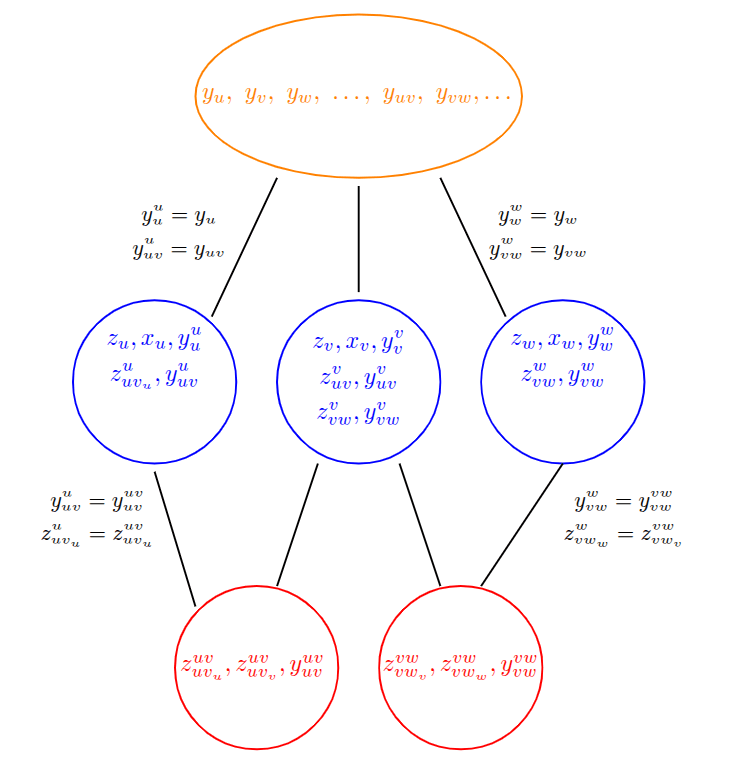
Alternating Direction Method of Multipliers
Algorithm
1.
2.
3.
1. Solve in parallel a conic program per vertex
2a. Solve in parallel conic program per edge
2b. Solve a graph problem
Alternating Direction Method of Multipliers
Algorithm
3.
1. Solve in parallel a conic program per vertex
2a. Solve in parallel a conic program per edge
2b. Solve a graph problem
Wish List
- Advances in graph algorithms should transfer
- Advances in convex optimization solvers should transer
- Naturally leverage HPC techniques like GPUs/Clusters.
Alternating Direction Method of Multipliers
Algorithm
3.
1. Solve in parallel a conic program per vertex
2a. Solve in parallel a conic program per edge
2b. Solve a graph problem
Work per iteration
- n vertices
- Each vertex has m edges
- Each set has dimension d
A GCS with
Requires
Alternating Direction Method of Multipliers
Algorithm
3.
1. Solve in parallel a conic program per vertex
2a. Solve in parallel a conic program per edge
2b. Solve a graph problem
- No need to solve steps 1 and 2 to optimality.
- Introduces a computation/communication trade-off
- Extreme cases can lead to closed form updates.
- Naturally supports branch-and-bound cuts
Additional Features
Alternating Direction Method of Multipliers
Algorithm
3.
1. Solve in parallel a conic program per vertex
2a. Solve in parallel a conic program per edge
Work per iteration
One Particularly Efficient Choice of Splitting
Requires
2b. Solve a graph problem
Runtime Per Iteration
Ours
- n vertices
- Each vertex has m edges
- Each set has dimension d
- With k processors
A GCS with
Scs/Cosmo Solver
Early Results On Mazes of Increasing Sizes
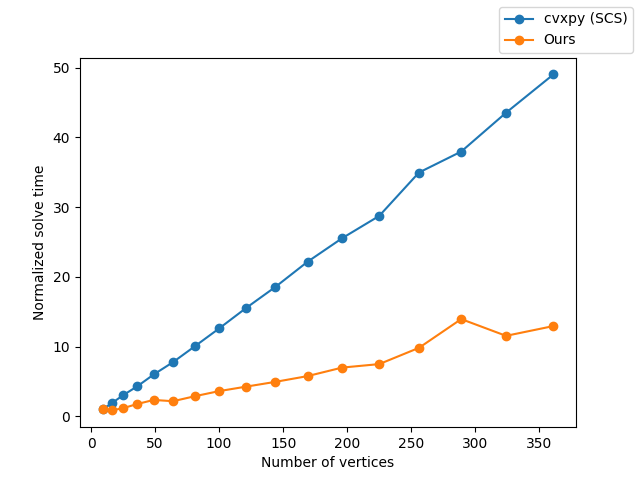
Early Results On Mazes of Increasing Sizes
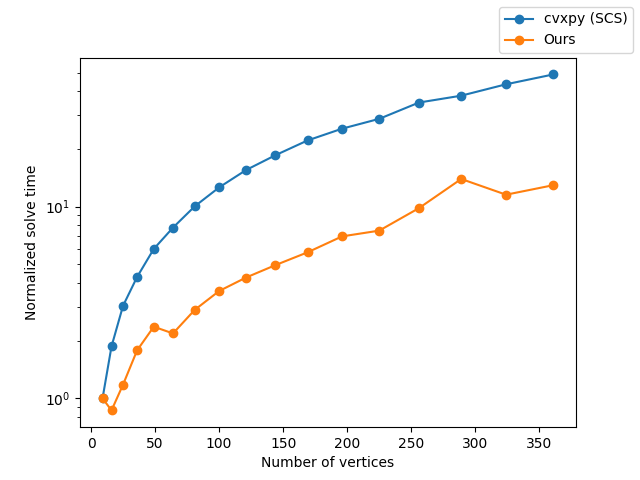
Solver Coming Soon
With GPU results...
An Interior Point Based Solver For Gcs



Similar Lessons Carry Through from ADMM to Interior Point
More soon
Form Relaxation
The Structure of The Relaxation
The Structure of The Relaxation
The Structure of The Relaxation
The Structure of The Relaxation
Form Relaxation
Destroys Structure
-
Flattens a sparse, matrix optimization into a vector optimization.
-
Vector optimization is denser, more irregularly patterned, and worse conditioned.
-
Vector optimization obfuscates the role of the graph vs the convex sets
Graph Of Convex Sets Final
By Alexandre Amice
Graph Of Convex Sets Final
- 121



