
Graph Of Convex Sets at Every Scale
Amazon Meeting Fall 2025
Alexandre Amice


Motivation
Text
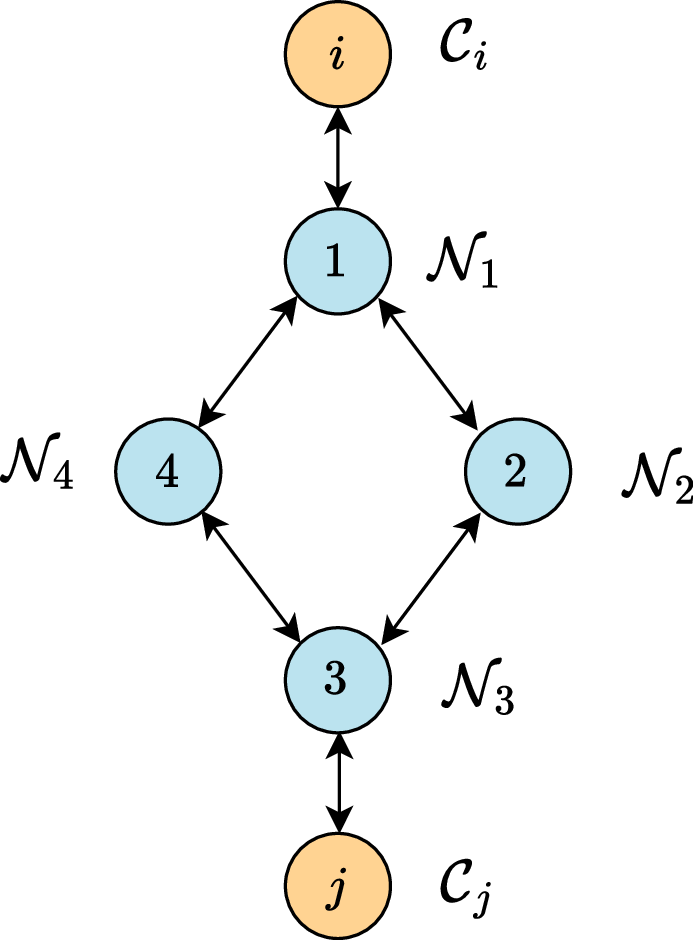
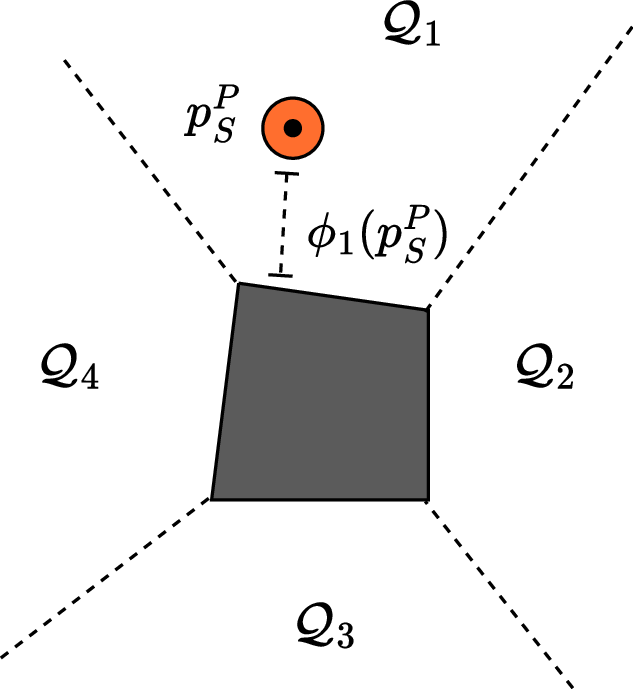
Problem
Model
The Journey Of A Graph of Convex Sets Problem

Model
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}y_{e}f_{e}(x_{u},x_{v})\\
\text{subject to }&
y_{v}x_{v} \in y_{v}\mathcal{X}_{v} ~\forall v \in \mathcal{V}
\\
&
y_{e}(x_{u}, x_{v}) \in y_{e}\mathcal{X}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
y \text{ encodes a path },~~ y\in \{0,1\}
\end{aligned}
The Journey Of A Graph of Convex Sets Problem
Model
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}y_{e}f_{e}(x_{u},x_{v})\\
\text{subject to }&
y_{v}x_{v} \in y_{v}\mathcal{X}_{v} ~\forall v \in \mathcal{V}
\\
&
y_{e}(x_{u}, x_{v}) \in y_{e}\mathcal{X}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
y \text{ encodes a path },~~ y\in \{0,1\}
\end{aligned}
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}c_{e}^{T}(z_{e_{u}},z_{e_{v}}, y_{e}) \\
\text{subject to }&
A_{v}z_{v}-b_{v} y_{v} \in \mathcal{K}_{v} ~\forall v \in \mathcal{V}
\\
&
A_{e}(z_{e_{u}},z_{e_{v}}) - b_{e}y_{e} \in \mathcal{K}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
A_{\mathcal{P}}y-b_{\mathcal{P}} \geq 0,~~ y\in \{0,1\}\
\end{aligned}
The Journey Of A Graph of Convex Sets Problem
Standardize
Model
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}y_{e}f_{e}(x_{u},x_{v})\\
\text{subject to }&
y_{v}x_{v} \in y_{v}\mathcal{X}_{v} ~\forall v \in \mathcal{V}
\\
&
y_{e}(x_{u}, x_{v}) \in y_{e}\mathcal{X}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
y \text{ encodes a path },~~ y\in \{0,1\}
\end{aligned}
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}c_{e}^{T}(z_{e_{u}},z_{e_{v}}, y_{e}) \\
\text{subject to }&
A_{v}z_{v}-b_{v} y_{v} \in \mathcal{K}_{v} ~\forall v \in \mathcal{V}
\\
&
A_{e}(z_{e_{u}},z_{e_{v}}) - b_{e}y_{e} \in \mathcal{K}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
A_{\mathcal{P}}y-b_{\mathcal{P}} \geq 0,~~ y\in \{0,1\}\
\end{aligned}
Standardize
Form Relaxation
The Journey Of A Graph of Convex Sets Problem
Model
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}y_{e}f_{e}(x_{u},x_{v})\\
\text{subject to }&
y_{v}x_{v} \in y_{v}\mathcal{X}_{v} ~\forall v \in \mathcal{V}
\\
&
y_{e}(x_{u}, x_{v}) \in y_{e}\mathcal{X}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
y \text{ encodes a path },~~ y\in \{0,1\}
\end{aligned}
\begin{aligned}
\min~& \sum_{e \in \mathcal{E}}c_{e}^{T}(z_{e_{u}},z_{e_{v}}, y_{e}) \\
\text{subject to }&
A_{v}z_{v}-b_{v} y_{v} \in \mathcal{K}_{v} ~\forall v \in \mathcal{V}
\\
&
A_{e}(z_{e_{u}},z_{e_{v}}) - b_{e}y_{e} \in \mathcal{K}_{e} ~ \forall (u,v) \in \mathcal{E}
\\
&
A_{\mathcal{P}}y-b_{\mathcal{P}} \geq 0,~~ y\in \{0,1\}\
\end{aligned}
Standardize
Form Relaxation
\begin{aligned}
\min~& g^{T}z \\
\text{subject to }~& Tx - s \in \mathcal{K}
\end{aligned}
Parse To Conic Form
Solve

The Journey Of A Graph of Convex Sets Problem
Graph Of Convex Sets at Every Scale
By Alexandre Amice
Graph Of Convex Sets at Every Scale
- 106



