Veto Power, Delegation and Mechanism Design
Brandon Williams
Alistair Wilson
Richard Van Weelden
Demand for Bad Policy Workshop
Bolzano
July 2025
Motivation
- Many "bargaining" contexts exist in which a less-informed party must decide what to offer to a more-informed party, who hold veto power
Motivation
- Many "bargaining" contexts exist in which a less-informed party must decide what to offer to a more-informed party, who hold veto power




Motivation
- Many "bargaining" contexts exist in which a less-informed party must decide what to offer to a more-informed party, who hold veto power
- The proposers:
- Can make simple take it or leave it offers
- Or, they can offer a range of options to the informed party, conceding some of their agenda-setting power




Literature
Models of similar bargaining forms have been proposed in theory...
- Under complete information - Romer and Rosenthal (1978)
- Under cheap talk negotiation - Matthews (1989)
- With valuable expertise involved - Holmström (1977)
- More recently: Kartik, Kleiner, Van Weelden (2021)
And used in experiments...
- Early bargaining - e.g. Roth and Murnighan (1980, 1982)
- Vetoes within committees - Kagel, Sung, and Winter (2010)
- Multiple rounds of bargaining - Nunnari (2021)
More recently: Kartik, Kleiner, Van Weelden (2021)
Theory
More recently: Kartik, Kleiner, Van Weelden (2021)
Theory: Take-it-or-leave-it
0
1
Proposer
- Proposer has:
- Increasing payoff \(\pi(z)\) over the outcome \(z\), for simplicity we'll assume this is linear
- Makes take-it-or-leave it offer \(y\)
- Vetoer has:
- ideal point \(\theta\) which is private information, \(\theta\sim F(\theta)\)
- Chooses \(z\in\left\{0,y\right\}\), either the veto threat point (here \(0\)) or the offer
\(y\)
\(\theta\)
Vetoer
Theory: Take-it-or-leave-it
\(\theta\)
Vetoer
0
1
Proposer
- Proposer has:
- Increasing payoff \(\pi(z)\) over the outcome \(z\), for simplicity we'll assume this is linear
- Makes take-it-or-leave it offer \(y\)
- Vetoer has:
- ideal point \(\theta\) which is private information, \(\theta\sim F(\theta)\)
- Chooses \(z\in\left\{0,y\right\}\), either the veto threat point (here \(0\)) or the offer
Theory: Offer Realization
0
1
Proposer, ideal
\(\tfrac{y}{2}\)
Offer \(y\)
These types veto
These types choose \(y\)
Theory: Offer Realization
0
1
Proposer, ideal
\(\tfrac{y}{2}\)
Offer \(y\)
These \(\theta\)-types veto
These \(\theta\)-types choose offer
\(z=y\)
\(z=0\)
Theory: TIOLI Realization
0
1
Proposer, ideal
\(\tfrac{y}{2}\)
Offer \(y\)
Suboptimal: Inefficient outcome, as \(\theta>y\), so higher outcome preferred by both
Breakdown: Inefficient as \(\theta>0\) preferred by both
Theory: TIOLI equilibrium
0
1
\(\tfrac{y}{2}\)
- Proposer increasing the offer \(y\) leads to:
- Marginal gain of \(\pi'(y)\cdot(1-F(\tfrac{y}{2}))\)
- Marginal loss of \(\left(\pi(y)-\pi(0)\right)\cdot \tfrac{1}{2}f(\tfrac{y}{2})\)
\(z=0\)
\(z=y\)
\(y\)
\(f(\theta)\)
Theory: TIOLI equilibrium
0
1
\(\tfrac{y}{2}\)
- Proposer increasing the offer \(y\) leads to:
- Marginal gain of \((1-F(\tfrac{y}{2}))\)
- Marginal loss of \(\tfrac{y}{2}\cdot f(\tfrac{y}{2})\)
\(z=0\)
\(z=y\)
\(y\)
\(f(\theta)\)
Theory: Delegation
\(\theta\)
Vetoer
0
1
Proposer
- Proposer:
- Offers set of options \(Y\)
- Vetoer has:
- Chooses \(z\in\left\{0\right\}\cup Y\), either the veto threat point (here \(0\)) or some offer in delegation set
Theory: Delegation Realization
0
1
\(\tfrac{y}{2}\)
Offer \(\left[y,1\right]\)
These types veto \(z=0\)
These types choose \(z=y\)
These types choose \(z=\theta\)
\(y\)
Theory: Delegation Realization
0
1
\(\tfrac{y}{2}\)
Offer \(\left[y,1\right]\)
\(y\)
No Suboptimality: Delegation option ensures this
Breakdown: Inefficient as \(\theta>0\) preferred by both, but smaller region than TIOLI
Theory: Delegation Equilibrium
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
- Proposer increasing the minimal offer \(y\) leads to:
- Marginal gain of \(\pi'(y)\cdot(F(y)-F(\tfrac{y}{2}))\)
- Marginal loss of \(\left(\pi(y)-\pi(0)\right)\cdot \tfrac{1}{2}f(\tfrac{y}{2})\)
Theory: Delegation Equilibrium
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
- Proposer increasing the offer \(y\) leads to:
- Marginal gain of \((F(y)-F(\tfrac{y}{2}))\)
- Marginal loss of \(\tfrac{y}{2}\cdot f(\tfrac{y}{2})\)
Theory: Delegation Equilibrium
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
- With increasing density we get a corner solution:
- coincide with TIOLI solution, \(y^\star=1\)
Theory: Delegation Equilibrium
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
- Or if we allow for offers above the maximum state we can get a solution
Theory: Delegation Equilibrium
- With decreasing density we get the other corner solution:
- Full delegation, with \(Y^\star=\Theta\) and \(z^\star=\theta\)
0
1
\(\tfrac{y}{2}\)
\(y\)
\(f(\theta)\)
Theory: Communication
- Communication is predicted to:
- Improve coordination in the take-it-or-leave it case (Matthews 1989)
- Do nothing in the delegation case (Kartik et al. 2021)
Experimental Design
- Constructed environment that models the veto bargaining framework
- One challenge: how to bring this abstract environment to a participants in a way that is easier to understand?
- To make the experiment tractable we:
- Discretize the state-space to 6 states with three distributions:
- Low (decreasing)
- Middle (modal distribution)
- High (increasing)
- Frame the decision as a Buyer/Seller problem:
- State is the Buyer's ideal demand
- Delegation is choice of a menu to offer
- Discretize the state-space to 6 states with three distributions:
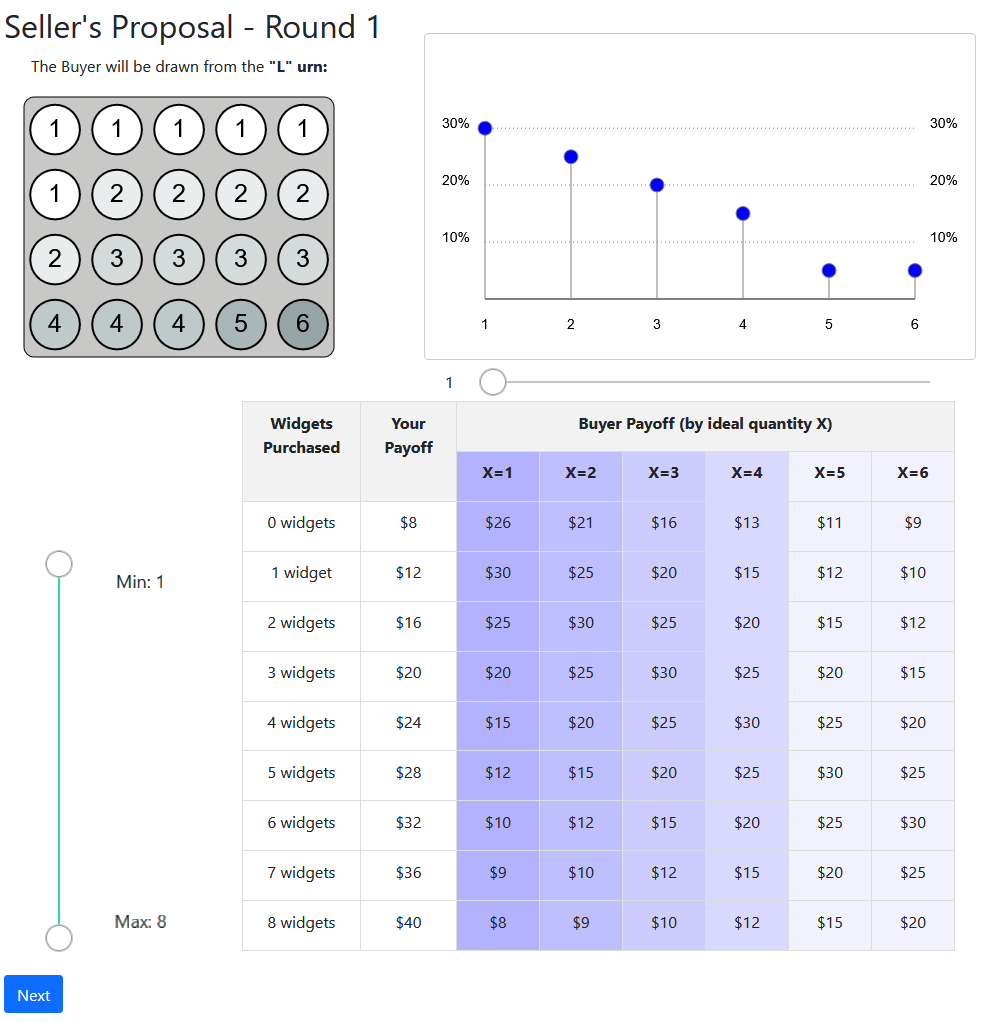



State introduced via an Urn
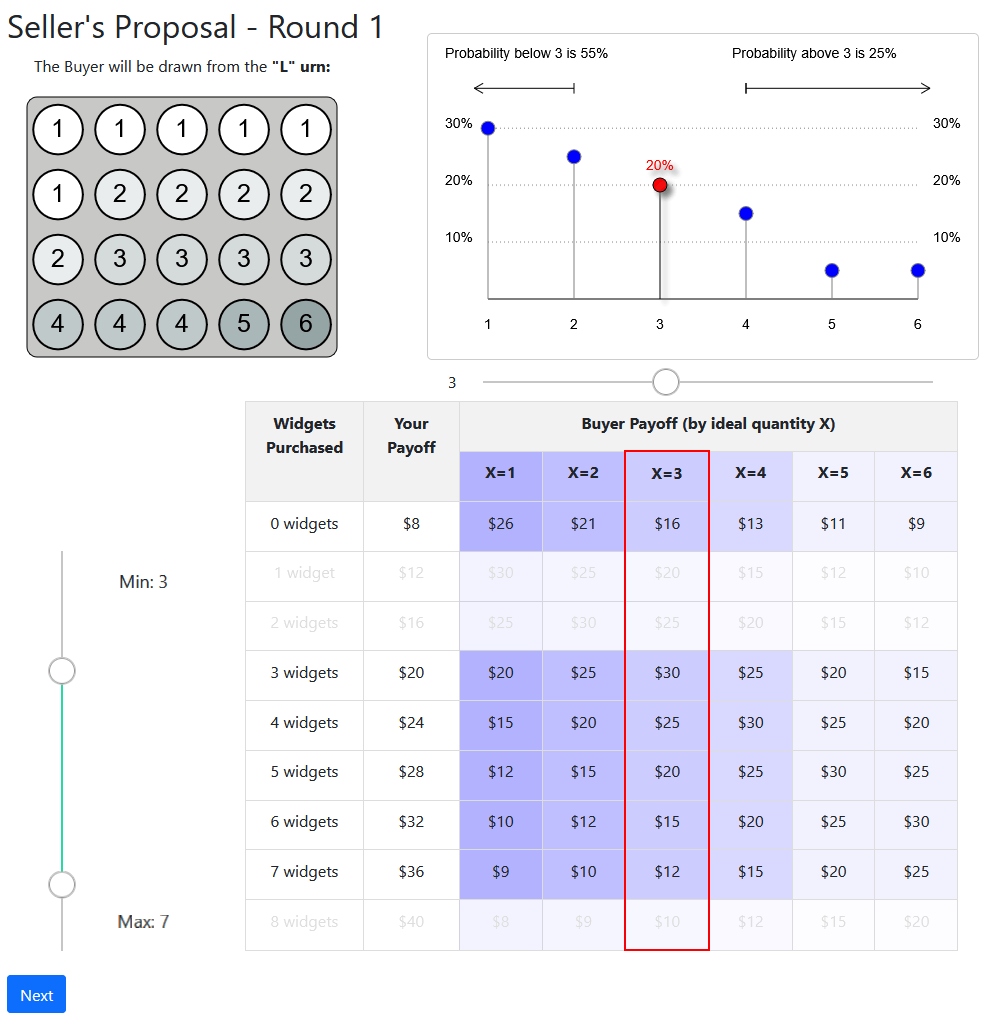
Delegation treatment:
offer a range
Take it or leave it:
single offer
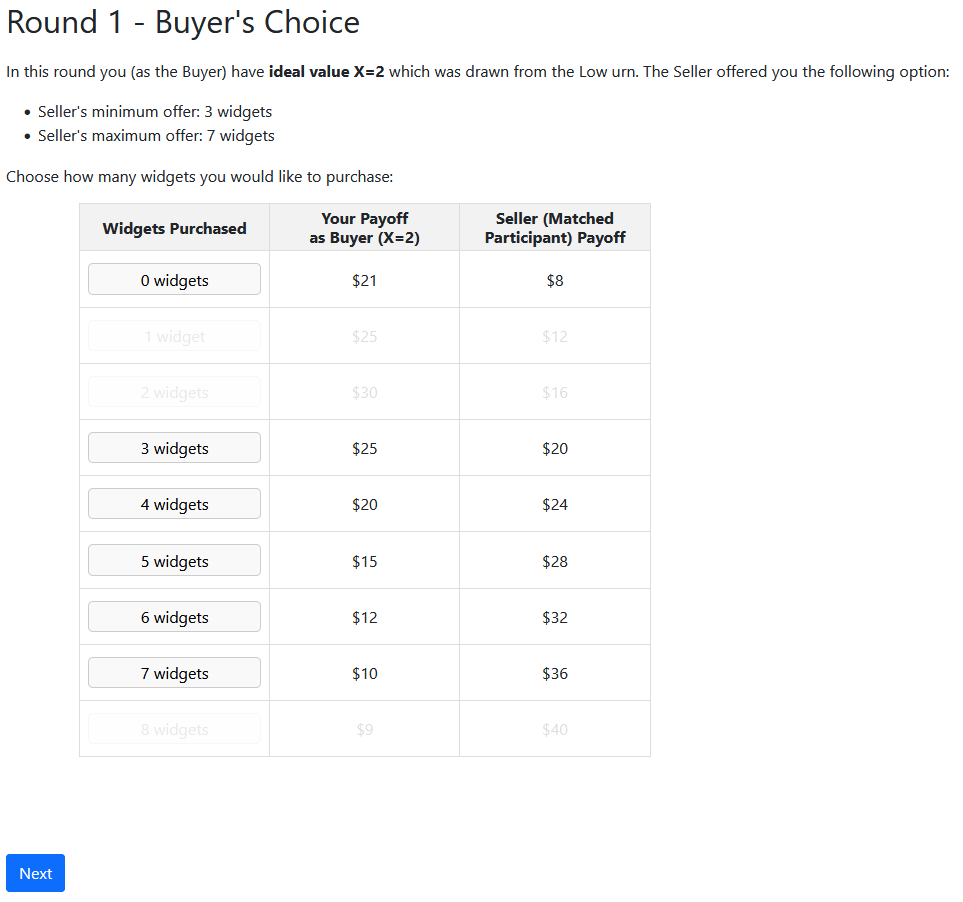
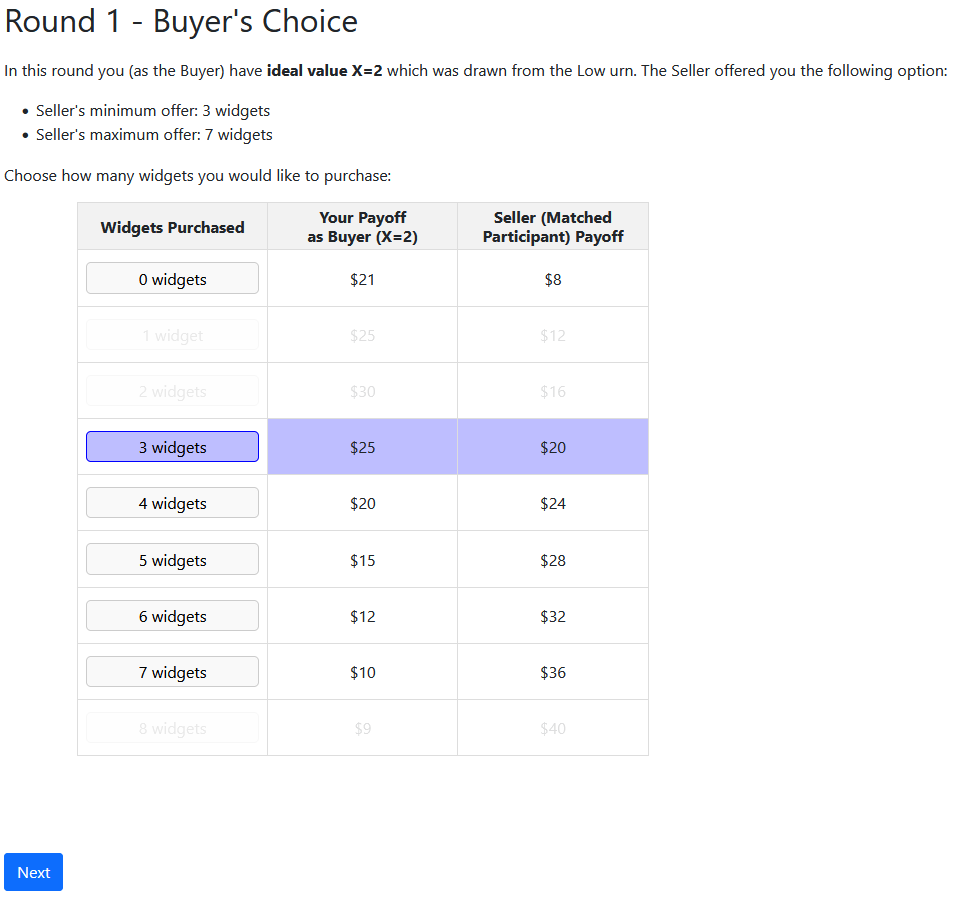
Experimental Design
- Within-subject variation:
- Varying distributions (high, middle, low) for the Buyer
- Changing roles: 5 rounds in one role, 5 rounds in the other, and back to first role for 5 more rounds
- Between subject 2x2
- 12 sessions at the Pittsburgh Experimental Economics Laboratory
- Collect other behavioral variables:
- Optimizing ability while playing against a robot Buyer
- Risk-aversion over the same domain
- Other-regardingness also over the same domain
Experimental Design
- Within-subject variation:
- Varying distributions (high, middle, low) for the Buyer
- Changing roles: 5 rounds in one role, 5 rounds in the other, and back to first role for 5 more rounds
- Between subject 2x2:
- 12 sessions at the Pittsburgh Experimental Economics Laboratory
| No Chat | Chat | |
|---|---|---|
| TIOLI | N=66 |
N=60 |
| Delegation | N=64 |
N=66 |
Predictions: Seller outcome
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | -12% | 0% |
| Middle | 7% | 10% |
| High | 18% | 18% |
Relative to full delegation:
So we should see a decreasing gain to seller as the distribution shifts
Predictions
| Dist. | Breakdown | Suboptimal | Breakdown | Suboptimal |
|---|---|---|---|---|
| Low | 55% | 5% | 0% | 0% |
| Middle | 25% | 10% | 25% | 0% |
| High | 25% | 0% | 25% | 0% |
TIOLI
Delegation
So we a decrease in efficiency between TIOLI and Delegation, and the disappearance of suboptimal positive outcomes
Results
- Buyer behavior is almost always self-maximizing:
- 90% in TIOLI, 88% in Delegation
- Of the remainder \(\sim\)75% is Generous to the Seller

Results: Seller offers in TIOLI



Low
Middle
High
Results: Seller offers in TIOLI

Results: Seller offers in Delegation
Low
Middle
High



Minimal offer in interval:
Results: What else is included in interval?

Results: Seller offer Comparison


TIOLI
Delegation
Results: Offer comparison over Mechanisms
Low



Middle
High
In the No Communication games we find that:
- Well-ordered behavior across the distributions
- More spread across than the point prediction
- Lower minimal offers in Delegation, more than expected in High
General behavior
Results: Inefficiency (Theory)

TIOLI
Delegation
Results: Inefficiency (Data)

TIOLI
Delegation
Results: Outcomes
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | -12% | 0% |
| Middle | 7% | 10% |
| High | 18% | 18% |
Theory relative to full delegation:
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | -14% | 1% |
| Middle | -7% | 4% |
| High | 3% | -7% |
Actual:
Effect of Delegation: Theory

Effect of Delegation: Empirical Payoffs

We find that:
- Delegation \(\succ\) TIOLI
- We find this for all distributions:
- even increasing!
- Most of the efficiency gains are captured by the Responder
- Best improvement for Proposer in decreasing distribution
Efficiency
Results: Inefficiency (Data with No Comm)

TIOLI
Delegation
Results: Inefficiency (Data with Comm)

TIOLI
Delegation
Results: Communication Offers (TIOLI)



Low
Middle
High



Chat
No Chat
Results: Offers (Delegation)



Low
Middle
High



Chat
No Chat
Results: Outcome \(z\), relative to Full deleg
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | -14% | +1% |
| Middle | -7% | +4% |
| High | +3% | -7% |
Without Chat:
| Dist. | TIOLI | Delegation |
|---|---|---|
| Low | +20% | +13% |
| Middle | +13% | 0% |
| High | +8% | +5% |
With Chat:
We find that:
- Communication substantially improves bargaining efficiency in both mechanisms
- Proposers do worse in the Delegation case
Communication
Diagnosing the Failures
At the end of the experiment the participants make choices across a number of decision problems:
- A pure optimization problem
- A lottery choice
- An other regarding choice
Diagnosing the Failures: Pure Optimization
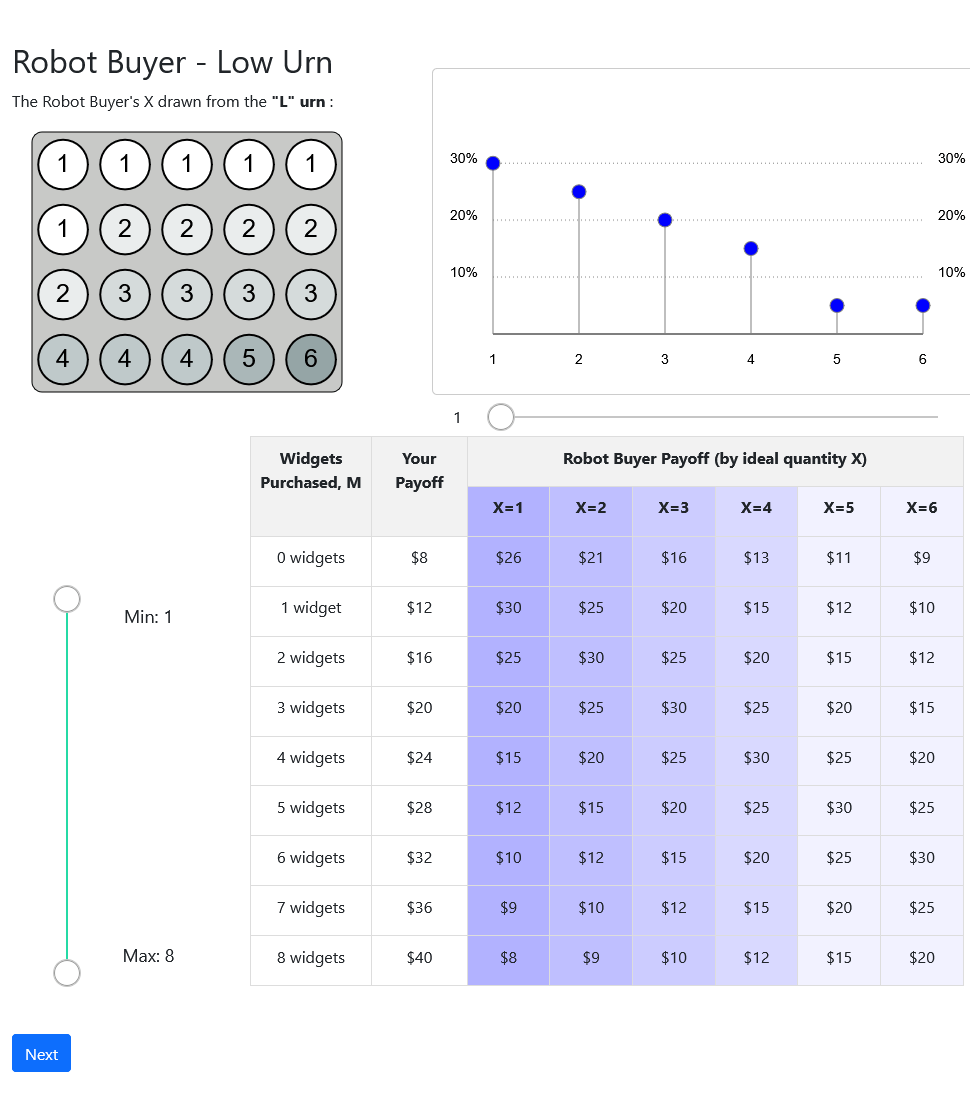
Diagnosing the Failures: Lotteries
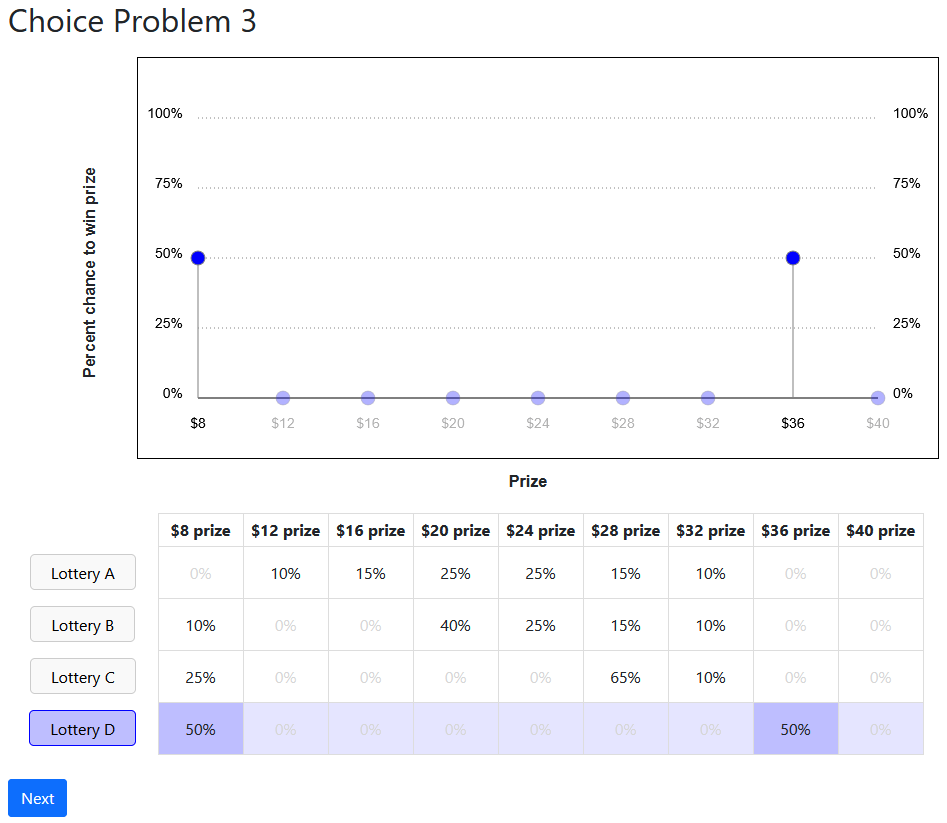
Diagnosing the Failures: Distribution
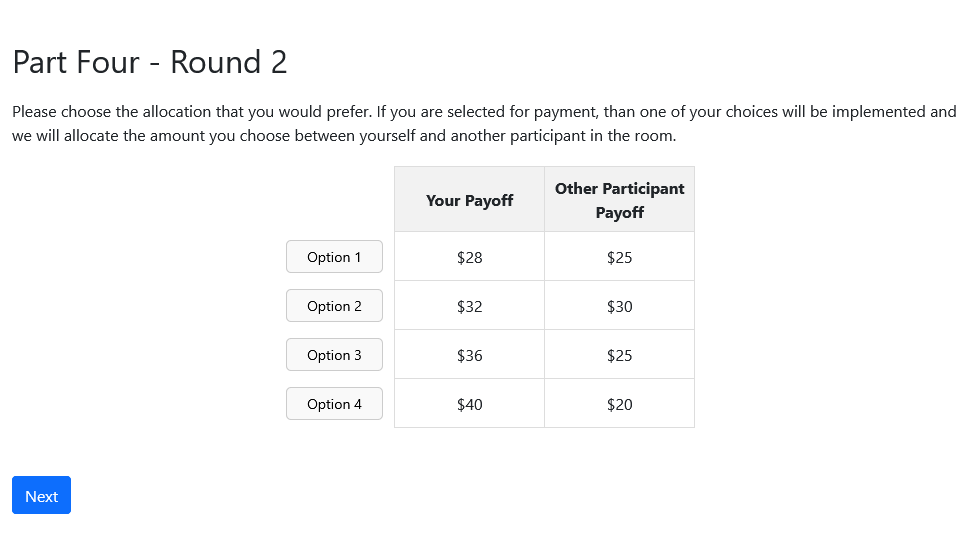
Diagnosing the Failures: Results
Using the decision problems we can begin to understand where deviations are coming from:
- Risk preferences
- Other-regardingness
- Optimization failure
So far the results are only preliminary but:
- Main reason sellers don't extract more of the delegation gain is optimization failure
- Lottery choices indicate less delegation
- Robot choices match behavior in the Delegation game
Conclusion
- Test delegation bargaining with veto power in a lab setting
- Sellers respond to key distribution parameters
- Clear efficiency gains from the delegation mechanism over take-it-or-leave-it offers
- But more of the surplus goes to the responder
- Both mechanisms are highly efficient with open communication, but proposers do better here without the delegation option
- Optimization failures in understanding the mechanism action space underly the proposer's failure to extract more.
- However, this doesn't lead to inefficiency as they over-delegate
Thank you!
Questions or Comments?
Delegation
By Alistair Wilson
Delegation
- 76


