Neural Tangent Kernels
UBC MLRG - March 9 2022
Amin
Artificial Neural Networks
- Over-parameterization leads to fewer "bad" local minimas
- They are paradoxical, as we expect an overparameterized model to interpolate and not have good generalization power
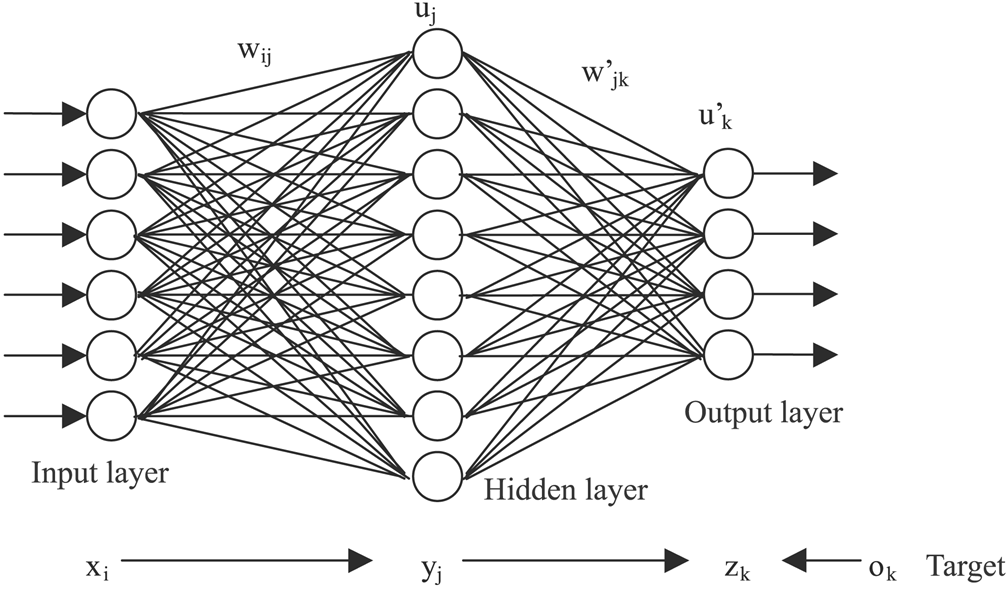
- Not much information about why they have such a good generalization power
Neural Networks in Function Space
Arthur Jacot, Franck Gabriel, Clement Hongler
Neural networks in Function space
- Loss landscape of the problem of optimizing a neural networks' parameters is highly non-convex, this doesn't allow us to be able to easily analyze their training dynamics
-
Idea: Study neural networks in the function space!
- For Squared loss, the functional loss landscape will be convex
- But how do we associate optimization in the functional space with optimization in the weight space?
Neural Networks in Function Space: Definitions
Input dataset is fixed:
We refer to the notion below as all the functions in our function space:
On this space, we use the following seminorm:
p^{in} = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\}: \frac{1}{N} \sum_{i=0}^N \delta_{x_i}
\mathcal{F} = \{f: \mathbb{R}^{n_0} \to \mathbb{R}^{n_L}\}
{\langle f, g \rangle}_{p^{in}} = \mathbb{E}_{x \sim p^{in}} [{f(x)}^T g(x)].
Neural Networks in Function Space: Definitions
The cost function is defined as
We can define the dual space of all functions as . This is the set of all such that .
Thus, each member of this dual class can be written as
for some d in the Function Space!
C(f) = \frac{1}{N} \sum_{i=1}^N{(f(x_i) - y_i)^2}
\mu = {\langle d, \cdot \rangle}_{p^{in}}
{\mathcal{F}}^*
\mu
\mu: \mathcal{F} \to \mathbb{R}
Neural Networks in Function Space: Loss function
Now let's derive loss function's derivative with respect to function! Note according to the definition below, as the dataset is fixed, the value of cost function only depends on the values of f!
Cost function derivative is:
Note that this is a member of , as it maps an input f to a real number!
C(f) = \frac{1}{N} \sum_{i=1}^N{(f(x_i) - y_i)^2}
\partial_f^{in} C|_{f_t} (f) = \frac{2}{N} \sum_{i=1}^{N} f(x_i)^\top \left(f_t(x_i) - y_i \right) = {\langle d|_{f_t}, f \rangle}_{p^{in}}
{\mathcal{F}}^*
One more (last) definition:
Kernel Gradient
The Neural Tangent Kernel
If we write out the expressions, turns out that neural networks trained using gradient descent evolve according to Kernel Gradient Descent, with a specific kernel called "Neural Tangent Kernel":
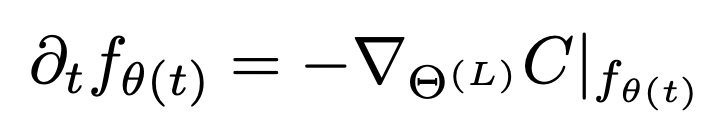
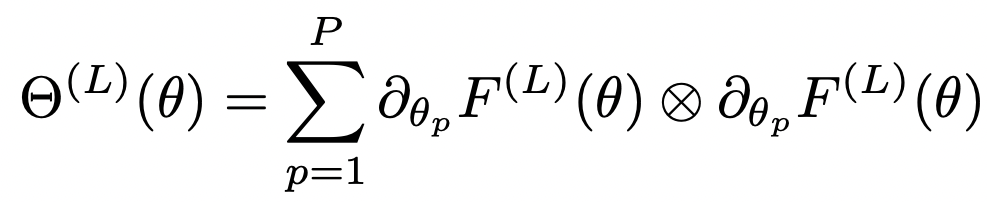
Now that we have this, are we done with our analysis?
The Neural Tangent Kernel
Jacot et al. 2018 showed that for fully connected neural networks at initialization, when the width of the network goes to infinity, the NTK converges in probability to a deterministic limiting kernel.
Moreover, they showed that this kernel stays the same during the training phase!
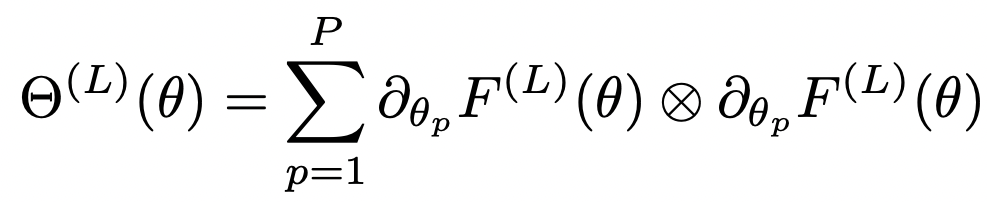
Neural Network Dynamics in the infinite width limit
As a consequence, in this limit, the dynamics of the neural network can be explained through a differential equation:
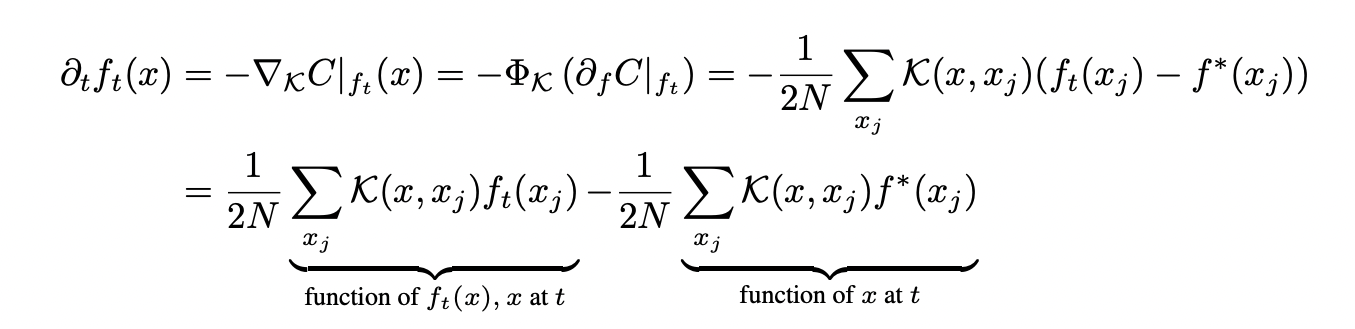
Neural Network Dynamics in the infinite width limit
If we solve this differential equation, we'll see that the network function evolves according to the following dynamics while trained using gradient descent:
Thus, we can analytically characterize the behaviour of infinitely wide (and obviously, overparameterized) neural networks, using a simple kernel ridge regression formula!
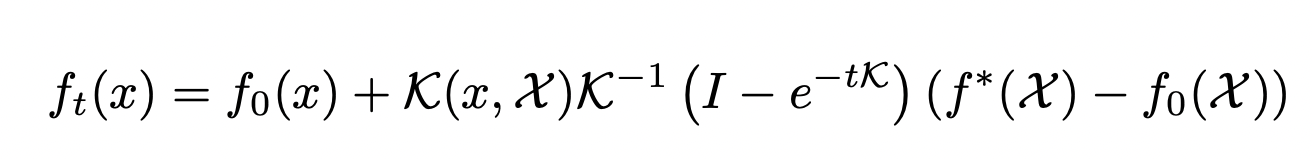
What about finite networks?
What about finite networks?
Arora et al. 2019 showed that under some regulatory conditions, for any and , for any width, with probability at least 1- , we have:
where L can be determined using the width, and .
This suggests that as the width grows, the NTK of the network gets more similar to the NTK of the corresponding infinite width network.
\delta
\epsilon
\delta
\delta
\epsilon
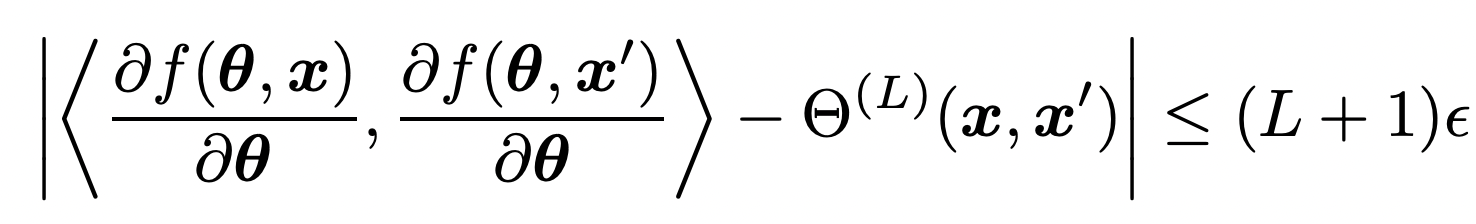
What about finite networks?
They also showed that under some regulatory conditions, for any and , for any width, with probability at least 1- , we have:
where is the kernel ridge regression using the "empirical" NTK evaluated using the network.
\delta
\epsilon
\delta
f_{ntk}
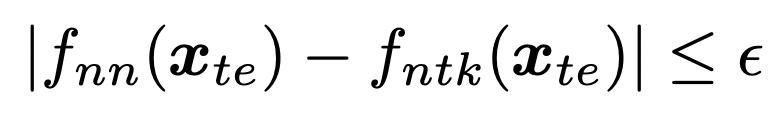
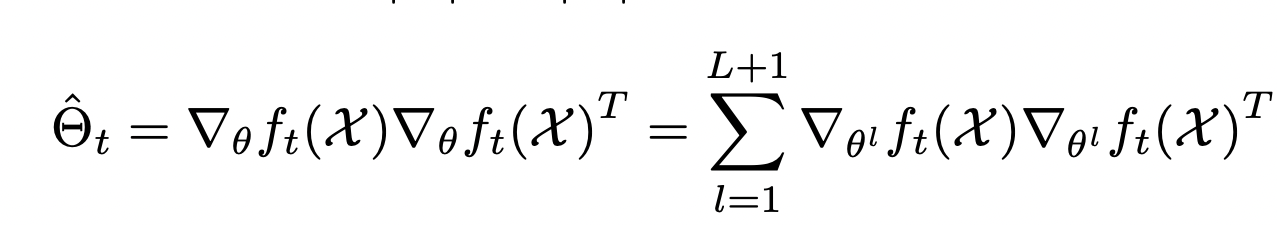
Linearized Neural Networks
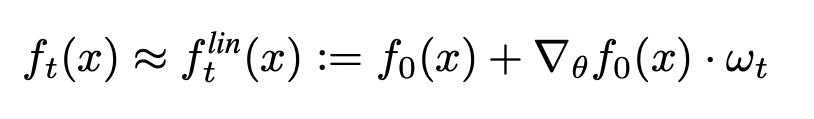
Linearized Neural Networks
Lee et al. showed that the training dynamics of a linearized version of a neural network can be explained using kernel ridge regression with the kernel as the empirical Neural Tangent Kernel of the network:
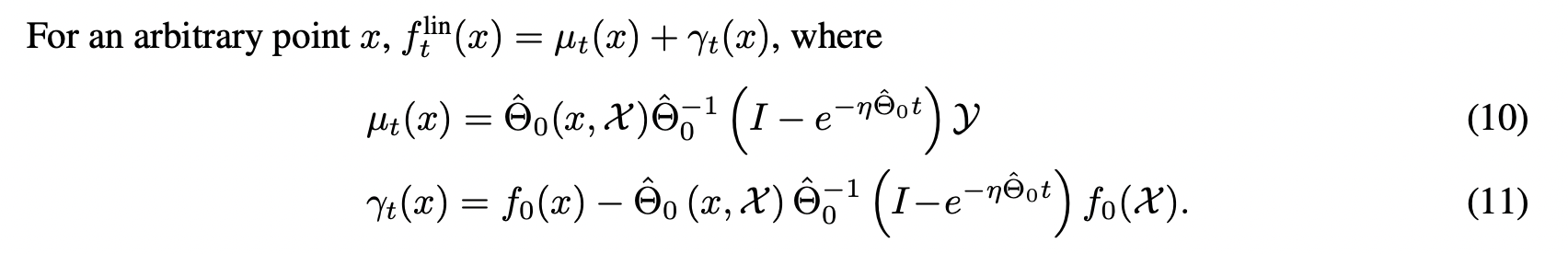
Linearized Neural Networks
Moreover, they showed corresponding bounds between the predictions of the actual network, and the linear network:
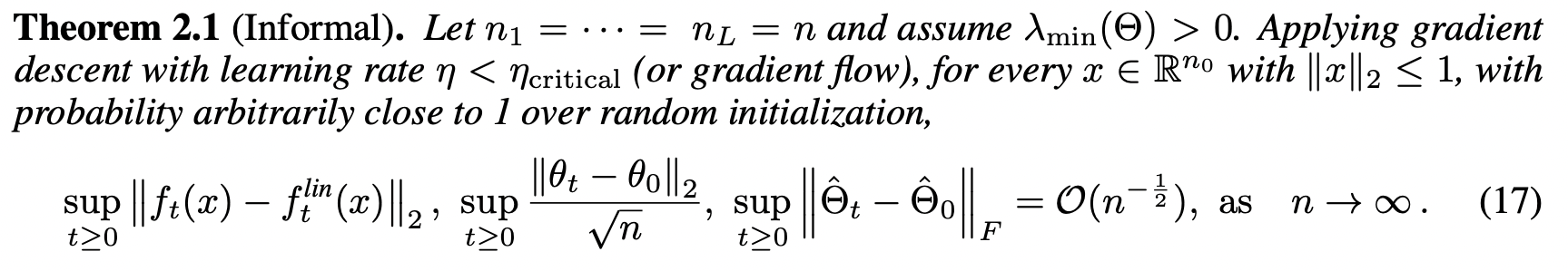
What about more complex architectures?
Thanks!
Neural Tangent Kernels
By Amin Mohamadi
