Registering Medical Images
Application to Glioblatomas
Anton François
suppervised by
Joan Glaunès & Pietro Gori


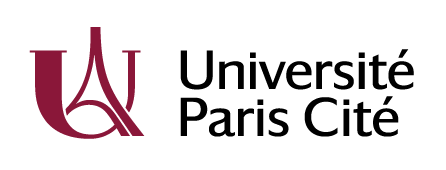

About Me :
- Bachelor Frontier of Life Science (FdV) at CRI
- Bachelor Mathematics and Simulation at Paris Descartes
- Master in Mathematic, Modelisation and Learning at Paris Descartes
- PhD : Registering Images with topological variation. Application to glioblastomas atlases construction in cerebral imagery.
2012-2015
2014-2016
2016-2019
2019-2022



Main Line Project
Creating Glioblastomas Atlases
Statistical Altas : [Roux, 2019] Frequence of apparition by voxels.
Anatomical Atlas : [Beg and Khan, 2005] Average shape.
Topological Altas : Collection of homeomorphisms covering a topological space (ex: manifold)
Definition
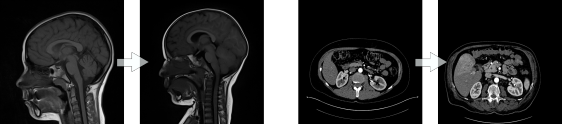
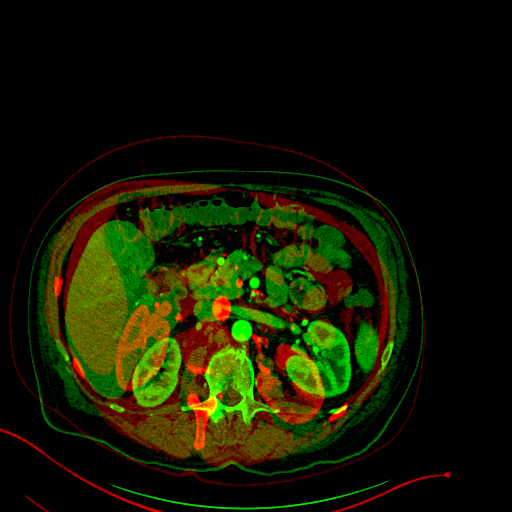
Normalisation of medical images is a important step for data acquisition

Before
linear registration :
After
Non Linear registration
Diffeomorphic matching => Keeps the Topology
Constant Vector fields
- Dartel [Ashburner 2007]
- Demons [Vercauteren et al 2009] [Lorenzi et al 2013]
Temporal vector field
- LDDMM [Trouvé 1995] [Christensen et al. 1995] [Beg et al. 2005]



LDDMM
Comparing the amount of deformation in between two images.
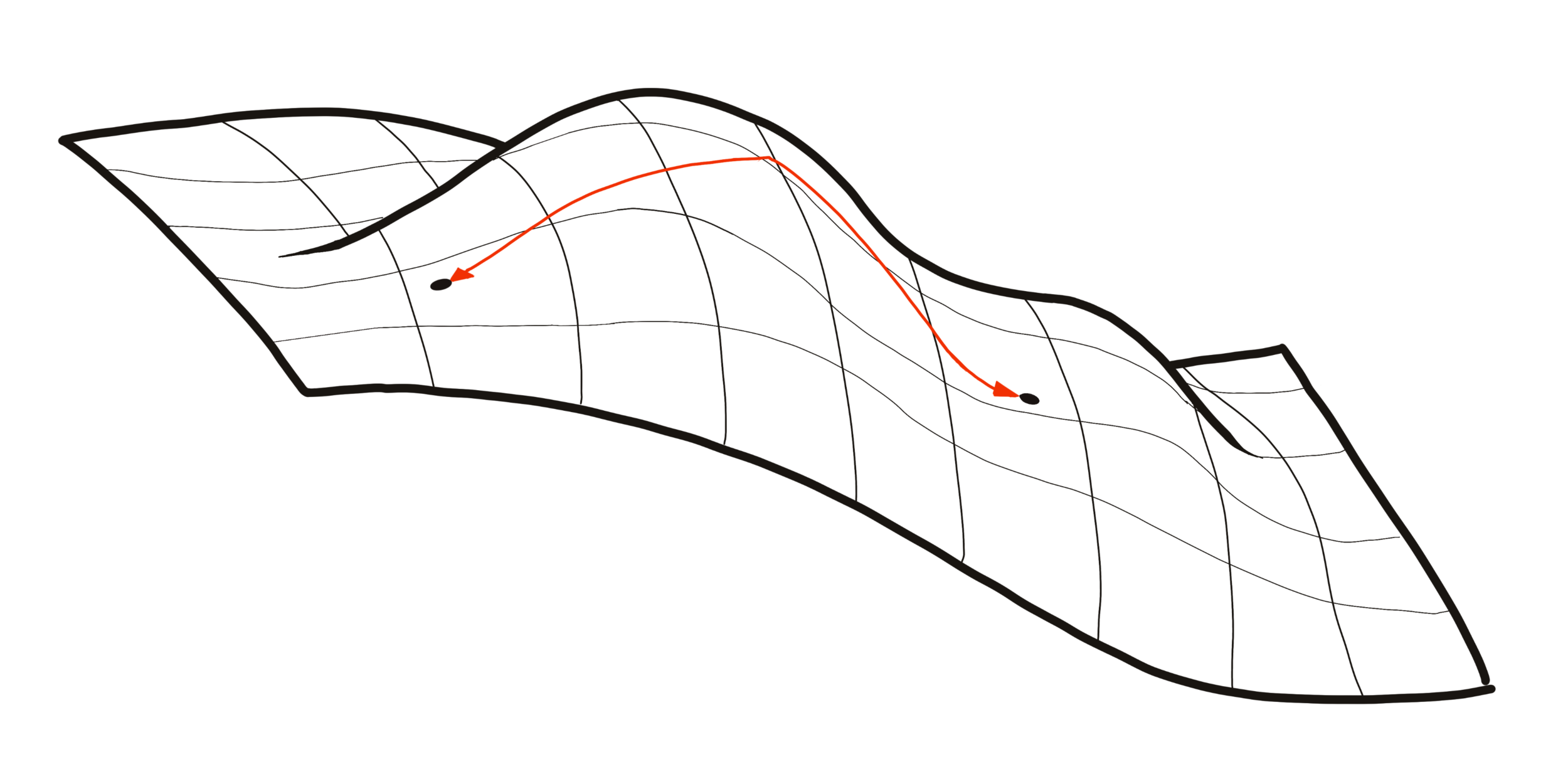




LDDMM

Image \(I\) deformed by a temporal vector field \(v = (v_t)_{t\in [0,1]}.\)
\[ \dot I_t = v_t \cdot I_t \]





LDDMM

Energy of the deformation generated by \(v\)
$$\mathcal E(v) \doteq \frac12 \int_0 ^1 \|v_t \|_V^2dt = \frac12 \int_0 ^1 \langle v_t , K_\sigma \star v_t \rangle_2 dt $$
\(K_\sigma \star \) being the convolution with a Gaussian kernel.
Distance between two images
$$d(I,J) = \mathrm{min}_{v} \mathcal E(v), \qquad \text{s.t. }I_0 = I; I_1 = \int_0^1 v_t \cdot\nabla I_t dt = J$$
Geodesic := shortest path on a Manifold
To find the minimum of this cost :
$$ E(v,I) = \frac12 \left\| I_1 - T \right\|_2^2 + \frac12\int_0^1 \|v_t\|_V^2 dt $$
We have to integrate over this set of geodesic equations :
$$\left\{\begin{array}{rl}v_t &= -\frac{\rho}{\mu} K_\sigma \star (z_t \nabla I_t)\\ \partial_t z_t &= -\quad \nabla \cdot (z_t v_t) \\ \partial_t I_t &= -\langle v_t , \nabla I_t\rangle\end{array}\right.$$
Advection equation
Continuity equation

LDDMM



Karcher mean : The average Atlas builder.
Given a group of image \(I^1,\dots,I^n\) and the Riemannian metric \(d\) we compute the template \(I\) by minimising:
$$\mathcal M(I) = \frac{1}{2n} \sum_{k=1}^{n} d(I,I_1^k)^2$$

Metamorphosis := Diffeomorphic registration + Intensity changes
[Trouvé, 2005]
deck
By Anton FRANCOIS
deck
- 365



