Demeter Metamorphosis

A python Library

 

Anton François

Joined work with

Joan Glaunès & Pietro Gori & Alain Trouvé

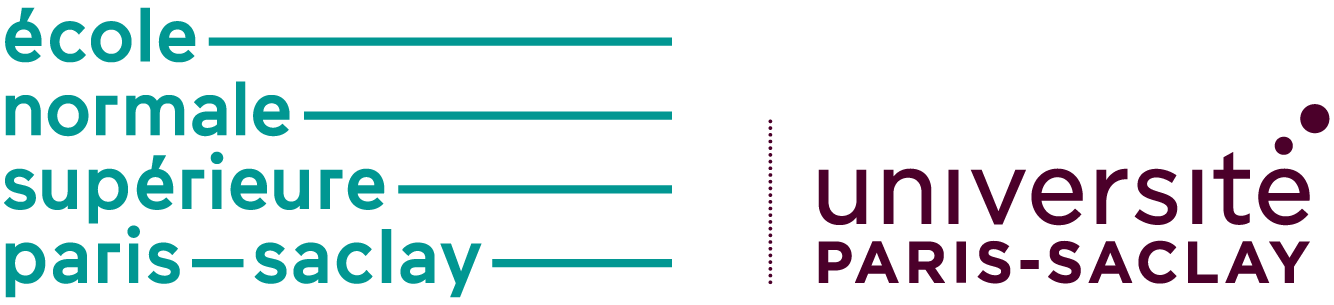
github.com/antonfrancois/Demeter_metamorphosis

Anton François - 12/02/2025

  • Image registration:
    • Topology Preserving OR not
    • 2D and 3D images
    • based on PyTorch for GPU and auto-diffentiation
    • Different Models of Metamorphosis

Why ?

github.com/antonfrancois/Demeter_metamorphosis

Anton François - 12/02/2025

How to use these slides:

1.At the first level (click on the left) -> Theory

2.If arrow down

 

a.Hints on how to implement that in Demeter.

b. A mission !

Don't hesitate to leave me an issue:

~ 15min presentation

~ 35min tutoriel

Mission example (level 0) :

- Find this page

Documentation example.

github.com/antonfrancois/Demeter_metamorphosis

Anton François - 12/02/2025

# activate the environement you created

# go in Demeter Folder
cd Demeter_metamorphosis

# update the package by pulling
git pull

Please update the package!

from LDDMM to Metamorphosis

Background

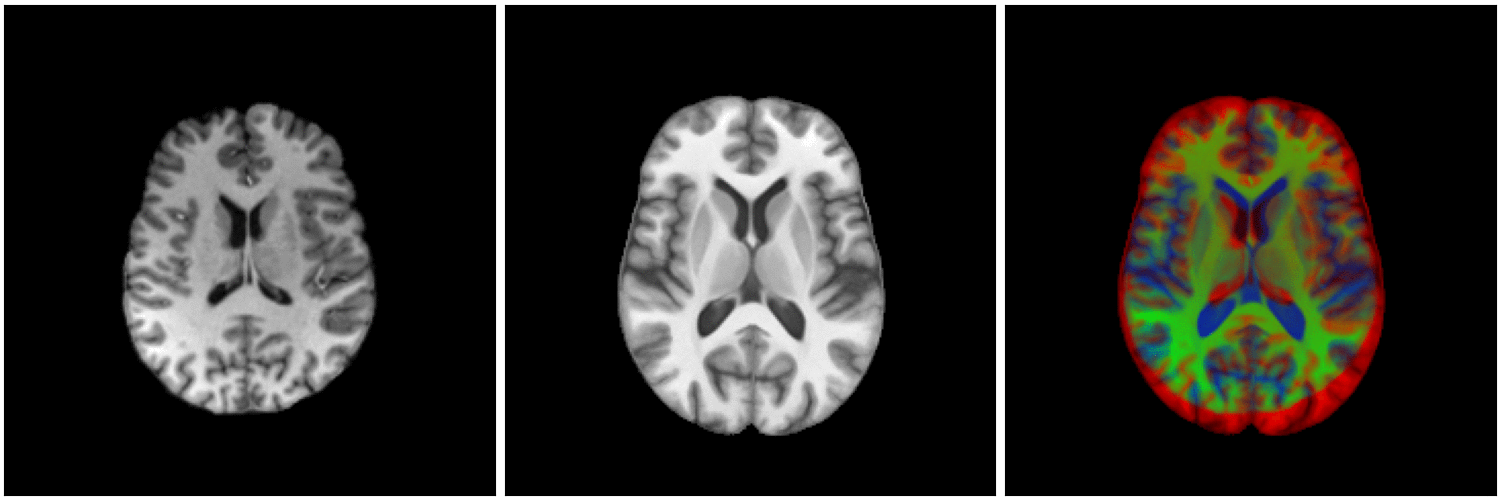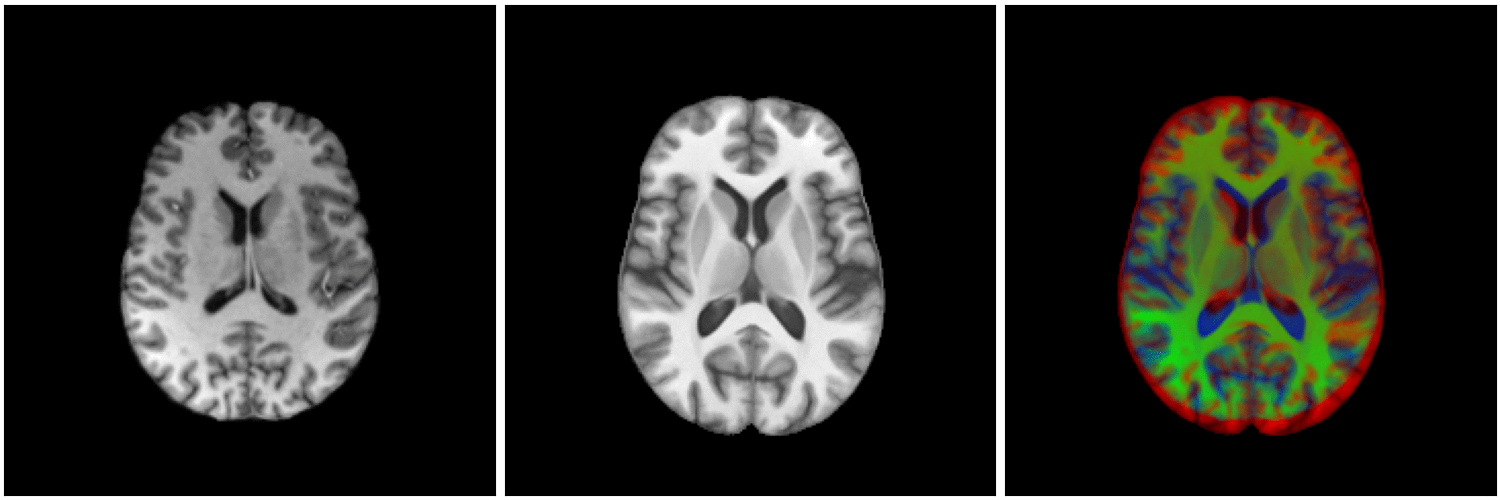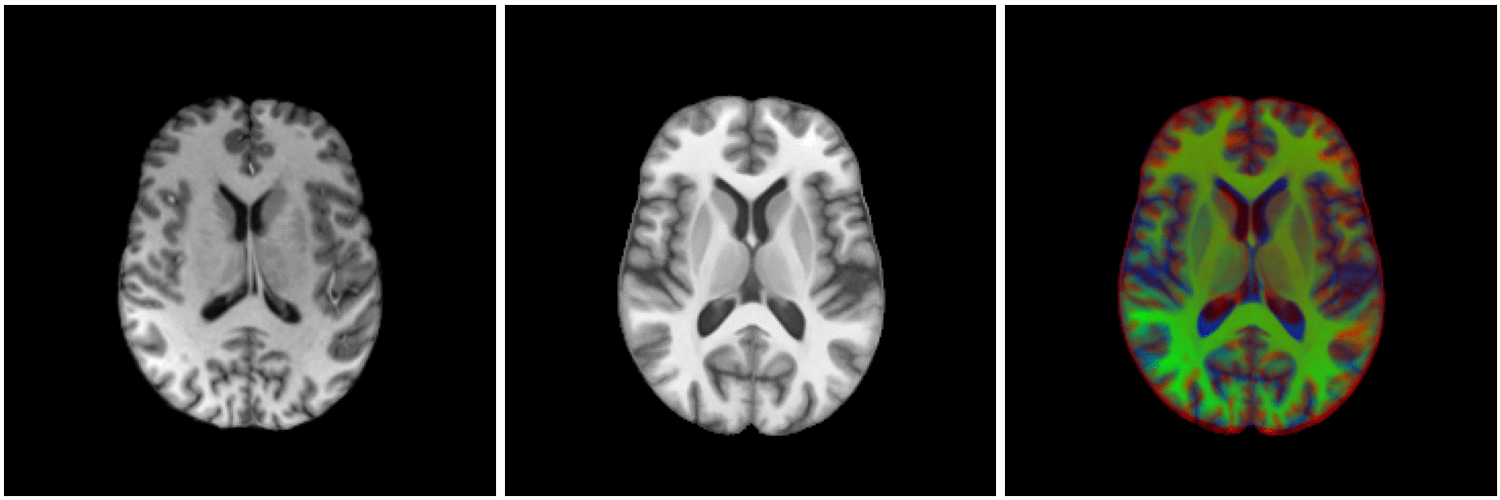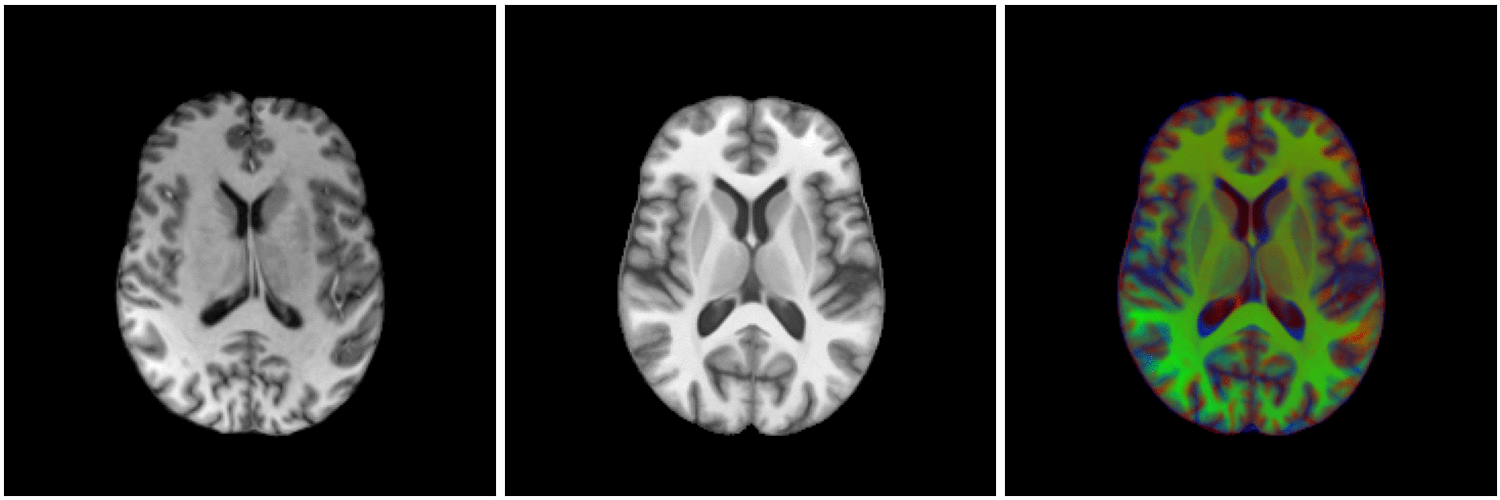
non-linear image registration: 

Image registration

temporal

Anton François - 12/02/2025

Source

Target

Automatic non-linear
 matching

LDDMM: Large Diffeomorphic Deformation Metric Mapping

With modern methods

Anton François - 12/02/2025

import demeter.metamorphosis as mt
import demeter.utils.reproducing_kernels as rk
import demeter.utils.torchbox as tb

source_name,target_name = 'm0t', 'm1c'
size = (300,300)
# go in provided example directory to get the images
S = tb.reg_open(source_name,size = size)
T = tb.reg_open(target_name,size = size)

# set a kernel operator
sigma = (32,32)
kernelOperator = rk.GaussianRKHS(sigma,kernel_reach=7)

# Peform a LDDMM
mr = mt.lddmm(S,T,0,
              cost_cst=.001,
              kernelOperator=kernelOperator,
              integration_steps=10,         #
              n_iter=15,
              grad_coef=1,
              dx_convention='square',
              hamiltonian_integration=True
)

Let \(V\) be the Reproducing Kernel Hilbert Space (RKHS) of vector fields whose kernel is \(K\). We denote \(L: V \rightarrow V^*\) the Riesz operator such that \(\|v\|^2_V = ( Lv,v)\) .

Let \(K\) be the Gaussian reproducing kernel with \[K(x,y) = \exp\left( -\frac{|x -y|^2}{2\sigma^2}\right) \cdot \mathrm{Id}_{\mathbb{R}^d}\]

V is an admissible RKHS of vector fields.

Deformation as a flow of vector field

$$\left\{\begin{array}{rl}\partial_t \varphi_t &= v_t \circ \varphi_t\\ \varphi_0&= \mathrm{Id}\end{array}\right.$$

\(v_t \in V, \forall t\in [0,1]\)

Anton François - 12/02/2025

Note : We can define other reproducing kernels as well !

Mission : level 1

- Try the different reproducing kernels available in the examples.

- What is the effect of noramalisation ?

- Hint: You can find examples here:

https://github.com/antonfrancois/Demeter_metamorphosis/tree/main/examples/2_kernels

https://antonfrancois.github.io/Demeter_metamorphosis/demeter.utils.html#module-demeter.utils.reproducing_kernels

\(G\) is a group of diffeomorphisms

The deformation defined from the ordinary differential equation:

\[\partial_t \varphi_t = v_t \circ \varphi_t; \quad \varphi_0 = \mathrm{Id}\]

with \(v_t \in V,\forall t\in [0,1]\),  is a diffeomorphism. We note \(\varphi^v \in G\) such a diffeomorphism.

\(G\) := Space of Deformations

Deformation as a flow of vector field

Anton François - 12/02/2025

\[\partial_t \varphi_t = v_t \circ \varphi_t; \quad \varphi_0 = \mathrm{Id}\]

Image transport (advection):  \[\partial_t I_t = v_t \cdot \nabla I_t \]

Deformed image

\(I_t = I_0 \circ (\varphi^v)^{-1}\)

The deformation acts on images.

Geodesic := Shortest path for the exact matching:

\[\mathrm{inf}_v \int_0^1 \|v_t\|_V^2 dt\]

Anton François - 12/02/2025

Missions: (level 1)

- Apply the deformation \(\varphi = \varphi_{0,1}\) to an image.

- Apply the inverse deformation \(\varphi^{-1}\), what happens?

- Try to apply the deformation of the first half only (i.e.: \(\varphi_{0,\frac{1}{2}}\))

import demeter.utils.torchbox as tb

mr = ... # a given Metamorphic optimisator
image = ... # open an image

# You can use the following functions and methods:
mr.mp.get_deformation()  

mr.mp.get_deformator()

tb.imgDeform(image, deformation, dx_convention = mr.dx_convention)
# Good luck !

$$\varphi_{t_1,t_2} = \mathrm{Id} + \int_{t_1}^{t_2} v_s \circ \varphi_s ds, v_s \in V$$

\[\partial_t \varphi_t = v_t \circ \varphi_t; \quad \varphi_0 = \mathrm{Id}\]

Image transport (advection):  \[\partial_t I_t = v_t \cdot \nabla I_t \]

Deformed image

\(I_t = I_0 \circ (\varphi^v)^{-1}\)

The deformation acts on images.

Geodesic := Shortest path for the exact matching:

\[\mathrm{inf}_v \int_0^1 \|v_t\|_V^2 dt\]

Distance between two images

$$d(I,J) = \mathrm{min}_{v}  \frac12 \int_0 ^1 \|v_t \|_V^2dt,$$

$$\text{s.t. }I_0 = I;  I_1 = \int_0^1 v_t \cdot\nabla I_t dt = J$$

Anton François - 12/02/2025

LDDMM can reach only images with same topology

Metamorphosis deforms images and adds intensity.

Making the registration of images B and C possible.

\[\partial_t I_t = \sqrt{\rho}v_t \cdot \nabla I_t\]

\[+ \sqrt{1 - \rho} z_t\]

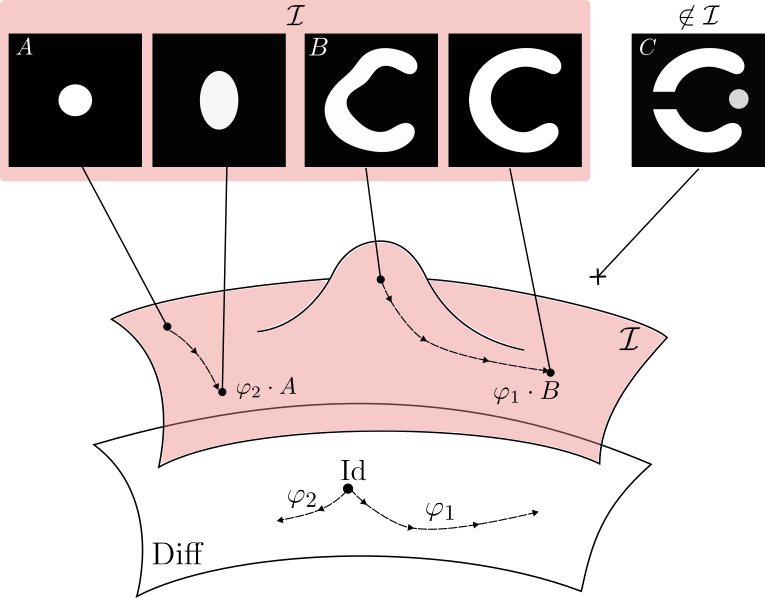
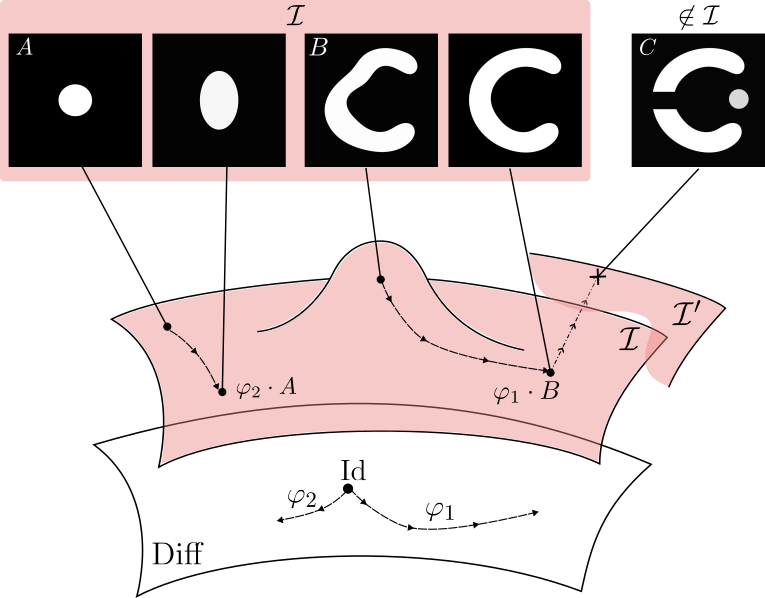
Topology and appearances variations

Anton François - 12/02/2025

A first Example

Metamorphosis

Source

Target

LDDMM

Anton François - 12/02/2025

import demeter.metamorphosis as mt
import demeter.utils.reproducing_kernels as rk
import demeter.utils.torchbox as tb

source_name,target_name = 'm0t', 'm1c'
size = (300,300)
# go in provided example directory to get the images
S = tb.reg_open(source_name,size = size)
T = tb.reg_open(target_name,size = size)

# set a kernel operator
sigma = (32,32)
kernelOperator = rk.GaussianRKHS(sigma,kernel_reach=7)

rho = .1     # amount of deformation vs intensity changes
mr = mt.metamorphosis(S,T,0,
          rho,
          cost_cst=.001,
          kernelOperator=kernelOperator,
          integration_steps=10,
          n_iter=15,
          grad_coef=1,
          dx_convention='square',
          hamiltonian_integration=True
)

Add link example

Implementation

details

Metamorphosis

A Metamorphosis on \(\mathcal I\) is a pair of curves \((\varphi_t, \psi_t)\), respectively on \(G\) and \(\mathcal I\), with \(\varphi_0 = \mathrm{Id}\).

\(G\) := Space of Deformations

\(\mathcal I\) := Space of images

\(\psi_t\) is the intensity changes evolution part: \(I_t = \psi_t \circ (\varphi_t)^{-1}\)

Anton François - 12/02/2025

Strategy overview

\(G\) := Space of Deformations

\(\mathcal I\) := Space of images

How to register in practice?

  1. Determine the geodesic expression by solving an exact-matching problem
  2. Relax the problem with inexact matching. Optimize through geodesic shooting.

Anton François - 12/02/2025

Exact matching formulation.

$$\left\{\begin{array}{rl} v &= - \sqrt{ \rho } K_{V} (p \nabla I)\\          \dot{p} &= -\sqrt{ \rho } \nabla \cdot (pv) \\  z &= \sqrt{ 1 - \rho } p \\  \dot{I} &=  - \sqrt{ \rho } v_{t} \cdot\nabla I_{t} + \sqrt{ 1-\rho } z.\end{array}\right. $$

Advection equation with source
Continuity equation

Given the image evolution model 

\[\dot I_t = - \sqrt{\rho}v_t \cdot \nabla I_t + \sqrt{1 - \rho} z_t\]

and the Hamiltonian :

$$H(I,p,v,z) = - (p |\dot{ I}) - \frac{1}{2} \|v\|^2_{V} - \frac{1}{2}(z,z)_{2}. $$
we get the optimal trajectory as a geodesic of the form:

 

[Trouvé & Younes, 2005]

Anton François - 12/02/2025

We minimize this cost :
$$ H_\mathrm M (I,v) = \frac1 2 \left\| I_1 - T \right\|_2^2 + \frac \lambda 2\int_0^1 \|v_t\|_V^2 + \|z_t\|_{L_2}^2  dt $$

 

$$ \Leftrightarrow H_\mathrm M (p_0) = \frac1 2 \left\| I_1 - T \right\|_2^2 + \frac \lambda 2\left( \|z_0\nabla I_0\|_V^2 +  \|z_0\|_{L_2}^2\right)   $$

\(v_0 = - \sqrt \rho K\star (z_0 \nabla I_0) \)

\(\|v_0\|_V+  \|z_0\|_{L^2} = \|v_t\|_V + \|z_t\|_{L^2} ,\forall t\in [0,1]\)

Metamorphosis Optimisation

via Geodesic shooting

Anton François - 12/02/2025

\[\partial_t I_t = -\sqrt{\rho}v_t \cdot \nabla I_t\]

\[+ \sqrt{1 - \rho} z_t\]

Metamorphosis Optimisation

via Geodesic shooting

We minimize the inexact matching cost :
$$ H_\mathrm M (I,v) = \frac1 2 \left\| I_1 - T \right\|_2^2 + \frac \lambda 2\int_0^1 \|v_t\|_V^2 + \|z_t\|_{L_2}^2  dt $$

 

Geodesic Integration

\(p_0\)

\(I_1\)

Step 1:

Step 2:

We iterate over two steps:

\(\nabla H_M\) and adjoint equations computed

with                     auto differentiation.

Anton François - 12/02/2025

$$\left\{\begin{array}{rl} v &= - \sqrt{ \rho } K_{V} (p \nabla I)\\          \dot{p} &= -\sqrt{ \rho } \nabla \cdot (pv) \\  z &= \sqrt{ 1 - \rho } p \\  \dot{I} &=  - \sqrt{ \rho } v_{t} \cdot\nabla I_{t} + \sqrt{ 1-\rho } z.\end{array}\right. $$

A more detailed explanation of the interaction between the integrator and the optimizer

https://antonfrancois.github.io/Demeter_metamorphosis/advanced_users.html

Using semi-Lagrangian integration schemes

[Durran 2013; Efremov et al., 2014; François 2021]

Lagrangian Formulation

$$x'(t) = v(t,x)$$

Lagrangian scheme

Not suitable for images

Eulerian scheme

\(I_{t+\delta_t} = I_t - \delta_t(v_t \times\nabla I_t)\)

Eulerian Formulation

$$\partial_t I(t,x) = - v(t,x) \cdot \nabla I(t,x)$$

Integration of the geodesics equations

Anton François - 04/06/2024

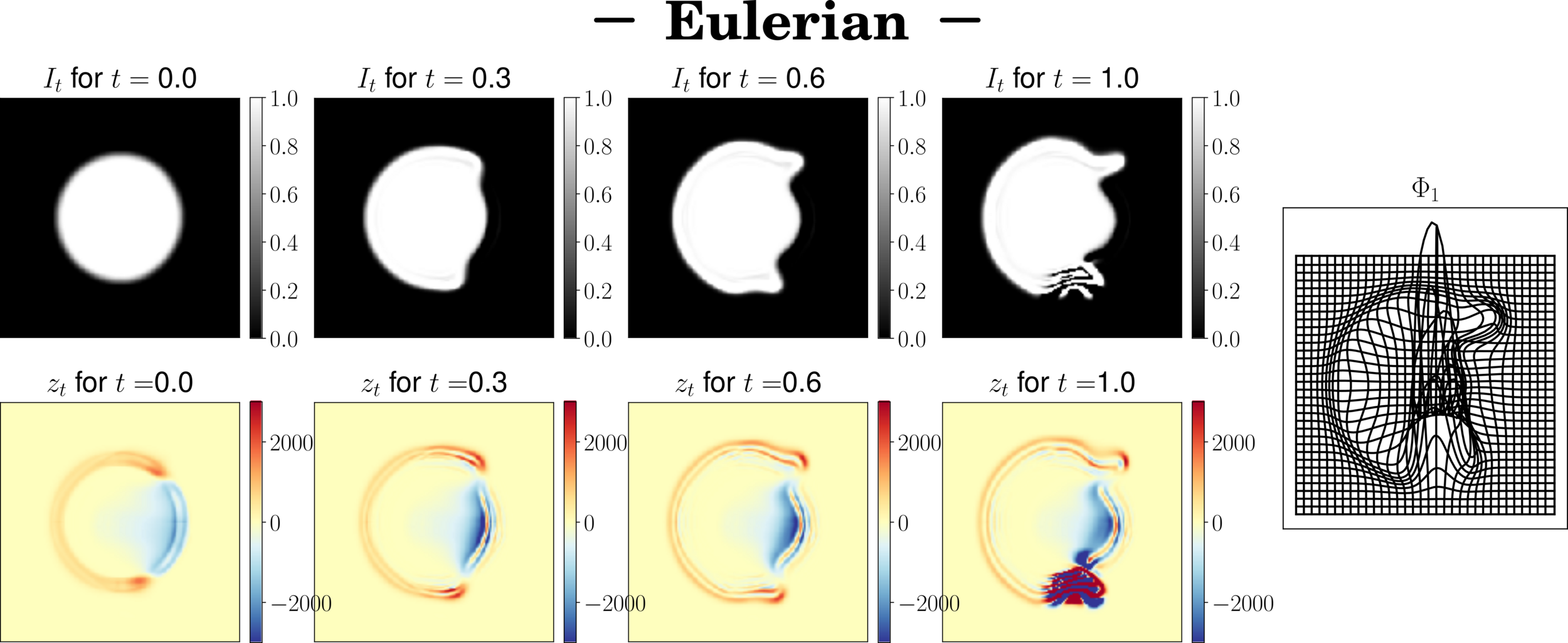
Field aberations

We have to augment the number of time steps -> slow

Schemes stability

Semi-Lagrangian scheme principle

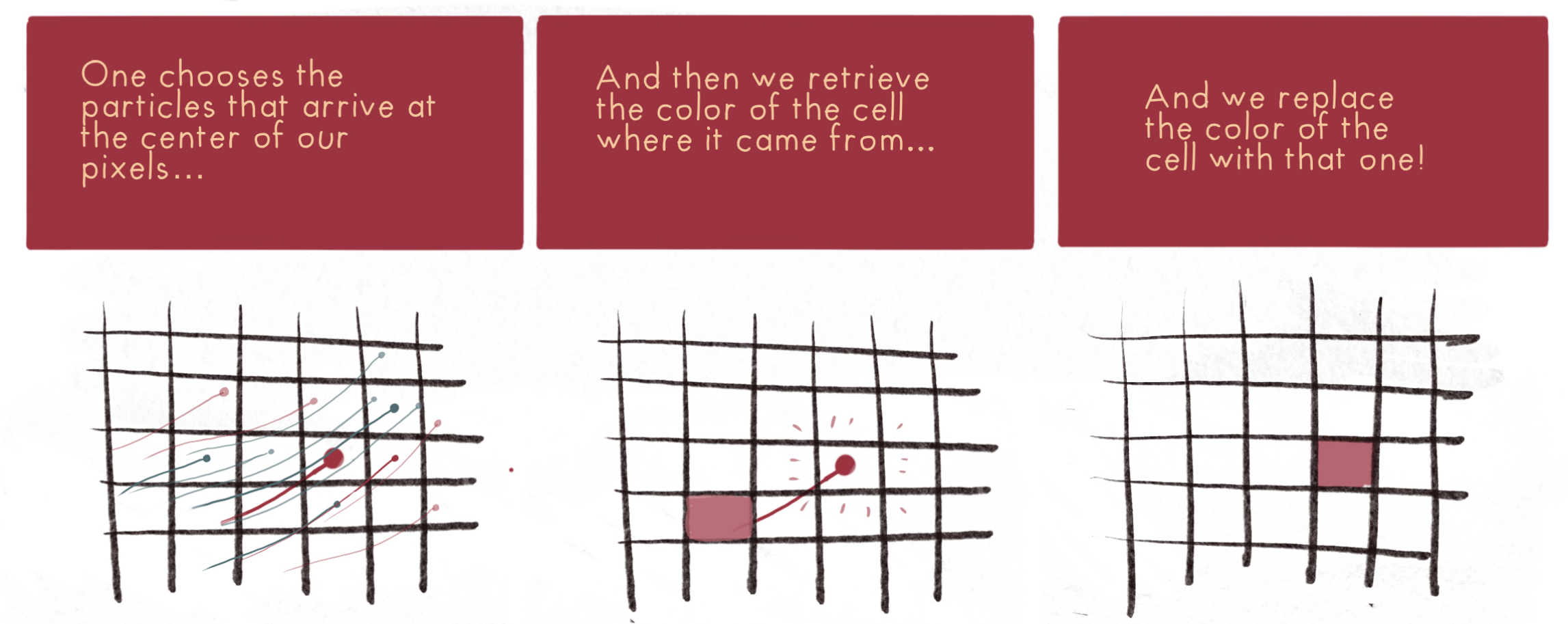
\(\partial_t I_t = v_t \cdot \nabla I_t + \mu z_t\)

Semi-Lagrangian scheme

\(I_{t+\delta_t} = \mathrm{Interp}(I_t,\varphi^{v_t}) + \delta_t \mu z_t\)

Anton François - 04/06/2024

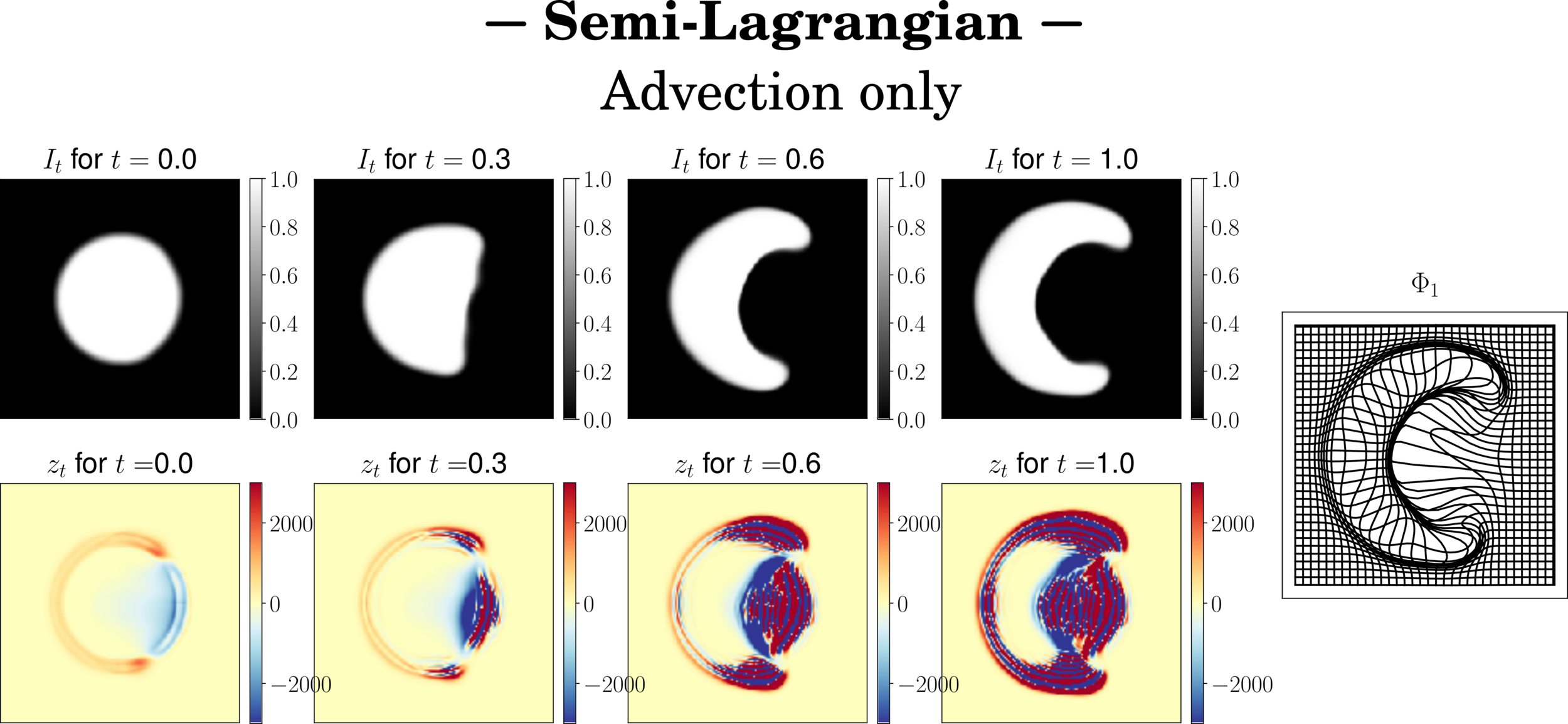
Schemes stability

Image integration more stable

residual instabilities

Anton François - 04/06/2024

Schemes stability

Stable image

 Stable residual

Semi-Lagrangian scheme on residual

\(z_{t+\delta_t} = \mathrm{Interp}(z_t,\varphi^{v_t}) - \delta_t  z_t \mathrm{div}(v_t)\)

\(\partial_t z_t = - \mathrm{div} (z_t v_t)\)

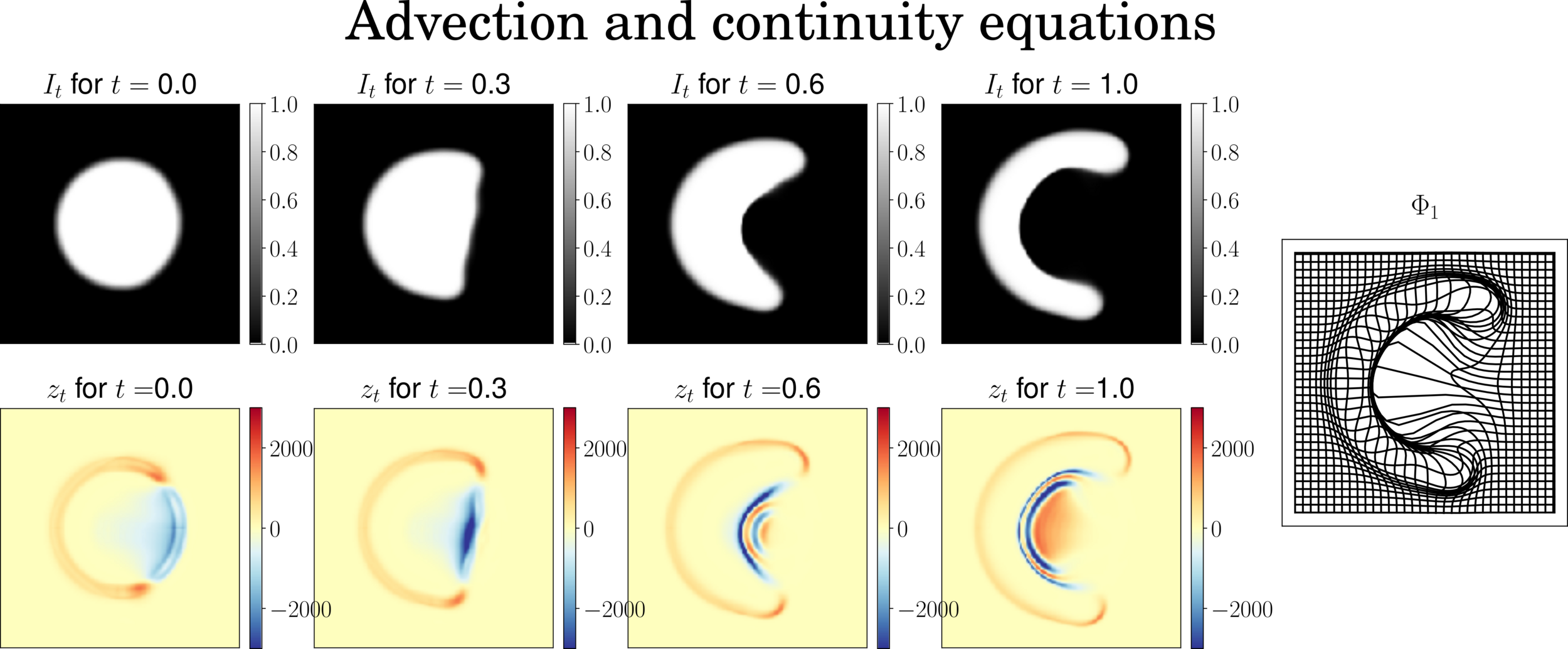
- Full semi-Lagrangian -

Anton François - 04/06/2024

Problem solved ?

Metamorphosis

Source

Target

LDDMM

$$\rho = 0.7$$

$$\rho = 0$$

$$\rho = 1$$

Anton François - 12/02/2025

$$\dot{I_{t}}= - \sqrt{ \rho } v_{t} \cdot \nabla I_{t} + \sqrt{ 1-\rho } z_{t}.$$

mr.plot()

Bad registration example

mr.plot_deform()

Deformation

Source

Target

Only Deformed image

Only Deformed image

compared with target

Bad registration example

mr.mp.plot()

Integration plot:

From left to right: Image, residuals,  deformation.

Bad registration example

Weighted Metamorphosis

Just replacing \(\rho\) with a mask \(M_t(x): \Omega \times [0,1] \mapsto [0,1]\)

$$\dot{I_{t}}= - \sqrt{ M_{t} } v_{t} \cdot \nabla I_{t} + \sqrt{ 1-M_{t} } z_{t}.$$

We model the image evolution

and take the same Hamiltonian

$$H(I,p,v,z) = - (p |\dot{ I}) - \frac{1}{2} (Lv|v)_{2} - \frac{1}{2}(z,z)_{2}$$

and obtain the geodesic équations:

$$\left\{\begin{array}{rl} v_t &= - \sqrt{ M_t } K_{V} (p_t \nabla I_t)\\ \dot{p_t} &= -\sqrt{ M_t } \nabla \cdot (p_t v_t) \\   z_t &= \sqrt{ 1 - M_t } p_t \\         \dot{I_t} &=  - \sqrt{ M_t } v_{t} \cdot \nabla I_{t} + \sqrt{ 1-M } z_t.    \end{array} \right. $$

\(\sqrt{M_t}\)

\(\sqrt{M_t}\)

\(\sqrt{M_t}\)

\(\sqrt{M_t}\)

\(\sqrt{1- M_t}\)

\(\sqrt{1- M_t}\)

\(\sqrt{1- M_t}\)

Anton François - 12/02/2025

Mission: (level 3)

Register the best you can theses two images:

# you might need the following functions:
# 
import demeter.metamorphosis as mt
import demeter.utils.torchbox as tb

tb.make_ball_at_shape_center  

mt.lddmm
mt.weighted_metamorphosis
(names 23 and 24)

You can complete the example at :https://antonfrancois.github.io/Demeter_metamorphosis/auto_examples/1_registration/toyExample_weightedMetamorphosis.html

Try to reproduce this result:

Constrained Metamorphosis

$$H(I,p,v,z) = -(p |\dot{ I}) - \frac{1}{2} (Lv|v)_{2} - \frac{1}{2}|z|_{2} $$

  • \(M_t\) : Mask -  Amount of deformation vs photometric changes.

  •  \(w_t\) : Field - guide the deformation.

  • \(Q_t\) : Mask - Where to follow \(w_t\)

$$\dot{I_{t}}= - \sqrt{ M_{t} } v_{t} \cdot \nabla I_{t} + \sqrt{ 1-M_{t} } z_{t}.$$

We set the image evolution

and the Hamiltionian

$$- \langle v,Qw\rangle_{2}.$$

we get the geodesic equation:

$$\left\{\begin{array}{rl} v_{t} &= - K_{V} (\sqrt{ M_{t} } p_{t} \nabla I_{t} + Q_{t} w_{t})\\         \dot{p_{t}} &= -\sqrt{ M_t } \nabla \cdot (p_{t}v_{t}) \\         z_{t} &= \sqrt{ 1 - M_t } p_{t} \\         \dot{I_{t}} &=  - \sqrt{ M_t } v_{t} \cdot \nabla I_{t} + \sqrt{ 1-M_t } z_{t}.    \end{array}\right.$$

\(Q_tw_t\)

Anton François - 12/02/2025

Mission: (level Expert) Reproduce this registration task:

Image (\(I_t\))

Residuals (\(z_t\))

Deformation (\(\varphi_t\))

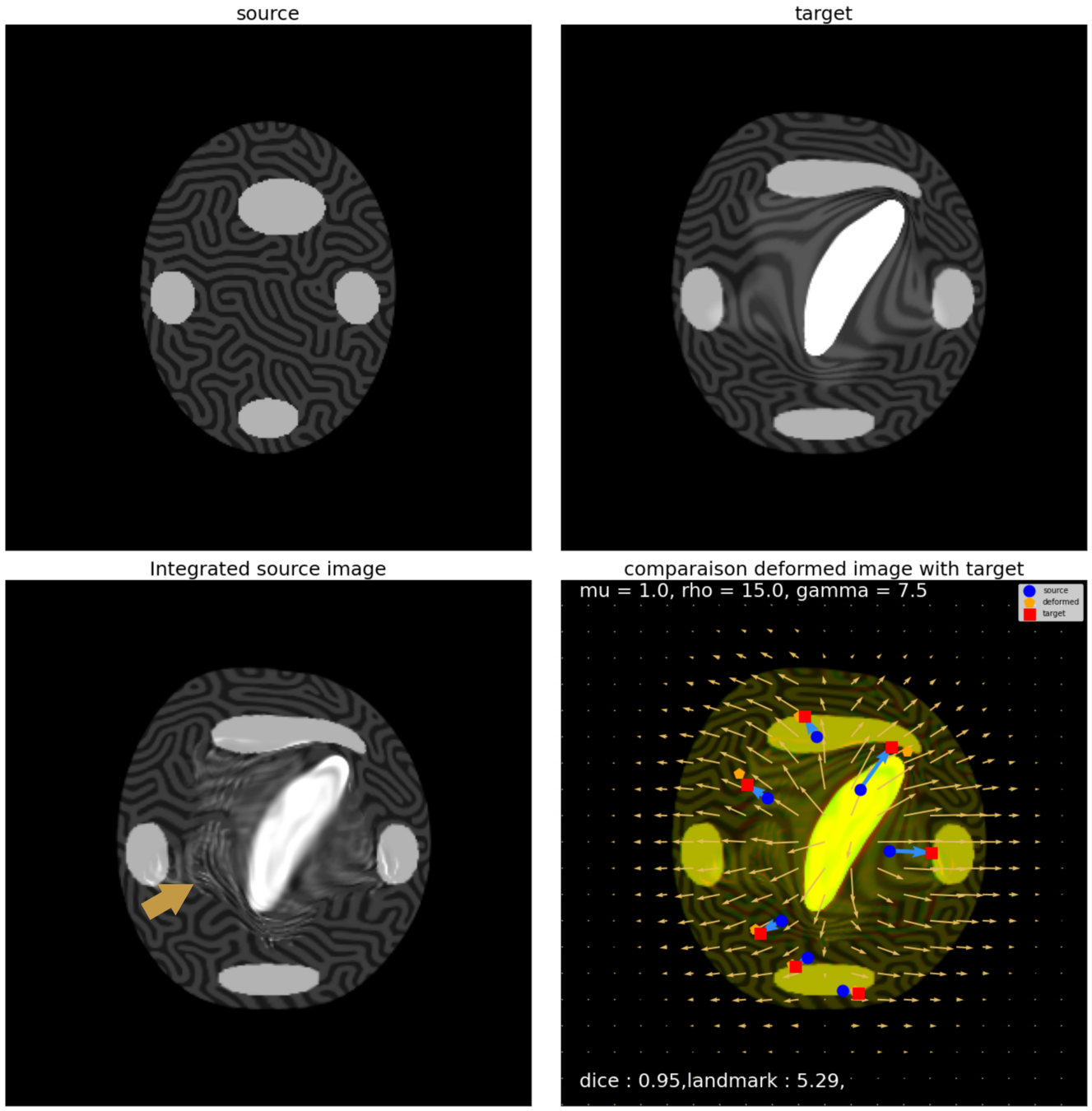
Source:

Target:

Complete the example: https://antonfrancois.github.io/Demeter_metamorphosis/auto_examples/1_registration/toyExample_weightedMetamorphosis.html

Thank you!

Tutorial Demeter

By Anton FRANCOIS

Made with Slides.com

Tutorial Demeter

  • 117

More from Anton FRANCOIS