Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
Inscription au TD sur l'ENT, mot de passe:
5
6
Chapitres >>
Sondage en direct: https://www.wooclap.com/STAT2024
ce diaporama accessible à l'adresse: https://slides.com/archeomatic/statl2
ou en Live: https://slides.com/archeomatic/statl2/live





Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
Statistiques
pour
statophobes
Une introduction au monde des tests statistiques
à l'intention des étudiants
qui n'y entravent que pouic
et qui détestent les maths par dessus le marché
Denis Poinsot
2004
Pour citer ce document :
D. Poinsot, 2004. Statistiques pour statophobes. [en ligne : http://perso.univ-rennes1.fr/denis.poinsot]


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.0
Chapitre 1- Organisation et représentation graphique des données
Calendrier 2026 - groupes du Mardi
Amélie DEHECQ
G1 = Groupe Archeo4 et Géo3 : 10h30 - 12h30
G2 = Groupe Archeo5 et Socio 2 : 13h30 - 15h30
13 janvier (G1 et G2)
20 janvier (G1 et G2)
27 janvier (G1 et G2)
3 février (G1 et G2)
17 février (G1 et G2)
3 mars (CC1 : 1h15,
TD : 45 min / G1 et G2)
10 mars (G1 et G2)
24 mars (G1 et G2)
31 mars (G1 et G2)
7 avril (G1 et G2 )
Inscription au TD sur l'ENT : A.Dehecq – MO44-EP1:TD Statistiques pour historiens

17 mars (G1 et G2)
14 avril (G1 et G2 = CC2 - 2h )


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.0
Chapitre 1- Organisation et représentation graphique des données
Calendrier 2026 - groupes du Vendredi
Sylvain BADEY
G3 = Groupe Geo6 : 14h30 - 16h30
G4 = Groupe RenfDisc7 et RenfDisc8? : 16h30 - 18h30
16 janvier (G3 et G4)
23 janvier (G3 et G4)
30 janvier (G3 et G4)
6 février (G3 et G4)
13 février (G3 et G4)
6 mars (G3 et G4) CC1
13 mars (G3 et G4)
27 mars (G3 et G4)
3 avril (G3 et G4)
10 avril (G3 et G4)
Inscription au TD sur l'ENT : S.Badey
– MO44-EP1:TD Statistiques pour historiens

20 mars (G3 et G4)
1 séance à caler CC2


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.0
Chapitre 1- Organisation et représentation graphique des données
Chapitre 1- Organisation et représentation graphique des données


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.1
Chapitre 1- Organisation et représentation graphique des données
1-1 Statistiques et Sciences humaines
Les Statistiques
Ce sont les données chiffrées (moyennes, pourcentages, indices de toute sorte) que l'on rencontre dans tous les domaines.
La statistique
C'est la discipline qui a pour objet les méthodes qui permettent d'analyser les données statistiques.
C'est une famille de techniques mathématiques qui permettent de produire, de traiter et d’interpréter des ensembles de données de manière objective et reproductible.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.2
Chapitre 1- Organisation et représentation graphique des données
Monde, dès l'antiquité:
1-2 Exemples de données statistiques
- Sources epigraphiques:
- tablettes sumériennes (3500 BC)
- le code Hammourabi (2000 BC) qui contient 285 lois.
- comptes de constructions
- recensements (census romain)
- etc.



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.2
Chapitre 1- Organisation et représentation graphique des données
France:
1-2 Exemples de données statistiques
- registres paroissiaux (1539-1792)
- registres d'état civil (>1792)
- dénombrements
- recensements
- registres matricules militaires (>1867)
- La Statistique Générale de France (>1833)
ressources:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.2
Chapitre 1- Organisation et représentation graphique des données
Séries régionales:
- sources fiscales et/ou à caractère économique
- rôles d'imposition
- censiers
- terriers
- comptabilités
- inventaires après décès
- livres de familles
- mercuriales
ressources:
1-2 Exemples de données statistiques


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
1-3 Vocabulaire élementaire de statistiques
1-3-1 population et individu
- population (ou population statistique) : ensemble concerné par une étude statistique. On parle aussi de champ de l'étude.
- individu (ou unité statistique) : on désigne ainsi tout élément de la population considérée. C’est une entité élémentaire sur laquelle on va mesurer ou observer des phénomènes.
- échantillon : dans une étude statistique, il est fréquent que l’on n’observe pas la population tout entière. On appelle donc échantillon le sous-ensemble de la population sur lequel sont effectivement réalisées les observations.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
- variable (ou caractère) statistique : c’est une caractéristique (âge, salaire, sexe...), définie sur la population et observée sur l'échantillon. C’est une propriété commune à tous les individus d’une population.
- modalité : c’est une caractéristique (âge, salaire, sexe...), définie sur la population et observée sur l'échantillon. C’est la valeur ou la situation prise par une variable pour un individu.
Les modalités sont :
Incompatibles entres elles → pour une variable , un individu ne peut enregistrer qu’une modalité .
Exhaustives → tous les individus d’une population possèdent une modalité pour la variable (sinon on parle de valeur manquante ou nodata)
!
1-3-2 variable et modalités


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Les données sont en général présentées sous forme de tableau élémentaire (individus en lignes et variables en colonnes) et stockées dans un fichier informatique.
- données (statistiques) : désignent l’ensemble des individus observées (ceux de l'échantillon) + l’ensemble des variables considérées + les observations de ces variables sur ces individus (modalités).
0101
1010
0101
1010
0101
1010
1010
0101
1010
1-3-3 données et tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
- tableau élémentaire : C’est un tableau à double entrée où les lignes correspondent aux individus et les colonnes aux variables décrivant ces éléments.
La 1ère colonne est souvent réservée à la liste nominale des éléments sans que cela soit obligatoire.
En l’absence d’identifiant, on repère les éléments par leur ordre d’apparition (leur rang) dans le tableau: on crée une colonne avec les lignes numérotées de 1 à )
!
1-3-3 données et tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
| ID | profession |
|---|---|
| 1 | agriculteur |
| 2 | menuisier |
| 3 | agriculteur |
| 4 | agriculteur |
| 5 | marchand |
| 6 | marchand |
| 7 | agriculteur |
| 8 | militaire |
| 9 | marchand |
| 10 | militaire |
Tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
| ID | profession |
|---|---|
| 1 | agriculteur |
| 2 | menuisier |
| 3 | agriculteur |
| 4 | agriculteur |
| 5 | marchand |
| 6 | marchand |
| 7 | agriculteur |
| 8 | militaire |
| 9 | marchand |
| 10 | militaire |
la liste des
10 individus
Tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
| ID | profession |
|---|---|
| 1 | agriculteur |
| 2 | menuisier |
| 3 | agriculteur |
| 4 | agriculteur |
| 5 | marchand |
| 6 | marchand |
| 7 | agriculteur |
| 8 | militaire |
| 9 | marchand |
| 10 | militaire |
variable
la liste des
10 individus
Tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
| ID | profession |
|---|---|
| 1 | agriculteur |
| 2 | menuisier |
| 3 | agriculteur |
| 4 | agriculteur |
| 5 | marchand |
| 6 | marchand |
| 7 | agriculteur |
| 8 | militaire |
| 9 | marchand |
| 10 | militaire |
variable
les modalités
la liste des
10 individus
Tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
| ID | profession |
|---|---|
| 1 | agriculteur |
| 2 | menuisier |
| 3 | agriculteur |
| 4 | agriculteur |
| 5 | marchand |
| 6 | marchand |
| 7 | agriculteur |
| 8 | militaire |
| 9 | marchand |
| 10 | militaire |
variable
discrète
les modalités
la modalité prise
par l'individu 5 pour
la variable "profession"
la liste des
10 individus
Tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
| ID | |
|---|---|
| 1 | |
| 2 | |
| ... | ... |
| ... | ... |
| ... | ... |
| ... | ... |
| ... | ... |
| .. | ... |
la liste des
individus
variable
discrète
les modalités
Tableau élémentaire
la modalité prise
par l'individu
pour la variable


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
une variable peut être
Qualitative
Les modalités expriment l'appartenance à une catégorie.
Ex: profession d'un individu , période historique, présence/absence,...
Quantitative
Les modalités s'expriment en nombres réels.
Il est possible de les ordonner et de faire des calculs dessus.
Ex: Âge, taille d'un individu, nombre de personne dans un foyer,...
1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
une variable peut être
Qualitative
Les modalités expriment l'appartenance à une catégorie.
Ex: profession d'un individu , période historique, présence/absence,...
1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Qualitative
Ordinale
l’ordre des modalités à un sens, il possède une logique.
Ex: période chronologique, état de conservation d'un squelette,...

1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Qualitative
Nominale
l’ordre des modalités n’a pas de sens.
Les modalités ne sont pas ordonnées entre elles.
Ex: orientation de sépultures, présence/absence de carie sur une dent, de négatif dans un poteau

1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Qualitative
Binaire
Il n'y a que 2 modalités exclusives:
oui / non
vrai / faux
Ex: présence/absence de carie sur une dent,...

1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Qualitative
Ordinale
Nominale
Discrète
Les modalités sont en nombre limité.
Il y a moins de modalités que d’individus.
Ex: profession, période chronologique


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Qualitative
Ordinale
Nominale
Exhaustive
Il y a autant de modalités que d’individus.
Ex: n° d'identifiant
=> pas d’intérêt statistique !!
Discrète
Les modalités sont en nombre limité.
Il y a moins de modalités que d’individus.
Ex: profession, période chronologique


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Quantitative
Absolue
Exprime des quantités concrètes.
La somme des modalités des individus a un sens.
Ex: Âge, longueur, surface,…
1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Quantitative
Absolue
Exprime des quantités concrètes.
La somme des modalités des individus a un sens.
Ex: Âge, longueur, surface,…
Relative
Un rapport entre deux valeurs.
On peut calculer une moyenne mais la somme n’a pas de sens.
Les modalités peuvent être ordonnées.
Ex : nombre d'habitants au km²,..
1-3-4 Les types / natures des Variables


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Quantitative
Absolue
Relative
Discrète
Les modalités correspondent à un nombre fini de valeurs isolées.
Généralement des nombres entiers.
Ex: Nombre de personnes dans un foyer, Comptages de céramique,...



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Quantitative
Absolue
Relative
Continue
Les valeurs potentiellement prises par la variable sont en nombre infini.
Généralement des nombres réels (=décimaux)
Ex : les mesures (taille, longueur,etc.)



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Quantitative
Absolue
Relative
Repérable
sur une échelle d'intervalle
Chaque élément est repéré par rapport à une origine arbitraire = La valeur 0 ne signifie pas l'absence du phénomène.
Ex. : Latitude, longitude, température, altitude, ...


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
Variable Quantitative
Absolue
Relative
Repérable
sur une échelle d'intervalle
Chaque élément est repéré par rapport à une origine arbitraire = La valeur 0 ne signifie pas l'absence du phénomène.
Ex. : Latitude, longitude, température, altitude, ...
Mesurable
On peut mesurer une modalité sur une échelle numérique.
Le 0 signifie bien l'absence du phénomène
Ex. : Nombre de personnes d'un ménage, comptages de céramique,...


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.3
Chapitre 1- Organisation et représentation graphique des données
1-3-4 Les types / natures des Variables



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.4
Chapitre 1- Organisation et représentation graphique des données
1-4 Les différentes phases d'une étude statistique
1. définition du champ d'étude → population et variables étudiées
2. Collecte des renseignements
a. méthodes d'observation directe
- relevé exhaustif / recensement → population
- sondage → échantillon questionné
- choix au hasard → échantillon aléatoire simple
- choix raisonné → échantillon représentatif
b. méthodes d'observation indirecte → documents préexistants
3. Dépouillement et présentation des résultats
a. dépouillement
b. résultats → présentés sous forme de tableaux et/ou graphiques


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.4
Chapitre 1- Organisation et représentation graphique des données
1-4 Statistique descriptive vs inductive
Statistique Descriptive / exploratoire
a pour but de résumer l'information contenue dans les données de façon synthétique et efficace à l’aide d’indicateurs numériques, de tableaux et de graphiques. C'est l'objet de cette formation.
Statistique Probabiliste / Inférentielle
permet de généraliser a de grands ensembles les résultats obtenus avec des ensembles plus restreints appelés échantillons.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.4
Chapitre 1- Organisation et représentation graphique des données
1-4 Statistique descriptive vs inductive



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.4
Chapitre 1- Organisation et représentation graphique des données
1-4 Statistique descriptive vs inductive




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
1-5 Variable qualitative: présentation des données
| ID | profession |
|---|---|
| 1 | agriculteur |
| 2 | menuisier |
| 3 | agriculteur |
| 4 | agriculteur |
| 5 | marchand |
| 6 | marchand |
| 7 | agriculteur |
| 8 | militaire |
| 9 | marchand |
| 10 | militaire |
| modalité de la variable | effectif |
|---|---|
| agriculteur | 4 |
| menuisier | 1 |
| marchand | 3 |
| militaire | 2 |
| TOTAL | =10 |
tableau de dénombrement
=tri à plat
tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
1-5-1 Tableau de dénombrement
| modalité de la variable | effectif |
|---|---|
| agriculteur | 4 |
| menuisier | 1 |
| marchand | 3 |
| militaire | 2 |
| TOTAL | =10 |
Il est composé de
3 colonnes:
• La liste des modalités de la variable
• L'effectif
(= Fréquence absolue)


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
1-5-1 Tableau de dénombrement
| modalité de la variable | effectif | fréquence relative |
|---|---|---|
| agriculteur | 4 | 40% |
| menuisier | 1 | 10% |
| marchand | 3 | 30% |
| militaire | 2 | 20% |
| TOTAL | =10 | 100 |
Il est composé de
3 colonnes:
• La liste des modalités de la variable
• L'effectif
(= fréquence absolue)
• La fréquence relative
(éventuellement en %)




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
| modalité de la variable | effectif | fréquence relative |
|---|---|---|
| ... | ... | ... |
| TOTAL | 1 |
• La liste des modalités
tel que
est la première modalité repérée pour la variable
et
est la ème modalité repéré pour la variable


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
| modalité de la variable | effectif | fréquence relative |
|---|---|---|
| ... | ... | ... |
| TOTAL | 1 |
tel que
est le nombre d'individus
pour lesquels la variable
prend la modalité
et
est le nombre d'individus
pour lesquels la variable
prend la modalité
et
• L'effectif (= fréquence absolue)


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
| modalité de la variable | effectif | fréquence relative |
|---|---|---|
| ... | ... | ... |
| TOTAL | 1 |
• La fréquence relative


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
1-5 variable qualitative: représentations graphique
Diagramme en bâton / en barre
• C'est la représentation graphique normale d'un caractère discret.
• abscisse = suite ordonnée des modalités
• ordonnée = effectif ou fréquence relative
Les Barres sont:
- non-jointives
-de largeur constante

!




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
Diagramme en bâton / en barre
Importations de fromage au Canada en 2016 (in Les Echos - déc. 2017)

variable qualitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
• Représentation consistant à découper une barre (représentant 100% de l’effectif) en segments dont la longueur est proportionnelle à l’effectif de chaque modalité.
• Particulièrement intéressante dans le cas des caractères où il existe un ordre entre les modalités.
Diagramme en barres empilées / à bandes subdivisées


variable qualitative discrète:




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
Diagramme circulaire ou camembert
!


• Permet de visualiser des parts relatives, dans des surfaces ou secteurs de cercle, que l’on différencie par des couleurs ou des trames différentes.
• Chaque secteur correspond à une modalité.
Représentation équivalente au diagramme en bâtons mais moins performantes sur le plan visuel...
variable qualitative discrète:



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données

Diagramme circulaire
variable qualitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données


Diagramme circulaire
variable qualitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données

tranches de taille identiques
tranches de
taille
identiques

Diagramme circulaire
variable qualitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
Diagramme circulaire
variable qualitative discrète:
Importations de fromage au Canada en 2016 (in Les Echos - déc. 2017)



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.5
Chapitre 1- Organisation et représentation graphique des données
Diagramme en étoile / de Kiviat
variable qualitative discrète:
• 1 modalité = 1 axe.
• Représentation adaptée aux caractères cycliques
et pour comparer 2 séries
avec les mêmes modalités et des valeurs proches.
les écarts d’effectifs ne doivent pas être trop importants!
!





Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
1-6-1 Variable quantitative discrète: présentation des données
une variable quantitative discrète:
- c'est une variable quantitative.
- elle ne prend que des valeurs entières (plus rarement décimales).
- Le nombre de valeurs distinctes est habituellement assez faible (sauf exception, moins d’une vingtaine).
exemple: le nombre d’enfants dans une population de familles, le nombre d’années d’études après le bac dans une population d’étudiants.
Note: la moyenne (et l'écart-type) ont un sens.
!


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| ID | nb_enfant |
|---|---|
| 1 | 3 |
| 2 | 1 |
| 3 | 3 |
| 4 | 4 |
| 5 | 3 |
| 6 | 4 |
| 7 | 2 |
| 8 | 2 |
| 9 | 3 |
| 10 | 4 |
| modalités de la variable | effectif |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 4 |
| 4 | 3 |
| TOTAL | =10 |
tableau de dénombrement
tableau délémentaire
variable quantitative discrète:
→ tableau de distribution statistiques


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| modalités de la variable | effectif | fréquence relative |
||
|---|---|---|---|---|
| 1 | 1 | 10% | ||
| 2 | 2 | 20% | ||
| 3 | 4 | 40% | ||
| 4 | 3 | 30% | ||
| TOTAL | =10 | 100% |
tableau de distribution statistiques


variable quantitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| modalités de la variable | effectif | fréquence relative |
effectif cumulé |
|
|---|---|---|---|---|
| 1 | 1 | 10% | 1 | |
| 2 | 2 | 20% | 3 | |
| 3 | 4 | 40% | 7 | |
| 4 | 3 | 30% | 10 | |
| TOTAL | =10 | 100% |
tableau de distribution statistiques


variable quantitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| modalités de la variable | effectif | fréquence relative |
effectif cumulé |
fréquence cumulé |
|---|---|---|---|---|
| 1 | 1 | 10% | 1 | 10% |
| 2 | 2 | 20% | 3 | 30% |
| 3 | 4 | 40% | 7 | 70% |
| 4 | 3 | 30% | 10 | 100% |
| TOTAL | =10 | 100% |
tableau de distribution statistiques


variable quantitative discrète:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
1-6-1 Variable quantitative discrète: représentation graphique
comme pour une variable qualitative discrète ordonnée
- l'ordre des modalités est essentiel
- ajouter l'effectif total
- + éventuellement la moyenne et l'écart-type


1
2
3
4
répartition du nombre
d'enfants par individu


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
1-6-2 Variable quantitative continue: présentation des données
une variable quantitative continue comprend potentiellement une infinité de valeurs/modalités
→ on regroupe les valeurs dans des classes de valeurs
= discrétisation (passer d'une variable continue à une variable discrète)
Voir exemple des empereurs (parties a. et b. du cours) puis celle de la taille (partie c. du cours, voir diapo suivante)


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| 10 | 173 |
| variable partitionnée classe | effectif |
|---|---|
| [160-170[ | 3 |
| [170-180[ | 4 |
| [180-190] | 3 |
| TOTAL | =10 |
tableau de distribution
statistiques
tableau élémentaire
variable quantitative continue:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| taille (classes) |
amplitude de classe |
centre de classe | effectif | fréquence relative |
|---|---|---|---|---|
| [160-170[ | 10 | 165 | 3 | 30% |
| [170-180[ | 10 | 175 | 4 | 40% |
| [180-190] | 10 | 185 | 3 | 30% |
| TOTAL | =10 | 100% |
tableau de distribution statistiques


variable quantitative continue:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
1-6-2 Variable quantitative continue: représentation graphique: l'Histogramme

classes d'amplitudes égales


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
Variable quantitative continue: Histogramme

←variable continue = rectangles contigus→

la surface des rectangles
est proportionnelle à l'effectif !



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
variable quantitative continue: construction du polygone des effectifs d'après l'Histogramme



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
variable quantitative continue: construction du polygone des effectifs d'après l'Histogramme



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| durée règne (classes) |
amplitude de classe |
effectif | fréquence relative |
|---|---|---|---|
| [0-5[ | 5 | 11 | 0.42 |
| [5-10[ | 5 | 2 | 0.08 |
| [10-20] | 10 | 9 | 0.35 |
| [20-41] | 21 | 4 | 0.15 |
| TOTAL | = 26 | 1 |
tableau de distribution statistiques - amplitudes inégales


variable quantitative continue:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
Histogramme avec
classes d'amplitudes inégales
J'ai dit: des classes d'amplitudes
INÉGALES !




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
Histogramme avec
classes d'amplitudes inégales
J'ai dit: des aires proportionnelles à l'effectif !




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
| durée règne (classes) |
amplitude de classe |
effectif | fréquence relative |
densité de fréquence |
|---|---|---|---|---|
| [0-5[ | 5 | 11 | 0.42 | 0.084 |
| [5-10[ | 5 | 2 | 0.08 | 0.016 |
| [10-20] | 10 | 9 | 0.35 | 0.035 |
| [20-41] | 21 | 4 | 0.15 | 0.007 |
| TOTAL | = 26 | 1 |
tableau de distribution statistiques - amplitudes inégales


variable quantitative continue:


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
Histogramme avec
classes d'amplitudes inégales




Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
Histogramme avec
classes d'amplitudes inégales


la somme des aires des rectangles est
0,42 +0,8+ 0,35 + 0,15 = 1
classes d'amplitudes inégales


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
1-6-2 Variable quantitative continue: représentation graphique:
la courbe cumulative croissante

sylvain.badey@univ-tours.fr
| durée règne (classes) |
effectif | fréquence relative |
fréquence cumulée |
|---|---|---|---|
| [0-5[ | 11 | 0.42 | 0.42 |
| [5-10[ | 2 | 0.08 | 0.5 |
| [10-20] | 9 | 0.35 | 0.85 |
| [20-41] | 4 | 0.15 | 1 |
| = 26 | 1 |


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
la courbe cumulative croissante

sylvain.badey@univ-tours.fr

Bornes


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
la courbe cumulative croissante

sylvain.badey@univ-tours.fr

Bornes
50 % des empereurs
...


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
1.6
Chapitre 1- Organisation et représentation graphique des données
la courbe cumulative croissante

sylvain.badey@univ-tours.fr

Bornes
50 % des empereurs
...
ont régné moins de 10 ans


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.0
Chapitre 2 - Caractéristiques de tendance centrale
Chapitre 2- Caractéristiques de tendance centrale et de dispersion
2-1 Caractéristiques de tendance centrale
2-2 Caractéristiques de dispersion
2-1 Caractéristiques de tendance centrale
2-2-1-1 Étendue
2-2-1-2 Écart Interquartile
2-2-1-3 Écart arithmétique (ou écart absolu moyen)
2-2-2-2 Écart-type
2-2-2-1 Variance


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.0
Chapitre 2 - Caractéristiques de tendance centrale
Chapitre 2- Caractéristiques de tendance centrale et de dispersion


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.0
Chapitre 3 - Caractéristiques de dispersion
Chapitre 2-1- Caractéristiques de tendance centrale


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.1
Chapitre 2- Caractéristiques de tendance centrale
2-1-1 Mode(s)
C'est la valeur la plus souvent observée dans un ensemble de données.
| taille |
|---|
| 160 |
| 175 |
| 162 |
| 183 |
| 165 |
| 189 |
| 185 |
| 173 |
| 179 |
| 173 |
| taille |
|---|
| 160 |
| 162 |
| 165 |
| 173 |
| 173 |
| 175 |
| 179 |
| 183 |
| 185 |
| 189 |
tri
tableau élémentaire


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.1
Chapitre 2- Caractéristiques de tendance centrale
2-1-1 Mode(s)
la classe modale est la classe avec l'effectif le plus important (amplitudes égales) ou de densité maximale (amplitudes inégales).
| variable partitionnée classe | effectif |
|---|---|
| [160-170[ | 3 |
| [170-180[ | 4 |
| [180-190] | 3 |
| TOTAL | =10 |
tableau de distribution
statistiques


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.1
Chapitre 2- Caractéristiques de tendance centrale
2-1-1 Mode(s)
• Il peut ne pas avoir de mode, un seul (distribution unimodale) ou plusieurs (distribution bi/pluri-modale).
• Si la variable est continue il faut la partitionner en classes (enlever des décimales) pour définir une classe modale.
C'est la valeur la plus souvent observée dans un ensemble de données.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.2
Chapitre 2- Caractéristiques de tendance centrale
2-1-2 Médiane (et quantiles)
C'est la valeur, observée ou possible, qui partage la série d'observations en deux ensembles de même effectif.
tri
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 162 |
| 3 | 165 |
| 4 | 173 |
| 5 | 175 |
| 6 | 179 |
| 7 | 183 |
| 8 | 185 |
| 9 | 189 |
4 individus ont une taille inférieure à ↓
4 individus ont une taille supérieure à ↑
Cas d'un nombre d'observations impair
Sur
= 9 individus,
Sur


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.2
Chapitre 2- Caractéristiques de tendance centrale
2-1-2 Médiane (et quantiles)
C'est la valeur, observée ou possible, qui partage la série d'observations en deux ensembles de même effectif.
tri
5 individus ont une taille inférieure à ↓
5 individus ont une taille supérieure à ↑
Cas d'un nombre d'observations pair
Sur
= 10 individus,
Sur
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| 10 | 173 |
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 162 |
| 3 | 165 |
| 4 | 173 |
| 5 | 173 |
| 6 | 175 |
| 7 | 179 |
| 8 | 183 |
| 9 | 185 |
| 10 | 189 |


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.2
Chapitre 2- Caractéristiques de tendance centrale
2-1-2 Médiane (et quantiles)
détermination graphique

50%
10ans


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.2
Chapitre 2- Caractéristiques de tendance centrale
2-1-2 Médiane (et quantiles)
C'est la valeur, observée ou possible, dans la série de données classée par ordre croissant qui partage cette série en deux parties comprenant exactement le même nombre de données de part et d'autre.
• Elle n'est pas influencée par les valeurs extrêmes ou aberrantes.
• Elle ne se prête pas aux combinaisons arithmétiques : la médiane d'une série ne peut pas être déduite des médianes des séries composantes.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.2
Chapitre 2- Caractéristiques de tendance centrale
2-1-2 Les quantiles
A l'instar de la médiane (notée ) qui divise une série en 2 ensembles de même effectifs, les Quartiles partagent une série en quatre ensembles de même effectifs
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 162 |
| 3 | 165 |
| 4 | 173 |
| 5 | 173 |
| 6 | 175 |
| 7 | 179 |
| 8 | 183 |
| 9 | 185 |
| 10 | 189 |
2,5 individus
2,5 individus
2,5 individus
2,5 individus


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.3
Chapitre 2- Caractéristiques de tendance centrale
2-1-3 Moyennes
C'est la somme de toutes les valeurs observées divisée nombre d’observations
Moyenne arithmétique
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| 10 | 173 |


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.3
Chapitre 2- Caractéristiques de tendance centrale
2-1-3 Moyennes
• Elle permet de résumer par un seul nombre la série statistique.
• Elle prend en compte toutes les valeurs de la série et elle est facile calculer.
• Elle est sensible aux valeurs extrêmes (il est parfois nécessaire de supprimer des valeurs extrêmes ou « aberrantes »)
C'est la somme de toutes les valeurs observées divisée nombre d’observations
Moyenne arithmétique


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.3
Chapitre 2- Caractéristiques de tendance centrale
C'est la somme de toutes les valeurs affectées des coefficients respectifs divisée par l'effectif total
Moyenne arithmétique pondérée
| nombre d'enfants | effectif |
|---|---|
| 1 | 9 |
| 2 | 5 |
| 3 | 5 |
| 4 | 1 |
| TOTAL | =20 |
pour une série de nombres
variable quantitative discrète: tableau de dénombrement


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
2.3
Chapitre 2- Caractéristiques de tendance centrale
C'est la somme des centres de classes affectées de leurs effectifs respectifs divisée par l'effectif total
Moyenne arithmétique
variable quantitative continue partitionnée en classes
| variable (classes) | centre de classe | effectif |
|---|---|---|
| [160-170[ | 165 | 3 |
| [170-180[ | 175 | 4 |
| [180-190] | 185 | 3 |
| TOTAL | =10 |


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.0
Chapitre 3 - Caractéristiques de dispersion
Chapitre 2-2- Caractéristiques de dispersion
2-2-1-1 Étendue
2-2-1-2 Écart Interquartile
2-2-1-3 Écart arithmétique (ou écart absolu moyen)
2-2-2-2 Écart-type
2-2-2-1 Variance


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.1
Chapitre 3 - Caractéristiques de dispersion
2-2-1 Écarts élémentaires
C'est la différence entre la valeur maximum et la valeur minimale.
Étendue
tri
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| 10 | 173 |
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 162 |
| 3 | 165 |
| 4 | 173 |
| 5 | 173 |
| 6 | 175 |
| 7 | 179 |
| 8 | 183 |
| 9 | 185 |
| 10 | 189 |


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.1
Chapitre 3 - Caractéristiques de dispersion
2-2-1 Écarts élémentaires
C'est la différence entre la valeur maximum et la valeur minimale.
Étendue
• Elle est facile à calculer
• Elle ne tient compte que des valeurs extrêmes de la série ; elle ne dépend ni du nombre, ni des valeurs intermédiaires.
• Lorsque le nombre d'individu est faible elle donne une idée appréciable de la dispersion sinon on lui préfère l'écart-type.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.1
Chapitre 3 - Caractéristiques de dispersion
2-2-1 Écarts élémentaires
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 162 |
| 3 | 165 |
| 4 | 173 |
| 5 | 173 |
| 6 | 175 |
| 7 | 179 |
| 8 | 183 |
| 9 | 185 |
| 10 | 189 |
2,5 individus
2,5 individus
2,5 individus
2,5 individus
Écart interquartile
C'est la différence entre le 3ème (dernier) et le 1er quartile.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.1
Chapitre 3 - Caractéristiques de dispersion
2-2-1 Écarts élémentaires
Écart interquartile
C'est la différence entre le 3ème (dernier) et le 1er quartile.
• Écart interquartile = Intervalle
• Il concerne 50% de la population (c'est l'équivalent de l'étendue pour les 50% de la population centrale).
• Il correspond à la "boîte" de la boîte à moustache
25% de la population
25% de la population
50% de la population


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.1
Chapitre 3 - Caractéristiques de dispersion
2-2-1 Écarts élémentaires
Écart interquartile
C'est la différence entre le 3ème (dernier) et le 1er quartile.

• Il correspond à la "boîte" de la boîte à moustache.
• Il permet de calculer les valeurs atypiques de la boîte à moustache.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.1
Chapitre 3 - Caractéristiques de dispersion
2-2-1 Écarts élémentaires
C'est la moyenne arithmétique des écarts à la moyenne.
écart arithmétique
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| 10 | 173 |
avec la moyenne


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 3 - Caractéristiques de dispersion
2-2-2 Variance et écart-type
C'est la moyenne de la somme des carrés des écarts à la moyenne
| ID | taille |
|---|---|
| 1 | 160 |
| 2 | 175 |
| 3 | 162 |
| 4 | 183 |
| 5 | 165 |
| 6 | 189 |
| 7 | 185 |
| 8 | 173 |
| 9 | 179 |
| 10 | 173 |


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 3 - Caractéristiques de dispersion
2-2-2 Variance et écart-type
autre formule de calcul de la variance si la variable quantitative est pondérée par un coefficient (plus facile à la calculatrice)
| ID | taille | nb |
|---|---|---|
| 1 | 160 | 1 |
| 2 | 175 | 1 |
| 3 | 162 | 1 |
| 4 | 183 | 1 |
| 5 | 165 | 1 |
| 6 | 189 | 1 |
| 7 | 185 | 1 |
| 8 | 173 | 2 |
| 9 | 179 | 1 |



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 3 - Caractéristiques de dispersion
2-2-2 Variance et écart-type
C'est la moyenne de la somme des carrés des écarts à la moyenne
• Elle est appelée aussi variance empirique.
• Elle ne s'exprime pas dans la même unité que celle de la variable
=> On lui préfère l'écart-type
• Si on étudie un échantillon on enlève 1 à l'effectif.
!


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 3 - Caractéristiques de dispersion
2-2-2 Variance et écart-type
C'est la moyenne de la somme des carrés des écarts à la moyenne
| nombre d'enfants | effectif |
|---|---|
| 1 | 9 |
| 2 | 5 |
| 3 | 5 |
| 4 | 1 |
| TOTAL | =20 |
variable quantitative discrète: tableau de dénombrement
soit le nombre de ligne du tableau, l'effectif total et la moyenne


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 3 - Caractéristiques de dispersion
2-2-2 Variance et écart-type
C'est la racine carré de la variance.
• S'exprime dans la même unité que la variable.
• Utilisée pour mesurer la dispersion autour de la moyenne.
• Idéal pour comparer 2 séries statistiques qui ont la même moyenne.
• Sensible aux valeurs aberrantes (comme la moyenne)



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 2&3: Caractéristiques de tendance centrale et de dispersion
Caractériser une variable quantitative
Caractéristiques de tendance centrale / de position:
-
=MOYENNE(plage)
-
=MEDIANE(plage)
-
=MODE(plage) Attention ne retourne qu’une valeur, il vaut peut être mieux le(s) définir en observant la variable ordonnée.
Caractéristiques de dispersion:
-
=MAX(plage)-MIN(plage)
-
=VAR(plage) Attention le calcul se fait sur N-1 car basé sur un “échantillon”, sinon utiliser =VARP(plage)
-
=ECARTYPE(plage) Attention même remarque: =ECARTYPEP(plage)
-
=QUARTILE(plage; type) pour Q1 c’est donc =QUARTILE(plage; 1).. calculer les Q1, Q2, Q3
-
écart/intervalle Inter-Quartile


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.2
Chapitre 3 - Caractéristiques de dispersion
2-2-2 Variance et écart-type
Le coefficient de variation
-
Le coefficient de variation est la proportion de l'écart-type par rapport à la moyenne.
-
Il permet de comparer la dispersion de deux distributions dont l'unité de mesure est différente.
-
Il s'exprime généralement en pourcentage.
-
Plus le coefficient de variation est proche de 1 (100%) plus la dispersion est importante.


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.3
Variable Quantitative Continue : Représentation Graphique
Les représentations graphiques d’une variable continue ont toutes en commun de permettre d’explorer la distribution de la variable , en identifiant:
-
la forme de la distribution
-
les concentrations
-
les dispersions
-
les ruptures dans la distribution


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.3
Variable Quantitative Continue : Représentation Graphique



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
3.3
Variable Quantitative Continue : Représentation Graphique
C'est la moyenne de la somme des carrés des écarts à la moyenne



Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.0
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
Chapitre 3 - Liaison entre 2 variables définie par un tableau de contingence
3-1-1 Tableau de contingence
3-1-2 Effectif conjoint
3-1-3 Fréquence conjointe
3-2-2 Fréquence marginale
3-2-1 Effectif marginal


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.1
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-1 Distribution conjointe: tableau de contingence
C'est un tri croisé entre 2 variables d'une même distribution statistique.
On l'appelle distribution conjointe ou distribution bi-variée.
| nombre d'enfants | agriculteur | menuisier | marchand | militaire |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 2 | 0 | 0 | 1 |
profession
variable
= Quantitative Absolue Discrète
avec modalités.
variable
=Qualitative
Nominale
Discrète
avec
modalités


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.1
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-1 Distribution conjointe: effectif conjoint
| nombre d'enfants | agriculteur | menuisier | marchand | militaire |
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 2 | 0 | 0 | 1 |
profession
est l'effectif conjoint du couple
c'est à dire l'effectif de l'observation pour laquelle:
la variable prend la modalité et
la variable prend la modalité
note: l'effectif total de la population est noté ou


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.1
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-1 Distribution conjointe: fréquence conjointe
| nombre d'enfants | agriculteur | menuisier | marchand | militaire |
|---|---|---|---|---|
| 1 | 0% | 0% | 10% | 0% |
| 2 | 10% | 0% | 10% | 0% |
| 3 | 10% | 10% | 10% | 10% |
| 4 | 20% | 0% | 0% | 10% |
profession
est la fréquence conjointe du couple
c'est à dire la fréquence de l'observation pour laquelle:
la variable prend la modalité et
la variable prend la modalité
(x100 si on l'exprime en %)


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.2
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-2 Distributions marginales:
| nombre d'enfants | agriculteur | menuisier | marchand | militaire | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 2 |
| 3 | 1 | 1 | 1 | 1 | 4 |
| 4 | 2 | 0 | 0 | 1 | 3 |
| 4 | 1 | 3 | 2 | 10 |
profession
De la distribution statistique du couple
on peut déduire la distribution de et la distribution de


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.2
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-2 Distributions marginales: effectif marginal
| nombre d'enfants | agriculteur | menuisier | marchand | militaire | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 2 |
| 3 | 1 | 1 | 1 | 1 | 4 |
| 4 | 2 | 0 | 0 | 1 | 3 |
| 4 | 1 | 3 | 2 | =10 |
profession
l'effectif marginal de l'observation
est le nombre d'individus présentant la modalité (ou la valeur) quelle que soit la valeur prise par la variable .
Elle est notée
effectifs marginaux de
effectifs marginaux de


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.2
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-2 Distributions marginales: fréquence marginale
| nombre d'enfants | agriculteur | menuisier | marchand | militaire | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 10% | 0 | 10% |
| 2 | 10% | 0 | 10% | 0 | 20% |
| 3 | 10% | 10% | 10% | 10% | 40% |
| 4 | 20% | 0 | 0 | 10% | 30% |
| 40% | 10% | 30% | 20% | =100% |
profession
exemple: la fréquence marginale de l'observation
est la fréquence relative des individus présentant la modalité (ou la valeur) par rapport à l'effectif total de la population, et ce quelle que soit la valeur prise par la variable .
Elle est notée
fréquences marginales de
fréquences marginales de


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.2
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-2 Distributions marginales: effectif marginal
| nombre d'enfants | agriculteur | menuisier | marchand | militaire | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 2 |
| 3 | 1 | 1 | 1 | 1 | 4 |
| 4 | 2 | 0 | 0 | 1 | 3 |
| 4 | 1 | 3 | 2 | =10 |
profession
l'effectif marginal de l'observation
est le nombre d'individus présentant la modalité (ou la valeur) quelle que soit la valeur prise par la variable .
Elle est notée
effectifs marginaux de


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.2
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-2 Distributions marginales: moyenne marginale
| nombre d'enfants | agriculteur | menuisier | marchand | militaire | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 2 |
| 3 | 1 | 1 | 1 | 1 | 4 |
| 4 | 2 | 0 | 0 | 1 | 3 |
| 4 | 1 | 3 | 2 | =10 |
profession
la moyenne marginale de c'est la moyenne arithmétique de la distribution marginale de
effectifs marginaux de
les ménages ont en moyenne 2.9 enfants (quelle que soit leur profession)


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.2
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-2 Distributions marginales: variance marginale
| nombre d'enfants | agriculteur | menuisier | marchand | militaire | |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 2 |
| 3 | 1 | 1 | 1 | 1 | 4 |
| 4 | 2 | 0 | 0 | 1 | 3 |
| 4 | 1 | 3 | 2 | =10 |
profession
la variance marginale de c'est la variance de la distribution marginale de
effectifs marginaux de


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-3 Distribution conditionnelle: effectif conditionnel
| nombre d'enfants | effectifs |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| total | 4 |
profession=agriculteur
On fixe une colonne (ou une ligne) et on observe l'effectif de la variable quand
exemple: on observe le nombre de ménage pour chaque catégorie (nombre d'enfants) parmi les individus de profession "agriculteur"


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-3 Distribution conditionnelle: fréquence conditionnelle
| nombre d'enfants | effectifs | fréquence |
|---|---|---|
| 1 | 0 | 0 % |
| 2 | 1 | 25 % |
| 3 | 1 | 25 % |
| 4 | 2 | 50 % |
| total | 4 | 100 |
profession=agriculteur
On fixe une colonne (ou une ligne) et on calcule la fréquence de la variable quand
exemple: on calcule la fréquence du nombre de ménage pour chaque catégorie (nombre d'enfants) parmi les individus de profession "agriculteur"


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-3 Distribution conditionnelle: moyenne conditionnelle
| nombre d'enfants | effectifs |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| total | 4 |
profession=agriculteur
On fixe une colonne (ou une ligne) et on calcule la moyenne de la variable quand
exemple: on calcule la moyenne du nombre d'enfants dans les ménages dont la profession est "agriculteur"


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-3 Distribution conditionnelle: variance conditionnelle
| nombre d'enfants | effectifs |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| total | 4 |
profession=agriculteur
On fixe une colonne (ou une ligne) et on calcule la variance de la variable quand
exemple: on calcule la variance du nombre d'enfants dans les ménages dont la profession est "agriculteur"


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-4 Relations entre distribution marginales et conditionnelles
Décomposition de la variance marginale de
Variance marginale
de X
variance des moyennes conditionnelles de X
moyenne des variances conditionnelles de X
+
=
=
variance expliquée
variance résiduelle
+
=
variance inter-groupes
variance intra-groupes
+
soit
soit
soit


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-4 Relations entre distribution marginales et conditionnelles
Rapport de détermination de X en fonction de Y :
- Exprime la proportion de la variance marginale de X représentée par la variance des moyennes conditionnelles de X (variance expliquée)
- Calcule l'influence de la variable Y sur la variabilité de la variable X
- Valeur comprise entre 0 et 1, exprimée en % (donc à multiplier par 100).
Exemples : influence du "type d'acheteur" sur la variabilité du "prix de de la vente de terre (exercice 2.1)
influence du "sexe" sur la variabilité de la taille des individus (exercice 2.2)


Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
sylvain.badey@univ-tours.fr
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-4 Relations entre distribution marginales et conditionnelles
Rapport de détermination
variance des moyennes conditionnelles de X
variance marginale
/
=
=
variance expliquée
variance marginale
/
=
variance inter-groupes
variance marginale
/
soit
soit
soit

Histoire Licence 2 - MO44 - EP1
Statistiques pour historiens et archéologues
4.3
Chapitre 4 - Liaison entre 2 variables définie par un tableau de contingence
3-4 Relations entre distribution marginales et conditionnelles
Rapport de corrélation
Initiation aux statistiques descriptives univariées


variable continue RG
3/7
Variable Quantitative Continue : Représentation Graphique
Scalogramme (ou Matrice Ordonnée)
• Représentation élémentaire et unidimensionnelle (il n’y a qu’un axe: celui des abscisses) d’une distribution statistique, consistant à représenter chaque élément de la distribution par un point sur un axe gradué.
• Lorsque deux éléments ont des modalités identiques ou très proches, on procède à un " empilement " des points.
• Permet de discerner efficacement les minima et maxima, la forme de la distribution, les concentrations, les dispersions et les ruptures.

Initiation aux statistiques descriptives univariées


variable continue RG
4/7
Variable Quantitative continue : Représentation Graphique
Scalogramme
Fichier stature.ods
Dans Calc, d'après votre tableau de distribution:
Représenter sous forme de Scalogramme la variable continue "taille"

Initiation aux statistiques descriptives univariées


variable continue RG
5/7
Variable Quantitative Continue : Représentation Graphique
Diagramme en tige et feuille
• Tige = partie entière du nombre décimal OU extraction des dizaines.
• Feuilles = chiffre décimal OU chiffre des unités.
• Permet de distinguer les minimum et maximum, le(s) mode(s) et la forme générale de distribution.
14 | 01
14 | 566777899
15 | 0011111222223333334444
15 | 56666666666777778888889999999
16 | 000000111122222233344
16 | 55555566677777788888888999999999
17 | 00000011111222334444
17 | 5555555666689
18 | 014
18 |
19 | 1
• A mi chemin entre le tableau et le graphique ce diagramme.
• Revient à faire un regroupement de la variable continue en classes d'amplitudes égales.
Initiation aux statistiques descriptives univariées


variable continue RG
6/7
Variable Quantitative Continue : Représentation Graphique
Courbes de fréquences cumulées
Interprétation:
• Pente forte = concentration
• Pente faible = dispersion
• Marche d'escalier = Rupture

C'est un graphique bi-dimensionnel représentant en abscisse les modalités du caractère continu étudié et en ordonnée, les fréquences cumulées
Initiation aux statistiques descriptives univariées


variable continue RG
7/7
Variable Quantitative Continue : Représentation Graphique
Courbes de fréquences cumulées
Dans Calc,
1. Compléter le tableau de distribution avec les colonnes suivantes:
- la fréquence relative (part de chaque modalité par rapport au total)
- la fréquence cumulée ascendante (doit finir à 100% pour le dernier individu)
- la fréquence cumulée descendante (doit finir à 0% pour le dernier individu)
2. Représenter sous forme de Courbes de fréquence cumulées la variable continue "taille"

Initiation aux statistiques descriptives univariées


introduction 2/7
Acquérir les bases du vocabulaire de statistique afin de pouvoir décrire clairement ces données et de savoir les préparer en vue d'une analyse descriptive simple.
Maîtriser les outils de type tableur et spécialisés pour l'analyse et la représentation graphique en respectant les règles de la sémiologie graphique (et de l’honnêteté scientifique).
Approcher la démarche statistique au travers d'un exemple : la discrétisation afin d'effectuer une analyse par maille





Initiation aux statistiques descriptives univariées


introduction
4/7
Jour 1
Introduction
Qu'est ce que la statistique ?
Utilisation d'un tableur
Première découverte du logiciel
Jour 2
Vocabulaire statistique
Qualifier une variable
Préparation / Consolidation des données
Analyser et représenter une variable discrète
Jour 3
Analyser et représenter une variable continue
Jour 4
Analyser et représenter une variable continue (suite)
Jour 5
Discrétisation et Analyse par maille
Démarche classique de statistique descriptive : depuis la préparation des données jusqu'à leur description et représentations.
Utilisation de logiciels libres pour:
- sortir de nos habitudes
- travailler avec n'importe quel ordinateur (personnel, professionnel)
- travailler avec des collaborateurs externes
- assurer la pérennité de nos données
Initiation à la reproductibilité de la démarche statistique
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
2/10
Dans le dossier STATS_OK > créer un nouveau dossier Travail
Faire une copie du Fichier Donnees/data_calc.ods dans le dossier Travail
Ouvrir LibreOffice Calc





Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
1/10

Utilisation d'un tableur : LibreOffice Calc
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
3/10
A partir de la feuille exo_vente:
Collage spécial
Coller les valeurs de la colonne F "gain TTC" dans une nouvelle feuille demo_exo
Chercher-Remplacer
Remplacer computer par ordinateur
Remplacer matos par matériel
Remplacer pelle par pelles
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
4/10
A partir de la feuille data_RTP:
Formules et fonctions
1. Addition : calculer le total d’Os par structure
2. Somme : A l’échelle du site, calculer la somme de céramique, d'Os de bœuf, de cochon, de mouton et autres.
3. Fréquence : Calculer la fréquence d’Os de bœuf, de cochon, de mouton par rapport à la totalité des Os par structure.
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
5/10
A partir de la feuille data_SE:
Concaténation simple
Concaténer les champs "forme en plan" et "forme en coupe"
Concaténation complexe
Dans un champ "description" écrivez, pour chaque structure, selon le modèle: « la structure a un plan circulaire et une coupe en V »
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
6/10
A partir de la feuille data_RTP:
Opérateurs logiques
Déterminer le nombre de structures de type BBQ
Sachant que ces structures se définissent par:
- Un nombre d’Os supérieur au nombre de céramique.
- La présence de phosphate.
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
7/10
A partir de la feuille budget_datation:
Opérateurs logiques (2)
1. Déterminez votre budget analyse C14 sachant:
- Que les datations se font sur les faits possédant un dessin et au moins du charbon ou une graine
- Le prix d'une datation est de 300 €
2. Quel est le montant global de vos datations ?
Facultatif
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
8/10
A partir de la feuille data_SE:
Tris
1. Trier les faits par le nombre de fragments céramiques qu’il contiennent (tri ascendant).
2. Trier les faits par type et diamètre (tris ascendants).
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
9/10
A partir de la feuille data_SE:
Déterminer à l'aide des Filtres
1. Le nombre de TP avec une forme ovale en plan.
2. Le nombre de silo avec une forme en plan circulaire et un diamètre supérieur à 1,2 m.
Initiation aux statistiques descriptives univariées


Utilisation d'un tableur
10/10
A partir de la feuille data_SE:
Tableau Croisé
1. Calculer la somme des fragments de céramique par type de faits et par périodes.
2. Calculer le diamètre moyen des types de faits par périodes.
3. Calculer la profondeur moyenne des silos de l’Antiquité.
Consolidation et préparation du jeu de données…
nettoyage

1. Individus en ligne / Variables en colonnes
2. Pas de doublons
3. Noms de variables : courts, clairs, sans accents, sans espaces, en minuscule
4. Pas de caractères spéciaux $ % ° @ #
5. Données manquantes = cellule vide
6. Incertitude = ajouter une colonne commentaire
7. Un seul séparateur de décimales . ou ,
8. Pas de mise en forme
9. Exporter en CSV
10. Vérifier/Relire ses données (consolidation
des données/coquilles)

source: "Éléments de Statistiques" de F.Santos - http://www.pacea.u-bordeaux1.fr/IMG/pdf/poly_cours.pdf
Initiation aux statistiques descriptives univariées


variable continue RN
1/11
Variable Quantitative continue : Représentation Numérique
Tableau de distribution (début)
• Le tableau de distribution statistique est un simple reclassement du tableau élémentaire.
• Il s’agit d’un tableau élémentaire dans lequel les valeurs du caractère X ont été ordonnées en ordre croissant.


Initiation aux statistiques descriptives univariées


variable continue RN
2/12
Variable Quantitative continue : Représentation Numérique
Tableau de distribution
A partir du fichier stature.ods dans le dossier
Dans Calc:
1. Créer une nouvelle feuille taille
2. Copier la colonne correspondant à la variable continue "taille"
3. Trier la variable "taille" par ordre croissant

Initiation aux statistiques descriptives univariées


Sémiologie
1/17
Représentation Graphique
Quelques règles et recommandations
1. Vérifier les données et donner un titre
2. Supprimer toute information non utile et minimiser l’information secondaire.
3. Supprimer les effets inutiles
4. Ajuster les échelles
5. Choisir les couleurs
Initiation aux statistiques descriptives univariées


Sémiologie
2/17
William Playfair (1759-1823) ingénieur et économiste
Ecossais

les proportions de l'Empire Ottoman en Asie, Europe et Afrique avant 1789.
in Statistical Breviary (1801)
Initiation aux statistiques descriptives univariées


Sémiologie
3/17
Charles Joseph MINARD (1781-1870) inspecteur des ponts et chaussées
Français

La Campagne de Russie de Napoléon de 1812 à1813 (1869)
Voir aussi 1812 When Napoleon Ventured East
Initiation aux statistiques descriptives univariées


Sémiologie
4/17
Tonnage des grands ports et principale rivières d'Europe (1859)
Initiation aux statistiques descriptives univariées


médecin épidémiologiste britannique

Initiation aux statistiques descriptives univariées


Sémiologie
6/17
Sémiologie Graphique
C'est l’ensemble des règles qui permettent l’usage d’un système de signes graphiques pour transmettre l’information »

Un ouvrage de référence : « sémiologie graphique » de Jacques Bertin, publié en 1967.
Jacques Bertin (1918-2010) Cartographe Français
Initiation aux statistiques descriptives univariées


Sémiologie
7/17

Initiation aux statistiques descriptives univariées


Sémiologie
8/17


Initiation aux statistiques descriptives univariées


Sémiologie
9/17



Initiation aux statistiques descriptives univariées


Sémiologie
10/17




Initiation aux statistiques descriptives univariées


Sémiologie
11/17
Représentation Graphique
Règles de sémiologie graphique

Initiation aux statistiques descriptives univariées


Sémiologie
12/17
Association
Sélection
Qualitatif
Nominal
- Exprime des différences non ordonnables
- Très lisible
- Variable qui permet de mieux séparer des figurés représentant des objets de nature différente
- Pas plus de 6 à 7 couleurs différentes.
- Limiter l’emploi de la couleur.
COULEUR
Initiation aux statistiques descriptives univariées


Sémiologie
13/17
Association
Sélection
Qualitatif
Nominal
COULEUR


Initiation aux statistiques descriptives univariées


Sémiologie
14/17
Ordre
Qualitatif
Ordinal
- = quantités totales de noir et de blanc dans une surface
- Uniquement pour représenter une information ordonnée : du clair au foncé = du faible au fort
- Représente des rapports de proportion.
- Jamais des effectifs => elle ne permet pas d’évaluer les rapports entre les nombres représentés
- 6 à 7 valeurs de gris différentes maximum (y compris B et N
VALEUR
Quantitatif
Relatif
O
Initiation aux statistiques descriptives univariées


Sémiologie
15/17
Qualitatif
Ordinal
VALEUR
Quantitatif
Relatif

Ordre
O
Initiation aux statistiques descriptives univariées


Sémiologie
16/17
Quantité
(proportionnalité)
Quantitatif
Absolu
- Seule variable visuelle qui traduit directement les quantités et qui permet d’estimer les rapports qui existent entre elles
- Elle est ordonnée
- Porte sur la longueur, la largeur ou la surface des figurés
- Le cerveau humain distingue moins bien une proportion entre deux surfaces qu’entre deux longueurs.
TAILLE
Q
Initiation aux statistiques descriptives univariées


Sémiologie
17/17
Quantité
(proportionnalité)
Quantitatif
Absolu
TAILLE
Q


exemples d'anamorphoses d'après les taux de représentations des régions anatomiques de différentes sépultures collectives (H.Guy, M.Gaultier)
Initiation aux statistiques descriptives univariées


Représentation
Jeu
1/14
Représentation Graphique
On joue ?
1. Identifier la nature des variables statistiques représentées
2. Identifier les variables visuelles utilisées
3. Chercher les erreurs de représentations (si elles existent)
4. Proposer des alternatives
Initiation aux statistiques descriptives univariées


Représentation
Jeu
2/14
Représentation Graphique - On joue ?

Initiation aux statistiques descriptives univariées


Représentation
Jeu
3/14
Représentation Graphique - On joue ?

distribution spatiale des éléments lithiques (in Archaeological Investigations between Cayenne Island and the Maroni River)
Initiation aux statistiques descriptives univariées


Représentation
Jeu
4/14
Représentation Graphique - On joue ?


Initiation aux statistiques descriptives univariées


Représentation
Jeu
5/14
Représentation Graphique - On joue ?

représentation des parties anatomiques des équidés sur différents sites
Initiation aux statistiques descriptives univariées


Représentation
Jeu
6/14
Représentation Graphique - On joue ?
Représentation du cheval au sein des assemblages osseux d'équidés de l'Antiquité à la période Carolingienne (indice 100 à La Tène Finale)

Initiation aux statistiques descriptives univariées


Représentation
Jeu
7/14
Représentation Graphique - On joue ?
Évolution comparée de la stature des mammifères domestiques (indice 100 à La Tène Finale)

Initiation aux statistiques descriptives univariées


Représentation
Jeu
8/14
Représentation Graphique - On joue ?
Principales composantes topographiques représentées sur les tracés d'autoroute (in RAP 2014)

Initiation aux statistiques descriptives univariées


Représentation
Jeu
9/14
Représentation Graphique - On joue ?
Importations de fromage au Canada en 2016 (in Les Echos - déc. 2017)

Initiation aux statistiques descriptives univariées


Représentation
Jeu
11/14
Représentation Graphique - On joue ?
Budget de l'état français en 2016
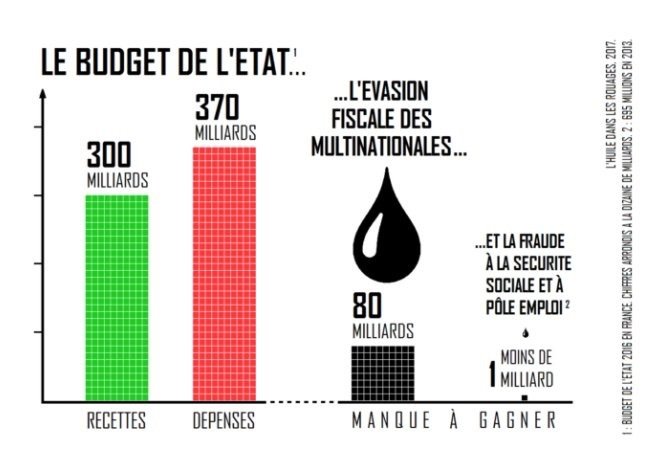
Initiation aux statistiques descriptives univariées


Représentation
Jeu
12/14
Représentation Graphique - On joue ?
Répartition de types de céramiques par matières premières

Initiation aux statistiques descriptives univariées


Représentation
Jeu
13/14
Représentation Graphique - On joue ?
Répartition des types de céramiques par carrés de fouille

Initiation aux statistiques descriptives univariées


Représentation
Jeu
14/14
Représentation Graphique - On joue ?

Initiation aux statistiques descriptives univariées


Histogramme
1/7
Variable Quanitative Continue : Représentation Graphique
Construire un Histogramme
1. Définir le nombre de classes
2. Choisir une méthode de découpage des classes (discrétisation)
3. Construire un Tableau de dénombrement
4. Réaliser l'Histogramme
Initiation aux statistiques descriptives univariées


Histogramme
2/7
Histogramme
Définir le nombre de classes
Quelques formules magiques:
1. Racine Carré
2. La règle de Sturges
3. La formule de Freedman-Diaconis
=RACINE(N)
=1+LOG(N;2)
=(MAX(plage)-MIN(plage))/(2*(QUARTILE(plage;3)-QUARTILE(plage;1))*PUISSANCE(N;-1/3))

Initiation aux statistiques descriptives univariées


Histogramme
3/7
Histogramme : Définir le nombre de classes
Créer une nouvelle feuille Histo
Copier la colonne "taille" triée par ordre croissant
Calculer le nombre de classes maximum pour la variable "taille" avec les formules:
1. Racine Carré
2. Sturges
3. Freedman-Diaconis
=RACINE(N)
=1+LOG(N;2)
=(MAX(plage)-MIN(plage))/(2*(QUARTILE(plage;3)-QUARTILE(plage;1))*PUISSANCE(N;-1/3))

Stat - Histoire Licence2
By Formation_SIG
Stat - Histoire Licence2
TD de statistique pour historiens et archéologues de l'université de Tours (Licence 2 mention Histoire)
- 3,043