Recursion
Arvin Liu
一個方便找投影片的目錄
Syllabus - 0
| 內容 | 快速連結 |
|---|---|
| What is Recursion? 什麼是遞迴呢？ | Section 1 |
| Recursion Tree 用遞迴樹想像遞迴的過程 | Section 2 |
| Ex O - 遞迴觀念題 | Section 3 |
| Ex I - 遞迴觀念題練習 如何將數學遞迴程式遞迴？ | Section 4 |
| Recursion Tips 遞迴要注意的事項 | Section 5 |
| Ex II - 彩帶問題 從排列組合到遞迴 | Section 6 |
| Memorization - 記憶化 一個讓遞迴更快的重要技巧 | Section 7 |
| Euclidean Algorithm - 輾轉相除法 | Section 8 |
| Exercise III - Rhythm Doctor | Section 9 |
| 零和問題 嘗試用遞迴暴搜索有可能！ | Section 10 |
| Pruning - 剪枝一個大家都會，但很重要的技巧 | Section 11 |
| Talks - 結語 | Section 12 |
重要章節
主要章節
這個投影片怎麼用呢？
Before Before Class - 0
- 上下左右切換投影片，用ESC可以看到整個投影片的大綱。
- 每個直排都是一個主題，右上角有編號，你可按右上角的 回第一頁。
- 正確觀看順序：一直往下，到底往右。
Esc後大概長這樣，你可以先Esc在上下左右選你要看哪頁投影片。
What is Recursion?
什麼是遞迴呢?
先讓我們看段影片...
What is Recursion ? - 0
我們從這段影片學到了甚麼？
What is Recursion ? - 1
- 遞迴定義：每個人遇到問題的時候，都會跑去問他的上級。
- 店員遇到解決不了的問題，就該去問經理。
- 經理遇到解決不了的問題，就該去問老闆。
- ....
- 基本情況 (Base case)：God能夠解決一切。
什麼是遞迴呢?
What is Recursion ? - 2
Recursion
一個經典的例子 - 斐波那契數列
What is Recursion ? - 4
Fibonacci Sequence
⎩⎨⎧F1=1F2=1Fn=Fn−1+Fn−2
\begin{cases}
F_1 = 1 \\
F_2 = 1 \\
F_n = F_{n-1} + F_{n-2} \\
\end{cases}
f(n)={1,if n=1or 2f(n−1)+f(n−2),otherwise
f(n)=
\begin{cases}
1, \text{if \,n=1\,or \,2}\\
f(n-1)+f(n-2), \text{otherwise}
\end{cases}
- 寫成這樣也OK (在數學上)。
*otherwise: 否則的意思
- 常見的表達式長這樣:
這怎麼看呢?
F4=F3+F2
F_4 = F_3 + F_2
F3=F2+F1
F_3 = F_2 + F_1
=1+1=2
= 1 + 1 = 2
=2+1=3
= 2 + 1 = 3
一個經典的例子 - 斐波那契數列
What is Recursion ? - 5
Fibonacci Sequence
f(n)={1,if n=1or 2f(n−1)+f(n−2),otherwise
f(n)=
\begin{cases}
1, \text{if \,n=1\,or \,2}\\
f(n-1)+f(n-2), \text{otherwise}
\end{cases}
- 寫成這樣也OK (在數學上)。
*otherwise: 否則的意思
int f(int n){ if(n == 1 || n == 2) return 1; else return f(n-1) + f(n-2); }
- 程式就當作你在寫一般的函式，照著寫就可以了。
一個經典的例子 - C(n, m)
What is Recursion ? - 6
C(n,m)={1,if m=0or n=mC(n−1,m−1)+C(n−1,m),otherwise
C(n, m)=
\begin{cases}
1, \text{if \,m=0\,or n=m}\\
C(n-1, m-1)+C(n-1, m), \text{otherwise}
\end{cases}
- 什麼是C呢? C(n, m) 就是從n個相異東西取出m個的取法總數。
- 舉例來說，如果從下面4顆球取出2顆球出來，總共有6種取法。
- 那麼我們 C(4, 2) 就會等於6。
C(n, m)其實是有遞迴公式的，長的像下面這樣。
有4顆相異的球
一個經典的例子 - C(n, m)
What is Recursion ? - 7
C(n,m)={1,if m=0or n=mC(n−1,m−1)+C(n−1,m),otherwise
C(n, m)=
\begin{cases}
1, \text{if \,m=0\,or n=m}\\
C(n-1, m-1)+C(n-1, m), \text{otherwise}
\end{cases}
- 那麼我們 C(4, 2) 就會等於6。
C(n, m)其實是有遞迴公式的，長的像下面這樣。
- 為甚麼呢?
- C(n, m): 從n顆球取m顆的取法
- 如果我取了第一顆球，那麼總數會是 "從n-1顆球取m-1顆"，C(n-1, m-1)。
- 如果我不取第一顆球，那麼總數會是 "從n-1顆球取m顆"，C(n-1, m)。
- 這樣你懂為什麼了嗎？
- C(n, m): 從n顆球取m顆的取法
一個經典的例子 - C(n, m)
What is Recursion ? - 8
- 那麼我們 C(4, 2) 就會等於6。
C(n, m)其實是有遞迴公式的，長的像下面這樣。
- 如同剛剛的例子一樣，轉成程式直接照著寫就好了。
int C(int n, int m){ if(n == 0 || n == m) return 1; else return C(n-1, m-1) + C(n-1, m); }
C(n,m)={1,if m=0or n=mC(n−1,m−1)+C(n−1,m),otherwise
C(n, m)=
\begin{cases}
1, \text{if \,m=0\,or n=m}\\
C(n-1, m-1)+C(n-1, m), \text{otherwise}
\end{cases}
Recursion Tree
遞迴樹 - 遞迴要怎麼想像呢?
怎麼分析遞迴呢?
What is Recursion Tree ? - 0
Recursion
- 你大致上可以把遞迴看成是一個分支圖，舉例來說，我們呼叫了f(5)：
f(n)={1,if n=1or 2f(n−1)+f(n−2),otherwise
f(n)=
\begin{cases}
1, \text{if \,n=1\,or \,2}\\
f(n-1)+f(n-2), \text{otherwise}
\end{cases}
f(5)=⎩⎨⎧f(4)=⎩⎨⎧f(3)=⎩⎨⎧f(2)=1+f(1)=1+f(2)=1+f(3)={f(2)=1f(1)=1
f(5)=
\begin{cases}
f(4) = \begin{cases}
f(3) = \begin{cases}f(2) = 1\\+\\f(1) = 1 \end{cases}\\ +\\f(2) = 1\end{cases}\\ + \\ f(3) = \begin{cases} f(2) = 1 \\ f(1) = 1\end{cases}\end{cases}
1
2
3
4
5
6
7
8
9
- 紫色數字是呼叫的順序
- 如果有兩個f，函式會先做完第一個再去做第二個。
- 所以答案為5。
怎麼分析遞迴呢?
What is Recursion Tree ? - 1
Recursion
- 試試看畫出C(4, 2)的分析圖吧！
C(n,m)={1,if m=0or n=mC(n−1,m−1)+C(n−1,m),otherwise
C(n, m)=
\begin{cases}
1, \text{if \,m=0\,or n=m}\\
C(n-1, m-1)+C(n-1, m), \text{otherwise}
\end{cases}
C(4,2)=⎩⎨⎧C(3,1)=⎩⎨⎧C(2,0)=1+C(2,1)=⎩⎨⎧C(1,0)=1+C(1,1)=1+C(3,2)=⎩⎨⎧C(2,1)=⎩⎨⎧C(1,0)=1+C(1,1)=1+C(2,2)=1
C(4, 2)=
\begin{cases}
C(3, 1) =
\begin{cases}
C(2, 0) = 1 \\
+ \\
C(2, 1) =
\begin{cases}
C(1, 0) = 1\\
+ \\
C(1, 1) = 1
\end{cases}
\end{cases} \\
+ \\
C(3, 2) =
\begin{cases}
C(2, 1) =
\begin{cases}
C(1, 0) = 1\\
+ \\
C(1, 1) = 1\\
\end{cases} \\
+ \\
C(2, 2) = 1
\end{cases}
\end{cases}
- 所以答案為6。
- 你會發現一件事情，在分析的時候，有些遞迴會重複，這個時候用之前算過的值就好了。
- 例如C(2, 1)有算過兩次，第二次直接看第一次算的值(=2)就好了。
為甚麼要叫遞迴樹呢?
What is Recursion Tree ? - 2
Tree
樹根
樹葉
- 起先，你以為樹是往上長的。
- 但在程式 / 資料結構裡面，樹是往下長的。
- 遞迴的分支圖，其實就是一棵樹，我們可以叫它遞迴樹。
樹葉
樹根
Exercise O
APCS的手寫遞迴題
Exercise O
APCS 手寫練習題
接下來有三題APCS手寫題。
- 在寫之前請各位拿出一張紙方便計算。
- 每一題只能寫2分鐘。
- 這裡沒有給選項。
APCS 106/03 觀念題 - 21
Exercise O - APCS遞迴手寫題1 - 0
int F (int x, int y) { if (x<1) return 1; else return F(x-y, y) + F(x-2*y, y); }
21. 若以 F(5,2) 呼叫下方 F() 函式，執行完畢後回傳值為何?
F(5, 2) = F(3, 2) + F(1, 2)
F(3, 2) = F(1, 2) + F(-1, 2)
F(1, 2) = F(-1, 2) + F(-3, 2)
= 1 + 1 = 2
= 2 + 1 = 3
= 3 + 2 = 5
→ 答案 = 5
2 mins
APCS 105/03 觀念題 - 24
Exercise O - APCS遞迴手寫題2 - 1
int f (int n) { if (n > 3) { return 1; } else if (n == 2) { return (3 + f(n+1)); } else { return (1 + f(n+1)); } }
24. 若以 g(4) 呼叫 g() 函式，執行完畢後回傳值為何?
int g (int n) { int j = 0; for (int i=1; i<=n-1; i=i+1) { j = j + f(i); } return j; }
- g(4)答案會等於多少呢?
= f(1) + f(2) + f(3)。 - 那麼f(1)又是多少呢?
好像不太容易看出來...
2 mins
APCS 105/03 觀念題 - 24
Exercise O - APCS遞迴手寫題2 - 2
int f (int n) { if (n > 3) { return 1; } else if (n == 2) { return (3 + f(n+1)); } else { return (1 + f(n+1)); } }
24. 若以 g(4) 呼叫 g() 函式，執行完畢後回傳值為何?
int g (int n) { int j = 0; for (int i=1; i<=n-1; i=i+1) { j = j + f(i); } return j; }
- g(4)答案會等於多少呢?
= f(1) + f(2) + f(3)。 - 那麼f(1)又是多少呢?
好像不太容易看出來... - f(1) = 1 + f(2)
- f(2) = 3 + f(3)
- f(3) = 1 + f(4)
- f(4) = 1
- 答案 = 13
= 6
= 5
= 2
= 6 + 5 + 2
2 mins
APCS 107/12 觀念題 - 03
Exercise O - APCS遞迴手寫題3 - 3
int K (int a[], int n) { if (n >= 0) return (K(a, n-1) + a[n]); else return 0; } int G (int n) { int a[] = {5, 4, 3, 2, 1}; return K(a, n); }
3. 給定右側 G(), K() 兩函式，執行 G(3) 後所回傳的值為何？
2 mins
- G(3)會呼叫K(a, 3)。
- K(a, 3) = K(a, 2) + a[3]
- K(a, 2) = K(a, 1) + a[2]
- K(a, 1) = K(a, 0) + a[1]
- K(a, 0) = K(a, -1) + a[0]
- K(a, -1) = 0
- 答案 = a[0] + a[1] + a[2] + a[3] = 14
Exercise I
警報器 - 簡單的遞迴練習
Exercise I
程式練習題
接下來有一題請你用
程式實做遞迴的題目。
- 我會花1分鐘讀題。
- 總共計時10分鐘。
- 開好你的程式環境吧！
226 - 警報器 - 題目
Exercise I - 警報器 - 0
- 題目：請問警報器長鳴為一次需3秒，短鳴一次需1秒，每格鳴聲之間停2秒，若鳴聲時間為t秒 (開頭跟結尾必須是鳴聲，不能是間隔的2秒)，
那麼請問有多少種信號?
(t為1到100的正整數。)
f(t)=⎩⎨⎧1,if t=1, or t=30,if t≤0f(t−5)+f(t−3),otherwise
f(t)=
\begin{cases}
1, \text{if \,} t = 1\text{, or }t = 3\\
0, \text{if \,} t \le 0\\
f(t-5)+f(t-3), \text{otherwise}
\end{cases}
- 小小提示，這題答案的遞迴式長這樣，你可以實作出來嗎？
10 mins
- t = 6總共有兩種可能。
3s
2s
1s
1s
2s
3s
226 - 警報器 - 解答
Exercise I - 警報器 - 1
f(t)=⎩⎨⎧1,if t=1, or t=30,if t≤0f(t−5)+f(t−3),otherwise
f(t)=
\begin{cases}
1, \text{if \,} t = 1\text{, or }t = 3\\
0, \text{if \,} t \le 0\\
f(t-5)+f(t-3), \text{otherwise}
\end{cases}
- 小小提示，這題答案的遞迴式長這樣，你可以實作出來嗎？
10 mins
int f(int t) { if (t == 1 || t == 3) return 1; else if (t <= 0) return 0; else return f(t-5) + f(t-3); }
- 轉成程式的話就是這樣。使用直接輸出 f(t)就可以了
226 - 警報器 - 引導
Exercise I - 警報器 - 2
f(t)=⎩⎨⎧1,if t=1, or t=30,if t≤0f(t−5)+f(t−3),otherwise
f(t)=
\begin{cases}
1, \text{if \,} t = 1\text{, or }t = 3\\
0, \text{if \,} t \le 0\\
f(t-5)+f(t-3), \text{otherwise}
\end{cases}
- 為甚麼題目可以寫成這樣的遞迴呢？
10 mins
- 在所有長度為t的鳴聲中其實可分為兩類，把這兩種可能加起來就可以了。
- 最後一段是長鳴。
- 最後一段是短鳴。
可能數 = 長度為t-5的鳴聲種數。
可能數 = 長度為t-3的鳴聲種數。
2s
1s
2s
3s
t-5 s的組合鳴聲
t-3 s的組合鳴聲
t s的組合鳴聲
Recursion Tips
遞迴要注意的事情
遞迴的題目要怎麼思考呢？
Recursion Tips - 遞迴要注意的事情 - 0
- 想辦法把大問題拆成小問題！
- 你可能要先定義問題本身，再想辦法達成這個問題的答案 (?)
- 思考的時候，
- 不要從一開始往上推，例如n=0怎麼樣，n=1怎麼樣...
- 通常情況下，要逆向思考，例如n要怎麼用n-1表示，或者n-2表示...
- 舉例來說，思考長度為t的鳴聲怎麼做時，我們要逆向思考。
- 想想長度為t的鳴聲怎麼用t-?的鳴聲來的得到。
- 而不是思考t=1要怎麼往上推到長度為t。
-
記的要思考基礎 / 終止條件！
- 不然遞迴會無止盡的跑下去，最終吃TLE或RE
記得要寫base case！
Recursion Tips - 遞迴要注意的事情 - 1
小心無窮遞迴！
Recursion Tips - 遞迴要注意的事情 - 2
Exercise II
彩帶問題 - 從遞迴到排列組合
Exercise II
程式練習題
接下來有一題請你用程式實做遞迴的應用題。
- 我會花1分鐘讀題。
- 總共計時15分鐘。
- 想一下前面教了什麼。
- 至少第一組測資要可以AC。
227 - 彩帶問題 - 題目
Exercise II - 彩帶問題 - 0
- 題目：現在Peipei要請你做出一個漂亮的彩帶，每一段你可以選擇三種顏色，分別是紅，橘，藍三種。至於何為漂亮呢？漂亮的彩帶有以下的限制：
- 不能有連續的紅色。
- 橘色後面一定要接藍色。
- 你可以告訴我們如果彩帶的長度為n (n介於1到50到之間的整數)，
有幾種可能的漂亮的彩帶呢？ (Hint：參數不只一個n。)
- 如果題目輸入的n為2，答案會是6種。
15 mins
227 - 彩帶問題 - 引導
Exercise II - 彩帶問題 - 1
-
我們試著以這樣的思維想想看：
-
在所有長度為n的漂亮彩帶的可能中，可以分成以下3個case。
- 最後一段為紅色的漂亮彩帶。
- 最後一段為橘色的漂亮彩帶。
- 最後一段的藍色的漂亮彩帶。
-
那麼在這3個case，分別會有幾種可能呢？
-
我們以最後一段為紅色做舉例
- 數量會等於長度為n-1，最後一段為藍色的漂亮彩帶的可能數。
-
我們以最後一段為紅色做舉例
-
在所有長度為n的漂亮彩帶的可能中，可以分成以下3個case。
15 mins
?
?
?
...
n-1
?
?
?
...
n-1
?
?
?
...
227 - 彩帶問題 - 引導
Exercise II - 彩帶問題 - 2
- 如果我們將長度為n，顏色為color定義成 rec(n, color)。
- rec(n, RED) = rec(n-1, BLUE)。
- rec(n, ORANGE) 和 rec(n, BLUE) 呢？
- rec(n, ORANGE) = rec(n-1, RED) + rec(n-1, BLUE)。
- rec(n, BLUE) = rec(n-1, RED) + rec(n-1, BLUE) + rec(n-1, ORANGE)。
-
終止條件呢？
- rec(1, 不管甚麼顏色) = 1
15 mins
?
?
?
...
n-1
?
?
?
...
?
?
?
...
?
?
?
...
n-1
?
?
?
...
?
?
?
...
227 - 彩帶問題 - 解答
Exercise II - 彩帶問題 - 3
// RED = 0, ORANGE = 1, BLUE = 2 long long rec(int n, int type) { if (n == 1) return 1; else if (type == RED) return rec(n-1, BLUE); else if (type == BLUE) return rec(n-1, ORANGE) + rec(n-1, BLUE) + rec(n-1, RED); else if (type == ORANGE) return rec(n-1, BLUE) + rec(n-1, RED); else // Should not reach here. return 0; }
- rec(n, RED) = rec(n-1, BLUE)。
- rec(n, ORANGE) = rec(n-1, RED), rec(n-1, BLUE)。
- rec(n, BLUE) = rec(n-1, RED) + rec(n-1, BLUE) + rec(n-1, ORANGE)。
- 終止條件：rec(1, 不管甚麼顏色) = 1。
227 - 彩帶問題 - 解答嗎(?)
Exercise II - 彩帶問題 - 4
// RED = 0, ORANGE = 1, BLUE = 2 long long rec(int n, int type) { if (n == 1) return 1; else if (type == RED) return rec(n-1, BLUE); else if (type == BLUE) return rec(n-1, ORANGE) + rec(n-1, BLUE) + rec(n-1, RED); else if (type == ORANGE) return rec(n-1, BLUE) + rec(n-1, RED); else // Should not reach here. return 0; }
- rec(n, RED) = rec(n-1, BLUE)。
- rec(n, ORANGE) = rec(n-1, RED), rec(n-1, BLUE)。
- rec(n, BLUE) = rec(n-1, RED) + rec(n-1, BLUE) + rec(n-1, ORANGE)。
- 終止條件：rec(1, 不管甚麼顏色) = 1。
怎麼會吃TLE呢??
Memoization
記憶化
遞迴怎麼可以這麼慢啊...
Memoization 記憶化 - 0
- 讓我們想想之前的遞迴樹。
C(4,2)=⎩⎨⎧C(3,1)=⎩⎨⎧C(2,0)=1+C(2,1)=⎩⎨⎧C(1,0)=1+C(1,1)=1+C(3,2)=⎩⎨⎧C(2,1)=⎩⎨⎧C(1,0)=1+C(1,1)=1+C(2,2)=1
C(4, 2)=
\begin{cases}
C(3, 1) =
\begin{cases}
C(2, 0) = 1 \\
+ \\
C(2, 1) =
\begin{cases}
C(1, 0) = 1\\
+ \\
C(1, 1) = 1
\end{cases}
\end{cases} \\
+ \\
C(3, 2) =
\begin{cases}
C(2, 1) =
\begin{cases}
C(1, 0) = 1\\
+ \\
C(1, 1) = 1\\
\end{cases} \\
+ \\
C(2, 2) = 1
\end{cases}
\end{cases}
- 所以答案為6。
- 你會發現一件事情，在分析的時候，有些遞迴會重複，這個時候用之前算過的值就好了。
- 例如C(2, 1)有算過兩次，第二次直接看第一次算的值(=2)就好了。
- 沒道理我們可以省略，
程式省略不了啊？
什麼是記憶化？
Memoization 記憶化 - 1
- 就是把以前算過的答案，丟在陣列記起來。
如果下次用到的時候直接給答案，不要再重算了！ - 記在哪裡？全域變數就可以啦！
- 舉個例子，記憶化的斐波那契數列會長的像右下角這樣：
- 用visit陣列來表示有沒有算過。
- 用DP陣列紀錄答案。
-
所以，實作的時候，如果遞迴時發現...
- 曾經算過(visit = true)：
- 直接回傳紀錄的答案。
- 沒算過(visit = false)：
- 遞迴算答案，紀錄起來，並標示算過。
- 曾經算過(visit = true)：
Memorization
bool visit[MAXN]; int DP[MAXN]; int f(int n){ if(n == 1 || n == 2) return 1; else if (visit[n]) return DP[n]; else { visit[n] = true; DP[n] = f(n-1) + f(n-2); return DP[n]; } }
- MAXN表示最大的N，是個常數。
更複雜一點記憶化 - C(n, m)
Memorzation 記憶化 - 2
- 在有兩個參數的遞迴中，記憶化也是可以使用的！
- 舉例來說，C(n, m)的記憶化會長的像下面這樣：
- 有沒有覺得記憶化的招數都一樣啊？ 還真的都一樣。
Memoization
bool visit[MAXN][MAXM]; int DP[MAXN][MAXM]; int C(int n, int m){ if(n == 0 || n == m) return 1; else if (visit[n][m]) return DP[n][m]; else { // visit[n][m] == false visit[n][m] = true; DP[n][m] = C(n-1, m-1) + C(n-1, m); return DP[n][m]; } }
- MAXN，MAXM表示
最大的N和最大的M，
是個常數。
自己實作記憶化！ - 彩帶問題
Memoization 記憶化 - 3
- 那麼，你會把彩帶問題的遞迴記憶化嗎？
Memoization
// RED = 0, ORANGE = 1, BLUE = 2 long long rec(int n, int type) { if (n == 1) return 1; else if (type == RED) return rec(n-1, BLUE); else if (type == BLUE) return rec(n-1, ORANGE) + rec(n-1, BLUE) + rec(n-1, RED); else if (type == ORANGE) return rec(n-1, BLUE) + rec(n-1, RED); else // Should not reach here. return 0; }
5 mins
自己實作記憶化！ - 彩帶問題
Memoization 記憶化 - 4
- 那麼，你會把彩帶問題的遞迴記憶化嗎？
Memoization
// RED = 0, ORANGE = 1, BLUE = 2 bool visit[MAXN][MAXTYPE]; long long DP[MAXN][MAXTYPE]; long long rec(int n, int type) { if (n == 1) return 1; else if (visit[n][type]) return DP[n][type]; else if (type == RED) DP[n][type] = rec(n-1, BLUE); else if (type == BLUE) DP[n][type] = rec(n-1, ORANGE) + rec(n-1, BLUE) + rec(n-1, RED); else if (type == ORANGE) DP[n][type] = rec(n-1, BLUE) + rec(n-1, RED); else // Should not reach here. return 0; visit[n][type] = true; return DP[n][type]; }
5 mins
Euclidean Algorithm
輾轉相除法
我們先來想想看...
Euclidean Algorithm 輾轉相除法 - 0
- 怎麼算出GCD(5, 12)呢?
最大公因數
5=5 12=22×3
5 = 5 \, \, \, \, \, \, \, \, \,\ \, \, \, \, \, \\
12 = 2^2 \times 3
- 因式分解後找相同，但有沒有更快的方法呢?
- 兩個數字一直互減，就會減到剩下最大公因數。
(另一個就會變成是0)
輾轉相除法的基本算法 & 小小驗證
Euclidean Algorithm
- 兩個數字一直互減，就會減到剩下最大公因數。
(另一個就會變成是0)
GCD(a,b)=GCD(a,b−a)
GCD(a, b) = GCD(a, b-a)
- 如果 ，那麼下面這個式子成立
b≥a
b \ge a
- 如果 是 的公因數，令 。
a=a′d,b=b′d
a = a'd, b = b'd
d
d
a,b
a, b
d
d
- 你會發現 也同時會是 和 的公因數。
Euclidean Algorithm 輾轉相除法 - 1
b−a
b-a
a
a
輾轉相除法的基本算法 & 小小驗證
Euclidean Algorithm
GCD(a,b)=GCD(a,b−a)
GCD(a, b) = GCD(a, b-a)
- 如果 ，那麼下面這個式子成立。
b≥a
b \ge a
GCD(a,b)=GCD(a,b%a)
GCD(a, b) = GCD(a, b\%a)
- 那麼下面也會成立。(因為%就是減到不能再減。)
- 如果說已經減到其中一個為0呢?
GCD(a,b)=a+b
GCD(a, b) = a+b
GCD(a,b)=GCD(a%b,b)
GCD(a, b) = GCD(a\%b, b)
- 同理， ，那麼下面式子也會成立。
b≤a
b \le a
- 到這裡，你會寫輾轉相除法了嗎?
Euclidean Algorithm 輾轉相除法 - 2
輾轉相除法的程式實作
Euclidean Algorithm
GCD(a,b)=GCD(a,b%a)
GCD(a, b) = GCD(a, b\%a)
- 如果 ，那麼下面這個式子成立。
b≥a
b \ge a
GCD(a,b)=a+b
GCD(a, b) = a+b
GCD(a,b)=GCD(a%b,b)
GCD(a, b) = GCD(a\%b, b)
- 同理， ，那麼下面式子也會成立。
b≤a
b \le a
int GCD(int a, int b){ if(a == 0 || b == 0) return a + b; if (b >= a) return GCD(a, b % a); else return GCD(a % b, b); }
GCD的小小程式
Euclidean Algorithm 輾轉相除法 - 3
- 如果說已經減到其中一個為0呢?
輾轉相除法的更簡單程式實作
Euclidean Algorithm
- 其實GCD可以寫成右上角的小小小小程式。
- 為什麼？我們來想想看：
- 如果a比b大，GCD(a, b)=GCD(b, a%b)
- 如果b比a大，GCD(a, b)=GCD(b, a%b)=GCD(b, a)
-
你發現了嗎? 不管a,b大小怎麼樣，下一次遞迴呼叫後，比較大的數字都會在前面。
- 如果a比b大， b > a%b。
- 如果b比a大，b > a。
- 所以，只要移動一下下一次遞迴的參數位置，就可以確保比較大的都在前面。
- 為什麼？我們來想想看：
int GCD(int a, int b){ if(a == 0 || b == 0) return a + b; if (b >= a) return GCD(a, b % a); else return GCD(a % b, b); }
GCD的小小程式
int GCD(int a, int b){ if(a * b == 0) return a + b; return GCD(b, a % b); }
GCD的小小小小程式
Euclidean Algorithm 輾轉相除法 - 4
Exercise III
Rhythm Doctor - 最大公因數的應用問題
Exercise III
程式練習題
接下來有一題請你用程式實做遞迴的應用題。
- 我會花1分鐘讀題。
- 總共計時10分鐘。
- 計時之前，好好複習一下GCD的程式。
229 - Rhythm Doctor - 工商
Exercise III - Rhythm Doctor - 0
- 分享一個 Rhythm Doctor 我最喜歡的一首。
10 mins
229 - Rhythm Doctor - 題目
- 題目：每個人的生命中都有各自的拍數。假設大家的拍子都從第1秒開始，
請問下一次大家剛好在同個時間打拍子是什麼時候？
(保證答案在long long範圍內。)
- 舉例來說，如果有兩個人AB，A和B的拍數分別為3和4，
那麼下次同時打拍子會在第12秒。
10 mins
Exercise III - Rhythm Doctor - 1
A
B
3s
3s
3s
3s
4s
4s
4s
229 - Rhythm Doctor - 解析
- 題目：每個人的生命中都有各自的拍數。假設大家的拍子都從第1秒開始，
請問下一次大家剛好在同個時間打拍子是什麼時候？
(保證答案在long long範圍內。)
- ㄚ就是多個數字的LCM(最小公倍數) 啊？
- 記得要把code改成long long。
10 mins
Exercise III - Rhythm Doctor - 2
long long GCD(long a, long b){ if(a * b == 0) return a + b; return GCD(b, a % b); }
long long LCM(long long a, long long b){ return a / GCD(a, b) * b; }
229 - Rhythm Doctor - 解析
- 題目：每個人的生命中都有各自的拍數。假設大家的拍子都從第1秒開始，
請問下一次大家剛好在同個時間打拍子是什麼時候？
(保證答案在long long範圍內。)
- ㄚ就是多個數字的LCM(最小公倍數) 啊？
- 就一直拿數字做LCM就好了。
10 mins
Exercise III - Rhythm Doctor - 3
int main() { long long n, ans = 1, x; cin >> n; for (int i=0; i<n; i++) { cin >> x; ans = LCM(ans, x); } cout << ans << endl; }
Exercise IV
零和問題 - 暴力搜尋所有可能
Exercise IV
程式練習題
接下來有一題請你用程式實做遞迴的應用題。
- 我會花1分鐘讀題。
- 總共計時10分鐘。
- 這題很不簡單，不寫出來沒關係，但先想想看你要怎麼寫以及遞迴的過程。
228 - 零和問題 - 題目
Exercise IV - Subset Sum Problem 零和問題 - 0
> 20 mins
- 題目：現在有n個正整數，請問你可不可以從中間選幾個數字使其加總為k？
如果可以輸出"YES"，否則輸出"NO"。(如果數字選過了就不能再選了。)
- 舉例來說，如果有五個數字[3, 7, 11, 9, 4]，請問可不可以湊到數字16呢？
- 輸出YES，因為 7 + 9 = 16。
- 好像很難也？Hint: 我們來畫畫看這題的遞迴樹。
228 - 零和問題 - 提示
> 20 mins
- 題目：現在有n個正整數，請問你可不可以從中間選幾個數字使其加總為k？
如果可以輸出"YES"，否則輸出"NO"。(如果數字選過了就不能再選了。)
(0, 0)
(1, 3)
(1, 0)
(2, 10)
(2, 7)
(2, 3)
(2, 0)
(3, 21)
(3, 14)
(3, 10)
(3, 3)
(4, 30)
(4, 19)
(4, 21)
(4, 10)
(5, 34)
(5, 25)
(5, 30)
(5, 21)
前
四
種
可
能
(看第幾個數字，
現在加到哪裡)
選
不選
+3
+7
+7
+11
+11
+9
+9
+4
+4
- 舉例來說，如果有五個數字[3, 7, 11, 9, 4]，請問可不可以湊到數字16呢？
Exercise IV - Subset Sum Problem 零和問題 - 1
228 - 零和問題 - 引導
> 20 mins
- 題目：現在有n個正整數，請問你可不可以從中間選幾個數字使其加總為k？
如果可以輸出"YES"，否則輸出"NO"。(如果數字選過了就不能再選了。)
- 根據我們所寫的遞迴樹，我們會知道怎麼暴力搜尋。
- 一開始看第0個，接下來我們分成兩個case來看：
- 選第0個數字 (3)，接下來看第1個數字，分成兩個case來看：
- 選第1個數字 (10)，接下來看第2個數字，分成兩個case來看...
- 不選第1個數字 (3)，接下來看第2個數字，分成兩個case來看...
-
不選第0個數字 (0)，接下來看第1個數字，分成兩個case來看：
- 選第1個數字 (7)，接下來看第2個數字，分成兩個case來看...
- ....
- 選第0個數字 (3)，接下來看第1個數字，分成兩個case來看：
- 一開始看第0個，接下來我們分成兩個case來看：
- 舉例來說，如果有五個數字[3, 7, 11, 9, 4]，請問可不可以湊到數字16呢？
Exercise IV - Subset Sum Problem 零和問題 - 2
228 - 零和問題 - 引導
> 20 mins
- 題目：現在有n個正整數，請問你可不可以從中間選幾個數字使其加總為k？
如果可以輸出"YES"，否則輸出"NO"。(如果數字選過了就不能再選了。)
- 遞迴參數：現在看到第幾個數字 i，以及現在總和 S。
- 要暴搜rec(i, S)的所有可能，可以分成兩個case暴搜：
- 選第i個數字：rec(i+1, S+A[i])
- 不選第i個數字：rec(i+1, S)
- 終止條件？
- 所有數字都看完了。
- i = n。
- 所有數字都看完了。
- 要暴搜rec(i, S)的所有可能，可以分成兩個case暴搜：
Exercise IV - Subset Sum Problem 零和問題 - 3
228 - 零和問題 - 解答
> 20 mins
- 題目：現在有n個正整數，請問你可不可以從中間選幾個數字使其加總為k？
如果可以輸出"YES"，否則輸出"NO"。(如果數字選過了就不能再選了。)
bool rec (int i, int S) { if (i == n) return S == k; else return rec(i+1, S+A[i]) || rec(i+1, S); }
- 遞迴參數：現在看到第幾個數字 i，以及現在總和 S。
- 要暴搜rec(i, S)的所有可能，可以分成兩個case暴搜：
- 選第i個數字：rec(i+1, S+A[i]) / 不選第i個數字：rec(i+1, S)
- 終止條件？所有數字都看完了，也就是i = n。
- 要暴搜rec(i, S)的所有可能，可以分成兩個case暴搜：
Exercise IV - Subset Sum Problem 零和問題 - 4
228 - 零和問題 - 比較詳細的解答
> 20 mins
#include <iostream> #define MAXN 30 using namespace std; int k, A[MAXN], n; bool rec (int i, int S) { if (i == n) return S == k; else return rec(i+1, S+A[i]) || rec(i+1, S); } int main () { cin >> n >> k; for (int i=0; i<n; i++) cin >> A[i]; cout << (rec(0, 0) ? "YES" : "NO") << endl; }
- 題目：現在有n個正整數，請問你可不可以從中間選幾個數字使其加總為k？
如果可以輸出"YES"，否則輸出"NO"。(如果數字選過了就不能再選了。)
Exercise IV - Subset Sum Problem 零和問題 - 5
Pruning
剪枝
什麼是剪枝？
Pruning 剪枝 - 1
- 就是不要讓遞迴跑的太多次！
- 簡單來說，如果接下來一定不會找到答案，我們就別再找下去了，
直接停掉避免浪費時間。 - 在遞迴樹上砍掉一些點 → 所以這個技巧被稱作剪枝(Pruning)。
- 簡單來說，如果接下來一定不會找到答案，我們就別再找下去了，
Pruning
在零和問題剪枝？
- 來看看剛剛遞迴樹怎麼剪枝吧!
Pruning
Pruning 剪枝 - 2
- 舉例來說，如果有五個數字[3, 7, 11, 9, 4]，請問可不可以湊到數字16呢？
- 把不可能的遞迴跳掉！
(0, 0)
(1, 3)
(1, 0)
(2, 10)
(2, 7)
(2, 3)
(2, 0)
(3, 21)
(3, 14)
(3, 10)
(3, 3)
(4, 19)
(4, 10)
(5, 25)
(5, 10)
(看第幾個數字，
現在加到哪裡)
選
不選
+3
+7
+7
+11
+11
+9
+4
(4, 23)
(4, 14)
+9
(5, 19)
(5, 14)
+4
在零和問題剪枝？
- 把不可能的遞迴跳掉！
- 還可以減掉更多枝嗎？
- 如果題目數字有可能是負數，還可以這樣做嗎？
Pruning
Pruning 剪枝 - 2
bool rec (int i, int S) { if (S > k) return false; if (i == n) return S == k; else return rec(i+1, S+A[i]) || rec(i+1, S); }
Talks
關於遞迴的小小雜談
題目表 - 遞迴
題目表 - 0
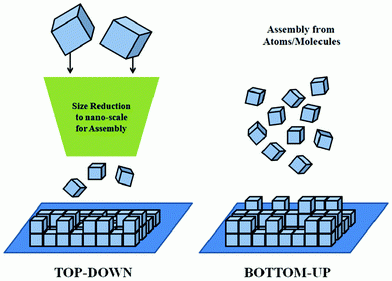
Top-down & Bottom-up
Talks - 1
- 其實你隱約知道了，有些遞迴是可以用for迴圈寫的。
- 我們來複習用for迴圈實作斐波那契數列？
- 你會發現，用for迴圈通常都是慢慢堆答案上去的，
- 這類的方法稱作Bottom-up，也就是堆上去的方法。
- 那麼遞迴呢？通常遞迴都是從大問題去呼叫小問題的，
這類的方法稱作為Top-down。
- 「遞迴只應天上有，凡人應當用迴圈」
int fib[100] = {0, 1, 1}; for (int i=3; i<=n; i++) { fib[i] = fib[i-1] + fib[i-2]; }
Talks - 2
- 想要知道Top-down & Bottom-up的後續嗎？
- 去看看算法班的動態規劃 DP (Dynamic Programming)吧！ (蛋餅的投影片)
- 但並不是所有題目都適合用Bottom-up，所以還是要會遞迴喔~
Top-down & Bottom-up
更多的遞迴...
Talks - 3
- 其實最後一個問題 - 零和問題對初心者來說很難啦，
所以可以回去在複習一次OuO。 - 雖然零和問題很難，但是這才是遞迴的剛開始而已！
- 如果你對遞迴很有興趣，歡迎參考我在資訊之芽的遞迴講義，
- 這個講義有四分之一我們剛剛講過了，
但後半段比我們這堂課還要難很多喔！ 例如我們有提及...- 河內塔
- 字串枚舉
- 數獨
- 搶數字問題
- 這個講義有四分之一我們剛剛講過了，
- 這是我們最後一堂課了QQ，祝你們明天模擬考順利！
End
Q&A?
其實...
Talks - 0
- 在APCS實作題裡面，其實幾乎沒有裸遞迴題。
- 但是遞迴非常的重要！
- 在算法班的課程裡，除了資料結構 / 貪心以外，一定會用到遞迴
(其他不是用不到，也可能會用到遞迴) - 遞迴的概念對新手來說很不好理解，要慢慢適應遞迴的思考方法。
Recursion Arvin Liu
APCS camp - Recursion
By Arvin Liu
APCS camp - Recursion
APCS Camp Recursion
- 1,633
