Optimization-based Planning Through Contact with Tight Convex Relaxations
1X Robotics, August 2023
Bernhard Paus Græsdal
Robot Locomotion Group, MIT
About me
- Current PhD student at RLG, MIT
- MsC in Cybernetics and Robotics from NTNU
- Research: Planning Through Contact with Convex Optimization
Robot Locomotion Group
- Led by Prof. Russ Tedrake
- Focused on robot locomotion for many years
- Tools from optimization, control and machine learning
- Today focused on Robotic Manipulation
- Lmk if you want to visit!
Planning Through Contact
Dexterous Manipulation: How to pick up the book?
Planning Through Contact
Complex planning problem:
- 4 contact bodies
(table, book, two fingers) - 4 different contact modes
- Both pushing and sticking
- Collision-free motion planning
Dexterous Manipulation: How to pick up the book?
How are these problems solved today?
Task-specific hardware
\( \rightarrow \) Not dexterous manipulation
How are these problems solved?
Learning-based methods
\( \rightarrow \) Hard to generalize
- Sampling-based
- Task-and-Motion-Planning (TAMP)
(often sampling-based) - Multi-Modal Motion Planning (MMMP)
Planning algorithms:
How are these problems solved?
[1] T. Pang, H. J. T. Suh, L. Yang, and R. Tedrake, “Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models.” arXiv, Jun. 21, 2022
[1]
\( \rightarrow \) Several pros and cons
\( \rightarrow \) No known (general) satisfactory solution
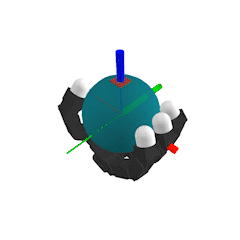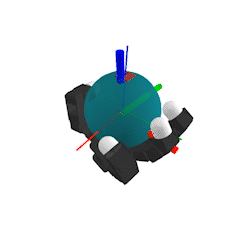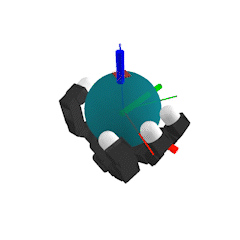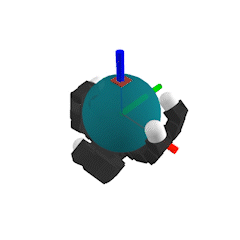
Our goal
- Optimization-based planner for dexterous manipulation
- Plan both discrete contact mode sequence and continuous motion simultaneously
\(\leftarrow\) Toy-problem we will tackle
Preliminary results: Planar Pushing
Technical Approach
Characteristics of the problem:
- Hybrid system
- Nonlinear kinematics and dynamics
- (we use planar pushing here as an example; generalizes to general rigid body dexterous manipulation!)
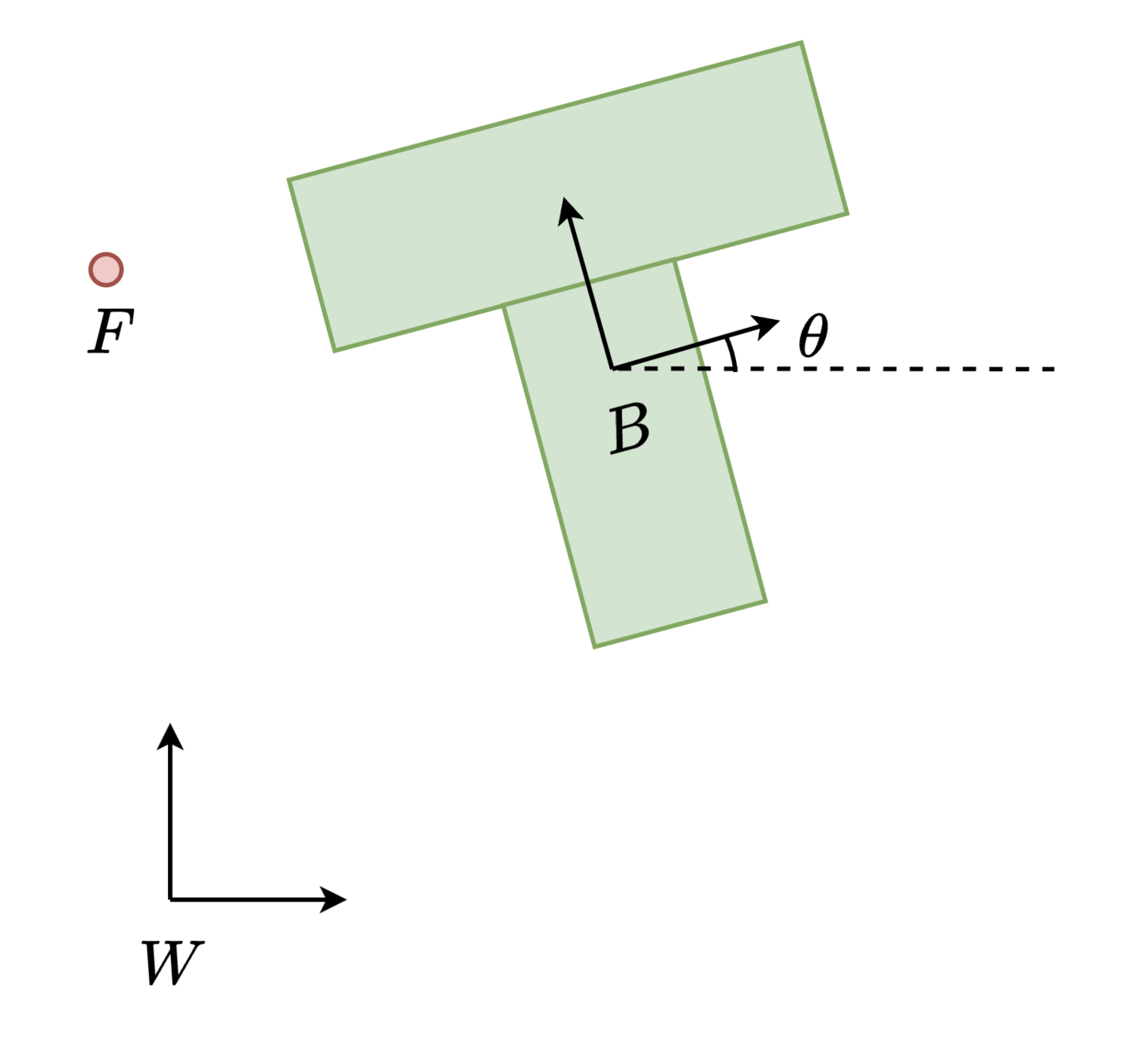
Technical Approach
- Hybridness
- Solve using convex (linear) Mixed-Integer relaxations
- Nonlinearities
- Solve using convex (semidefinite) programming relaxations
- We propose to use convex optimization and tight convex relaxations to solve the problem!
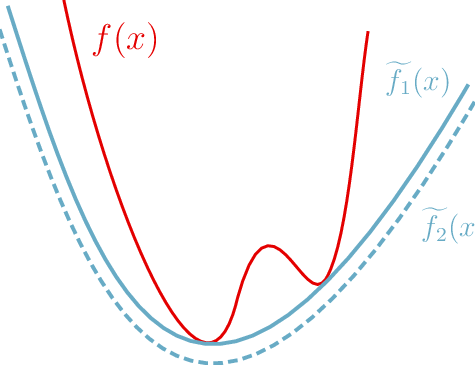
\( \tilde{f}_1 \) and \(\tilde{f}_2\) are simple examples of convex relaxations
1. Hybridness of the problem
- Combinatorial problems can be solved with MICP
- (generally) NP-hard
- Formulate the problem as
Graph-of-Convex-Sets (GCS) problem- 1. Efficient encoding, fewer integer variables
- 2. Tight convex relaxation
\( \rightarrow \) we can solve it fast! - (Round to obtain true solution)
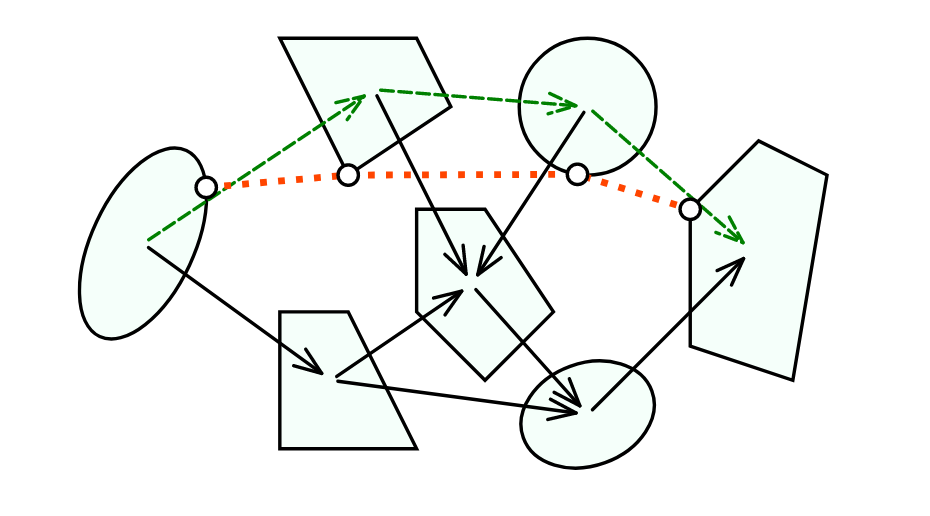
[2] T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” arXiv, Sep. 21, 2022.
[3] T. Marcucci, M. Petersen, D. von Wrangel, and R. Tedrake, “Motion Planning around Obstacles with Convex Optimization.” arXiv, May 09, 2022.
[2]
Graph of Convex Sets (GCS)
[2] T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” arXiv, Sep. 21, 2022.
[3] T. Marcucci, M. Petersen, D. von Wrangel, and R. Tedrake, “Motion Planning around Obstacles with Convex Optimization.” arXiv, May 09, 2022.
[2]
TODO add Mark video!
Graph-of-Convex-Sets
- Directed graph \( G = (\mathcal{V}, \mathcal{E}) \)
- Bounded convex sets \( \mathcal{X}_v \)
- Source and target \( \sigma, \tau \in \mathcal{V} \)
- \( \mathcal{P} \) family of all \( \sigma-\tau \) paths in \( G \)
- \( \mathcal{E}_p \) set of edges traversed by path \( p \in P \)
- Convex edge lengths \( l_e(x_u, x_v) \geq 0 \)
- Convex edge constraints \( \mathcal{X}_e \)
\begin{aligned}
\min \quad& \sum_{e := (u,v) \in \mathcal{E}_p} l_e(x_u, x_v) \\
\text{s.t.} \quad&
p \in \mathcal{P}, \\
\quad & x_v \in \mathcal{X}_v, \quad \forall x_v \in p, \\
\quad & (x_u, x_v) \in \mathcal{X}_e, \quad \forall e := (x_u, x_v) \in \mathcal{E}_p
\end{aligned}
[1] T. Marcucci, J. Umenberger, P. A. Parrilo, and R. Tedrake, “Shortest Paths in Graphs of Convex Sets.” 2022.
[2] T. Marcucci, M. Petersen, D. von Wrangel, and R. Tedrake, “Motion Planning around Obstacles with Convex Optimization.” 2022.
2. Handling nonlinearities
- Constraints are polynomial
- Problem can be formulated as a (non-convex) QCQP
- Can be relaxed to a Semidefinite Program (SDP)
- Convex and can be solved efficiently!
- (round to obtain true solution)
2. Handling nonlinearities
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
- A general non-convex QCQP:
- (any polynomial problem can be put in this form)
2. Handling nonlinearities
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
- We solve it with the standard SDP relaxation
\begin{aligned}
\min_{x} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\
\quad
AXA^\intercal &\geq 0 \\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
e_1^\intercal X e_1 &= 1 \\
\quad
X \succeq 0 \\
\end{aligned}
\( \longrightarrow \)
- Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
- (This includes the McCormick envelopes/outer-approximation of bilinear constraints)
\( X := xx^\intercal \)
2. Handling nonlinearities
- Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
- Usually not the case
- Relaxation close to being tight
- Round using nonlinear trajopt and fixed mode-sequence
Hope: Convex relaxation contains enough information to take the right high-level decisions
Seems to be the case!
Preliminary Results
Pushing for the T-object
General 2D dexterous manipulation
-
The method generalizes to general dexterous manipulation!
Future work
- Pushing for ICRA 2023 with paper on complete motion planning for planar pushing
- Execute trajectories on the real robot (with hybrid MPC as controller)
- General 3D dexterous manipulation for general rigid objects
Thank you!
Optimization-based Planning Through Contact with Tight Convex Relaxations
By Bernhard Paus Græsdal
