Planning Through Contact with Graphs of Convex Sets and Semidefinite Relaxations
Bernhard Paus Græsdal
Robot Locomotion Group, MIT
1X Robotics
August 11th 2023
About me
- Current PhD student at RLG, MIT
- Research: Planning Through Contact with Convex Optimization
Bernhard Paus Græsdal
Robot Locomotion Group
- Led by Prof. Russ Tedrake
- Focused on robot locomotion for many years
- Tools from optimization, control and machine learning
- ~20% of former members now work for BD
- Today focused on Robotic Manipulation
- Lmk if you want to visit!
Planning and control for complex robotic systems
A big focus for the group:
Goal: Deeper connections between
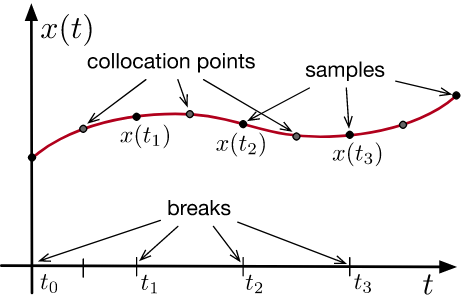
Trajectory optimization
Sample-based planning
AI-style logical planning
Combinatorial optimization
Shortest Paths in Graphs of Convex Sets.
Tobia Marcucci, Jack Umenberger, Pablo Parrilo, Russ Tedrake.
Available at: https://arxiv.org/abs/2101.11565
Motion Planning around Obstacles with Convex Optimization.
Tobia Marcucci, Mark Petersen, David von Wrangel, Russ Tedrake.
Available at: https://arxiv.org/abs/2205.04422
Simple example: Shortest path around an obstacle
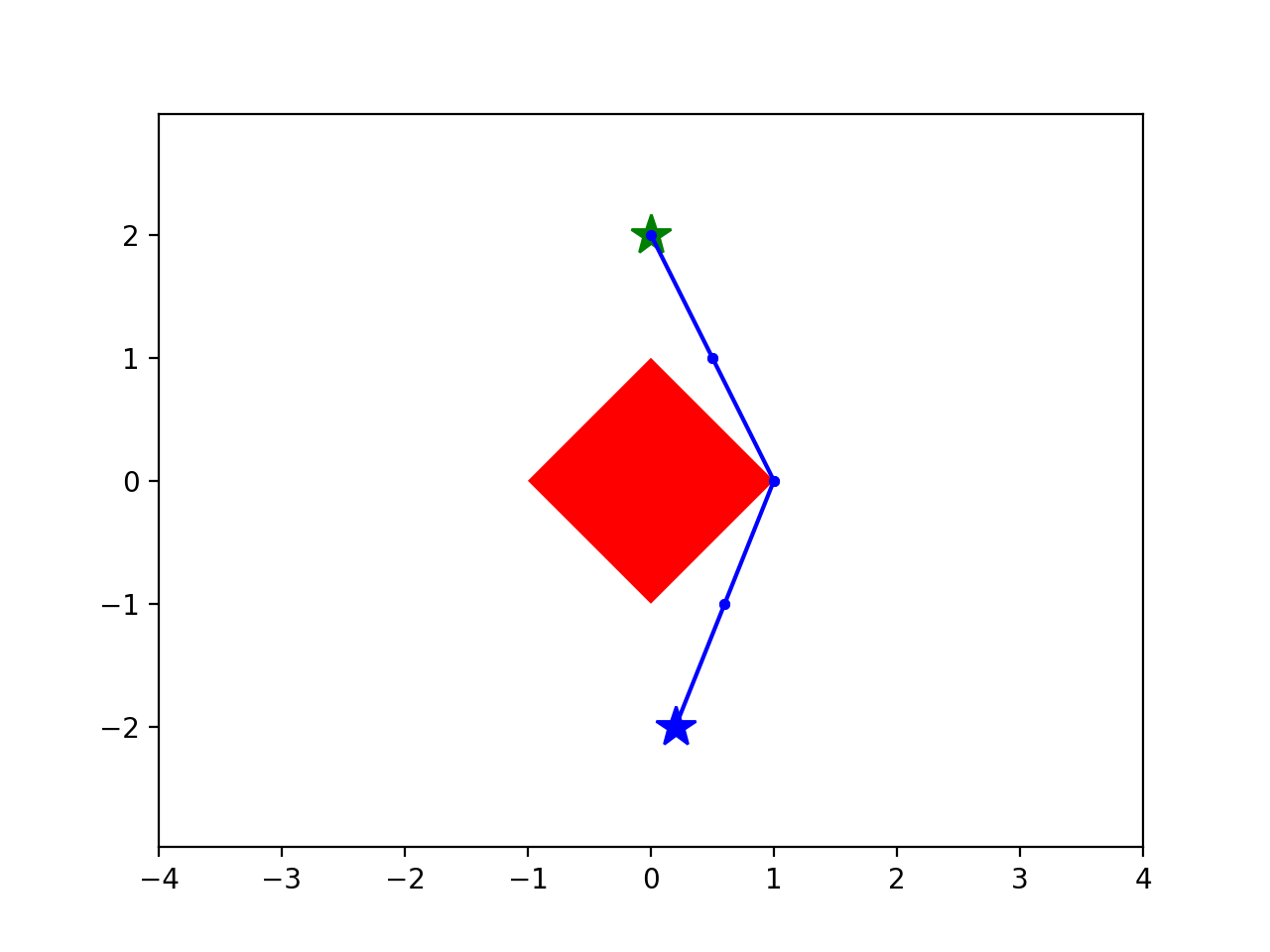
start
goal
- Combinatorial (e.g. over homotopy classes)
- Smooth optimization (over curves)
Two aspects of the motion planning problem:
start
goal
- How to do trajectory optimization through the maze?
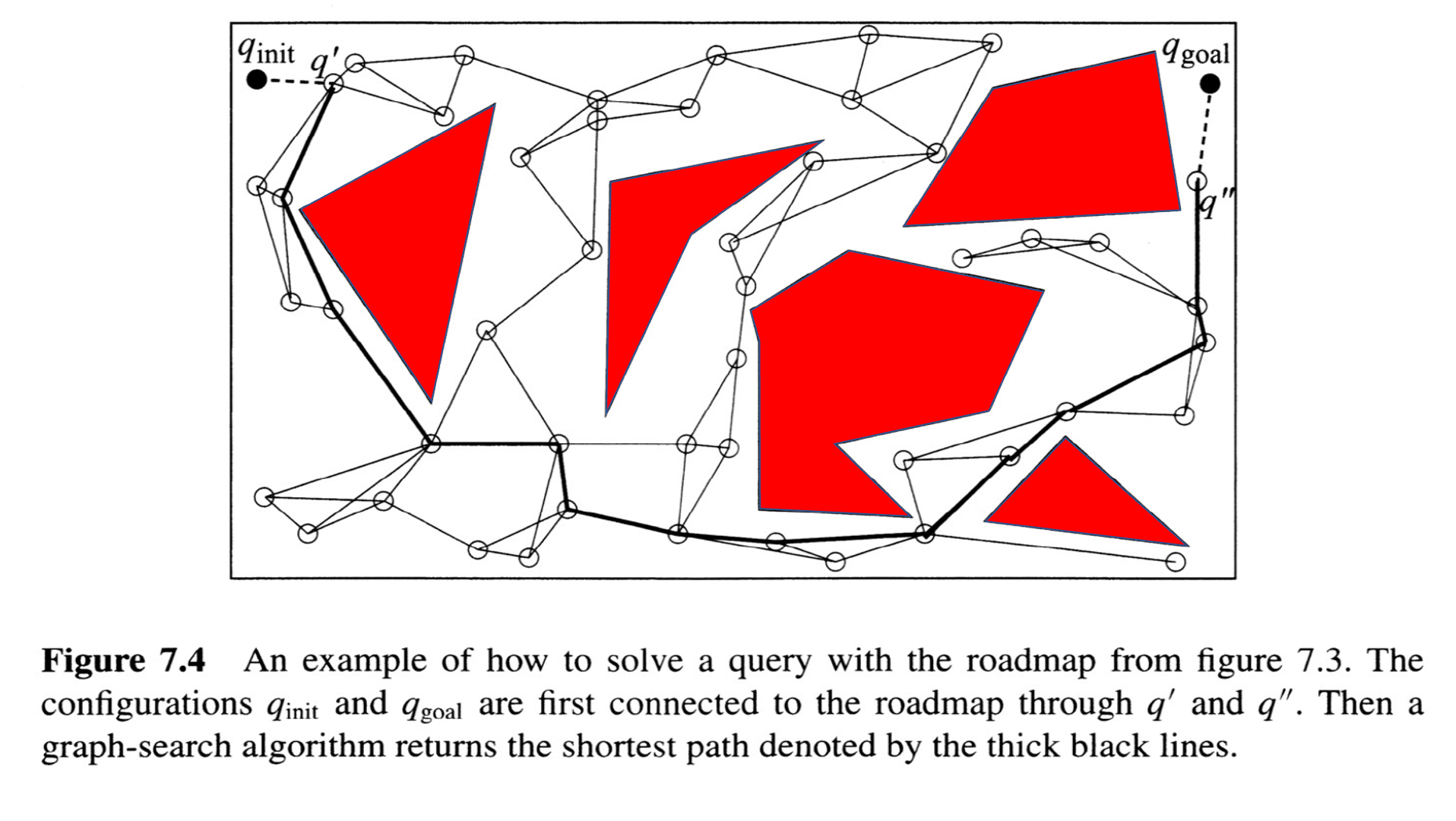
1. Combinatorial: Sampling-based motion planning
The Probabilistic Roadmap (PRM)
from Choset, Howie M., et al. Principles of robot motion: theory, algorithms, and implementation. MIT press, 2005.
2. Smooth: Trajectory Optimization
- Vertices \(V\)
- (Directed) edges \(E\)
Combining Graph Search + Trajectory Optimization
- Start with classical Linear Programming (LP) formulation of SPP
Graphs of Convex Sets
-
For each \(i \in V:\)
- Compact convex set \(X_i \subset \R^d\)
- A point \(x_i \in X_i \)
- Edge length given by a convex function \[ \ell(x_i, x_j) \]
Note: The blue regions are not obstacles.
New shortest path formulation
\begin{aligned} \min_{\varphi} \quad & \sum_{(i,j) \in E} c_{ij} \varphi_{ij} \\
\mathrm{s.t.} \quad
& \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si}, && \forall i \in V, \\
& \varphi_{ij} \geq 0, && \forall (i,j) \in E.
\end{aligned}
Classic shortest path LP
\begin{aligned} \min_{\varphi,x} \quad & \sum_{(i,j) \in E} \ell_{ij}(x_i, x_j) \varphi_{ij} \\
\mathrm{s.t.} \quad
& x_i \in X_i, && \forall i \in V, \\
& \sum_{j \in E_i^{out}} \varphi_{ij} + \delta_{ti} = \sum_{j \in E_i^{in}} \varphi_{ji} + \delta_{si} \le 1, && \forall i \in V, \\
& \varphi_{ij} \geq 0, && \forall (i,j) \in E.
\end{aligned}
now w/ Convex Sets
Example: "Footstep planning" with \(x_{n+1}=Ax_n + Bu_n\)
Formulating motion planning with differential constraints as a Graph of Convex Sets (GCS)
+ time-rescaling
Motion Planning Results
minimum distance
minimum time
Back to the maze example...
Previous formulations were intractable; would have required \( 6.25 \times 10^6\) binaries.
Scaling
-
~10k regions in 3D
-
20k vertices and 400k edges.
- Online planning takes 0.3s
by Tobia Marcucci in collaboration w/ Stephen Boyd
Going beyond collision-free motion planning...
How to pick up the book?
Planning Through Contact
- 4 contact bodies
(table, book, two fingers) - Many different contact modes
- Both sliding and sticking
- Collision-free motion planning
Complex planning problem:
How to push the object?
Planning Through Contact
C. Chi et al., “Diffusion Policy: Visuomotor Policy Learning via Action Diffusion.” arXiv, Mar. 09, 2023
- No satisfactory planning algorithm for this problem!
Characteristics of the problem:
- Hybrid system
- Nonlinear kinematics and dynamics
Using GCS for Planning Through Contact
\(\rightarrow \) Solve hybridness by using GCS
Nonlinearities and convex relaxations
- Solve nonlinearities by using convex (semidefinite) programming relaxations
- We propose to use convex optimization and tight convex relaxations to solve the problem!
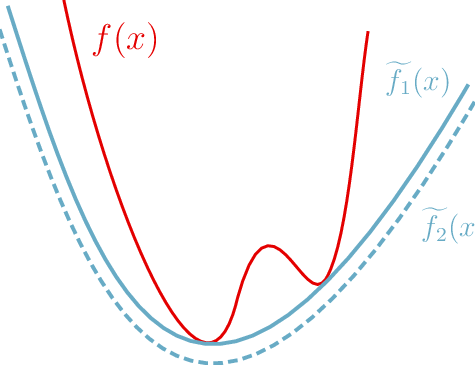
\( \tilde{f}_1 \) and \(\tilde{f}_2\) are simple examples of convex relaxations
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
- A general non-convex QCQP:
- (any polynomial problem can be put in this form)
Formulate the problem as a QCQP
- (any polynomial problem can be put in this form)
Non-convex when \( Q_i \preceq 0 \)
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
\begin{aligned}
\min_{x} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\
\quad
AXA^\intercal &\geq 0 \\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
e_1^\intercal X e_1 &= 1 \\
\quad
X \succeq 0 \\
\end{aligned}
\( \longrightarrow \)
- Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
- (This includes the McCormick envelopes/outer-approximation of bilinear constraints)
\( X := xx^\intercal \)
Solve it using Semidefinite Programming (SDP)
- Exact when \( \text{rank}(X) = 1 \iff X = x x^\intercal \) \( \rightarrow\) relaxation is "tight"
- In general not the case (otherwise \( P = NP \) )
- Depending on the problem, relaxation can be tight
- Hope: Convex relaxation contains enough information to take the correct high-level decisions
- Then we can refine the details as a final step!
Retrieve the solution
Preliminary results on using GCS and Semidefinite relaxations for planning through contact...
Planning through contact for Planar Pushing
Planning through contact for general manipulation
- Pushing for ICRA 2023 with paper on first results
- Next step: General 3D dexterous manipulation for general rigid objects
Future work
Thank you!
Planning Through Contact with Graphs of Convex Sets and Semidefinite Relaxations
By Bernhard Paus Græsdal
