Contact-rich planning without mode enumeration
Short Talk, RLG MIT
February 23rd 2024
Bernhard Paus Graesdal
Preliminary work:
Motivation
- Use GCS for contact-rich planning
- Currently contact modes are encoded explicitly in graph
- An obstacle is scaling
- Contact mode enumeration scales exponentially with number of bodies in a scene
Example
- A box on a table with a point finger
- We model three contact points:
- Table and box bottom left corner, Table and box bottom right corner, finger and box left face
- Consider 4 modes:
- Non-contact, sticking contact, sliding left, sliding right
- We get \(4^3 = 64\) modes = vertices in GCS
- Need \(64^2 = 4096\) edges to model arbitrary contact mode transitions!
Proposed solution
- Describe contact modes implicitly using Linear Complimentarity Constraints (LCPs)
- LCPs can be encoded as linear inequality and quadratic equality constraints
- Use Semidefinite Relaxations to relax the feasible set
- Solve a convex program to obtain a lower bound/relaxed solution
- Round to obtain feasible solution
Complimentarity Constraints
- Contact modes can be encoded as Complimentarity Constraints:
\( 0 \leq f(x) \perp g(x) \geq 0, \quad f, g: \R^n \rightarrow \R^n \) - Nonnegativity implies that this must hold element-wise
- Only one expression can be positive at a time:
- \( f_i(x) = 0 \) and \( g_i(x) \geq 0 \)
- \( f_i(x) \geq 0 \) and \( g_i(x) = 0 \)
- We obtain an LCP when \(f\) and \(g\) are linear:
\( 0 \leq Ax + b \perp Cx + d \geq 0 \) - Which we can encode with linear and quadratic constraints
Example: Contact/Non-contact
- Two modes: Contact or non-contact
- Let \( \phi : \R^n \rightarrow \R\) be SDF and let \( \lambda_n \in \R \) be normal force
- Contact: \(\phi(q) = 0 \) and \(\lambda_n \geq 0\)
- Non-contact: \(\phi(q) \geq 0 \) and \(\lambda_n = 0\)
Example: Contact/Non-contact
0 \leq \phi(q) \perp \lambda_n \geq 0
- Suppose \(\phi\) is linear (i.e. by approximation)
- Then the LCP is obviously:
Example: Sliding/Sticking
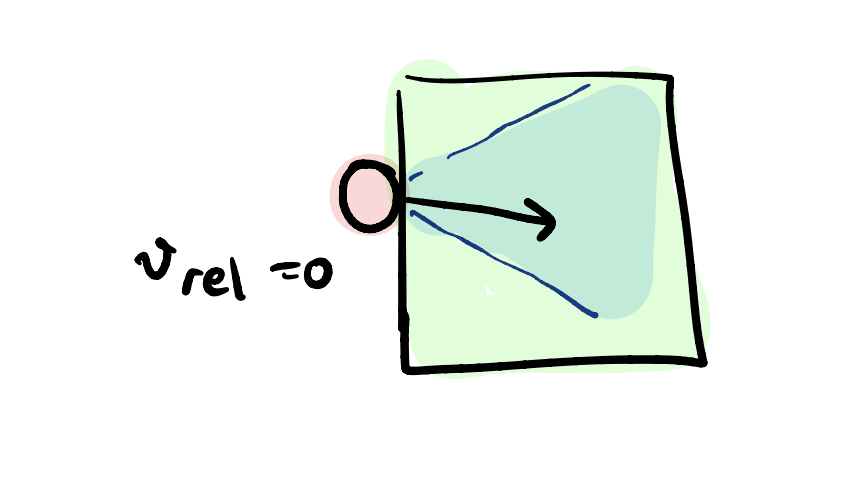
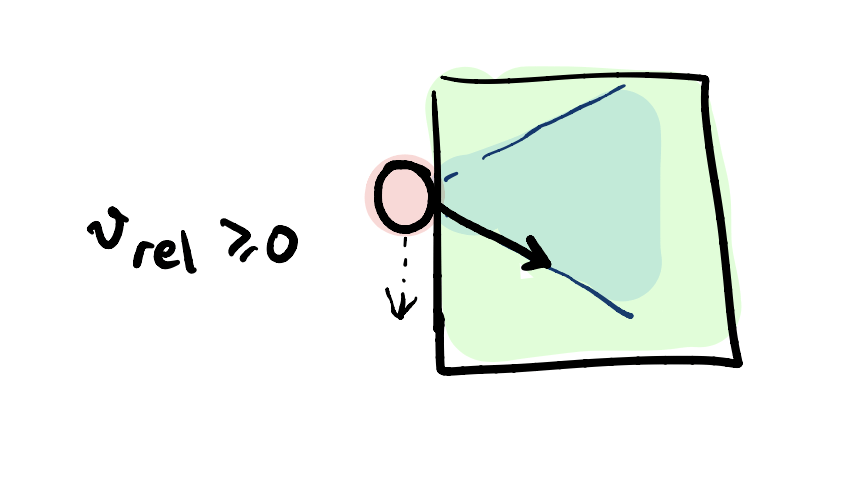
- Two modes: Sliding or Sticking (in 2D)
- \( \lambda_f \in \R \) is the friction force, \( v_{\text{rel}} \in \R \) is the relative sliding velocity
Sticking: \( | \lambda_f | \leq \mu \lambda_n \) and \( v_{\text{rel}} = 0\)
Sliding: \( | \lambda_f | = \mu \lambda_n \) and \( |v_{\text{rel}} | \geq 0\)
Example: Sliding/Sticking
- How to encode as LCP?
- Introduce auxiliary friction force variables for each direction
- Introduce a slack variable \( \gamma \in \R \) for \( |v_\text{rel} | \)
Sticking: \( | \lambda_f | \leq \mu \lambda_n \) and \( v_{\text{rel}} = 0\)
Sliding: \( | \lambda_f | = \mu \lambda_n \) and \( v_{\text{rel}} \geq 0\)
\begin{aligned}
0 \leq \gamma e + v_\text{rel} &\perp \lambda_f \geq 0 \nonumber \\
0 \leq \mu \lambda_n - e^T \lambda_f &\perp \gamma \geq 0 \nonumber
\end{aligned}
e = [1, \ldots, 1]^T
- Enforces sticking/sliding constraints exactly (for polyhedral cones)
- (Other LCP approximations exist, like Anitescu, etc)
J. C. Trinkle, S. Berard, and J. S. Pang, “A time-stepping scheme for quasistatic multibody systems,” 2005 (ISAPT)
T. Pang and R. Tedrake, “A Robust Time-Stepping Scheme for Quasistatic Rigid Multibody Systems,” in 2018 (IROS)
Contact in 2D
\begin{align}
0 \leq \phi(q) &\perp \lambda_n \geq 0 \quad \quad \\
0 \leq \gamma e + v_\text{rel} &\perp \lambda_f \geq 0 \\
0 \leq \mu \lambda_n - e^T \lambda_f &\perp \gamma \geq 0
\end{align}
e = [1, \ldots, 1]^T
- We can describe contact/non-contact and sliding/sticking with the LCPs:
J. C. Trinkle, S. Berard, and J. S. Pang, “A time-stepping scheme for quasistatic multibody systems,” 2005 (ISAPT)
T. Pang and R. Tedrake, “A Robust Time-Stepping Scheme for Quasistatic Rigid Multibody Systems,” in 2018 (IROS)
Motion Planning in 2D
- We formulate the motion planning problem:
- Assume quasi-static dynamics
- Discretize using Backward Euler
- Decision variables:
\((p_k, \theta_k) \in \text{SE}(2), \, \lambda_{n,k}, \lambda_{f,k} \in \R^2, \, k = 0, \ldots, N-1\) - Parametrize \( \theta \) by \( c_\theta, s_\theta \in \R \)
- Bilinear expressions:
- LCP constraints
- Cross-product of arm x force
- SO(2)
- Rotation of forces
Semidefinite Relaxation
\begin{aligned}
\min_{x} \quad x^\intercal Q_0 x & \\
\text{subject to}
\quad
x^\intercal Q_i x &\geq 0, \quad \forall i = 1, \ldots \\
\quad
Ax &\geq 0 \\
\quad
x &=
\begin{bmatrix}
1 \\
y
\end{bmatrix}
\end{aligned}
Quadratic equality constraints can be formulated as:
where \(Q_i\) possibly indefinite, hence problem is nonconvex
Lift the problem:
\( x \in \R^n \rightarrow (x, X) \in \R^n \times \mathbb{S}^{n \times n}\)
\begin{aligned}
\min_{x} \quad \langle Q_0, X \rangle & \\
\text{subject to}
\quad
\langle Q_i, X \rangle &\geq 0, \quad \forall i = 1, \ldots \\
\quad
AXA^\intercal &\geq 0 \\
\quad
AXe_1^\intercal &\geq 0 \\
\quad
e_1^\intercal X e_1 &= 1 \\
\quad
X \succeq 0 \\
\end{aligned}
Equivalent when \( \text{rank}(X) = 1 \iff X = x x^\intercal \)
Otherwise a convex relaxation
\( \longrightarrow \)
\( X := xx^\intercal \)
Result: Pushing a box
Result: Pushing a box
- Three contact points:
- Finger/Box face
- Box left corner/table
- Box right corner/table
- 1. Transitions from non-contact to contact to non-contact
- 2. and 3. Transitions from sticking to sliding to sticking
Result: Box flip-up
Result: In-place box flip-up
- Some obvious constraint violation
- Seems to depend a bit on friction coeff, cost coefficients, etc.
Looks promising, but more experimentation and analysis is needed!
Conclusion:
Thoughts
- Explicitly enumerating contact modes creates "fake" combinatorics
- This idea relies on a linearization of the SDF around a point/in a region
- Idea: Use GCS to plan through multiple linearization points
- Perhaps this is closer to the "actual combinatorics" i.e. "go left/right"?
Future work
- Test more complex systems:
- Multiple point fingers
- A one/two link finger
- Exploit (band) sparsity
Thank you!
Planning Through Contact without Mode Enumeration
By Bernhard Paus Græsdal
