Educational Technologies: Conceptual model
Group 3
Kanya Paramita
Bhoomika Agarwal
April 1, 2020
Conceptual model
- Problem Definition
- Learning Objectives and Outcomes
- Learning Paradigm
- Learning Activity
- Performance Measures
- Toolings
Problem Definition
Eigen-Value Decomposition at University level
Eigen-values & Eigen-vectors??

Problem statement
Lacking in contextual and visual learning of Eigenvectors and Eigenvalues concepts
Aims of our learning framework
- Visualize the Eigenvalues and Eigenvectors and learn the concepts related to them
- Find solutions to linear algebra problems using a procedural and algorithmic approach
- Learn and retain the math principles associated with these concepts
Learning Objectives and Outcomes
Apply basic concepts of Eigenvalues and Eigenvectors
Learning objectives
- Define Eigenvalues and Eigenvectors problems
- Find Eigenvalues and Eigenvectors geometrically and numerically
- Understand Eigenvalues and Eigenvectors theorems
- Give examples of Eigenvalues and Eigenvectors application in Computer Science

Learning Paradigm
-
Information Processing Theory
-
Domain-specific Learning
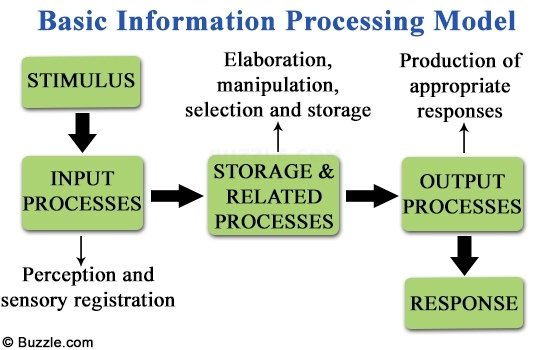
Information Processing Theory
- Meaningful encoding - Information should be meaningful and related to existing knowledge
- Retrieval structure - Cues should also be stored for easy retrieval in the future with connections
- Speedup - Extensive practice improves encoding and retrieval
- Chunking- human brain can only chunk knowledge into the brain with 7 parts, plus or minus two
Domain-specific Learning
- Students learn better when the curriculum is tailored according to the their domain of study
- We should design curriculum based on domain-specific knowledge
- Implement this paradigm by following an algorithmic approach for computer science majors
Learning Activity
Our solution proposal
Will domain-specific learning for Computer Science using a contextual and algorithmic approach help students learn better?
Modules
- Module 1: Introduction to Eigenvalues and Eigenvectors
- Module 2: Properties of Eigenvalues and Eigenvectors
- Module 3: Finding Eigenvalues and Eigenvectors
- Module 4: Eigenvalues and Eigenvectors Theorems
- Module 5: Computing Eigenvalues and Eigenvectors in Python
- Module 6: Application of Eigenvalues and Eigenvectors in Computer Science
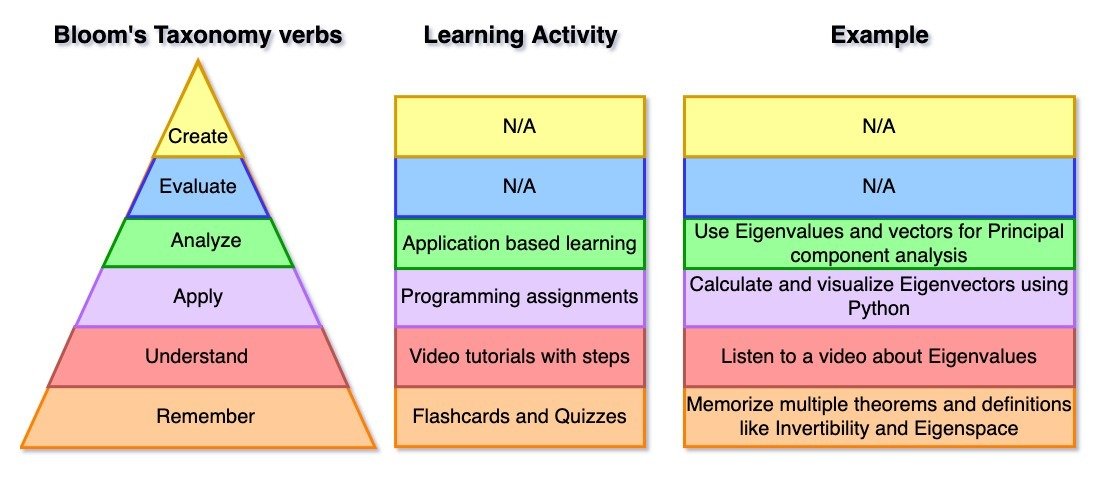
Proposed learning activities
- Step-wise learning with examples
- Flashcards for learning
- Programming challenges
- Quizzes
- Application based learning
Performance Measures
Quantification of learning
Assessment
- Quizzes - calculations, multiple choice questions, fill in the blanks, true and false
- Mini programming challenges - mainly using Python programming language
- Flash card based puzzles - during and after the video lessons
Toolings
Enabling technology for learning
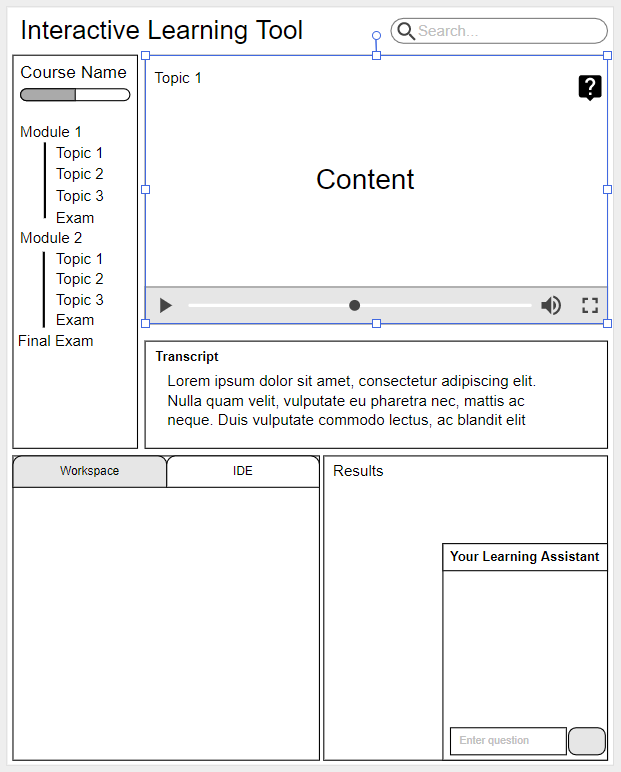
Toolings
- Video player
- Transcripts
- Work-space
- IDE
- Learning Assistant
- Course Explorer

Thank you for your attention!
Bhoomika Agarwal
Debadeep Basu
Ramya Praneetha
Kanya Paramita
Paras Kumar
Reinier Koops
♡2020 by Bhoomika Agarwal. Copying is an act of love. Love is not subject to law. Please copy.
EdTech_Group3
By Bhoomika Agarwal
EdTech_Group3
Conceptual model presentation for Group 3, Educational Technologies
- 340



