Alternative au score de rétention
Score de rétention
Rationnel de base:
- Attendu sans rétention ~ 1/200
- L'observé est-il nettement supérieur à ~1/200 ?
Si N = reads passant sur la jonction TA du MAC + les reads portant l'IES :
A priori: Simple, efficace, pas cher.
Implémentation stat
= Comparaison de proportion: théorique \(p\) VS observée \(p_0\)
$$ H_0 : p = p_0 $$
$$ H_1 : p > p_0 $$ (unilatérale droite)
$$ pvalue = P(p_0 | H_0) $$
Faisable uniquement si:
$$ N \geq 30,\ N\cdotp_0\geq5\ et\ N(1-p_0)\geq5 $$
Très souvent faux pour nous
Option 1 : Approximation loi normale.
Option 2 : Test exact de Fisher
Distribution des p-values
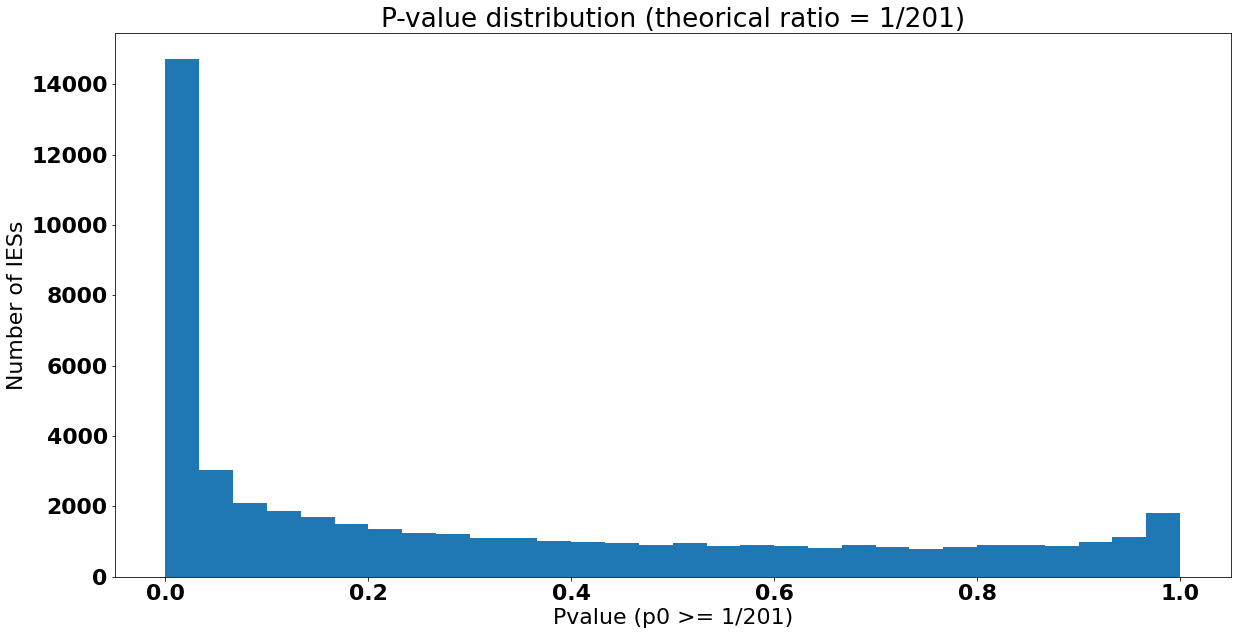
$$ pvalue \leq 5\% \iff Retention \geq 0.00848 $$
Premier non rejet de \(H_0\)
La molécule avec le score de rétention le plus élevé pour laquelle \(H_0\) n'est pas rejetée pour \( \alpha = 5\% \) :
Reads MAC : 70
Reads IES+ : 2
\(p_0= 0.02857... \)
\( Retention = \frac{2}{72} = 0.27..7 \)
> Si on se base hâtivement sur le test, on considérera que ça vient physiquement du MIC
Pourtant...
Reads MAC : 70
Reads IES+ : 2
\(p_0= 0.02857... \)
\( Retention = \frac{2}{72} = 0.27..7 \)
Si la probabilité réelle de rétention de cette IES dans le MAC notée \( P(R|MAC) \) était, par exemple, de 1% :
- Il n'y aurait rien de choquant à n'avoir 0 read IES+ venant du MIC quand on sait que leur probabilité est de ~1/201 du total.
- Il n'y aurait rien de choquant à avoir 2 reads IES+ qui viennent du MAC avec une probabilité de 1/100 par molécule MAC
- Les deux IES+ qu'on aurait piochées ici viendraient très probablement du MAC retenu
- Plus précisément : \( P(MIC|IES^+) = 50\%) \)
- Peut-on considérer que c'est suffisant pour étudier le MIC ? ...
Solution évidente :
> Prendre \( \alpha \) plus grand !
- Quel threshold ?
- Sur quelle base ?
- On va très vite tout éliminer
Soulève d'autres problèmes :

Autre formulation de la situation :
- Si \(pvalue \leq \alpha \) : clairement retenues
- Si \(pvalue > \alpha\), ça peut parfaitement être rempli de séquences retenues quand même.
Or, on veut travailler sur les IES avec \(pvalue > \alpha\)...
Conclusion : Le score de rétention n'est pas une métrique appropriée pour notre problème.
Reformulation
Ce qui nous intéresse est uniquement, pour chaque IES :
- \( P(MIC|IES^+) \) pour chaque IES
- Le score de rétention n'en est qu'un proxy
Idée grossière:
On ne connait pas le pourcentage de molécules MAC qui retiennent l'IES. Mais :
- On connait le nombre d'IES+ obtenu
- On connait le nombre de MIC espéré: \( nb_{MIC} \approx P(MIC) \cdot N \)
- On a donc une idée de l'attendu du nombre de séquences MAC retenant l'IES : \( E( nb_{MACret} ) \approx {nbIES}^+ - E( nbMIC ) \)
De là : On a bien une piste pour estimer la proportion des IES+ qui viennent physiquement du MIC:
Exemple :
- 10.000 reads
-
dont 5000 reads IES+
--> On peut estimer grossièrement \( P(R|MAC) \approx 50\% \)
\( P(MIC |IES⁺) \approx \frac{1}{200} \)
Exemple guide
Exemple guide :
N = 100
\( nb_{IES^+} = 3 \)
\( P(MIC) = \frac{4}{804} \)
P(retention) = ??
\( P(MIC|IES⁺) = ?? \)
Calcul des probabilités :
- On a donc, littéralement, la distribution de probabilité de la variable aléatoire \( \frac{nbMIC}{nbIES+} \) sachant nbIES+.
- \( P(MIC|IES+) \) est approché par la moyenne de cette variable aléatoire.
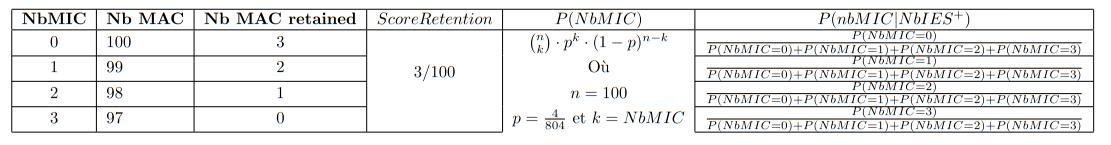
> Pour une IES donnée, on peut donc estimer la probabilité qu'elle vienne du MIC ou du MAC
On peut utiliser cet estimateur en déduire, pour un ensemble de X séquences \(IES^+\), quel sera, en moyenne, la proportion de molécules venant du MIC.
\( \frac{nbMIC}{NbMacRet} \)
0/3
1/3
2/3
3/3
deck
By biocompibens
deck
- 96



