AxioNyx: Simulating Mixed Fuzzy and Cold Dark Matter
Bodo Schwabe, Mateja Gosenca,
Christoph Behrens, Jens C. Niemeyer, Richard Easther
(University of Göttingen & University of Auckland)
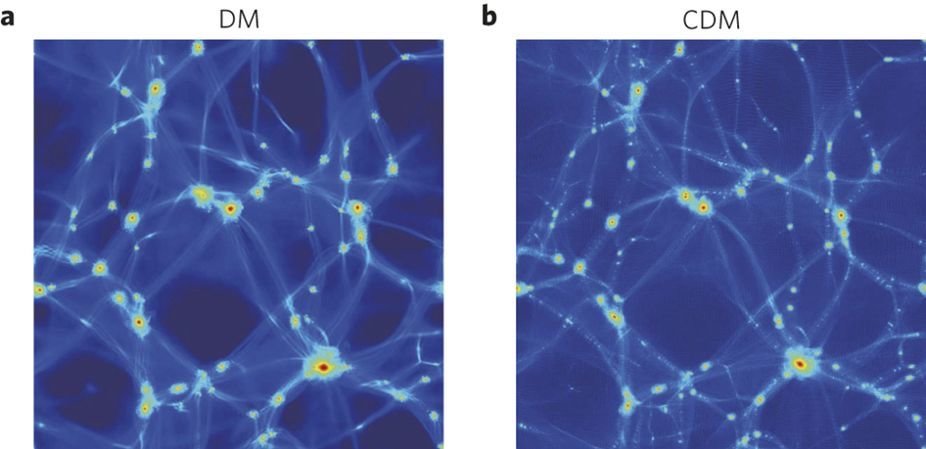
i\hbar\frac{\partial\psi}{\partial t} = -\frac{\hbar^{2}}{2ma^{2}}\nabla^{2}\psi+mV\psi
\nabla^{2}V = \frac{4\pi G}{a}\delta\rho
\delta\rho=|\psi|^{2}
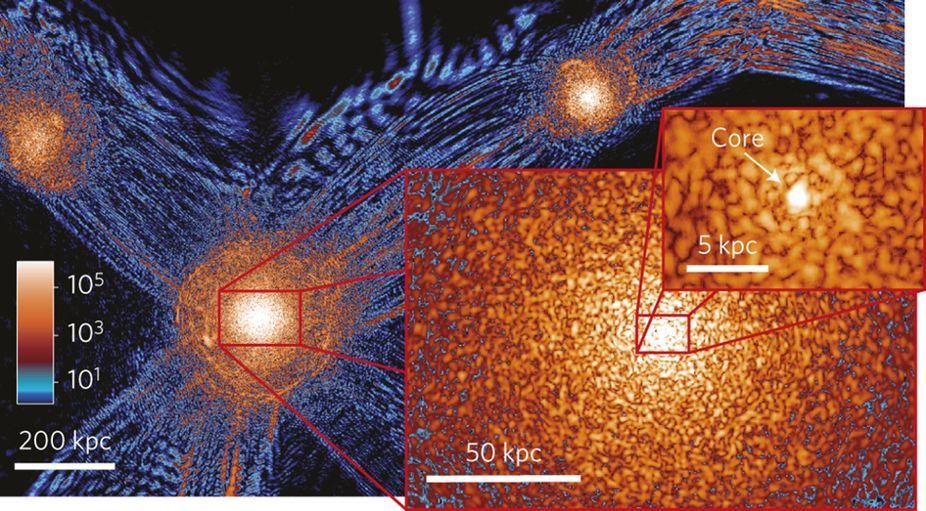
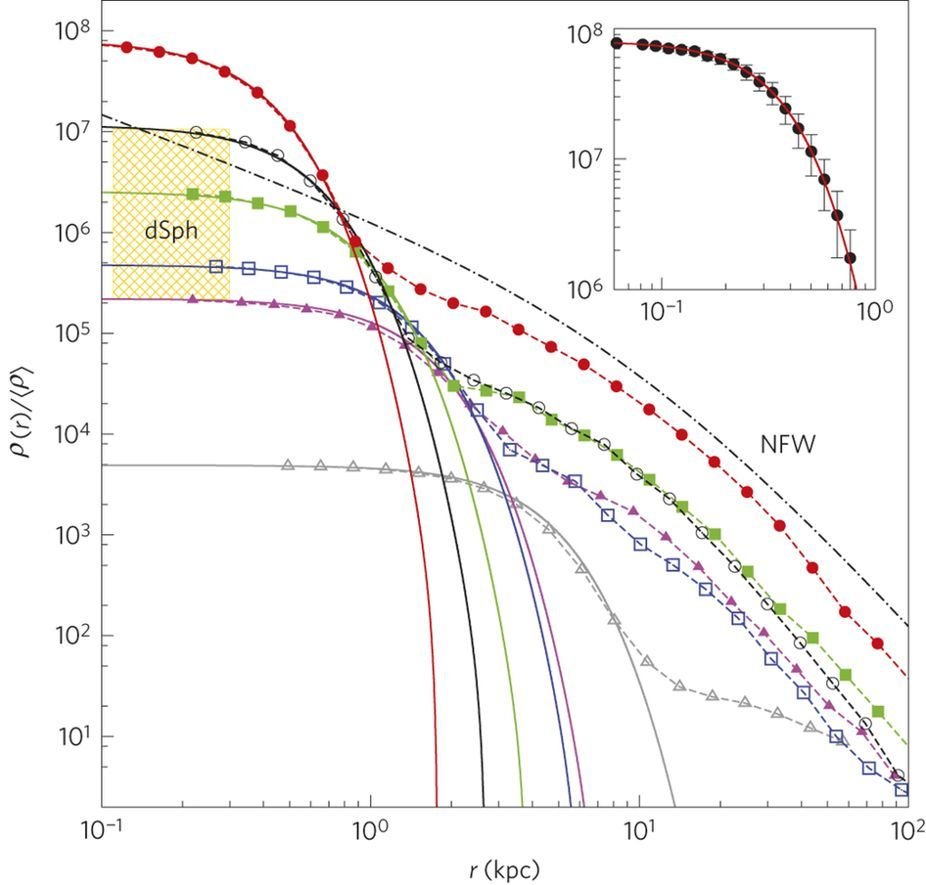
FDM Structure Formation
H.-Y. Schive, T. Chiueh, and T. Broadhurst, Nature Physics, 2014
\lambda_{\rm dB}\sim \hbar/mv_{\rm vir}\sim(\hbar/m)(G\rho)^{-1/2}r^{-1}
\tau_{\rm dB}\sim \hbar/mv^{2}_{\rm vir}
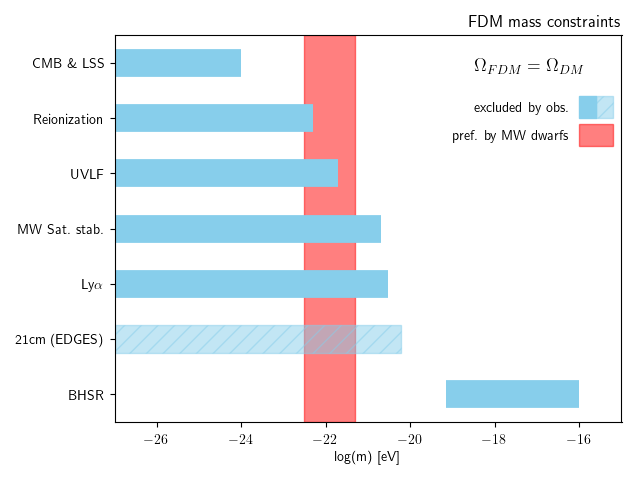
Quantifying Mixed Fuzzy and Cold Dark Matter Halo Dynamics
- Radial density profiles
- CDM velocity dispersion vs. FDM granular structure
- Solitonic core dynamics
using
- AMR grid structure
- Finite differencing
- Spectral codes
- N-body algorithms
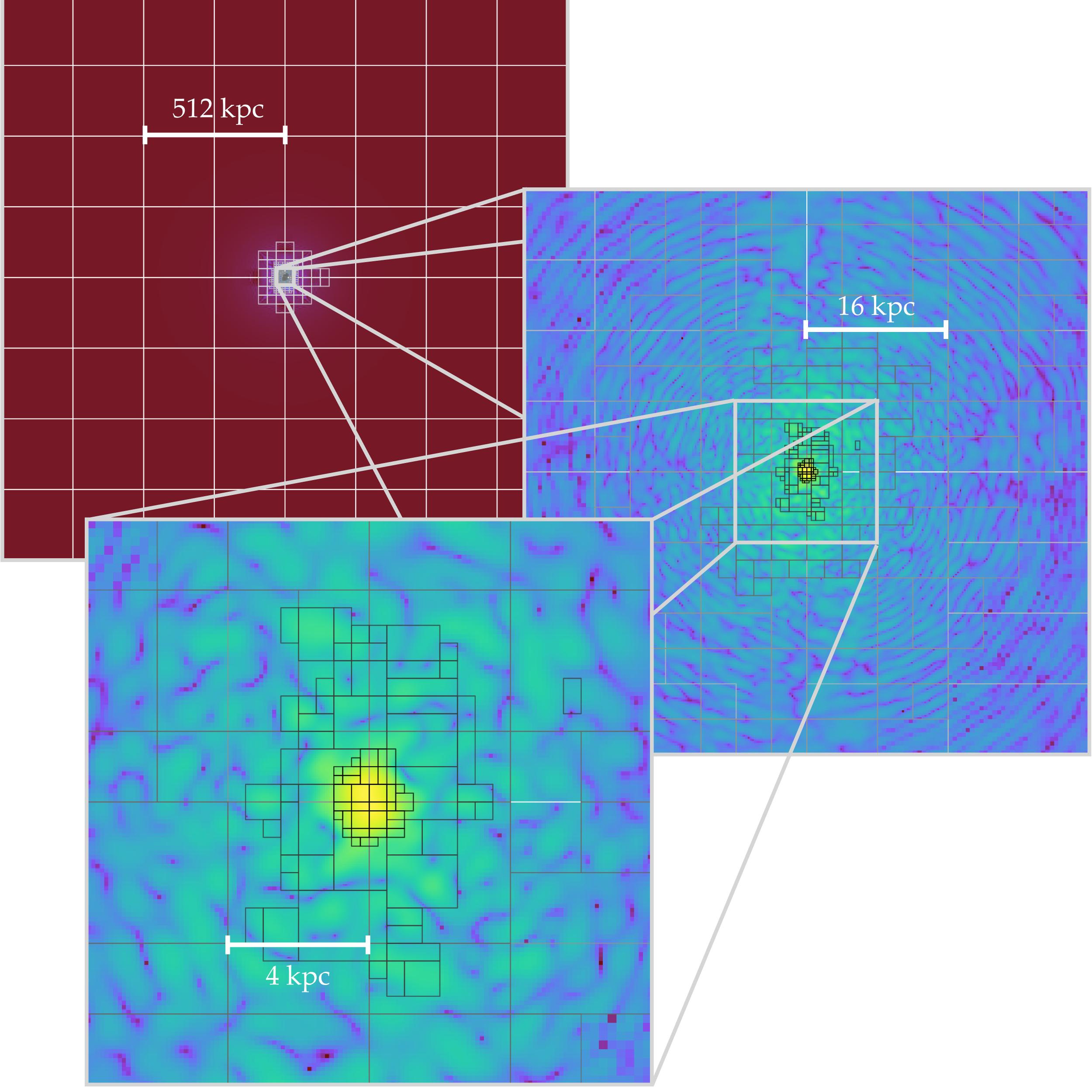
AxioNyx: Simulating Mixed Fuzzy and Cold Dark Matter
Goal:
- AMR simulations for Mixed Dark Matter
- CDM -> N-body scheme
- FDM -> Spectral/Finite-difference method
- Baryonic physics -> Nyx modules for hydrodynamics and feedback
BS, MS, Christoph Behrens, Jens C. Niemeyer, and Richard Easther, arXiv:2007.08256
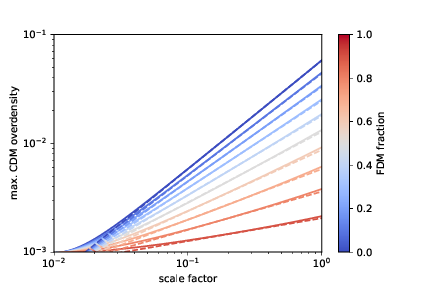
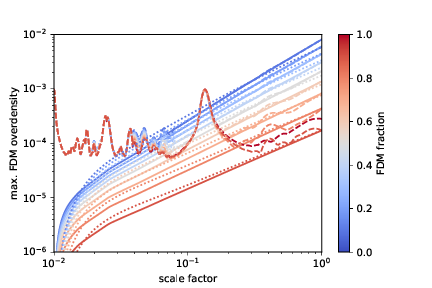
Spherical Collapse - linear
\ddot{\delta}_{\rm FDM}+2H\dot{\delta}_{\rm FDM}+\left(\frac{k^{4}\hbar^{2}}{4m^{2}a^{4}}-4\pi Gf\overline{\rho} \right)\delta_{\rm FDM} = 4\pi G(1-f)\overline{\rho}\delta_{\rm CDM}\\
\ddot{\delta}_{\rm CDM}+2H\dot{\delta}_{\rm CDM}-4\pi G(1-f)\overline{\rho}\delta_{\rm CDM} = 4\pi Gf\overline{\rho}\delta_{\rm FDM}
\delta_{\rm CDM}(a) \propto a^{(\sqrt{1+24(1-f)}-1)/4}
\delta_{\rm FDM}(a) \propto a^{(\sqrt{1+24(1-f)}+3)/4}
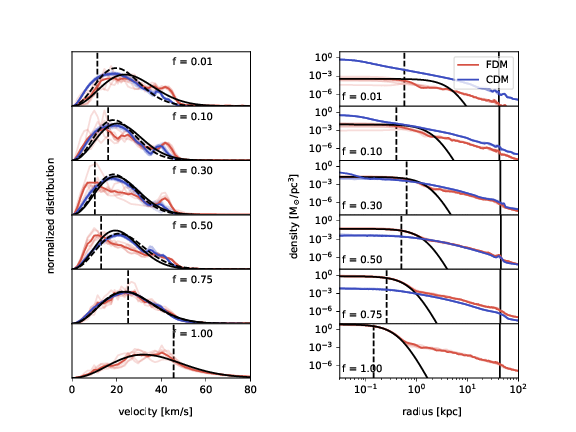
Spherical Collapse - Non-linear
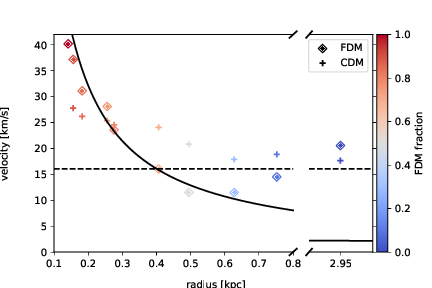
v_c=\frac{2\pi}{7.5}\frac{\hbar}{mr_c}
f(\textbf{v}) = \frac{1}{N}\left|\int\text{d}^3 x\exp\left[-im\textbf{v}\cdot\textbf{x}/\hbar\right]\psi(\text{x})\right|^2
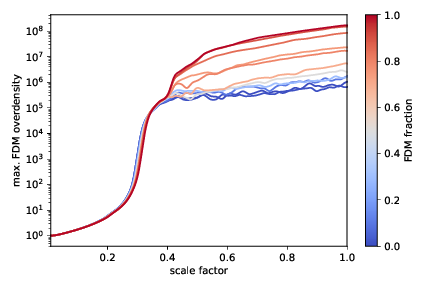
Spherical Collapse - Non-linear
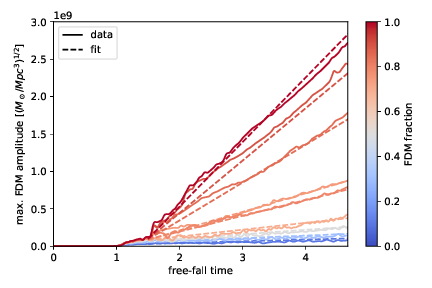
A(t) = A_{1}\cdot (t-t_{0})/\tau_{\text{gr}}+A_{0}f^{1/2}
\tau_{\text{gr}} = \frac{0.7\sqrt{2}}{12\pi^3}\frac{m^3v_c^6}{G^2\rho_{c}^2\Lambda}\simeq 0.015 \frac{t_c}{\Lambda}
Conclusions
-
Distinguishing features of FDM: Strong stochastic density fluctuations in halos on deBroglie length and time scales and formation of stable, oscillating soliton cores in center of halos
- Local FDM density important for experiments but not well constraint yet
- Heavier FDM mass can be best constrained on non-linear, galactic scales (soliton osc., soliton mergers, gravitational heating/cooling, tidal disruption,...)
-- Need further dedicated FDM simulations on galactic scales --
m<10^{-21}\,\text{eV}
- FDM structure formation similar to CDM on super deBroglie scales (except cut-off in initial power spectrum as for WDM)
- Weakly non-linear probes like Lyman-alpha exclude
Fuzzy Dark Matter on Galactic Scales (axionyx)
By bschwabe
