Travelling
Salesman
Problem
Maybe Nemo
Structure
- Problem Statement
- Problem Analysis
- Basic Solutions
- Applications
- Heuristic & Other solutions
- Links & References

Problem Statement
Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?
Model it as a Graph

What's a GRAPH?
representation of a set of objects where some pairs of objects are connected by links
EdgeS
Ordered or Unordered pair of exactly 2 vertices.
Vertices
Fundamental unit of a graph. Think of it as a point. Can be disconnected.

GRAPH
Ordered Pair G =(V, E)
V = Set of vertices
E = Set of edges
Directed
Edges are two way
Edge(a,b) != Edge(b,a)
Undirected
Edges have no orientation.
Edge(a,b) = Edge(b,a)


Asymmetric
In the asymmetric TSP, paths may not exist in both directions or the distances might be different, forming a directed graph.
One-way streets, for eg.
symmetric
The distance between two cities is the same in each opposite direction, forming an undirected graph.
This symmetry halves the number of possible solutions.
Most common type of TSP.
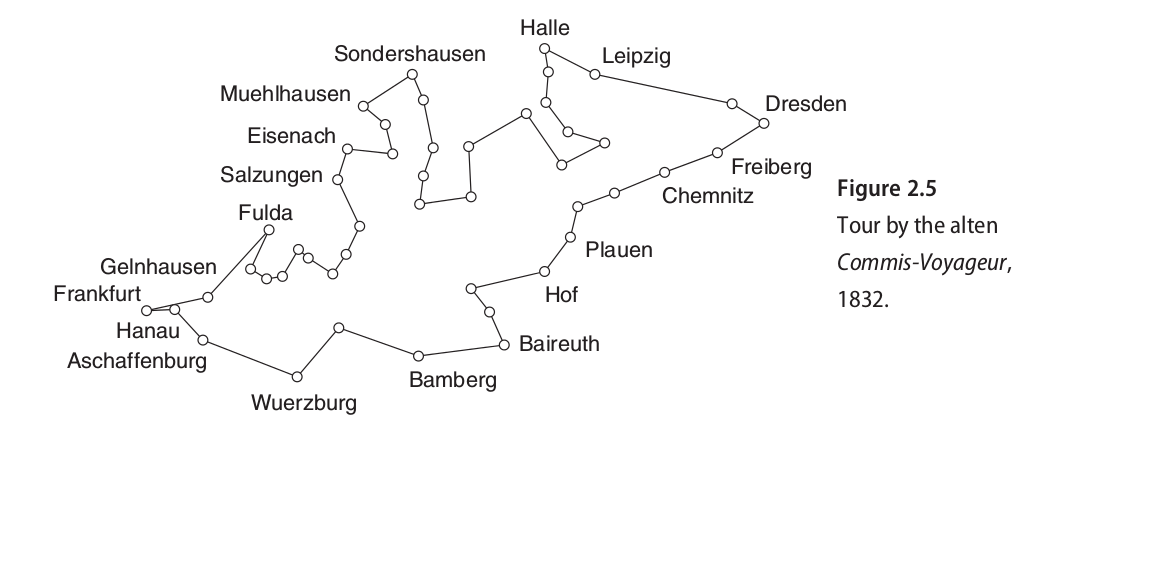
Problem Statement
undirected weighted graph
city = graph's vertices
path = graph's edges
distance = edge's length
Minimize total distance after visiting all vertices.
Often, graph is complete as well
Solve*
TSP
=
GET
$1,000,000
Problem Complexity
ComplexiTY

| Year | Vertices |
|---|---|
| 1954 | 49 Cities (USA) |
| 1971 | 64 Points |
| 1975 | 80 Points |
| 1977 | 120 Cities (Germany) |
| 1987 | 318 Points |
| 1987 | 532, 666, 1002, 2392 |
| 1992 | 3038 Points |
TSP Records
1998 - 13,509 Cities
in USA
SWEDEN (2004)
24978 Cities

85,900
Points
Computer Chip Production
(2006)

Applications
Navigation

Mapping GEnomes


Printed Circuit Boards
Other Fields
- Data Mining
- Slewing
- X-ray Crystallography
- Engravings, Etchings
- Custom Chip Mfg.
- Cutting patterns
- Compression
Solutions
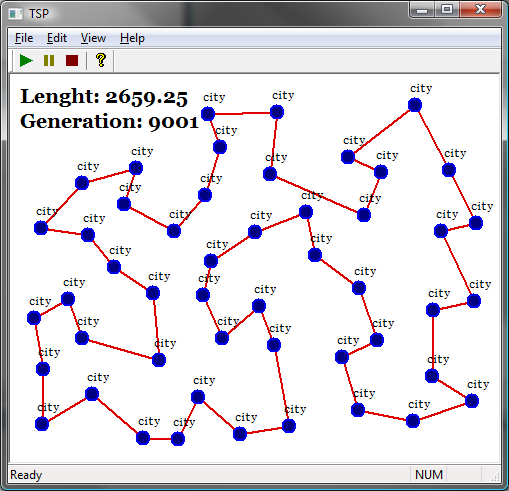
Brute Force Search

Nearest Neighbour
Greedy Algorithm
Partial Tour
Method
Ant Colony Optimization

- Travel to all cities
- Choose closer cities (visibility)
- Probability of choosing ∝ pheromone
- Deposit pheromone on path travelled
- Iterate

References
- By David Stanley from Nanaimo, Canada (Balloon Salesman Uploaded by russavia) [CC-BY-2.0], via Wikimedia Commons
- TSP Cartoon, Courtesy Randal Munroe (xkcd.com)
- In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation, William J Cook
William J COOK
In Pursuit
of the
Travelling
Salesman

Thank You
TRAVELLING
SALESMAN
MOVIE
.COM

Travelling Salesman Problem
By Nemo
Travelling Salesman Problem
A short talk on the Travelling Salesman Problem.
- 3,398



