Cosmological Surveys in a nutshell
Learning summary statistics with machine learning
Carolina Cuesta-Lazaro
16th December 2021 - Oxford

Collaborators: Cheng-Zong Ruan, Yosuke Kobayashi, Alexander Eggemeier, Pauline Zarrouk, Sownak Bose, Takahiro Nishimichi, Baojiu Li, Carlton Baugh
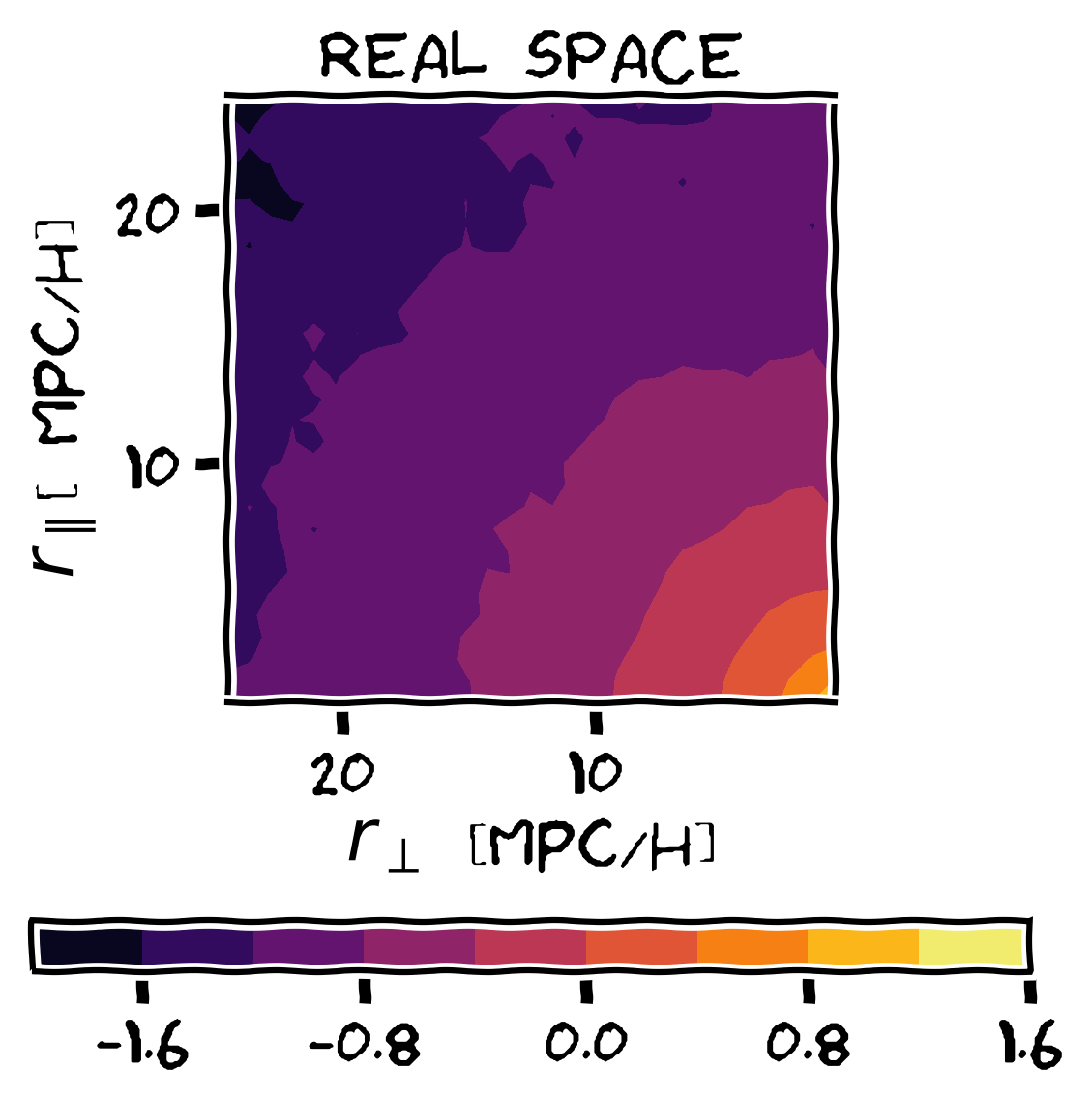

1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \blue{\xi^R(r)}\right) \red{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
\blue{\xi^R(r)}
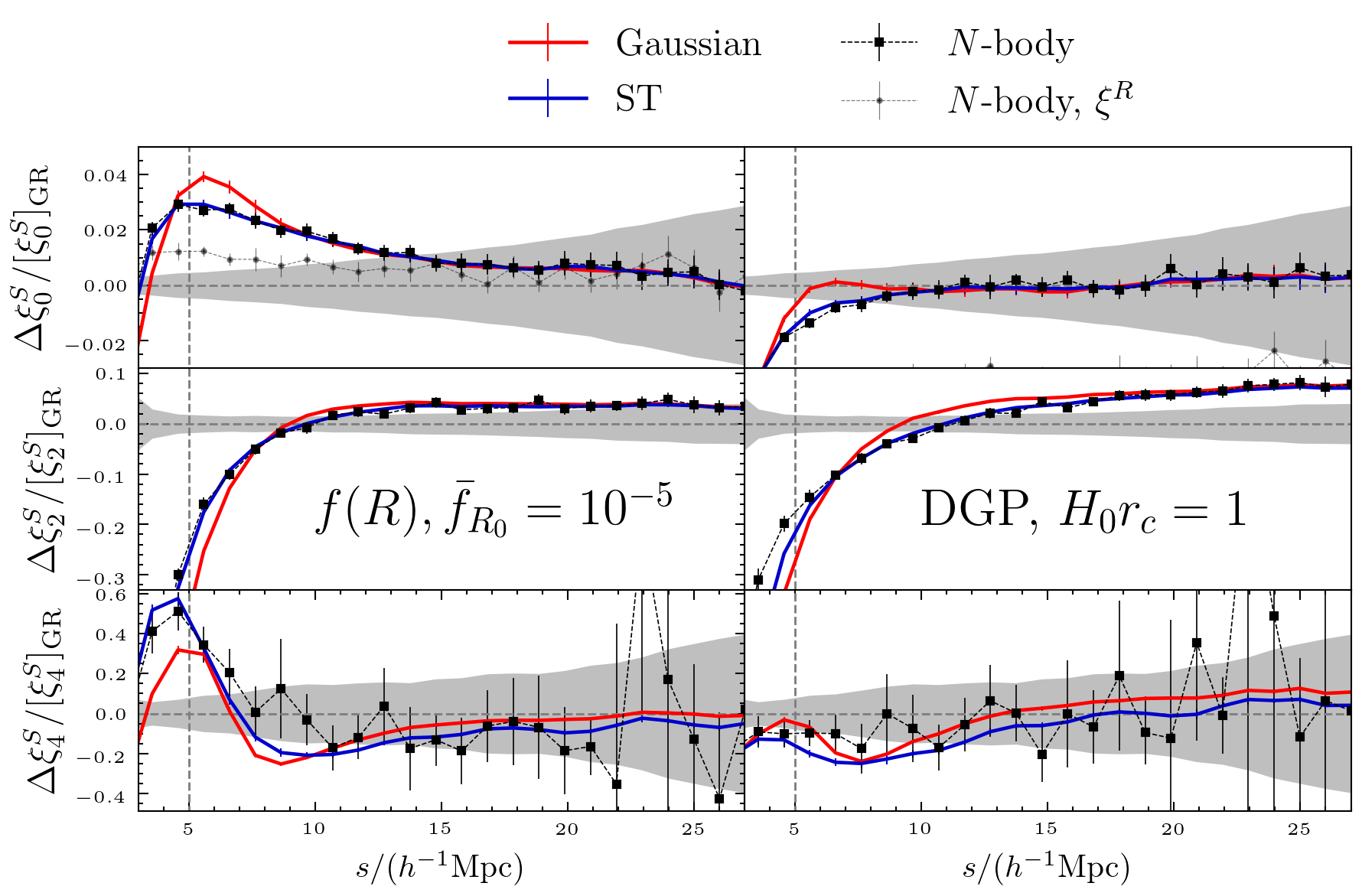
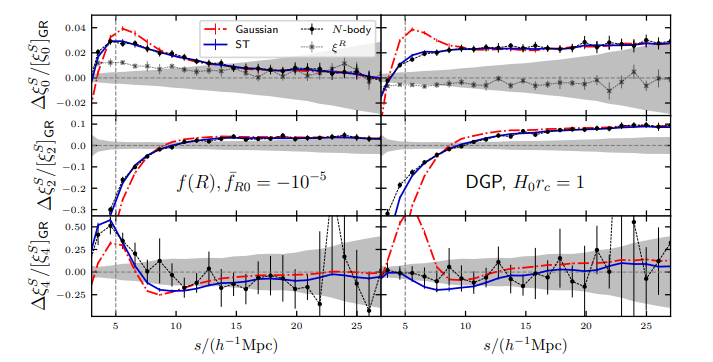
Two representative MG models:
- The background expansion is the same as LCDM
- One parameter to describe deviations from LCDM
(same large scale real space clustering)
Cosmology =
\{\vec{c}\}
\vec{c}_i

Neural Network Emulator
\vec{c}, \mathrm{redshift}, M_h
\xi^R_{hh}(r|M_h)
v_{hh}(r|M_h)
\xi^R_{hh}(r|c_i, M_h)
v_{hh}(r|c_i, M_h)
Galaxy =
\{\vec{g}\}
\xi_{gg} \propto \int d M_h W(\vec{g}_j, M_h) \xi_{hh}(M_h)
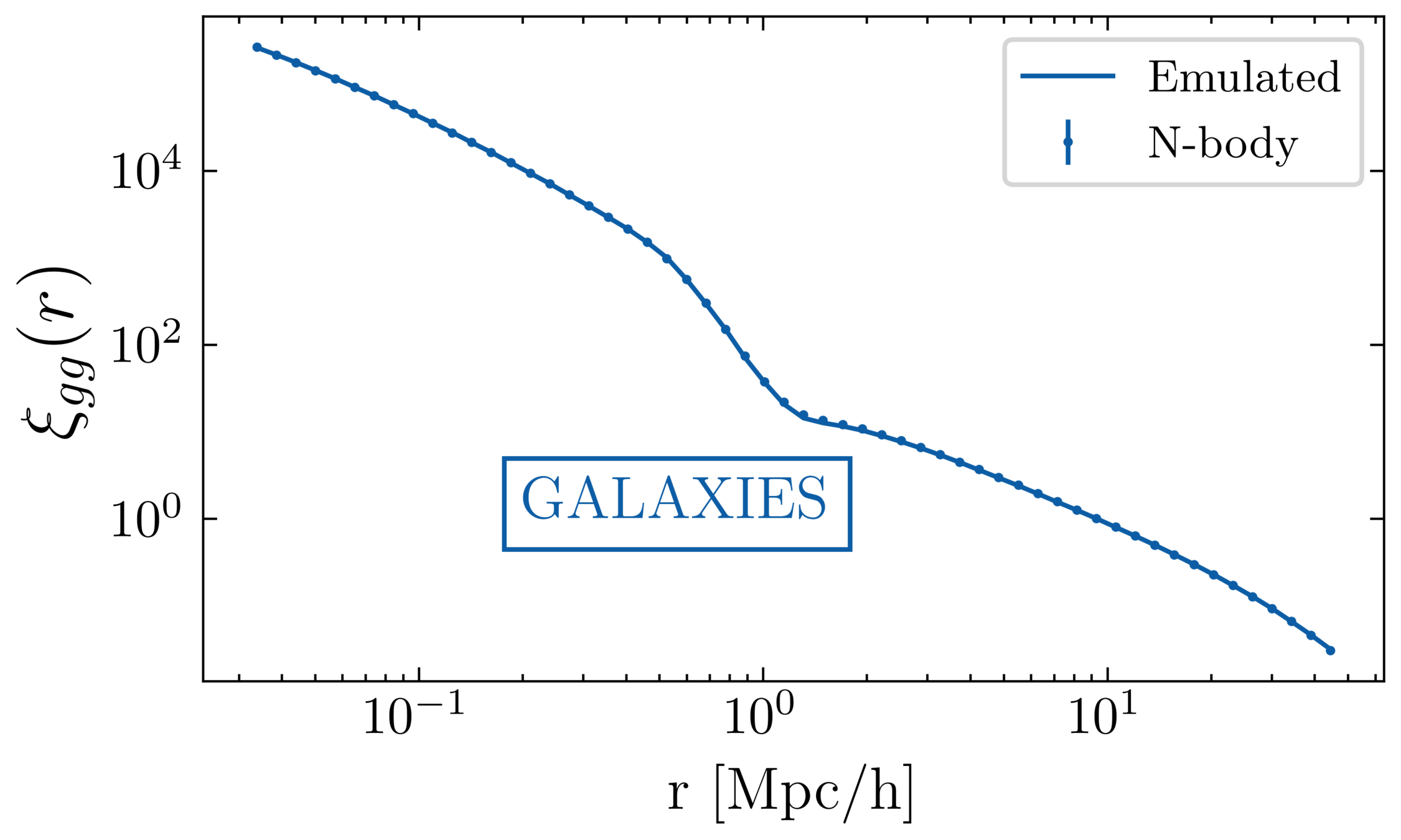
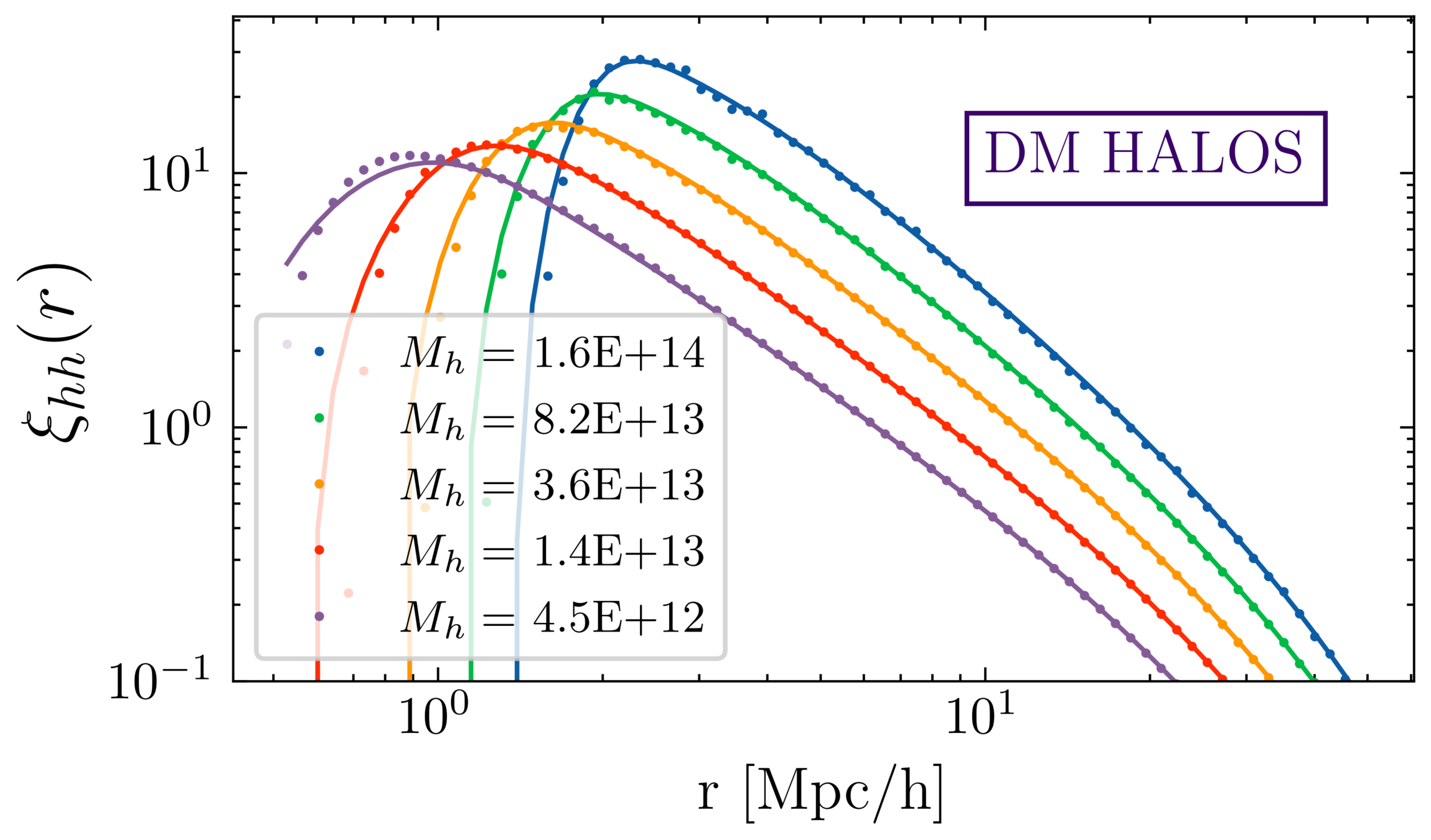
\xi_{gg} \propto \int d M_h W(\vec{g}_j, M_h) \xi_{hh}(M_h)
Voids
Clusters
r [h^{-1} \mathrm{Mpc}]
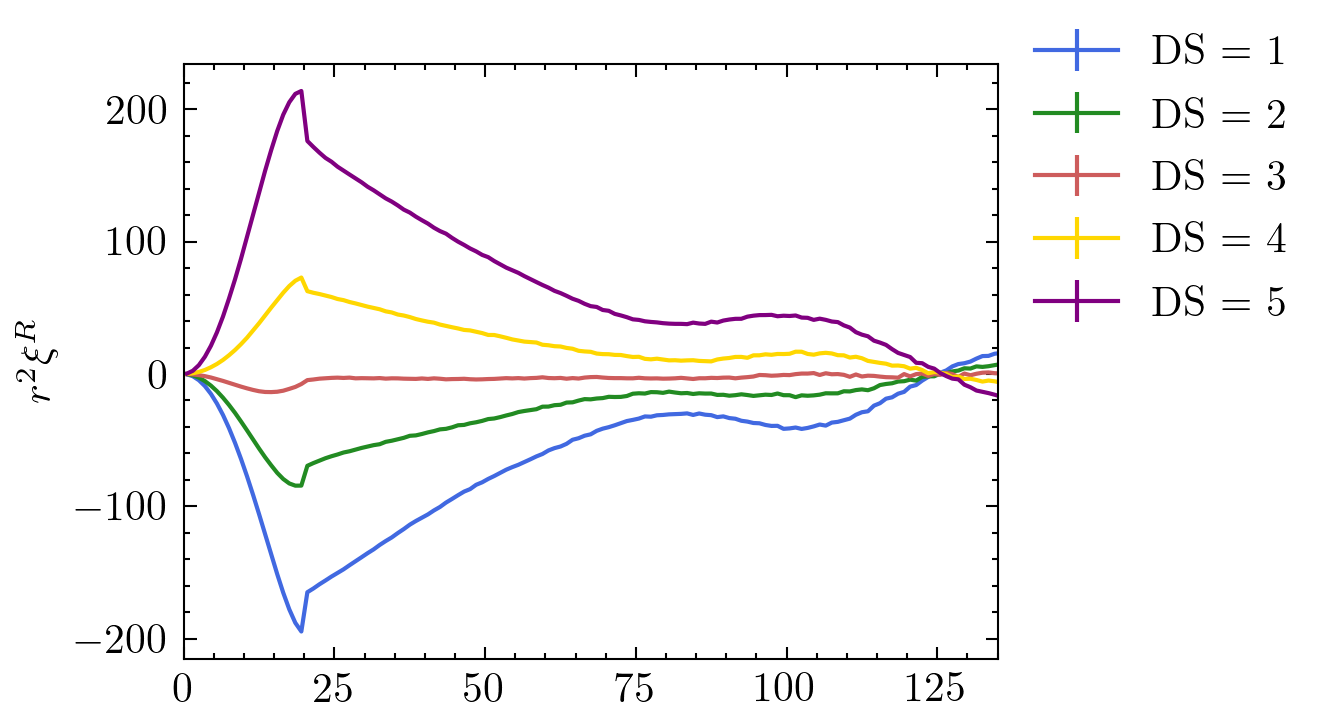
\Omega_M
\Omega_\Lambda
\sigma_8
Inputs
x
Neural network
f
Representation
(Summary statistic)
r = f(x)
Output
o = g(r)
Oxford
By carol cuesta
Oxford
- 487



