Redshift surveys in a nutshell
Learning summary statistics with ML
Carolina Cuesta-Lazaro
19th January 2022 - Waterloo Astronomy Seminar
Collaborators: Cheng-Zong Ruan, Yosuke Kobayashi, Alexander Eggemeier, Pauline Zarrouk, Sownak Bose, Takahiro Nishimichi, Baojiu Li, Carlton Baugh
The golden days of Cosmology:
A five parameter Universe
\Omega_m
\Omega_b
\Omega_\Lambda
A_s
n_s
Initial Conditions
Dynamics
Dark energy
Dark matter
Ordinary matter
Amplitude initial density field
Scale dependence
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}}
t = 380,000 \: \mathrm{years}
\xi(r) = <\delta(x) \delta(x+r)>
\delta = \red{F}(\delta_i)
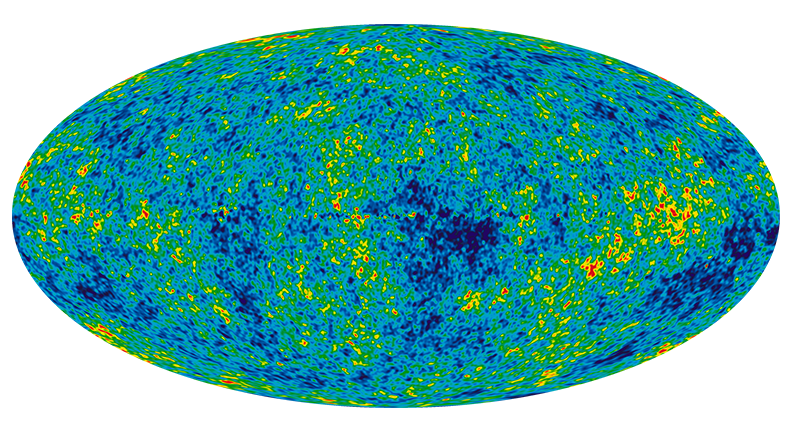
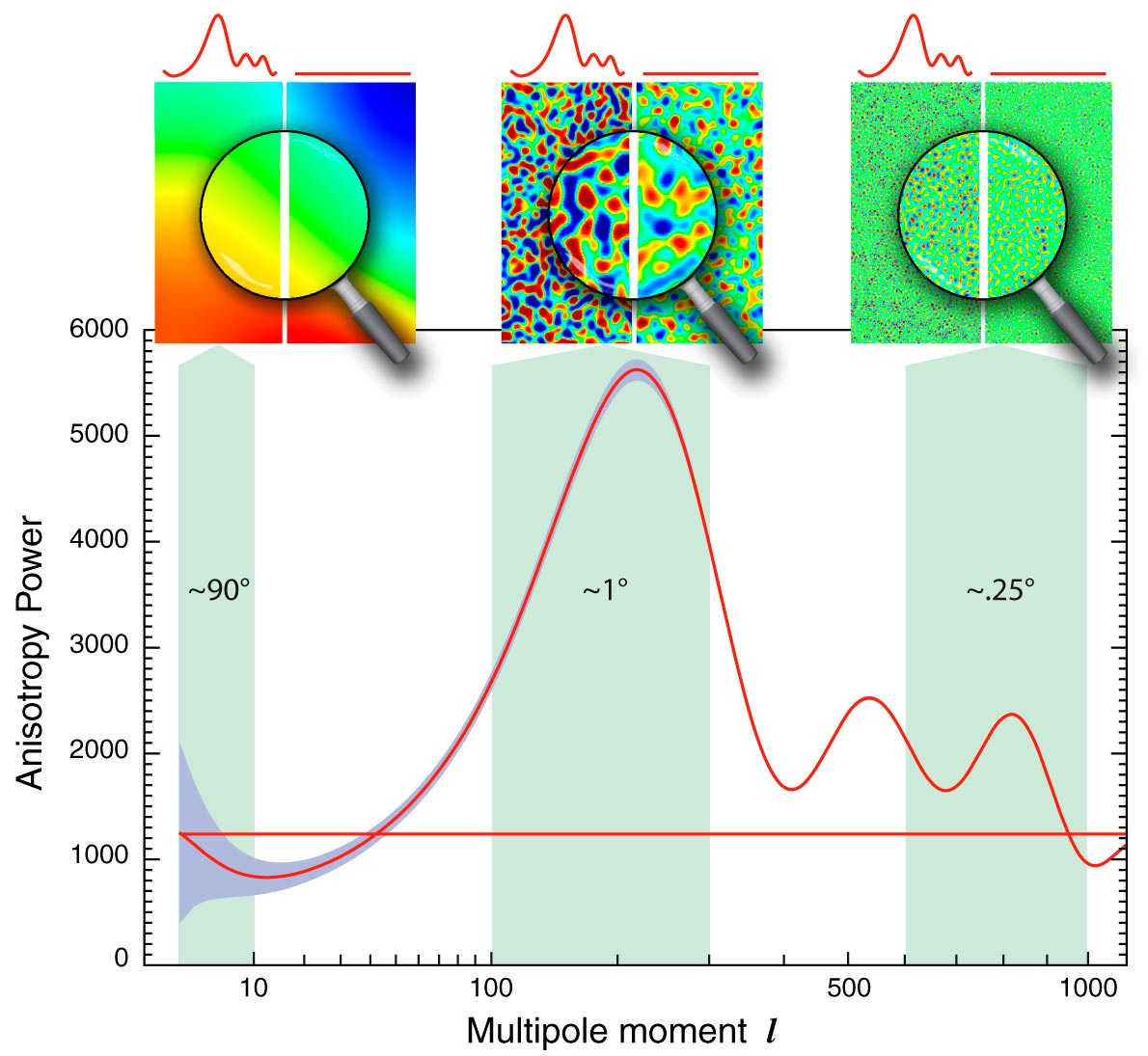
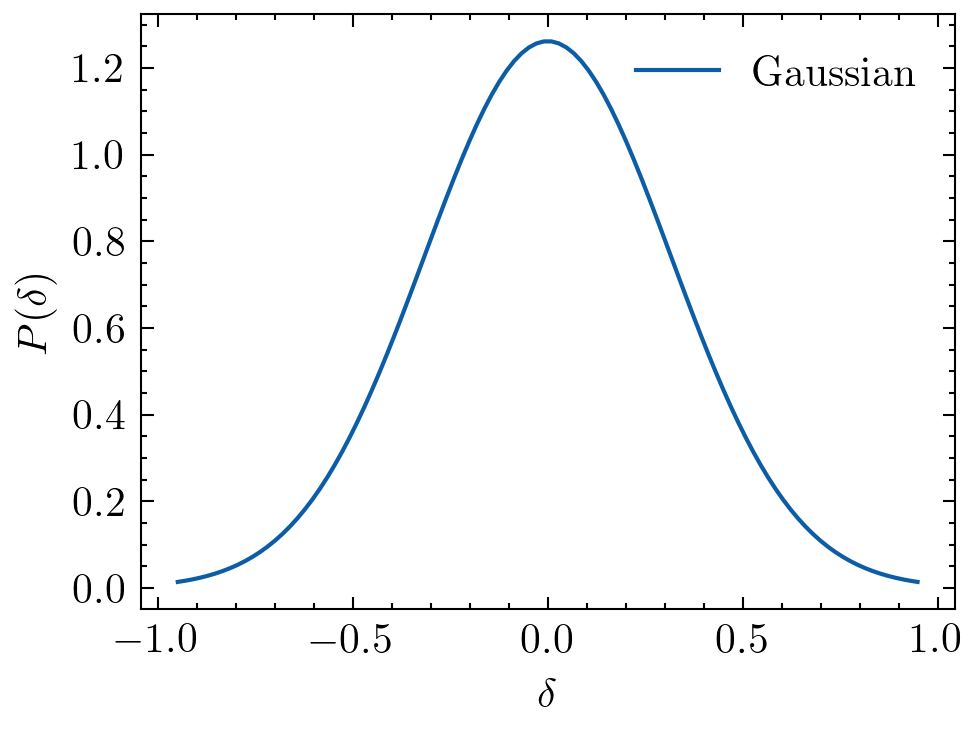
Linear
Credit: NASA / WMAP SCIENCE TEAM
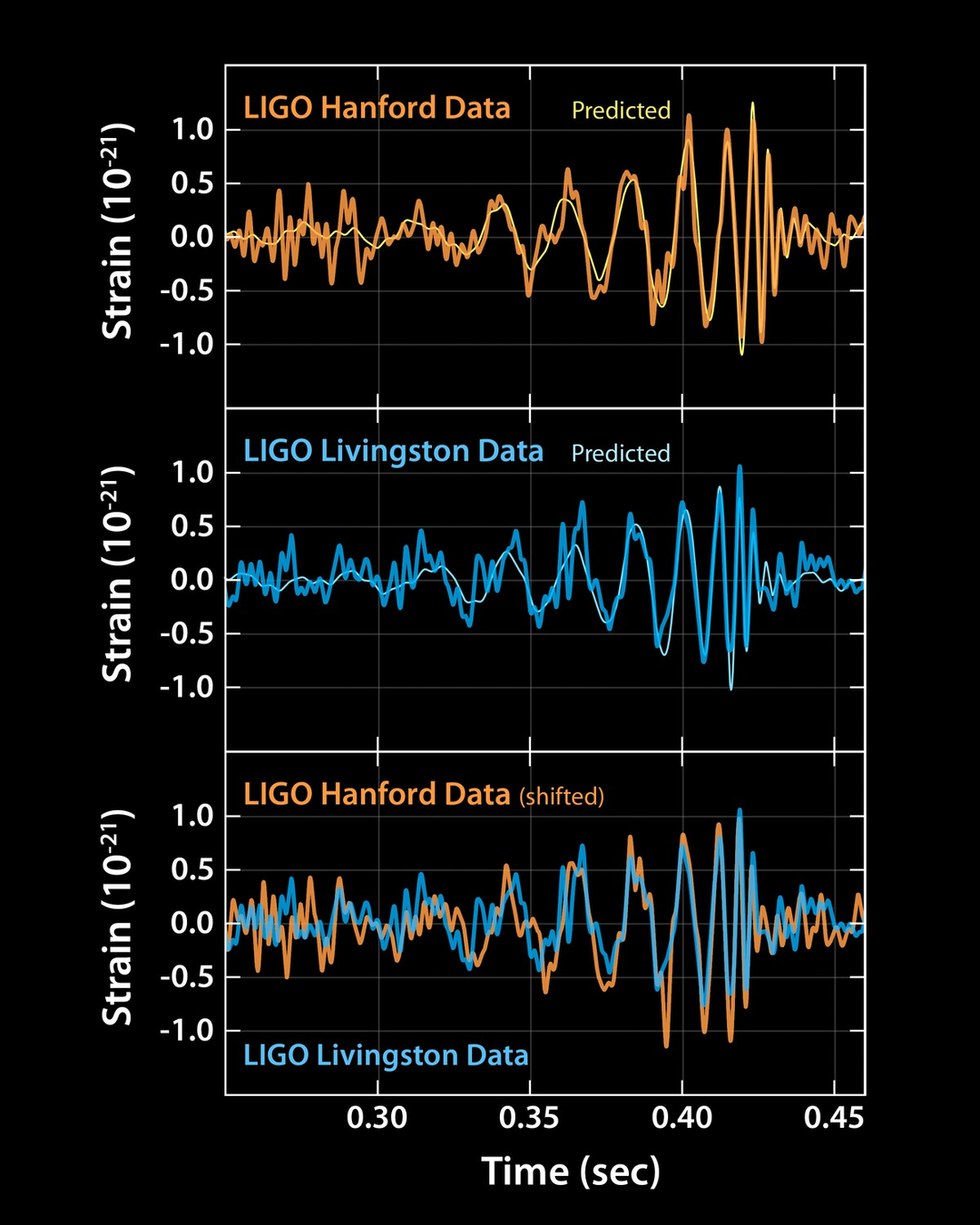
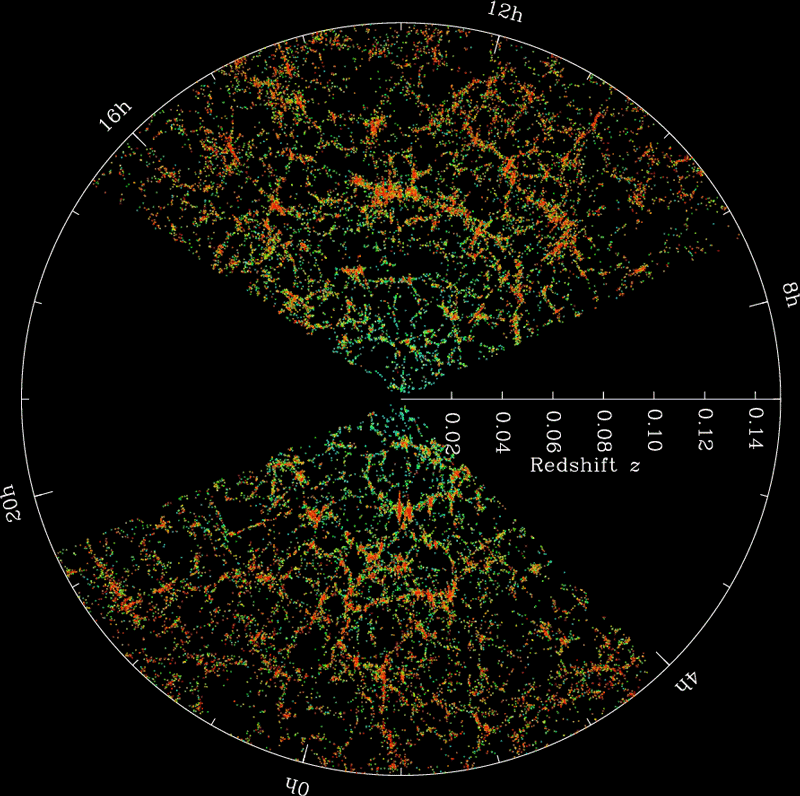
GALAXY CLUSTERING
GRAVITATIONAL WAVES
GRAVITATIONAL LENSING
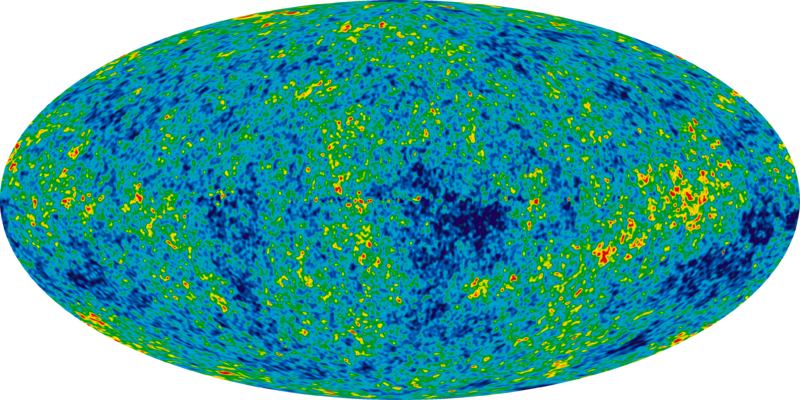
Early Universe
~linear
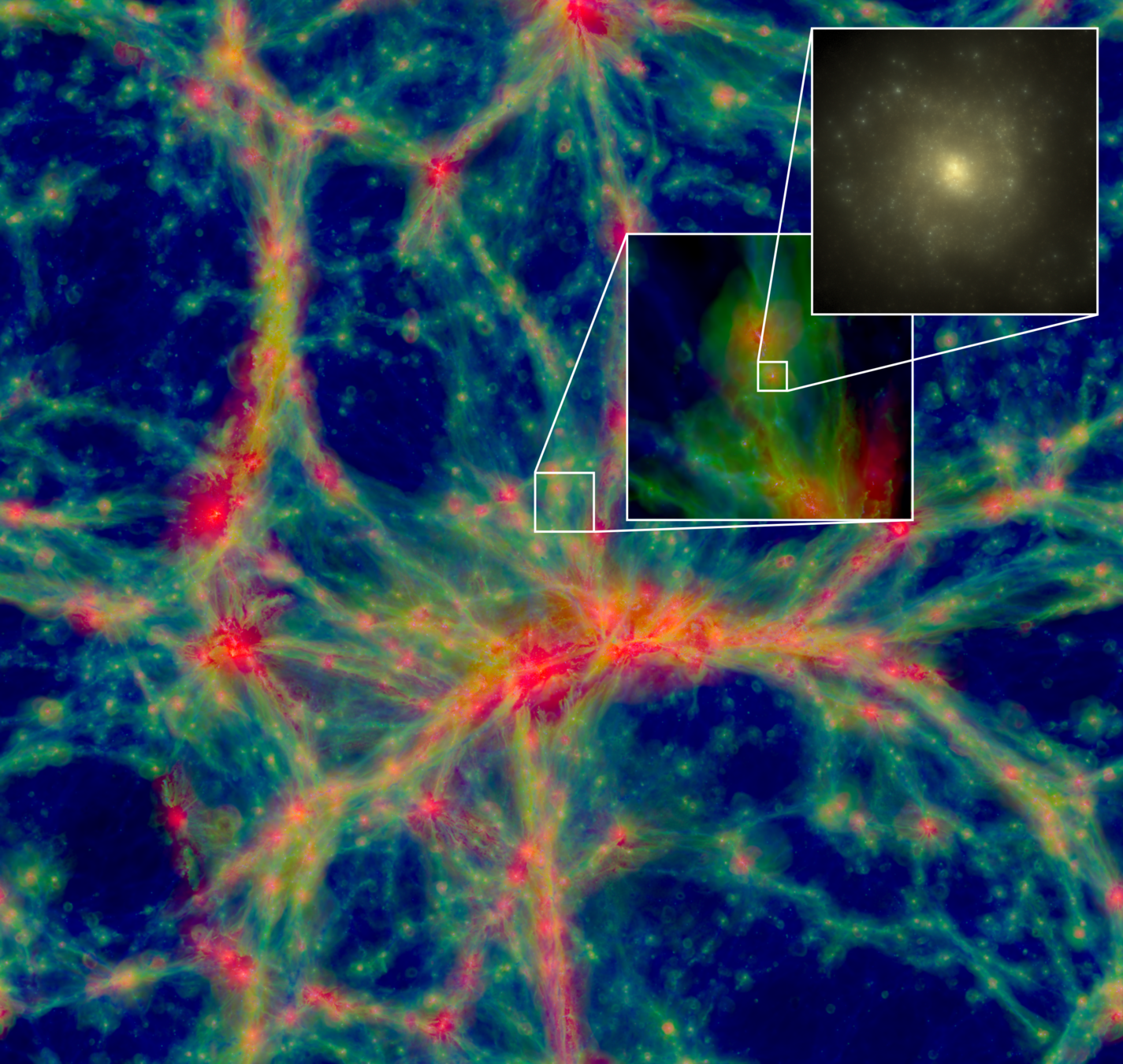
Gravity
Late Universe
Non-linear
Credit: S. Codis+16
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}} << 1
\delta >> 1
Non-linearity = PT predictions inaccurate
Credit: S. Codis+16
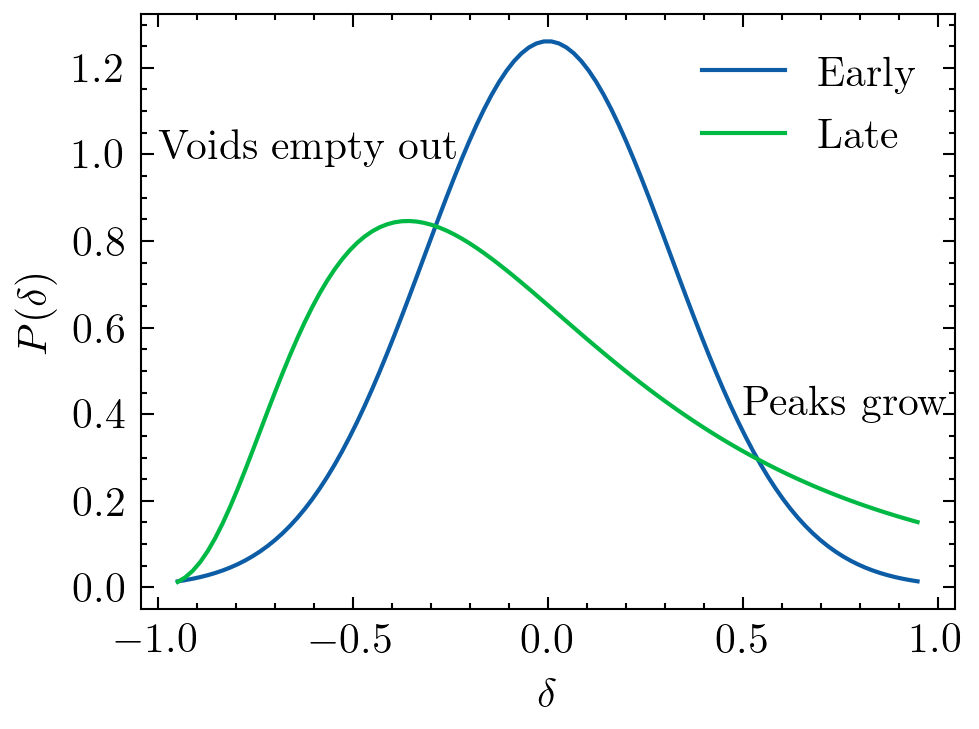
Early Universe
~linear
Gravity
Late Universe
Non-linear
Credit: S. Codis+16
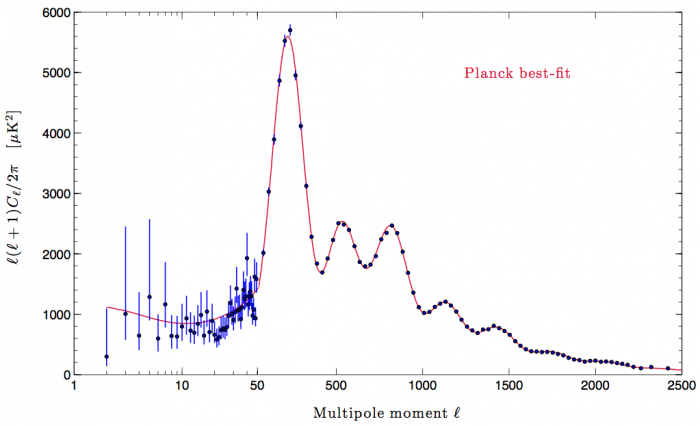
Non-Guassianity
Second moment not optimal
\delta = \frac{\rho - \bar{\rho}}{\bar{\rho}} << 1
\delta >> 1
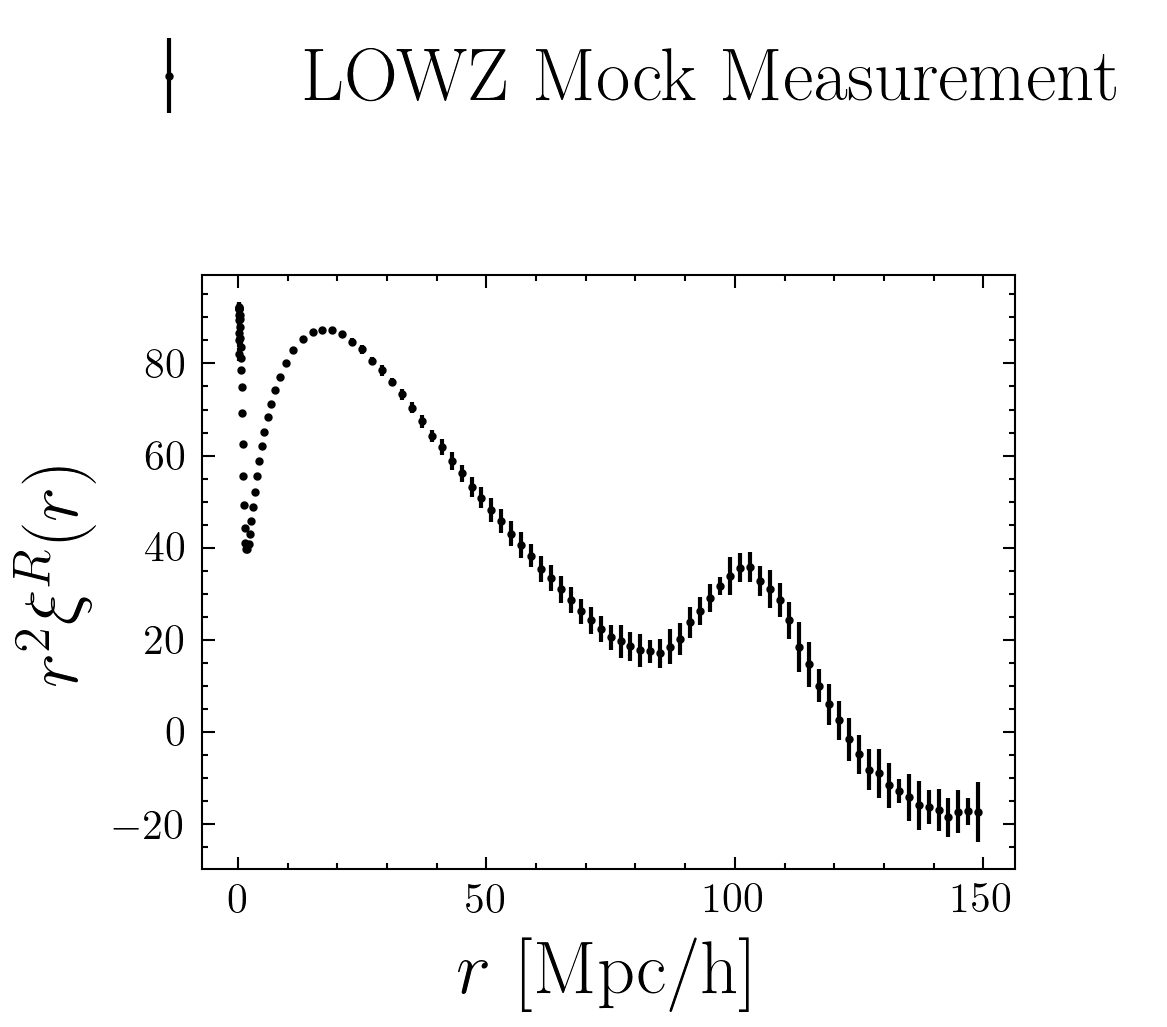
Machine Learning as a solution to
- Non-linearities Produce accurate predictions based on N-body simulations
- Non-Gaussianity Extract cosmological information at the field level
(\vec{\theta}_i, z_i)
z_i = z_{\mathrm{Cosmological} }
+ z_{\mathrm{Doppler}}
\chi(z) = \int_0^z \frac{dz'}{H(z')}
+ \frac{v_{\mathrm{pec}}}{aH(a)}
\chi_i
Space-time
geometetry
Energy content
Adding new degrees of freedom
- To the energy content (dynamic) DARK ENERGY
- To the way space-time geometry reacts to the energy content MODIFIED GRAVITY (FIFTH FORCES)
?
Fifth forces modify structure growth
GROWTH
- GRAVITY
- FIFTH FORCE
+ EXPANSION
Credit: Cartoon depicting Willem de Sitter as Lambda from Algemeen Handelsblad (1930).
Cosmology =
\{\vec{c}\}
Main Assumptions
- Galaxies don't impact dark matter clustering
- Number of galaxies depends on halo mass only
- We don't know the Initial Conditions
- Data is very high dimensional
- Large number of parameters to constrain
- N-body sims extremely slow to run! (Sampling parameter space > O(10^6) calls)
Cosmology =
Galaxy =
\{\vec{c}\}
\{\vec{g}\}
\Omega_M
P(\vec{c}|\vec{D})
?
Summarise the data
\mathcal{O}(100)
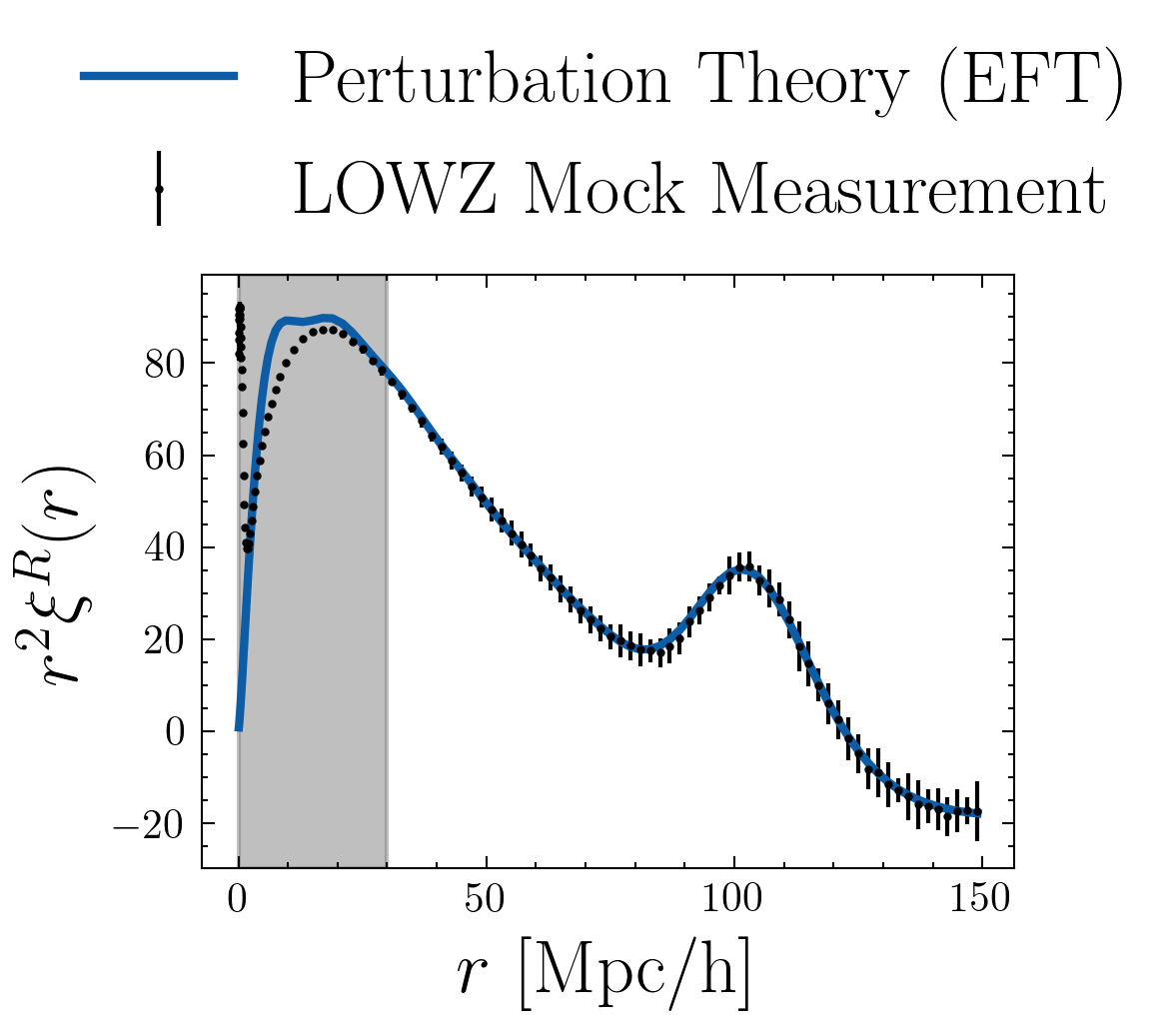
N-body simulations
\xi_{gg} = f(\vec{c}, \vec{g}, z)
How to emulate?
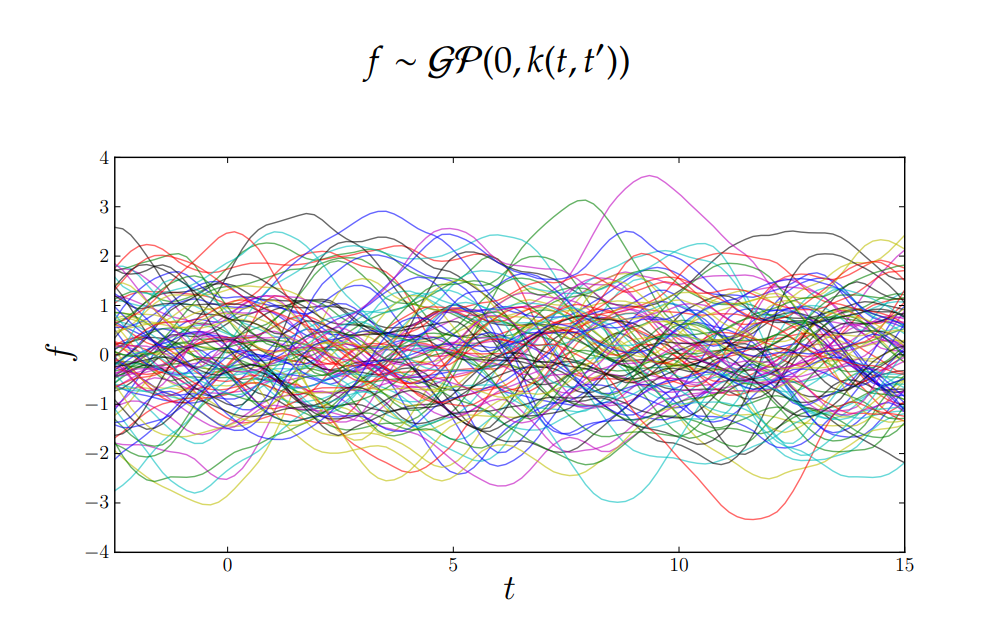
Credit: James Hensman
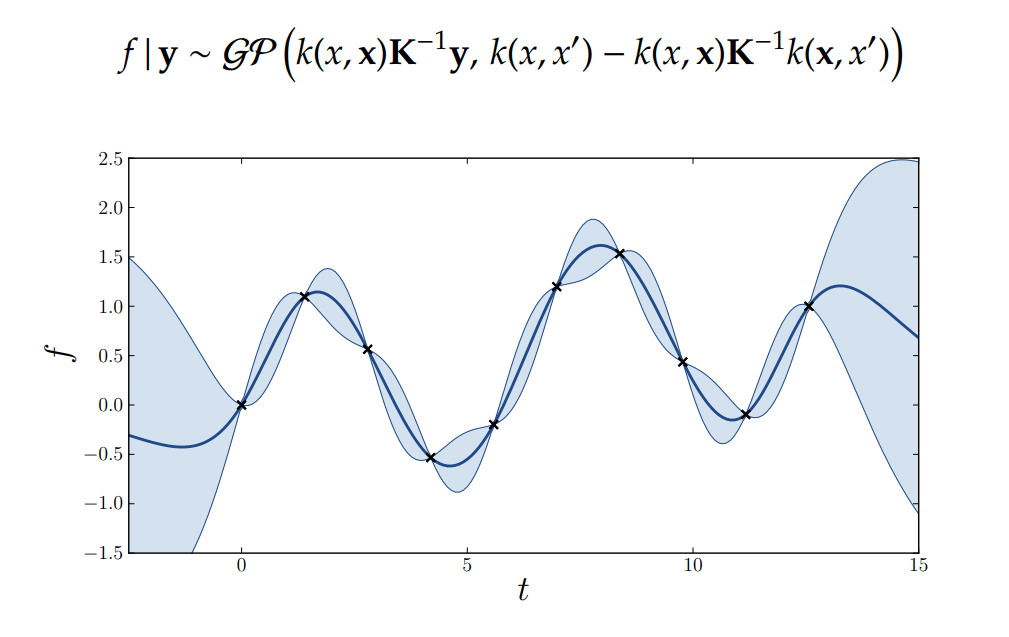
Credit: James Hensman
Optimize the marginal likelihood: Analytical solution!
Pros
- Easy to get going
- Small number of free parameters
Cons
- Scales badly with training set size O(n^3)
- Scales badly with number of input features
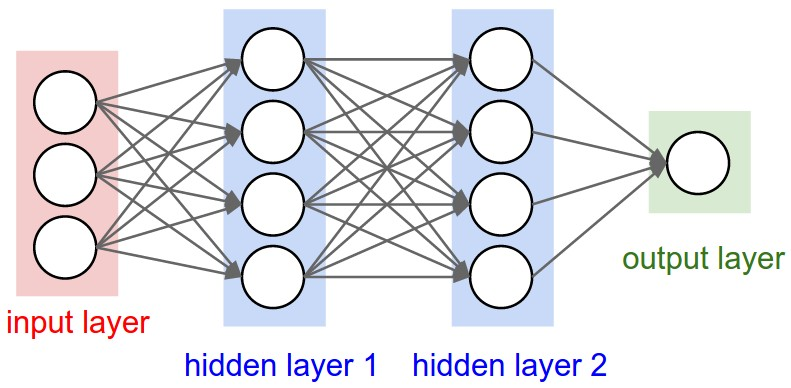
Credit: https://cs231n.github.io/convolutional-networks/
\hat{\xi}(r)
\mathcal{L} = \frac{1}{n} \sum |\hat{\xi}(r) - \xi(r)|
\Omega_m
r
\Omega_\Lambda
...
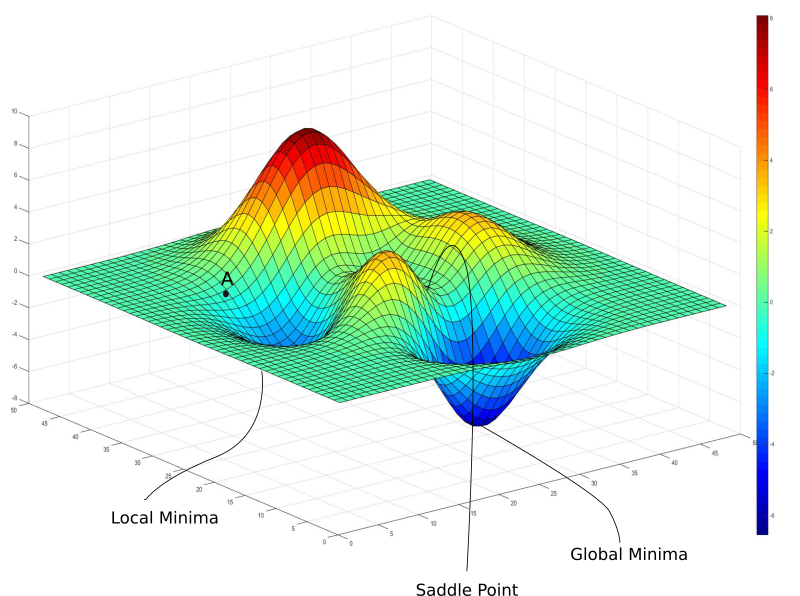
Loss Value
Weights
Weights
+
+
+
+
Network A
Network B
Pros
- Fast, does not scale with n
- Can model large input features
Cons
- Prone to overfitting: But ways to avoid it
- "Harder" to train (requires more exploration)
What to emulate?
- Flexibility: Vary galaxy tracers, and their cross-correlations. Marginalising over g requires flexible g!
-
1% accuracy1-sigma accuracy:- Emulator only as good as data used for training
- Simplify input/output relation through physical models
\xi_{hh}^S = \red{F}(\blue{\xi_{hh}^R(r|\vec{c})}, \blue{v^{i}_{hh}(r|\vec{c})})
\xi_{gg}^S(\vec{s}|\vec{c},\vec{g},z) = \red{\mathcal{G}}(\blue{\xi_{hh}^S}(\vec{s}|\vec{c},z), \vec{g})
Neural Net
Analytical
1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \blue{\xi^R(r)}\right) \red{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
\blue{\xi^R(r)}
\xi^S(s_\perp, s_\parallel)
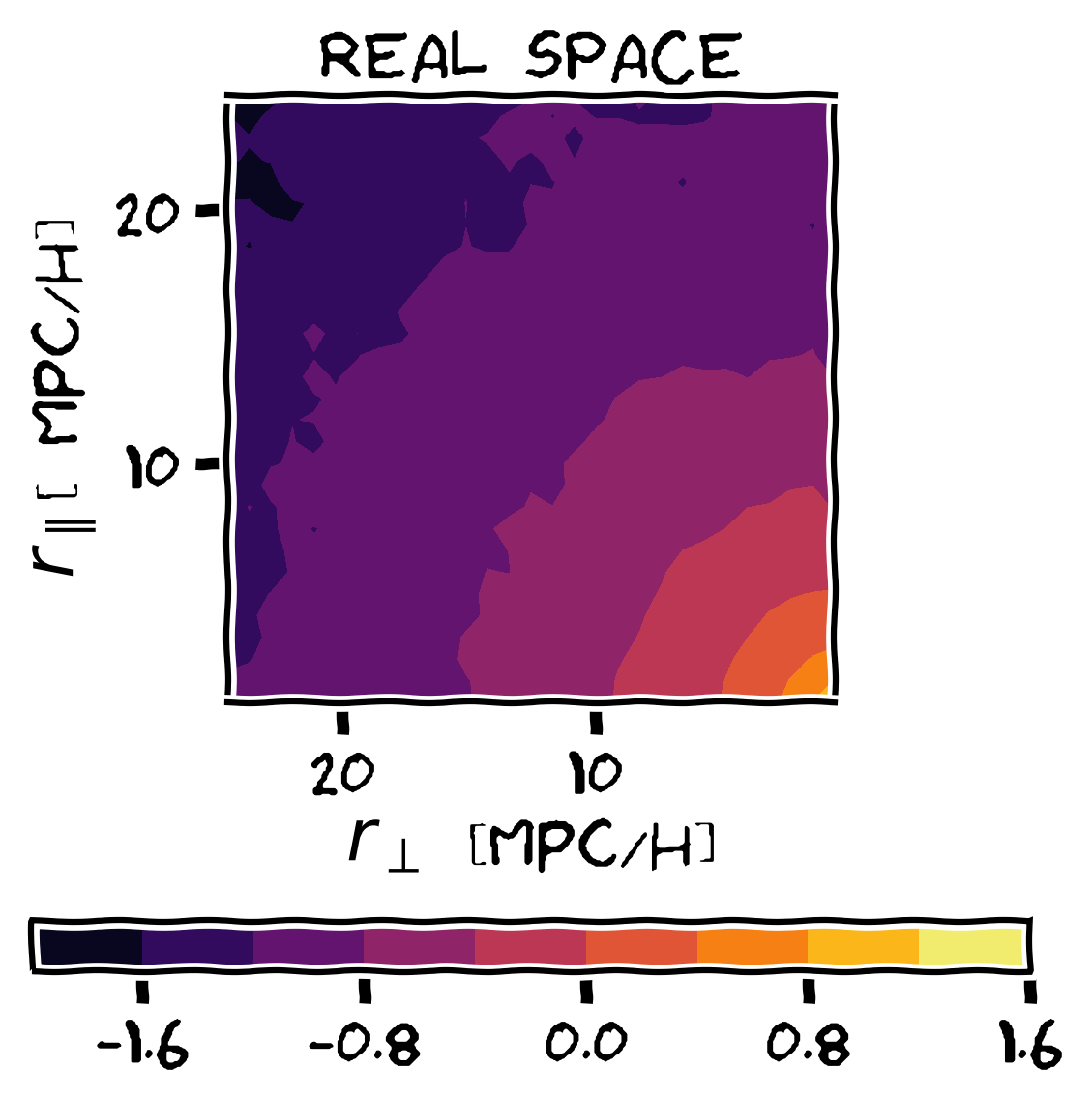
The Streaming Model
1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \xi^R(r)\right) \red{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
PAIRWISE VELOCITY
DISTRIBUTION
r
v_{\parallel,1}
v_{\parallel,2}
v_{\parallel} = v_{\parallel,1} - v_{\parallel,2}
s
s_{\parallel} = v_{\parallel} + r_{\parallel}
\xi(r)
\xi(s_\perp, s_\parallel)
Probability of finding a pair of galaxies at distance r
Virial motions within halos
v_{\parallel,1}
v_{\parallel,2}
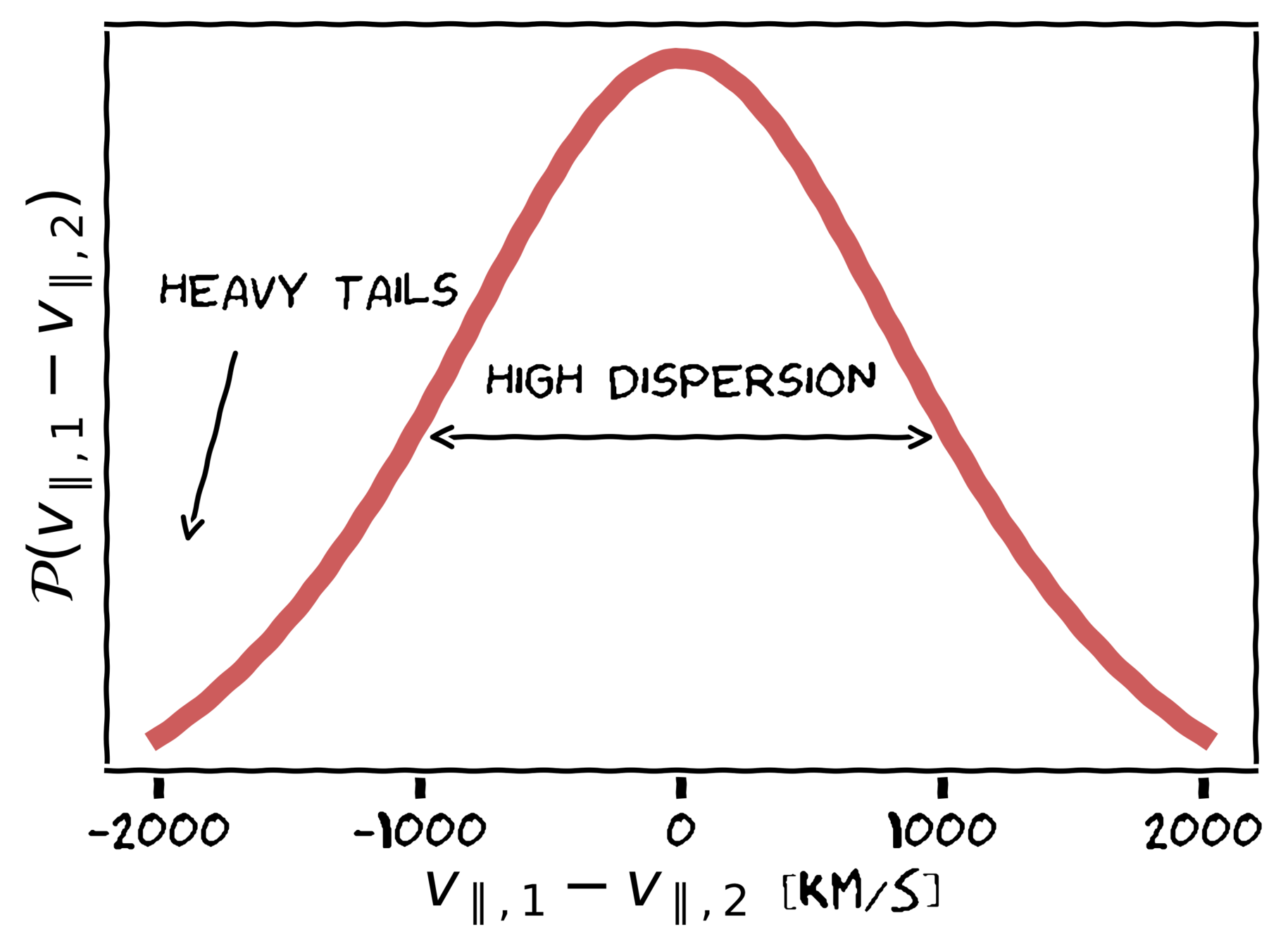
Infall towards halos
v_{\parallel,1}
v_{\parallel,2}
1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \xi^R(r)\right) \red{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
\xi^S(s_\perp, s_\parallel) \approx \xi^R(s) + \sum_n \frac{(-1)^n}{n!} \frac{d^n}{d s_\parallel^n} \left( (1+ \xi^R(s)) m_n(s) \right)
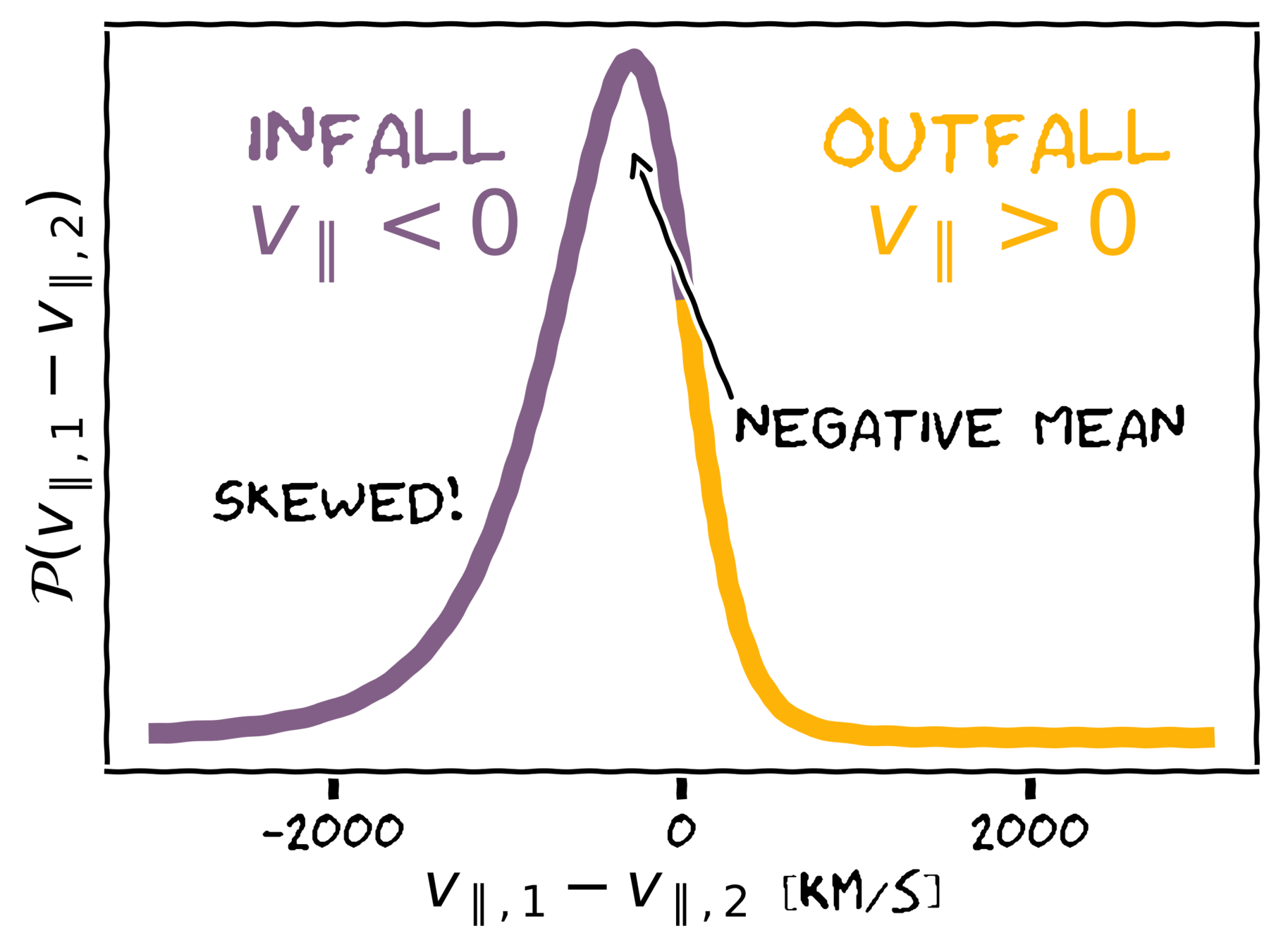
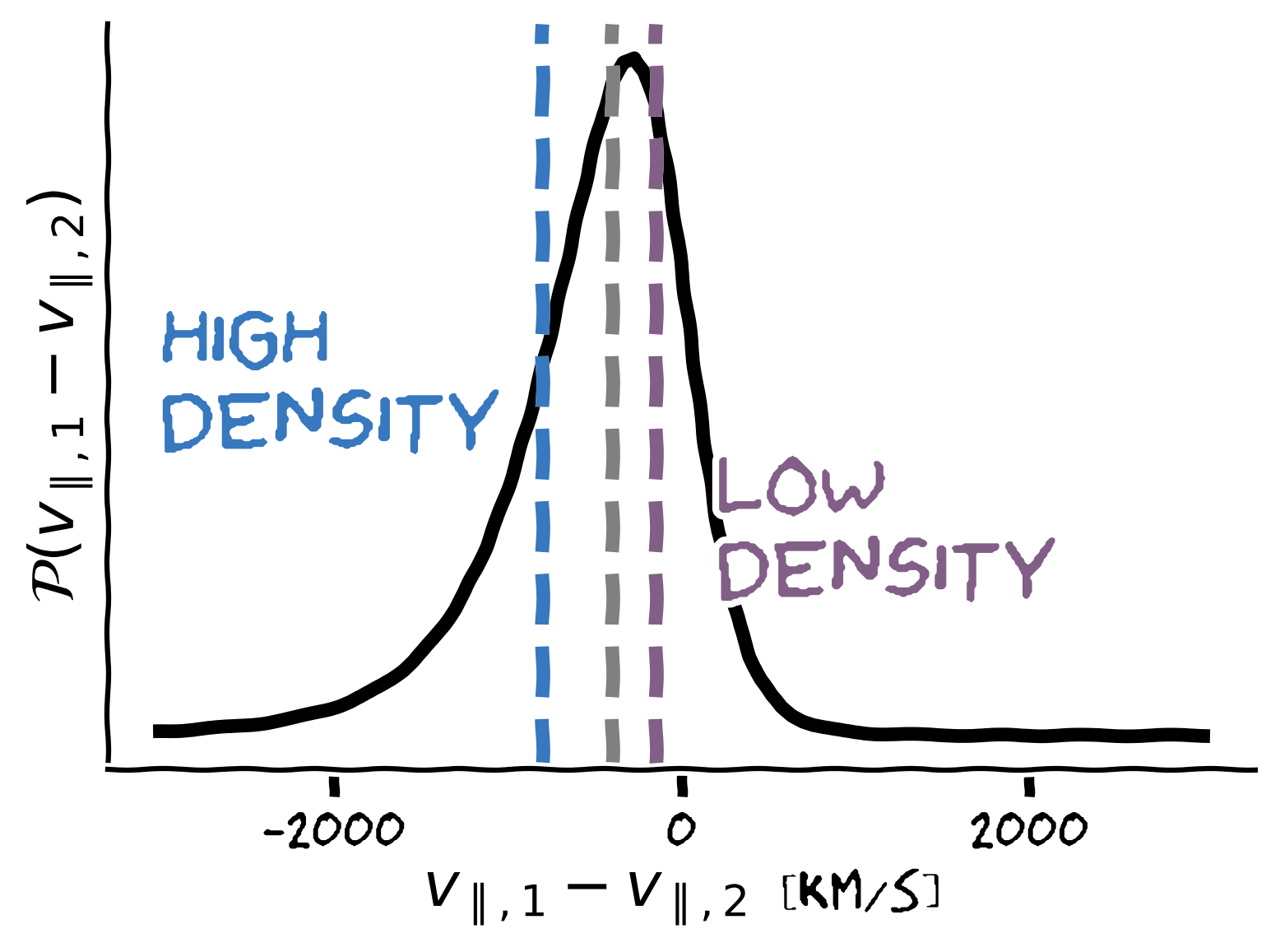
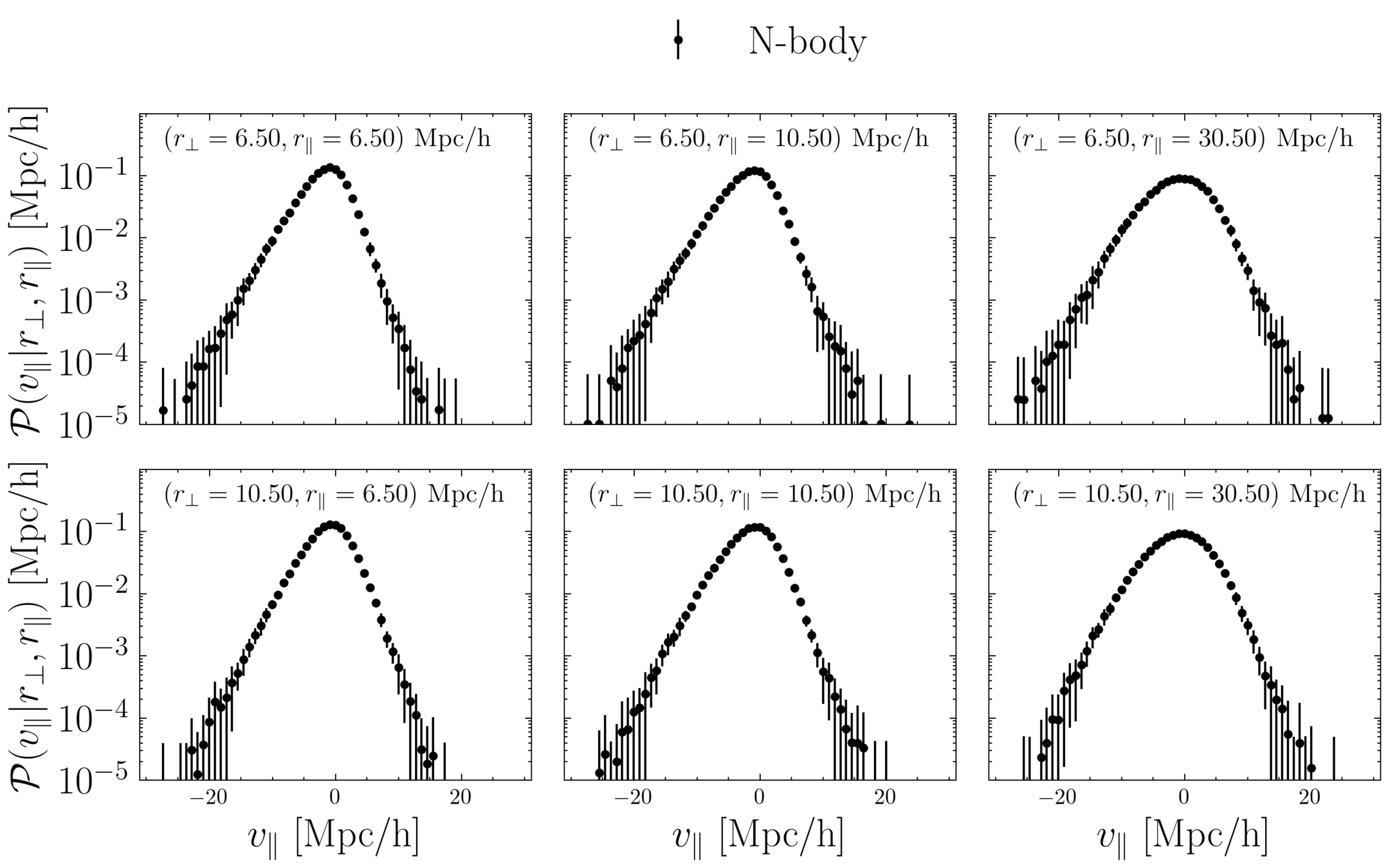
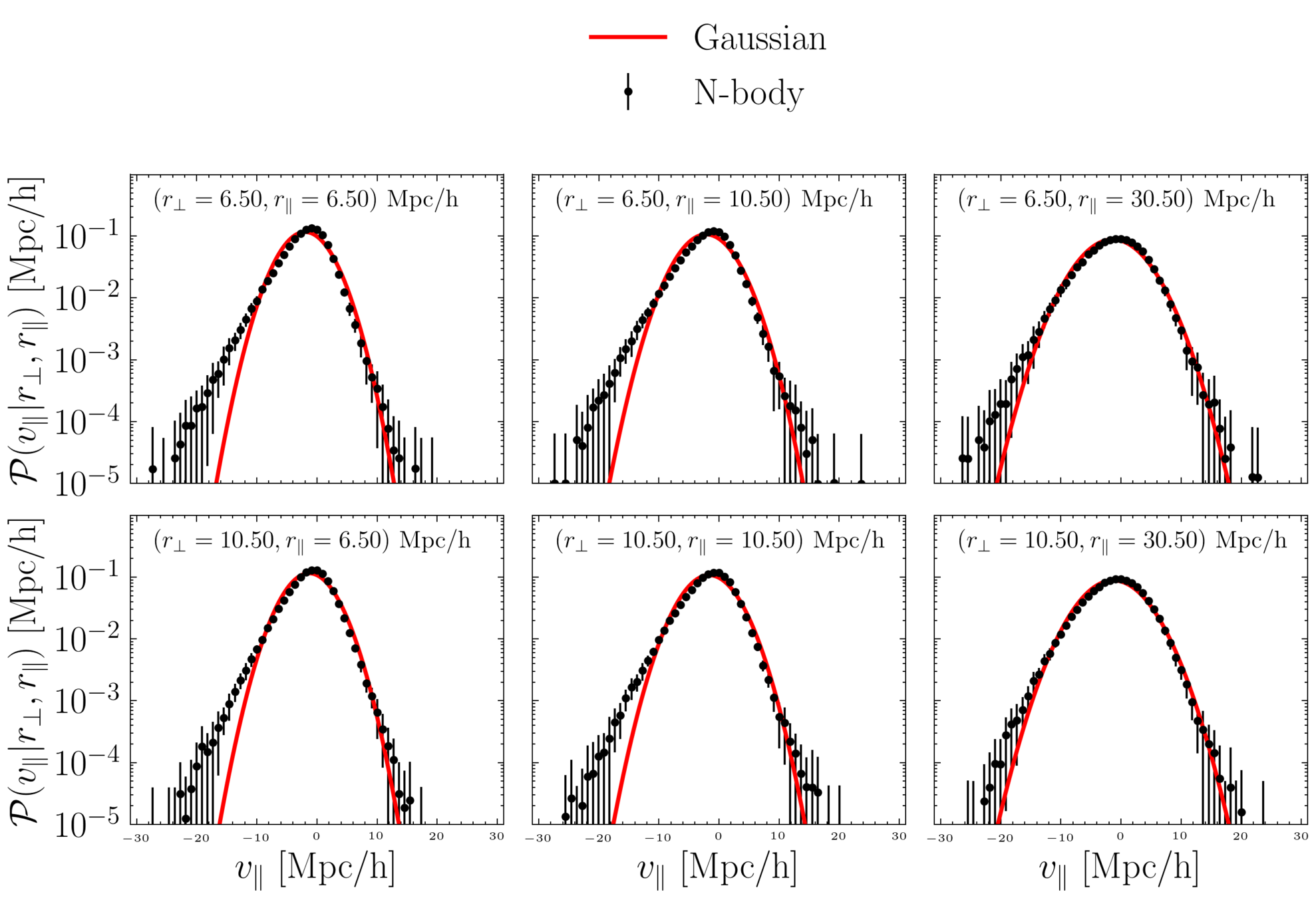
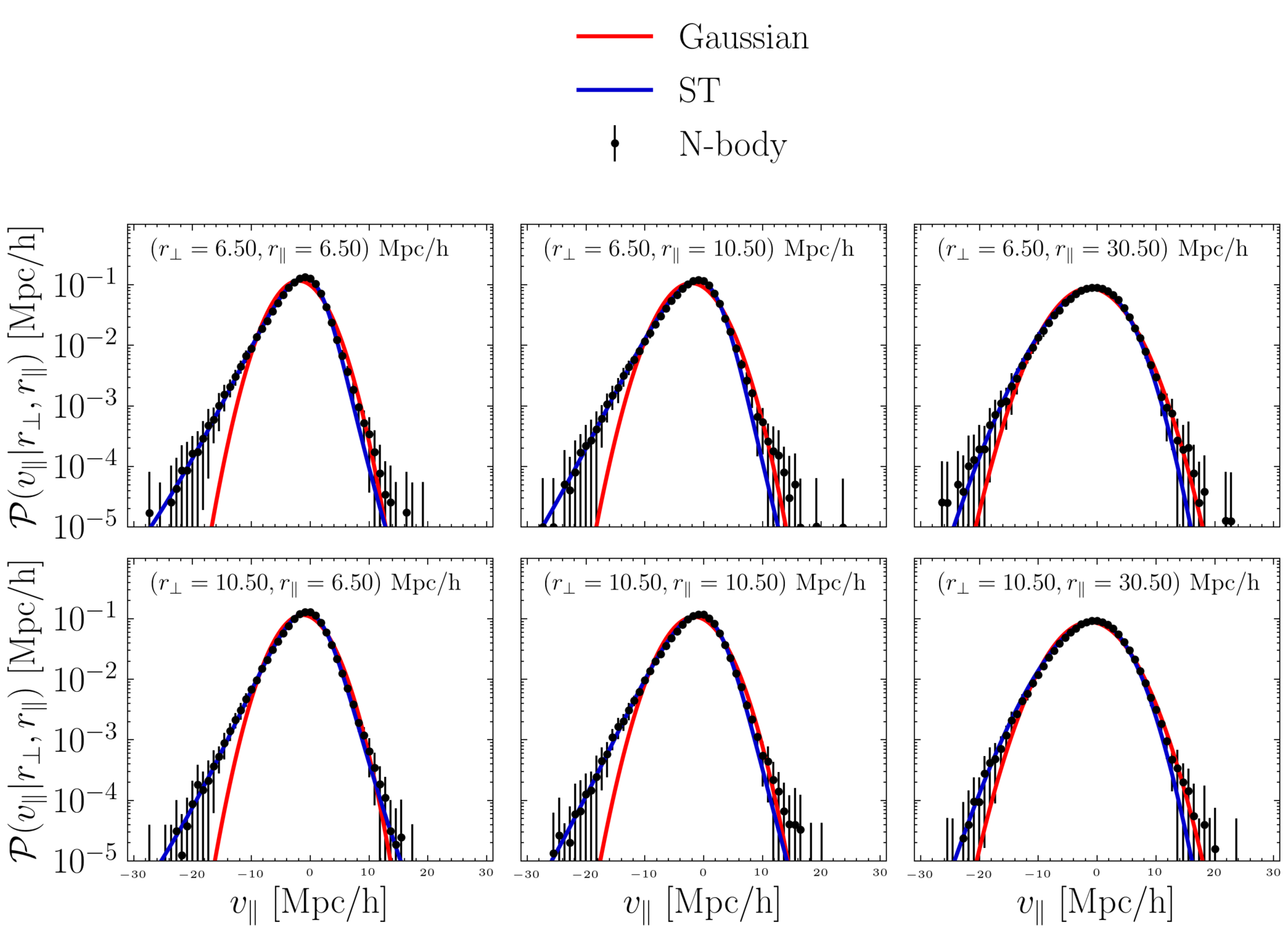
On large scales,
slowly varying function of
r_\parallel
n = 4 reproduces clustering down to small scales
v_\parallel < 0
INFALL
v_\parallel > 0
OUTFLOW
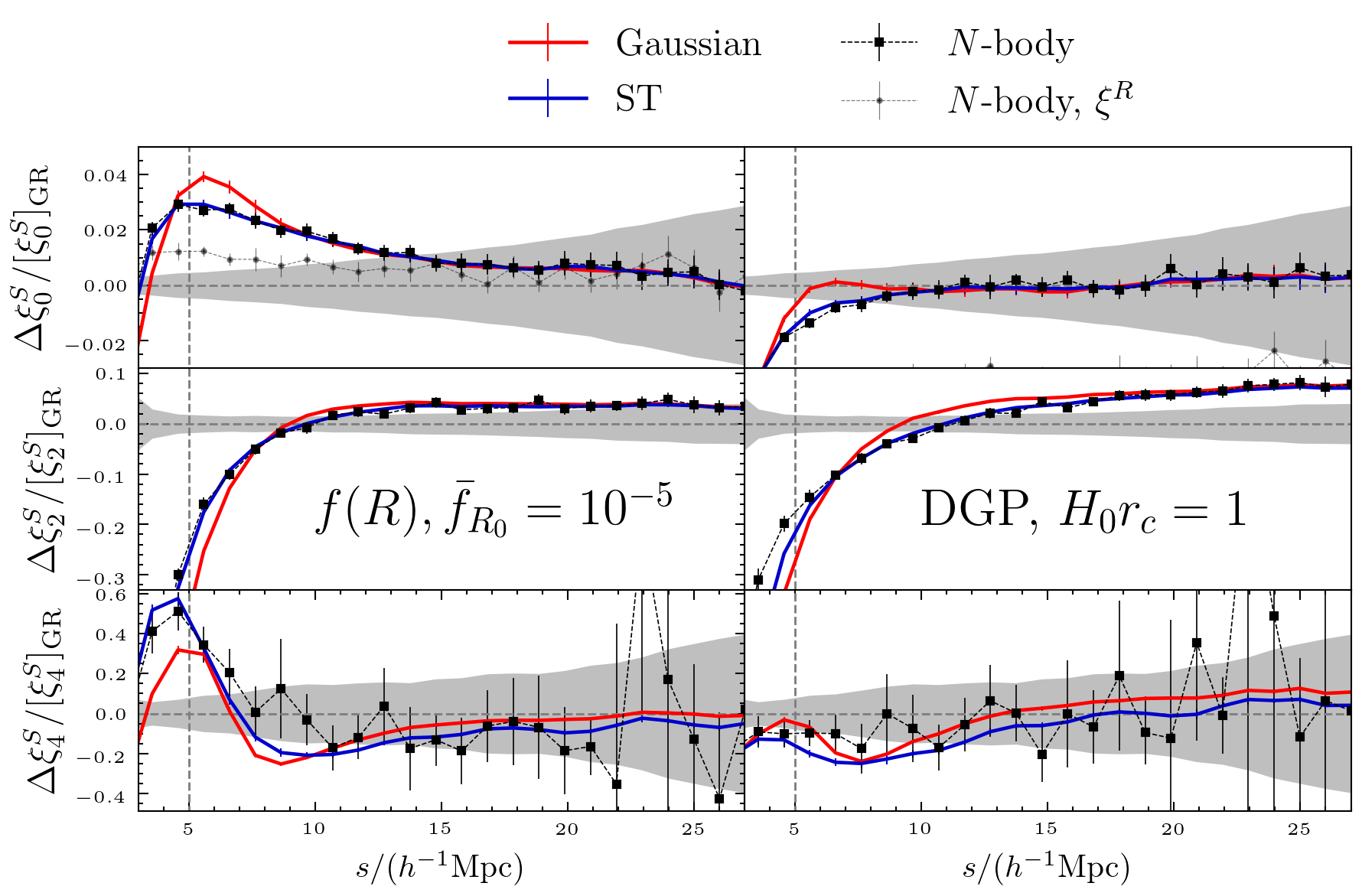
Two representative extensions to General Relativity:
- The background expansion is the same as LCDM
- One parameter to describe deviations from LCDM
1+\xi^S(s_\perp, s_\parallel) = \int dr_\parallel \left(1 + \bold{\xi^R(r)}\right) \bold{\mathcal{P}(v_\parallel=s_\parallel-r_\parallel|r_\perp, r_\parallel)}
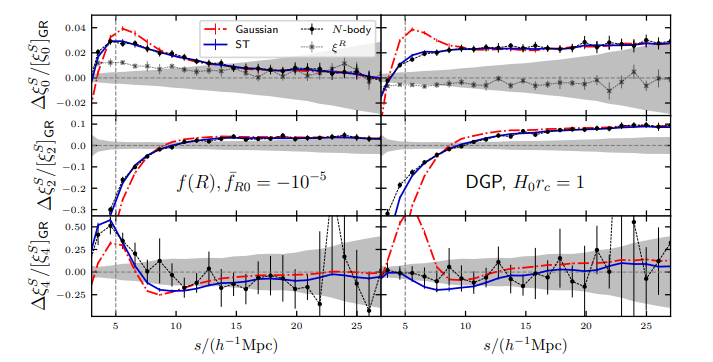
How do these vary with cosmological parameters on small scales?
Described by four parameters
\xi_{hh}^S = \red{F}(\blue{\xi_{hh}^R(r|\vec{c})}, \blue{v^{i}_{hh}(r|\vec{c})})
\xi_{gg} \propto \int d M_h W(\vec{g}_j, M_h) \xi_{hh}(M_h)
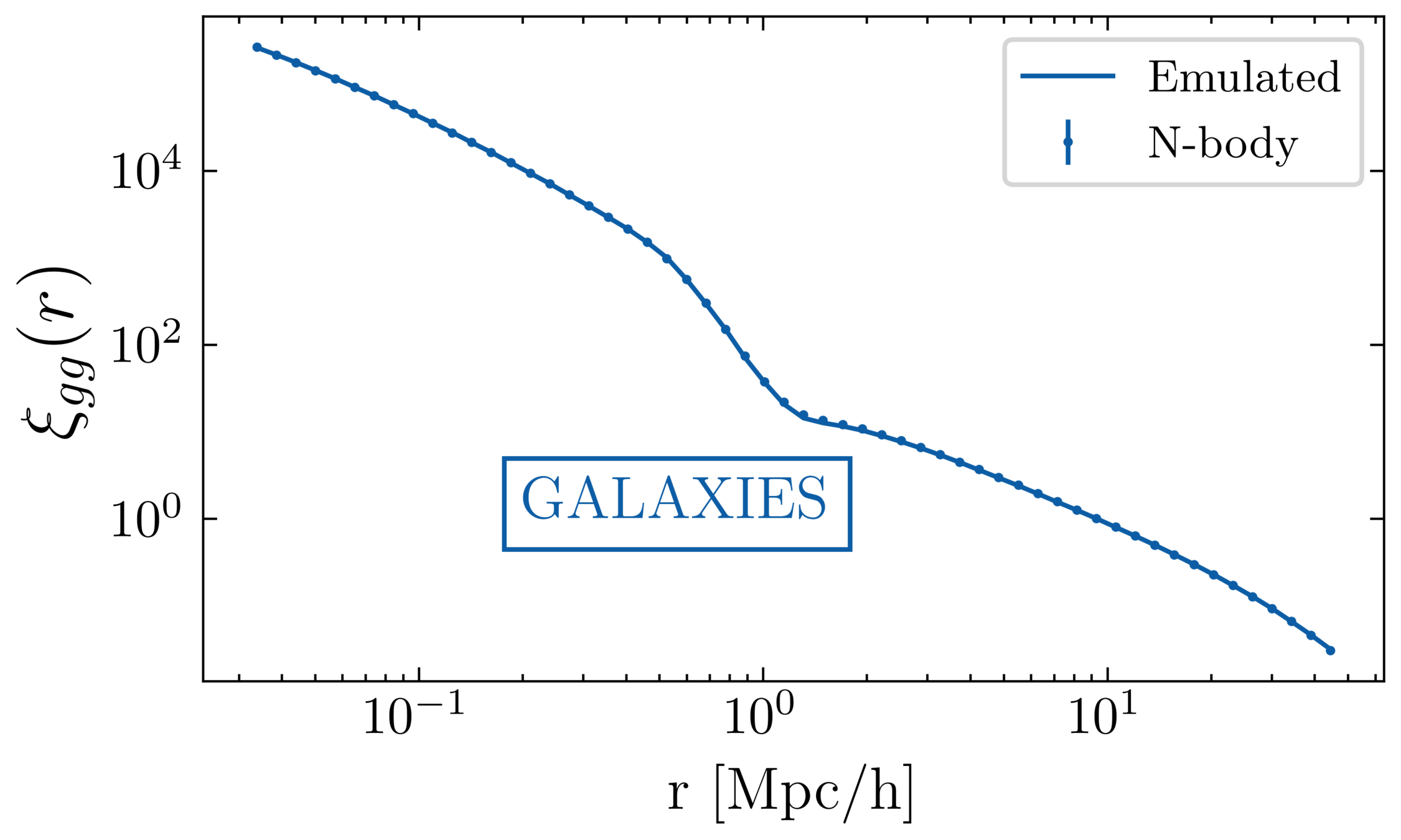
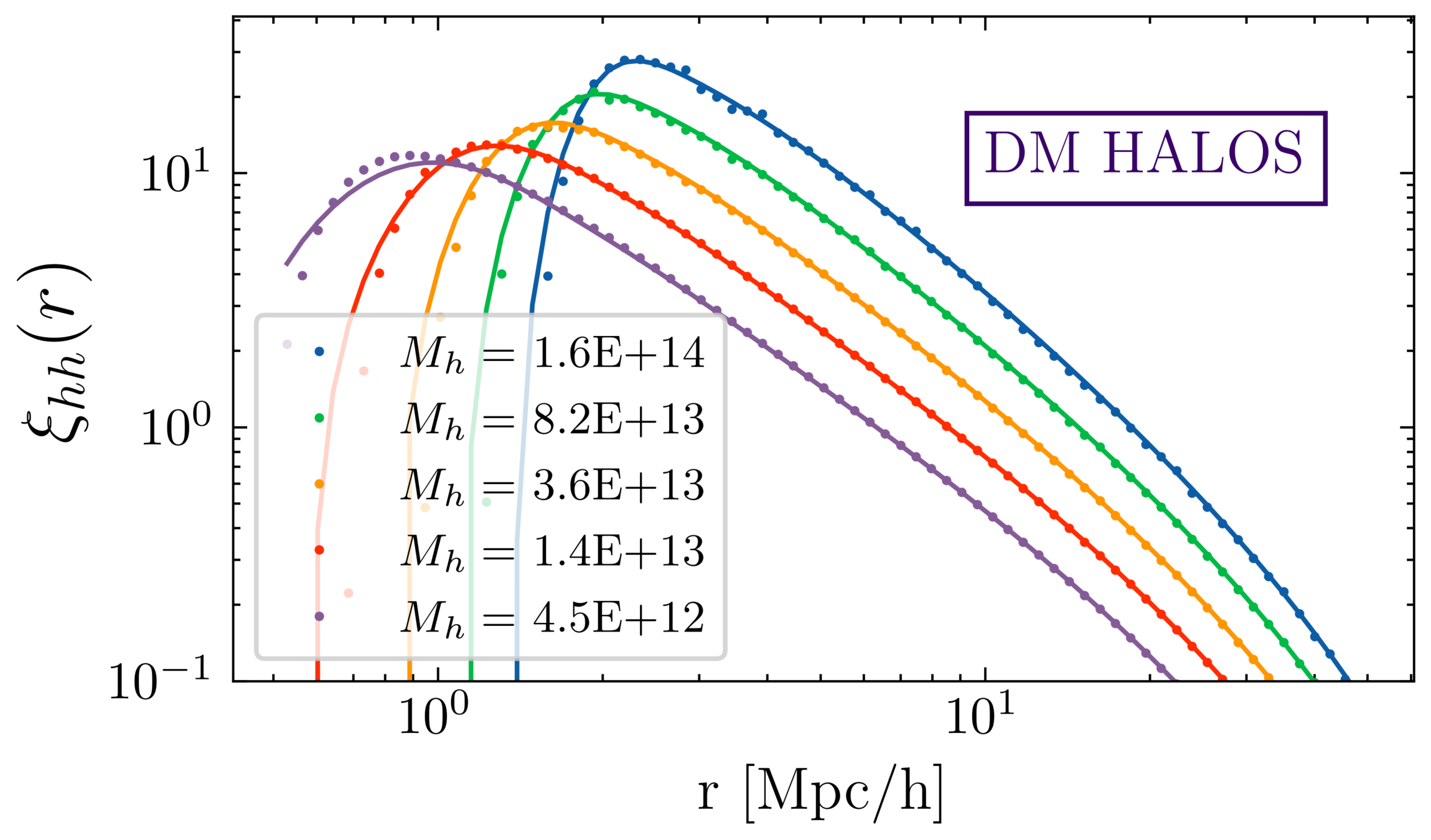
Code available on github soon!
\mathcal{O}(10^6)
Likelihood evaluations
w_c
lnAs
\Omega_\Lambda
lnAs
\Omega_\Lambda
r_\mathrm{min} = 1 \, h^{-1} \mathrm{Mpc}
r_\mathrm{min} = 10 \, h^{-1} \mathrm{Mpc}
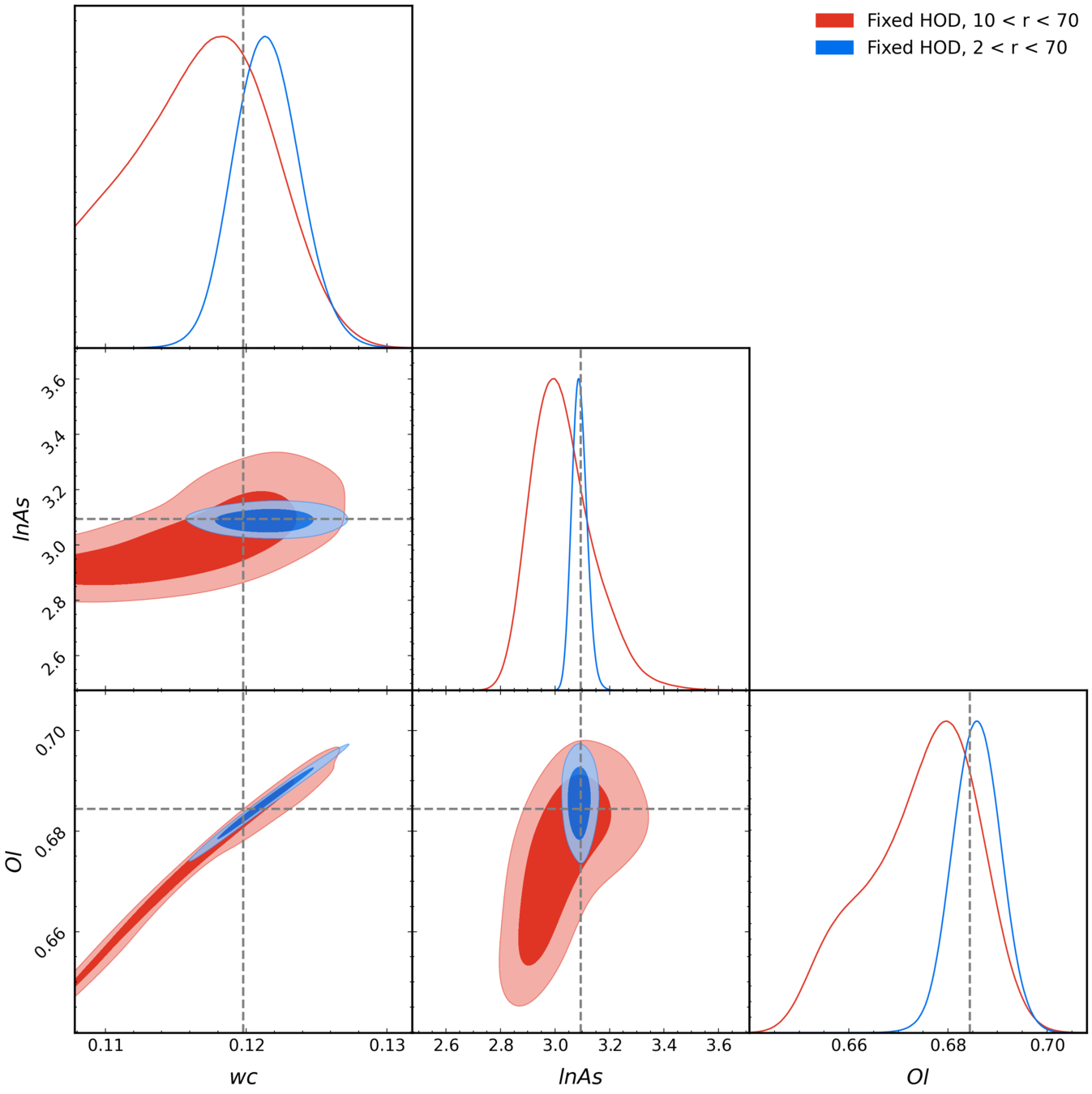
But... How much information are we ignoring??
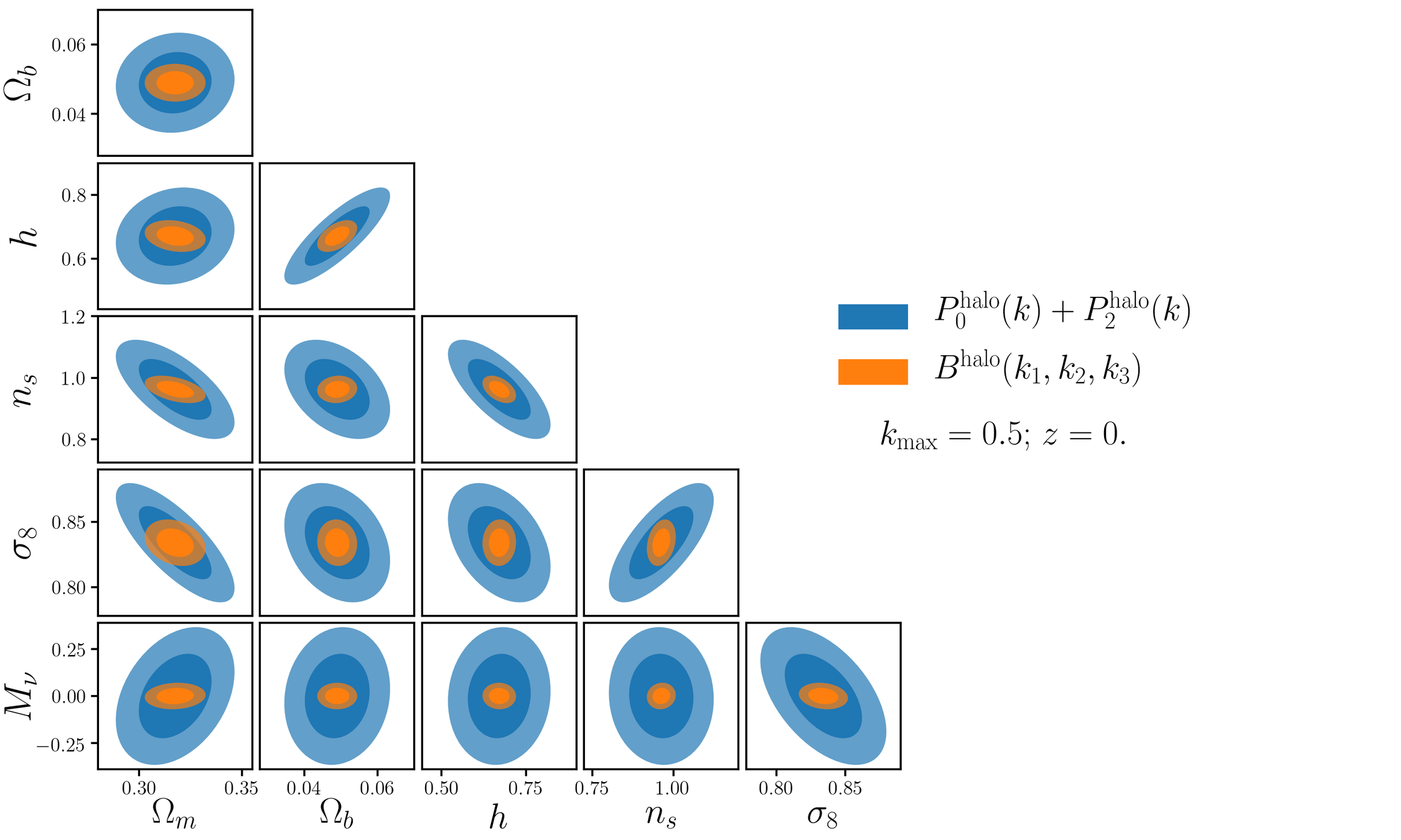
Credit: ChangHoon Hahn et al https://arxiv.org/abs/2012.02200
P
B
P(k)
B(k_1,k_2,k_3)
r
r1
r2
r3
Credit: Sihao Cheng et al https://arxiv.org/pdf/2006.08561.pdf
\Omega_M
\Omega_\Lambda
\sigma_8
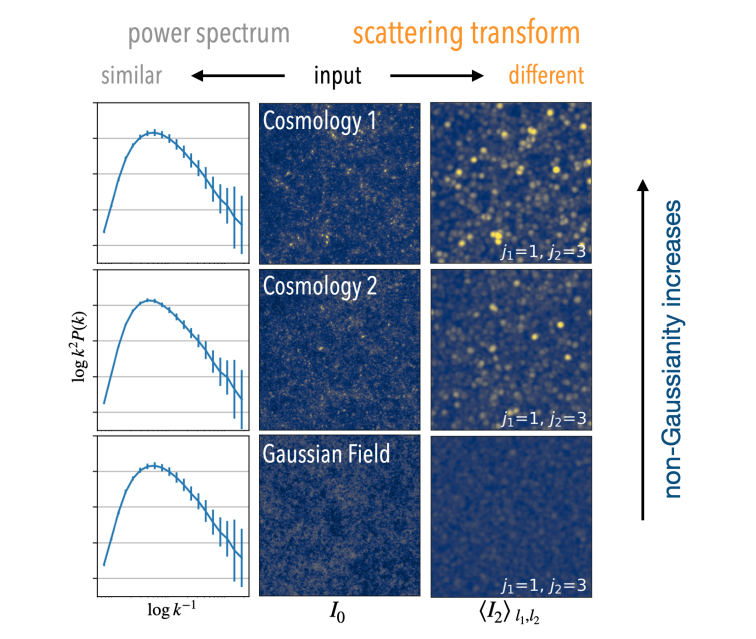
Input
x
Neural network
f
Representation
(Summary statistic)
r = f(x)
Output
o = g(r)
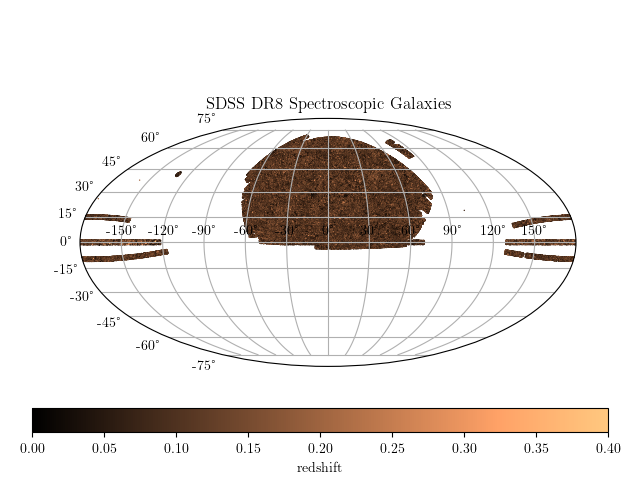
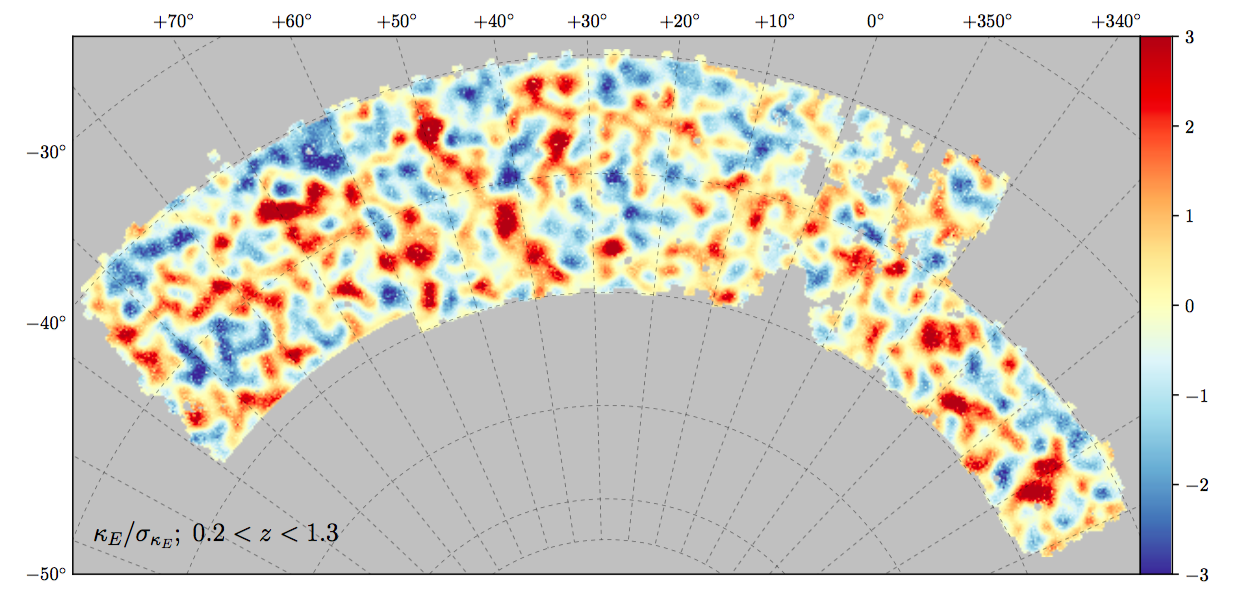
Increased interpretability through structured inputs
Modelling cross-correlations
ML and cosmology
- ML to accelerate non-linear predictions: allow MCMC sampling of non-linear scales
- Precision of future surveys: what and how we emulate will have a big impact on cosmological constraints
- Can ML extract **all** the information that there is at the field-level in the non-linear regime?
- Compare data and simulations, point us to the missing pieces?
deck
By carol cuesta
