Graphics Programming Virtual Meetup
Discord
Tiny Renderer
Software Rasterizer
Lessons 0-2
Following SSloy's Tutorial
My reference implementation
Lesson 0
Setup
Project Setup
- Needs`tgaimage.h` header
- Then copy-paste code
#include "tgaimage.h"
const TGAColor white = TGAColor(255, 255, 255, 255);
const TGAColor red = TGAColor(255, 0, 0, 255);
int main(int argc, char** argv)
{
TGAImage image(100, 100, TGAImage::RGB);
image.set(52, 41, red);
// i want to have the origin at the left bottom corner of the image
image.flip_vertically();
image.write_tga_file("output.tga");
return 0;
}Output (scaled up)
Lesson 1
Bresenham’s Line Drawing Algorithm
First Attempt
void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color)
{
// step size of 0.1
for (float t = 0.; t < 1.; t += .01)
{
// linearly interpolate between x0 & x1 and y0 & y1
int x = x0 + (x1 - x0) * t;
int y = y0 + (y1 - y0) * t;
image.set(x, y, color);
}
}Simply iterate "along" the line segment, turning on pixels as you go over them
Issues
- Only takes 100 steps
- Leaves gaps!
- No aliasing
line(-100, -100, 500, 500, image, white);
Second Attempt
void line(int x0, int y0, int x1, int y1, TGAImage& image, TGAColor color)
{
//increment X by one every step
for (int x = x0; x <= x1; x++)
{
// get the current distance we are from x0 to x1 on a range of 0 to 1
float t = (x - x0) / (float)(x1 - x0);
// linearly interpolate y using that value between 0 to 1
int y = y0 * (1. - t) + y1 * t;
image.set(x, y, color);
}
}Have a step size of 1 pixel on the x axis, then linearly interpolate for the y axis
Better?
- Doesn't account for y axis!
- If the line goes down faster than it goes over , the y axis needs to take many steps but the x only takes one.
- We can do better!
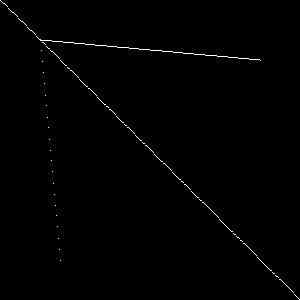
line(-100, -100, 500, 500, image, white);
line(40, 40, 60, 260, image, white);
line(40, 40, 260, 60, image, white);Attempt 3
if (std::abs(x0-x1)<std::abs(y0-y1)) {
std::swap(x0, y0);
std::swap(x1, y1);
steep = true;
}
}Solution: Choose the steeper axis and iterate on that
Find the larger delta and make "X" represent that
Account for 'negative direction'
if (x0 > x1) { // make it left−to−right
std::swap(x0, x1);
std::swap(y0, y1);
}Now "X" is just which ever was the steeper axis
for (int x = x0; x <= x1; x++) {
float t = (x - x0) / (float)(x1 - x0);
int y = y0 * (1. - t) + y1 * t;
if (steep) {
image.set(y, x, color); // if transposed, de−transpose
} else {
image.set(x, y, color);
}
}Much better!
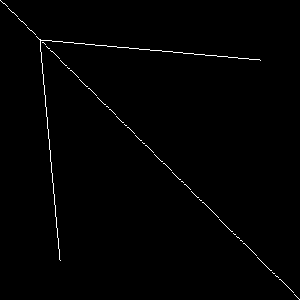
Attempt-4
- Factor out repeated calculations
- `derrer` is the slope
- Used to update the non major axis
- `error` is an accumulator
int dx = x1 - x0;
int dy = y1 - y0;
float derror = std::abs(dy / float(dx));
float error = 0;
int y = y0;- Modify for loop
- Remove linear interpolation calculation every iteration
- Update off-axis value if `error` > 0.5
- and reset accumulator
for (int x = x0; x <= x1; x++) {
if (steep) {
image.set(y, x, color);
} else {
image.set(x, y, color);
}
error += derror;
if (error > .5) {
//make sure we increment in the 'right' direction
y += (y1 > y0 ? 1 : -1);
error -= 1.;
}
}
Fixed Diagonal issues!
Attempt 5
- Remove floating point entirely
- Do this by changing the scale of `error` and `derror`
- Use minor axis difference instead of raw 'slope'
int dx = x1 - x0;
int dy = y1 - y0;
int derror2 = std::abs(dy) * 2;
int error2 = 0;
int y = y0;
for (int x = x0; x <= x1; x++) {
if (steep) {
image.set(y, x, color);
} else {
image.set(x, y, color);
}
error2 += derror2;
if (error2 > dx) {
y += (y1 > y0 ? 1 : -1);
error2 -= dx * 2;
}
}Wireframe Rendering
Must load the `.obj` models first
Copy-Paste `model.h` `model.cpp` and `geometry.h` into the project
Model model{"obj/african_head.obj"};
TGAImage image(width, height, TGAImage::RGB);
for (int i = 0; i < model.nfaces(); i++) {
std::vector<int> face = model.face(i);
for (int j = 0; j < 3; j++) {
Vec3f v0 = model.vert(face[j]);
Vec3f v1 = model.vert(face[(j + 1) % 3]);
int x0 = (v0.x + 1.) * width / 2.;
int y0 = (v0.y + 1.) * height / 2.;
int x1 = (v1.x + 1.) * width / 2.;
int y1 = (v1.y + 1.) * height / 2.;
line(x0, y0, x1, y1, image, white);
}
}
Lesson 2
Triangle Rasterization & back face culling
Line Sweep Algorithm
- Sort vertices of the triangle by their y-coordinates
- Rasterize simultaneously the left and the right sides of the triangle
- Draw a horizontal line segment between the left and the right boundary points
implementation
void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
// sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!)
if (t0.y>t1.y) std::swap(t0, t1);
if (t0.y>t2.y) std::swap(t0, t2);
if (t1.y>t2.y) std::swap(t1, t2);
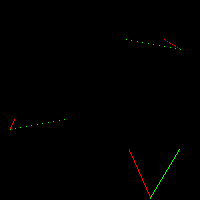
line(t0, t1, image, green);
line(t1, t2, image, green);
line(t2, t0, image, red);
}
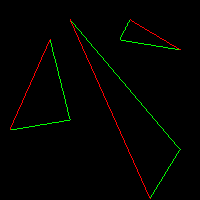
Issue
- There are 'two' green lines for each red
- Can't easily sweep left to right
- Solution: Split red into two lines, create 2 subtriangles
- Second triangle is rendered here
void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) {
// sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!)
if (t0.y>t1.y) std::swap(t0, t1);
if (t0.y>t2.y) std::swap(t0, t2);
if (t1.y>t2.y) std::swap(t1, t2);
int total_height = t2.y-t0.y;
for (int y=t0.y; y<=t1.y; y++) {
int segment_height = t1.y-t0.y+1;
float alpha = (float)(y-t0.y)/total_height;
float beta = (float)(y-t0.y)/segment_height;
Vec2i A = t0 + (t2-t0)*alpha;
Vec2i B = t0 + (t1-t0)*beta;
if (A.x>B.x) std::swap(A, B);
for (int j=A.x; j<=B.x; j++) {
image.set(j, y, color); // attention, due to int casts t0.y+i != A.y
}
}
for (int y=t1.y; y<=t2.y; y++) {
int segment_height = t2.y-t1.y+1;
float alpha = (float)(y-t0.y)/total_height;
float beta = (float)(y-t1.y)/segment_height;
Vec2i A = t0 + (t2-t0)*alpha;
Vec2i B = t1 + (t2-t1)*beta;
if (A.x>B.x) std::swap(A, B);
for (int j=A.x; j<=B.x; j++) {
image.set(j, y, color); // attention, due to int casts t0.y+i != A.y
}
}
}
Final Output
Is there a better way?
- Line-sweep works for monolithic processors
- Modern hardware isn't a single core
- Determine if a pixel is within a triangle
- Then shade it accordingly
Possible psuedo code
triangle(vec2 points[3]) {
vec2 bbox[2] = find_bounding_box(points);
for (each pixel in the bounding box) {
if (inside(points, pixel)) {
put_pixel(pixel);
}
}
}Barycentric Coordinates
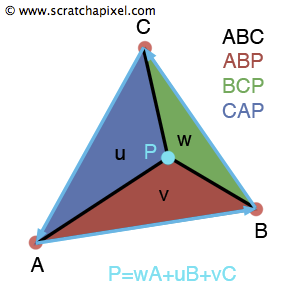
- Given a triangle ABC and a point P
- The coordinates of P with respect to ABC
P = (1 - u - v)A + uB + vC
Point P has coordinates (u,v) in the basis A, AB, and AC
P = A + u\overrightarrow{AB} + v\overrightarrow{AC}
A barycentric coordinate system (in 2D) is when the location of a point is specified by reference to a triangle's vertices.
Rearrange
u\overrightarrow{AB} + v\overrightarrow{AC} + \overrightarrow{PA} = 0
Linear System of Equations
\begin{Bmatrix}
u\overrightarrow{AB}_x + v\overrightarrow{AC}_x + \overrightarrow{PA}_x = 0 \\
u\overrightarrow{AB}_y + v\overrightarrow{AC}_y + \overrightarrow{PA}_y = 0
\end{Bmatrix}
Rewrite in matrix form
\begin{Bmatrix}
\begin{bmatrix} u & v & 1 \end{bmatrix} & \begin{bmatrix} \overrightarrow{AB}_x \\ \overrightarrow{AC}_x \\ \overrightarrow{PA}_x \end{bmatrix} = 0\\
\begin{bmatrix} u & v & 1 \end{bmatrix} & \begin{bmatrix} \overrightarrow{AB}_y \\ \overrightarrow{AC}_y \\ \overrightarrow{PA}_y \end{bmatrix} = 0
\end{Bmatrix}
- Want a vector (u,v,1) which is orthogonal to both (ABx,ACx,PAx) and (ABy,ACy,PAy)
- To find an intersection of two straight lines in a plane, it is sufficient to compute the cross product.
Vec3f barycentric(Vec2i *pts, Vec2i P)
{
Vec3f u = cross(
Vec3f(pts[2][0] - pts[0][0], pts[1][0] - pts[0][0], pts[0][0] - P[0]),
Vec3f(pts[2][1] - pts[0][1], pts[1][1] - pts[0][1], pts[0][1] - P[1]));
/* `pts` and `P` has integer value as coordinates
so `abs(u[2])` < 1 means `u[2]` is 0, that means triangle is degenerate
in this case return something with negative coordinates */
if (std::abs(u[2]) < 1) return Vec3f(-1, 1, 1);
return Vec3f(1.f - (u.x + u.y) / u.z, u.y / u.z, u.x / u.z);
}void triangle(Vec2i *pts, TGAImage &image, TGAColor color) {
Vec2i bboxmin(image.get_width()-1, image.get_height()-1);
Vec2i bboxmax(0, 0);
Vec2i clamp(image.get_width()-1, image.get_height()-1);
for (int i=0; i<3; i++) {
for (int j=0; j<2; j++) {
bboxmin[j] = std::max(0, std::min(bboxmin[j], pts[i][j]));
bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j], pts[i][j]));
}
}
Vec2i P;
for (P.x=bboxmin.x; P.x<=bboxmax.x; P.x++) {
for (P.y=bboxmin.y; P.y<=bboxmax.y; P.y++) {
Vec3f bc_screen = barycentric(pts, P);
// if P is > (0,0,0), then P is withing the triangle
if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue;
image.set(P.x, P.y, color);
}
}
} Plug into psuedocode
Tada!
Lets Draw a model instead
We'll use random colors too
for (int i = 0; i < model.nfaces(); i++) {
std::vector<int> face = model.face(i);
vec2 screen_coords[3];
for (int j = 0; j < 3; j++) {
vec3 world_coords = model.vert(face[j]);
screen_coords[j] =
vec2((world_coords.x + 1.) * width / 2.,
(world_coords.y + 1.) * height / 2.);
}
triangle(screen_coords, image,
TGAColor(rand() % 255, rand() % 255, rand() % 255, 255));
}
Now to add shading & lighting
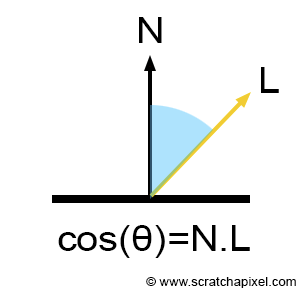
Simple lighting: Lambertian Reflectance
Or just Lamberts cosine law
for (int i=0; i<model->nfaces(); i++) {
std::vector<int> face = model->face(i);
Vec2i screen_coords[3];
Vec3f world_coords[3];
for (int j=0; j<3; j++) {
Vec3f v = model->vert(face[j]);
screen_coords[j] = Vec2i((v.x+1.)*width/2., (v.y+1.)*height/2.);
world_coords[j] = v;
}
Vec3f n = (world_coords[2]-world_coords[0])^(world_coords[1]-world_coords[0]);
n.normalize();
float intensity = n*light_dir;
// Negative direction means lighting is behind the polygon
// Allows very simple version of backface culling
if (intensity>0) {
triangle(screen_coords, image,
TGAColor(intensity*255, intensity*255, intensity*255, 255));
}
}
Graphics Programming Virtual Meetup
TinyRenderer Lesson 0-2
By Charles Giessen
