Теоремы, которые меняют мир: от компиляторов до экономики
Александр Грызлов
Программист-исследователь
IMDEA Software Institute
Peredelanoconf
25/01/2025
О себе
- Работаю программистом с 2005 года
- Осциллирую между индустрией и академией
- Занимался бэкендом, дата инжинирингом, биоинформатикой
- Последние 5 лет: пруф-инжиниринг
- Корректность программ и алгоритмов
План
- Равенства, порядки и вычисления
- Aвтоматизация мышления
-
От программ к сложным системам
Часть 1
Равенства, порядки и вычисления
Равенство
может быть
тривиально однозначным:
A = A 5+2 = 7
структурным:
{1,2,3} = {3,1,2}
неочевидным:
quicksort(xs) = mergesort(xs)
Неравенство
А "вложено в" или "предшествует" B
A ≤ B ⇔ ∃X,B = A+X
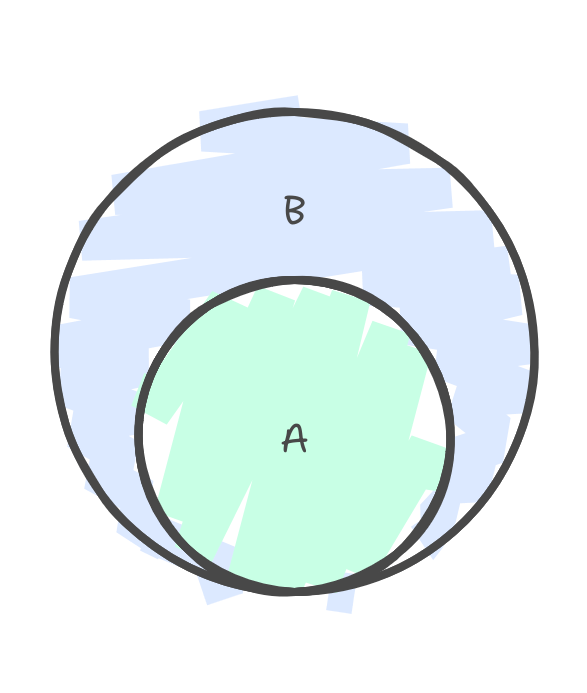
A и B могут быть преобразованы друг в друга
A=B ⇔ A ≤ B ≤ A
Порядки и программы
Идея порядка вездесуща
в программировании и математике:
- следствие
- причинность
- преобразование
A → B ~ A ≤ B
Теорема о структурированных программах
aka Бёма-Якопини (1966)
Любую программу можно разбить на 3 управляющие структуры:
1. последовательное выполнение
2. ветвление
3. цикл
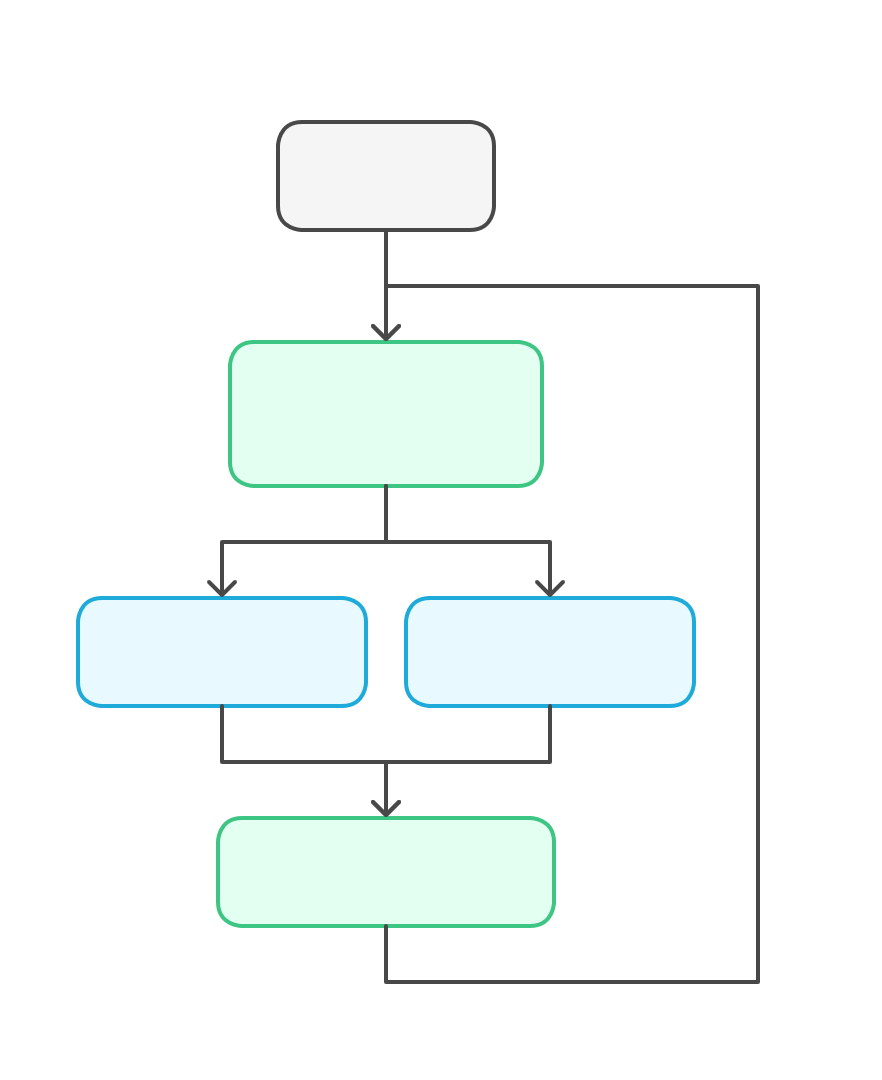
Порядок программ
Программа накапливает информацию, двигаясь вперед по переходам и производя ветвления
Циклы (или рекурсия) дают нам автоматизацию, но и делают рассуждения о программах сложнее
Можем ли мы всегда гарантировать что программа не впадает в бесконечный цикл?
Нет! Задача остановки, Тьюринг (1936)

Неподвижная точка
Математически вычисление программы с циклом эквивалентно нахождению неподвижной точки
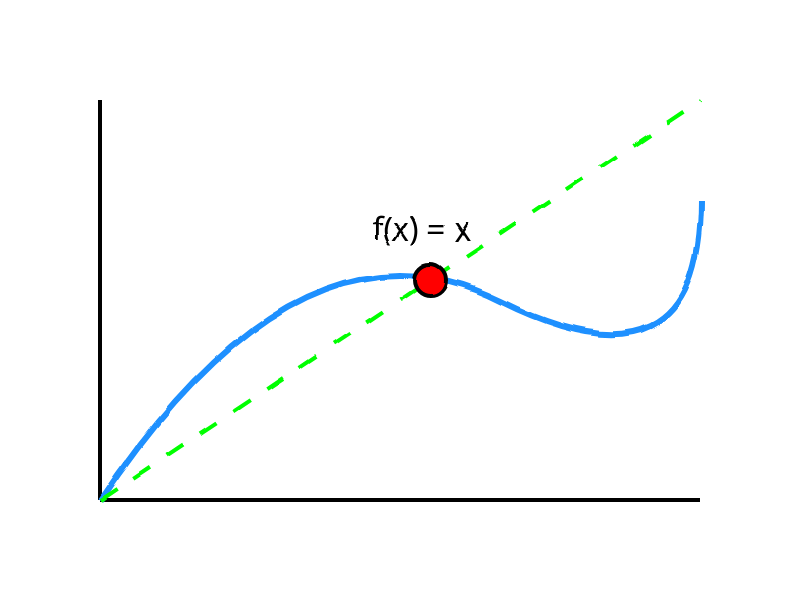

f

Теорема о неподвижной точке
aka Кнастера-Тарского (1955)
Если f "не теряет" информацию (монотонна)
и порядок не имеет "петель",
то неподвижная точка существует всегда
Заменив "естественный" порядок программы на "хорошее" приближение, мы можем узнать свойства программы, не запуская её целиком
Пример приближения
Игрушечный язык с if, рекурсией и целыми числами:
fact(x) =
if lte(x, 1) then 1
else x * fact(x - 1)
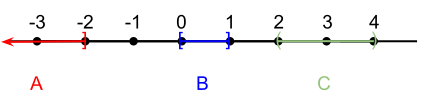
Порядок его значений: ⊥ ≤ ... -1 ≤ 0 ≤ 1 ≤ ...
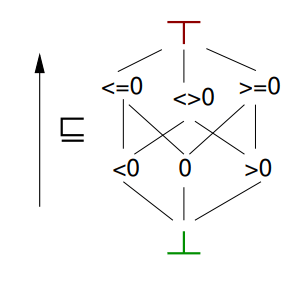
Сгруппируем их по знаку:
Статический анализ
Ключевой компонент оптимизирующих компиляторов и инструментов верификации


- анализ потоков данных
- анализ потоков управления
- анализ формы
- ...

Часть 2
Aвтоматизация мышления
Горький урок
Ричард Саттон, основатель обучения с подкреплением:
Главный урок, который можно извлечь из 70 лет исследований в сфере ИИ, состоит в том, что общие методы, максимально использующие вычисления, в конечном итоге оказываются наиболее эффективными, причем с большим отрывом. Главной причиной этого является закон Мура, а точнее, его обобщение о продолжающемся экспоненциальном падении стоимости единицы вычислений.
Поиск поиску рознь
- Подмена порядка для приблизительного поиска работает для очень широкого класса программ, но ценой выбора свойств вручную
- Можем ли мы использовать другие математические трюки для точного и автоматизированного поиска в более узких задачах?
Поиск в математике
- Компактность = у множества объектов
нет "потерянных точек"
- Вычислительно:
мы всегда можем найти объект множества
по его описанию
(X → Bool) → X
Теорема о компактности произведений
aka Тихонова (1935)
- Можно соединять компактные типы как лего
- Конструктор поисковых алгоритмов
p :: String -> Bool
p x = x == "password"
selectChar :: Ord r => J r Char
selectChar p = maxWith p ['a'..'z']
eightchars :: Ord r => [J r Char]
eightchars = replicate 8 selectChar
product :: [J r a] -> J r [a]
$ product eightchars p
> "password"Выполнимость
Классическая поисковая проблема:
булевая выполнимость (SATisfiability)
P ⇒ (Q ∧ ¬ R) P ∧ ¬ P

P ← true
Q ← true
R ← false
Теорема о NP-полноте SAT
aka Кука-Левина (1971-73)
задача SAT NP-полна
(т.е., в общем случае не может быть решена кроме как полным перебором)
- Более того, это первая задача, для которой была показана NP-полнота
- Несмотря на это, в 90х произошла так называемая SAT/SMT революция
SAT и теории
Булевая выполнимость удобна как фундамент
A ≤ B ⇔ ∃X,B = A+X- линейная арифметика
- ассоциативные массивы (
get/set) - ...
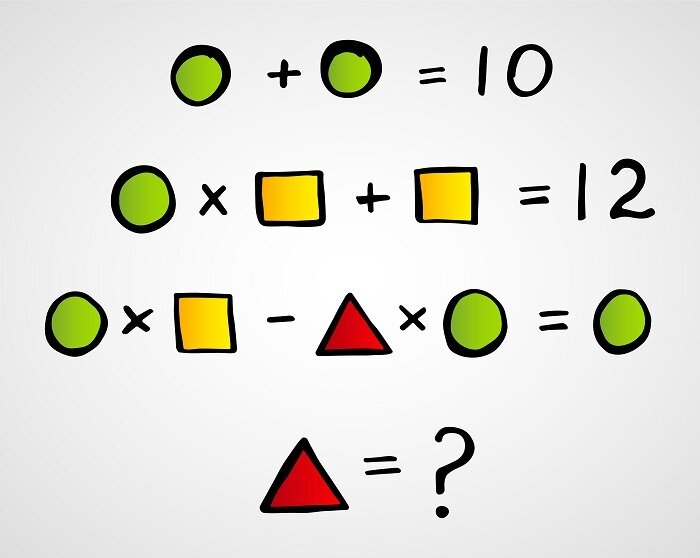
SAT/SMT как строительный блок
- Используя "универсальный решатель", мы можем строить более сложные алгоритмы, возвращаясь к идее неподвижных точек
- Классический статический анализ из 1 части хорошо работает на уже готовых программах
- Мы можем работать более гибко и интерактивно, проверяя сложные свойства для отдельных частей программы
- Технически, мы абстрагируем куски программы до проверяемых решателем свойств
Типы уточнения
{-@ elemAt :: xs:[a]
-> { i:Int | 0 <= i && i < len xs }
-> a @-}
elemAt :: [a] -> Int -> a
elemAt (x : _) 0 = x
elemAt (_ : xs) i = elemAt xs (i-1)
Часть 3
От программ к сложным системам
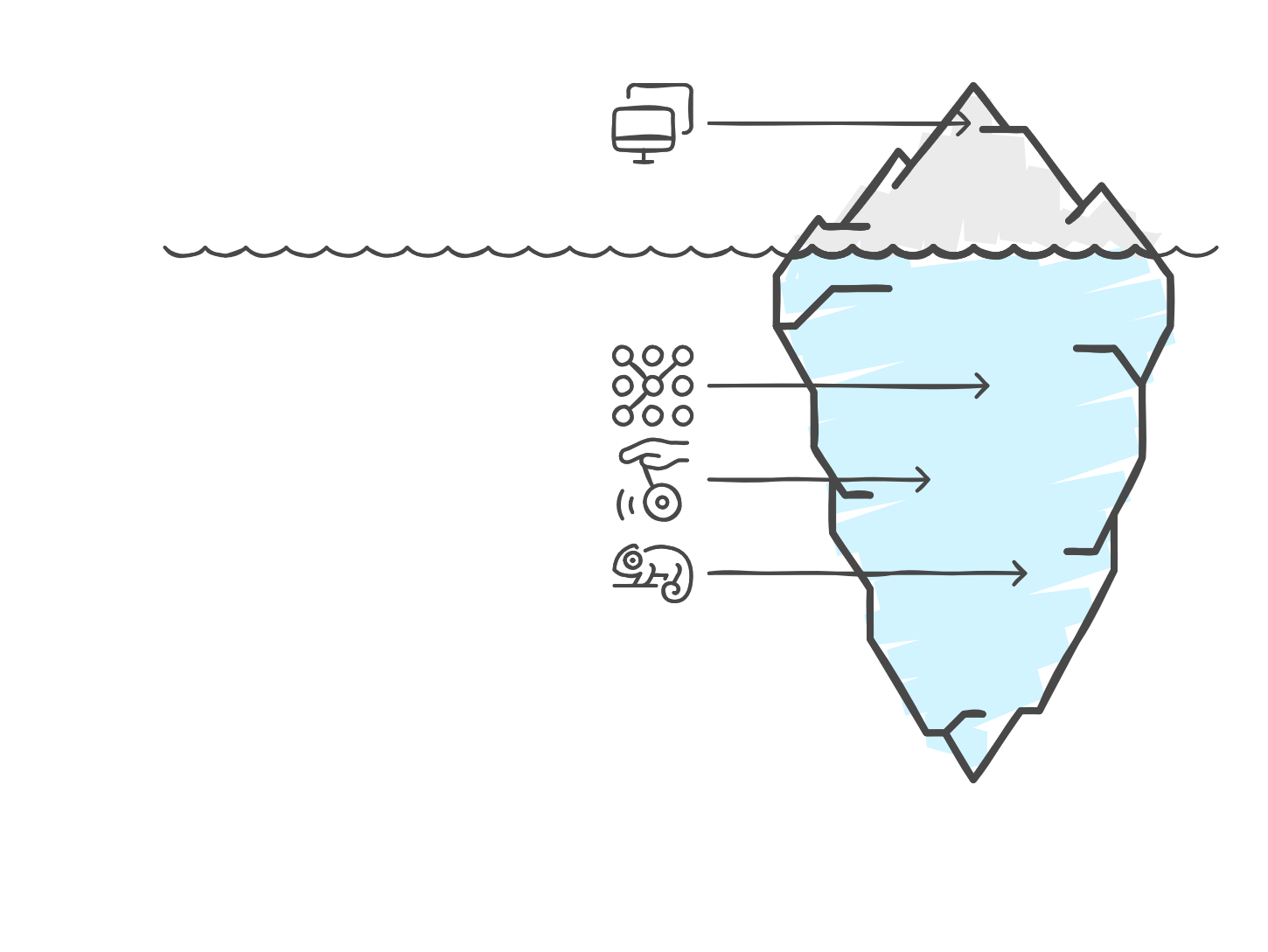
Усложняя программы
- Программы и задачи до этого были довольно абстрактны
- Анализ всё более сложных программ с эффектами (вероятности, многопоточность, ...)
- Анализ классов программ и моделей
Проверка моделей
Классическая сфера применения моделей - распределенные процессы и проектирование железа


Порядки в новых измерениях
Для программ со сложными спецификациями уже не хватает обычных порядков, нужна дополнительная структура
-
5 ≤ 7единственным образом -
"abba" → 2? -
"abba" → IO 2??
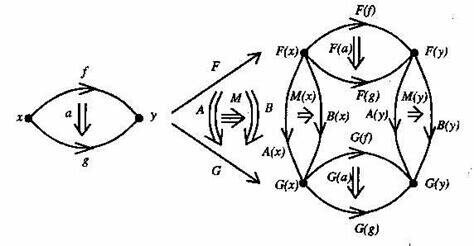
Категории
Квазипрограммы
- Цифровые и электрические схемы
- Финансовые протоколы
- Социальные механизмы (например, голосование)
- Игры
- Архитектуры машинного обучения
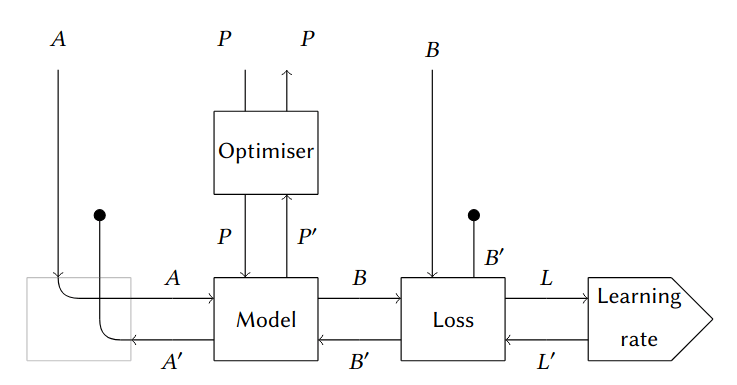
Сложные системы
часто двунаправлены!
Теорема о композиционности градиентного спуска
aka Фонга-Спивака-Туйераса (2017)
- можно сформировать данные для обучения отдельных элементов нейросети по отдельности
- можно создать алгоритм обратного распространения, чтобы разбить нейросеть на более сложные подструктуры, чем просто слои
backpropagation может применяться в более широком контексте, чем только к нейронным сетям
Киберкоты
Кибернетика aka теория управления
"программы", находящиеся во взаимодействии со внешними объектами
2 ключевых аспекта:
- стрелочки идут параллельно в обе стороны
- узлы имеют дополнительный "параметр"

Открытые игры
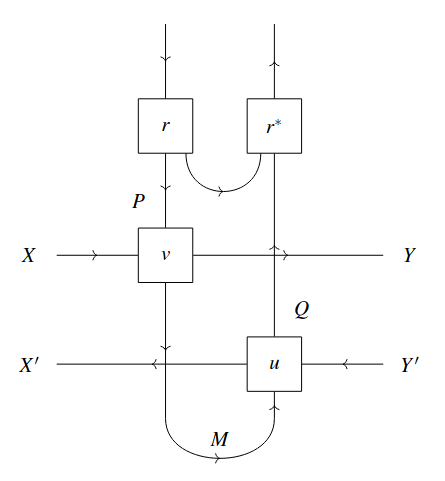
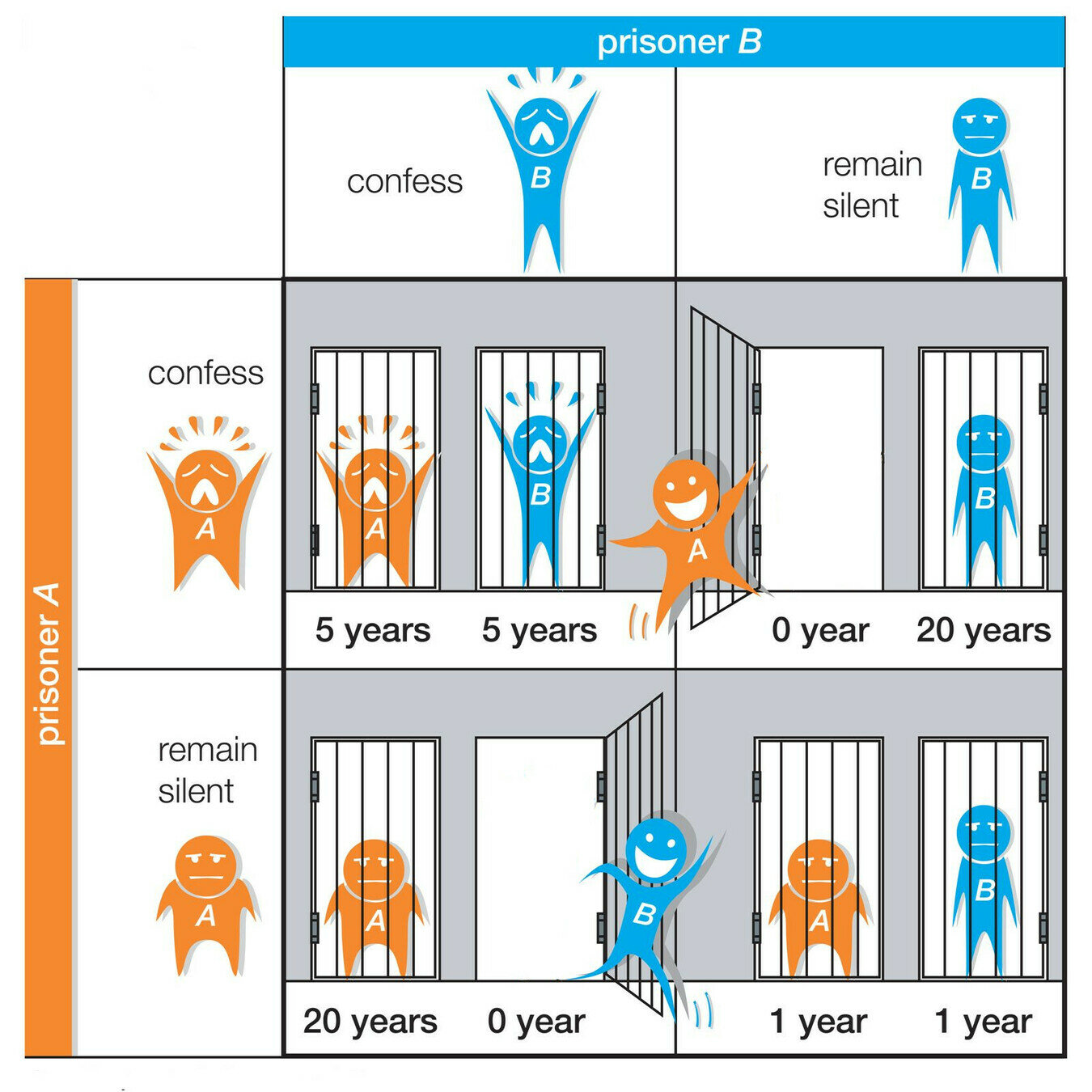
составные игры
максимизация выигрыша
Заключение
Быстрое и медленное мышление

- Статистические методы - быстрые, общие, неточные
- Логические и поисковые методы - медленные, специфичные, надежные
Ссылки
Контакты

Теоремы, которые меняют мир: от компиляторов до экономики
By Alex Gryzlov
Теоремы, которые меняют мир: от компиляторов до экономики
- 105



