REDES NEURONALES CONVOLUCIONALES
Deep Learning - Clase 2
Cristóbal Silva
Si el input es una imágen,
¿cuántos parámetros tiene la primera capa oculta de H neuronas?
Imagen pequeña
80x80x3
19,200 x H

Fotografía 720p
1280x720x3
2,764,800 x H
Alto x Ancho x Nº de Canales (RGB)
¡Solo en la primera capa!
Imágenes como entrada
Reconocimiento de Objetos
Usualmente se requería vasto conocimiento en Visión Computacional
para atacar estos problemas



Bounding-Box
Segmentación
Clasificación de Imágenes
Segmentación Semántica
cat
Detección
Reconocimiento
cat
grass
Reconocimiento de Objetos
Usualmente se requería vasto conocimiento en Visión Computacional
para atacar estos problemas



Bounding-Box
Segmentación
Clasificación de Imágenes
Segmentación Semántica
cat
Detección
Reconocimiento
cat
grass
¡Foco de esta clase!
| 1 | 7 | 7 | 8 | 9 | 4 | 2 | 6 |
| 3 | 8 | 6 | 3 | 4 | 9 | 6 | 0 |
| 4 | 7 | 4 | 7 | 0 | 1 | 1 | 4 |
| 6 | 6 | 2 | 6 | 3 | 6 | 2 | 5 |
| 8 | 5 | 1 | 2 | 2 | 0 | 6 | 3 |
| 0 | 5 | 5 | 4 | 2 | 7 | 9 | 3 |
| 6 | 3 | 9 | 1 | 9 | 6 | 0 | 9 |
| 1 | 4 | 0 | 5 | 2 | 1 | 0 | 1 |
A cualquier imagen podemos aplicarle un operador o transformación cuya salida es una nueva imagen modificada
Conceptos básicos
Convolución
*
filtro o kernel
=
| 3 | 3 | 5 |
| 2 | 1 | 1 |
| 3 | 0 | 4 |
| 1 | 7 | 7 | 8 | 9 | 4 | 2 | 6 |
| 3 | 8 | 6 | 3 | 4 | 9 | 6 | 0 |
| 4 | 7 | 4 | 7 | 0 | 1 | 1 | 4 |
| 6 | 6 | 2 | 6 | 3 | 6 | 2 | 5 |
| 8 | 5 | 1 | 2 | 2 | 0 | 6 | 3 |
| 0 | 5 | 5 | 4 | 2 | 7 | 9 | 3 |
| 6 | 3 | 9 | 1 | 9 | 6 | 0 | 9 |
| 1 | 4 | 0 | 5 | 2 | 1 | 0 | 1 |
A cualquier imagen podemos aplicarle un operador o transformación cuya salida es una nueva imagen modificada
Conceptos básicos
Convolución
| 3 | 3 | 5 |
| 2 | 1 | 1 |
| 3 | 0 | 4 |
*
filtro o kernel
=
\(1\cdot3 + 3\cdot2 + 4\cdot3 + 7\cdot3 + 8\cdot1 + 7\cdot0 + 7\cdot5 + 6\cdot1 + 4\cdot4 = 107\)
107
| 1 | 7 | 7 | 8 | 9 | 4 | 2 | 6 |
| 3 | 8 | 6 | 3 | 4 | 9 | 6 | 0 |
| 4 | 7 | 4 | 7 | 0 | 1 | 1 | 4 |
| 6 | 6 | 2 | 6 | 3 | 6 | 2 | 5 |
| 8 | 5 | 1 | 2 | 2 | 0 | 6 | 3 |
| 0 | 5 | 5 | 4 | 2 | 7 | 9 | 3 |
| 6 | 3 | 9 | 1 | 9 | 6 | 0 | 9 |
| 1 | 4 | 0 | 5 | 2 | 1 | 0 | 1 |
A cualquier imagen podemos aplicarle un operador o transformación cuya salida es una nueva imagen modificada
Conceptos básicos
Convolución
*
filtro o kernel
=
\(7\cdot3 + 8\cdot2 + 7\cdot3 + 7\cdot3 + 6\cdot1 + 4\cdot0 + 8\cdot5 + 3\cdot1 + 7\cdot4 = 156\)
107
156
| 3 | 3 | 5 |
| 2 | 1 | 1 |
| 3 | 0 | 4 |
A cualquier imagen podemos aplicarle un operador o transformación cuya salida es una nueva imagen modificada
Conceptos básicos
Convolución
| 1 | 0 | -1 |
| 1 | 0 | -1 |
| 1 | 0 | -1 |
filtro
horizontal
Podemos construir filtros/kernels que obtengan representaciones específicas de una imagen
Detección de Bordes
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |



filtro
vertical
A cualquier imagen podemos aplicarle un operador o transformación cuya salida es una nueva imagen modificada
Conceptos básicos
Convolución
| 1 | 0 | -1 |
| 1 | 0 | -1 |
| 1 | 0 | -1 |
filtro
horizontal
Podemos construir filtros/kernels que obtengan representaciones específicas de una imagen
Detección de Bordes
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |
filtro
vertical

+

A cualquier imagen podemos aplicarle un operador o transformación cuya salida es una nueva imagen modificada
Conceptos básicos
Convolución
Podemos construir filtros/kernels que obtengan representaciones específicas de una imagen
Detección de Bordes
Si la imagen es \( (n\times n) \) y el filtro es \( (f\times f) \) entonces la imagen resultante es \( (n-f+1\times n-f+1) \)
Tamaño de Salida
Ejemplo
| Tamaño de Entrada | |
| Tamaño de Filtro | |
| Tamaño de Salida |
\( 10-3+1 \times 10-3+1 = 8 \times 8 \)
\( 10\times 10 \)
\( 3\times 3 \)
Conceptos básicos
Padding
Padding es una técnica donde se aumenta artificialmente el tamaño de la imagen para mantener el tamaño de la original después del filtro.
| 1 | 7 | 7 | 8 | 9 |
| 3 | 8 | 6 | 3 | 4 |
| 4 | 7 | 4 | 7 | 0 |
| 6 | 6 | 2 | 6 | 3 |
| 8 | 5 | 1 | 2 | 2 |
Sin Padding
\((p=0\))
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 7 | 7 | 8 | 9 | 0 |
| 0 | 3 | 8 | 6 | 3 | 4 | 0 |
| 0 | 4 | 7 | 4 | 7 | 0 | 0 |
| 0 | 6 | 6 | 2 | 6 | 3 | 0 |
| 0 | 8 | 5 | 1 | 2 | 2 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Padding
(\(p=1\))
relleno: 0
\( (n+2p-f+1\times n+2p-f+1) \)
Tamaño de salida con Padding \(p\)
Conceptos básicos
Stride
Stride es una técnica donde en vez de barrer por todos los pixeles de una imagen, nos saltamos algunos entremedio para evitar redundancia
| 1 | 7 | 7 | 8 | 9 | 4 | 2 | 6 |
| 3 | 8 | 6 | 3 | 4 | 9 | 6 | 0 |
| 4 | 7 | 4 | 7 | 0 | 1 | 1 | 4 |
| 6 | 6 | 2 | 6 | 3 | 6 | 2 | 5 |
| 8 | 5 | 1 | 2 | 2 | 0 | 6 | 3 |
| 0 | 5 | 5 | 4 | 2 | 7 | 9 | 3 |
| 6 | 3 | 9 | 1 | 9 | 6 | 0 | 9 |
| 1 | 4 | 0 | 5 | 2 | 1 | 0 | 1 |
| 3 | 3 | 5 |
| 2 | 1 | 1 |
| 3 | 0 | 4 |
*
filtro o kernel
=
\(1\cdot3 + 3\cdot2 + 4\cdot3 + 7\cdot3 + 8\cdot1 + 7\cdot0 + 7\cdot5 + 6\cdot1 + 4\cdot4 = 107\)
107
\( \lfloor \frac{n-f}{S}+1 \rfloor \times \lfloor \frac{n-f}{S}+1 \rfloor \)
Tamaño de salida con Stride \(S\)
Conceptos básicos
Stride
Stride es una técnica donde en vez de barrer por todos los pixeles de una imagen, nos saltamos algunos entremedio para evitar redundancia
| 1 | 7 | 7 | 8 | 9 | 4 | 2 | 6 |
| 3 | 8 | 6 | 3 | 4 | 9 | 6 | 0 |
| 4 | 7 | 4 | 7 | 0 | 1 | 1 | 4 |
| 6 | 6 | 2 | 6 | 3 | 6 | 2 | 5 |
| 8 | 5 | 1 | 2 | 2 | 0 | 6 | 3 |
| 0 | 5 | 5 | 4 | 2 | 7 | 9 | 3 |
| 6 | 3 | 9 | 1 | 9 | 6 | 0 | 9 |
| 1 | 4 | 0 | 5 | 2 | 1 | 0 | 1 |
| 3 | 3 | 5 |
| 2 | 1 | 1 |
| 3 | 0 | 4 |
*
filtro o kernel
=
\(7\cdot3 + 6\cdot2 + 4\cdot3 + 8\cdot3 + 3\cdot1 + 7\cdot0 + 9\cdot5 + 4\cdot1 + 0\cdot4 = 121\)
107
121
\( \lfloor \frac{n-f}{S}+1 \rfloor \times \lfloor \frac{n-f}{S}+1 \rfloor \)
Tamaño de salida con Stride \(S\)
stride = 1
Conceptos básicos
Convolución en volúmen
Los conceptos anteriores sirven para una imagen 2D,
¿qué ocurre con las imágenes RGB?
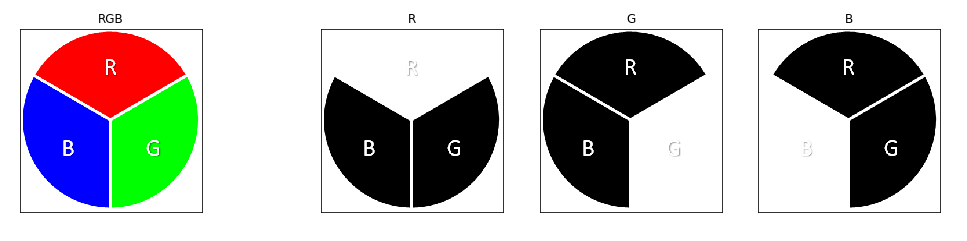
Los filtros en este caso deben tener una dimensión igual al número de canales de la imagen a convolucionar
Entrada:
Filtro:
Salida:
\( n \times n \times c \)
\( f \times f \times c \)
\( n-f+1 \times n-f+1 \)
¡Mismo tamaño!
La salida sigue siendo 2D pues cada pixel de salida es la suma de todo el cubo que general el filtro
Conceptos básicos
Convolución en volúmen
Los conceptos anteriores sirven para una imagen 2D,
¿qué ocurre con las imágenes RGB?
*
\( n \times n \times 3 \)
\( f \times f \times 3 \)
=
\( n-f+1 \times n-f+1 \)
Aprovechar estructura compartida entre pixeles de una imagen para reducir el número de parámetros.
Capa Convolucional
Cada filtro aprendido en el entrenamiento representará una estructura visual característica de los objetos a clasificar (bordes, caras, curvas, etc.)
*
*
Aplicamos K filtros de \( f \times f \times c \)
El valor de cada filtro se aprende con el entrenamiento de la red
Motivación
Capa Convolucional
Cada filtro aprendido en el entrenamiento representará una estructura visual característica de los objetos a clasificar (bordes, caras, curvas, etc.)
ReLU( + bias)
ReLU( + bias)
La salida de la capa convolucional es una función de activación aplicada cada filtro
(e.g. ReLU)
Aprovechar estructura compartida entre pixeles de una imagen para reducir el número de parámetros.
Motivación
Capa Convolucional
Aprovechar estructura compartida entre pixeles de una imagen para reducir el número de parámetros.
Motivación
Sabemos que
- Cada filtro es una convolución en volumen
- La salida de una convolución en volumen es de 2 dimensiones
Tamaño de Salida
Entonces
- Si la capa convolucional tiene \(K\) filtros, la salida de la capa es
donde cada filtro aprenderá sus propios pesos
Capa de Pooling
| 1 | 7 | 7 | 2 |
| 3 | 8 | 6 | 3 |
| 4 | 7 | 4 | 7 |
| 6 | 6 | 2 | 6 |
max-pool
size = 2
stride = 2
| 8 | |
La capa de pooling no aprende ningún parámetro, solamente es una operación sobre matrices.
Reducir dimensionalidad para tener menos parámetros.
A partir de la ventana de pixeles, la salida puede ser:
- Máximo de la ventana de pixeles
- Promedio de la ventana de pixeles
Motivación
También ayuda a la invariancia a traslación, pero puede perder información útil al tratar de generalizar
Capa Fully-Connected
Capa de Pooling
| 1 | 7 | 7 | 2 |
| 3 | 8 | 6 | 3 |
| 4 | 7 | 4 | 7 |
| 6 | 6 | 2 | 6 |
| 8 | 6 |
max-pool
size = 2
stride = 2
La capa de pooling no aprende ningún parámetro, solamente es una operación sobre matrices.
Reducir dimensionalidad para tener menos parámetros.
A partir de la ventana de pixeles, la salida puede ser:
- Máximo de la ventana de pixeles
- Promedio de la ventana de pixeles
Motivación
También ayuda a la invariancia a traslación, pero puede perder información útil al tratar de generalizar
Capa de Pooling
| 1 | 7 | 7 | 2 |
| 3 | 8 | 6 | 3 |
| 4 | 7 | 4 | 7 |
| 6 | 6 | 2 | 6 |
| 8 | 6 |
| 7 |
max-pool
size = 2
stride = 2
La capa de pooling no aprende ningún parámetro, solamente es una operación sobre matrices.
Reducir dimensionalidad para tener menos parámetros.
A partir de la ventana de pixeles, la salida puede ser:
- Máximo de la ventana de pixeles
- Promedio de la ventana de pixeles
Motivación
También ayuda a la invariancia a traslación, pero puede perder información útil al tratar de generalizar
Capa de Pooling
| 1 | 7 | 7 | 2 |
| 3 | 8 | 6 | 3 |
| 4 | 7 | 4 | 7 |
| 6 | 6 | 2 | 6 |
| 8 | 6 |
| 7 | 7 |
max-pool
size = 2
stride = 2
La capa de pooling no aprende ningún parámetro, solamente es una operación sobre matrices.
Reducir dimensionalidad para tener menos parámetros.
A partir de la ventana de pixeles, la salida puede ser:
- Máximo de la ventana de pixeles
- Promedio de la ventana de pixeles
Motivación
También ayuda a la invariancia a traslación, pero puede perder información útil al tratar de generalizar
Capa de Pooling
reverse
max-pool
size = 2
stride = 2
| 8 | 8 | 6 | 6 |
| 8 | 8 | 6 | 6 |
| 7 | 7 | 7 | 7 |
| 7 | 7 | 7 | 7 |
| 8 | 6 |
| 7 | 7 |
El upsample es opcional, y se usa en arquitecturas donde se espera que la salida tenga un tamaño igual a la entrada (arquitecturas encoder-decoder)
Reducir dimensionalidad para tener menos parámetros.
A partir de la ventana de pixeles, la salida puede ser:
- Máximo de la ventana de pixeles
- Promedio de la ventana de pixeles
Motivación
La operación inversa al pooling es expandir la imagen (upsample) replicando valores para volver al tamaño original
Ejemplo: Esquema de CNN

conv1
\( n\times n\times 1 \)
\( n\times n\times 3 \)
\( \frac{n}{2}\times \frac{n}{2}\times 3 \)
input
pool1
conv2
\( \frac{n}{2}\times \frac{n}{2}\times 5 \)
Por simplicidad se asume que todas las convoluciones tienen padding.
fc1
out
\( M\times 1 \)
0
0
0
0
0
0
0
0
1
0
\( 10 \)
Input: Imágen de tamaño \( n\times n \)
Salida: Vector one-hot de tamaño 10
La capa fc1 es una capa “Fully-Connected”, donde los filtros de conv2 se concatenan para formar un vector que se usa para mapear a las M neuronas de esta capa.
(3 filtros \(f_1\times f_1\))
(5 filtros \(f_2\times f_2\))
(\(2\times 2\) con stride 2)
(\(M\) neuronas)
Entre fc1 y out funciona igual que un perceptrón multi-capa.
Ejemplo: Parámetros de CNN
Veamos cuántos parámetros tiene una red convolucional con las siguientes características
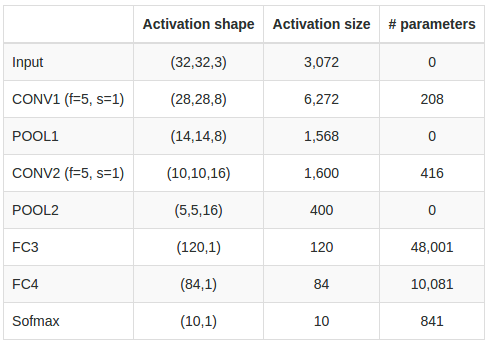
608
3216
48,120
10,164
850

8 filtros de 5x5x3 + bias
\( \Rightarrow (5\cdot 5\cdot 3 + 1) \cdot 8 \) \( = 608 \)
16 filtros de 5x5 + bias \( \Rightarrow \left(5\cdot 5\cdot 8 + 1\right)\cdot 16 \) \(= 3216 \)
400 entradas + 120 salidas + 120 bias
\(\Rightarrow 400\cdot 120 + 120\) \(=48,120\)
Ejemplo: Parámetros de CNN
Veamos cuántos parámetros tiene una red convolucional con las siguientes características
608
3216
48,120
10,164
850
Inspiración biológica
- El video muestra un animal con un electrodo conectado el cuál solo recibe estímulo ante patrones visuales simples (en este caso, una línea en diagonal).
- Esto da indicios de hay regiones del cerebro encargadas de procesar patrones simples que al combinarse permiten entender estructuras más complejas.
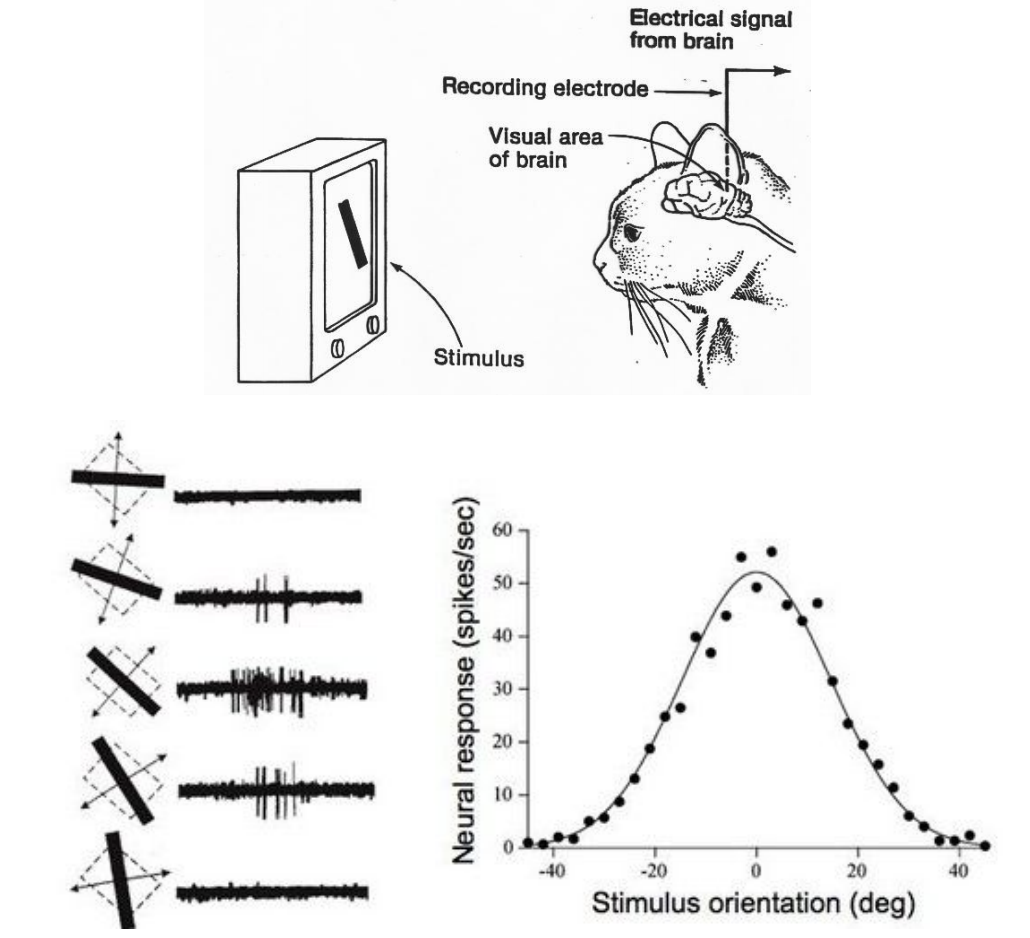
Convolutional Neural Networks for Visual Recognition,
Lecture 7, Stanford CS231n (2016)
Visualizar el Aprendizaje
Existen varias metodologías para entender qué aprenden las CNNs.
Algunas técnicas destacadas ordenadas por dificultad de implementar:
- Visualizar los filtros aprendidos
- Visualizar activaciones de ejemplos individuales
- Visualizar ejemplos que maximizan la activación de neuronas
- Métodos basados en optimización (e.g. ascenso de gradiente)

Filtros aprendidos en la primera capa de la red AlexNet
Convolutional Neural Networks for Visual Recognition,
Lecture 7, Stanford CS231n (2016)
Visualizar el Aprendizaje
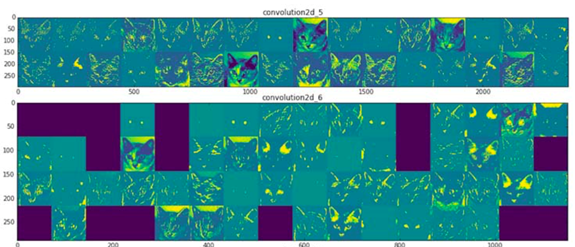
Activación de primeras dos capas para la foto de un gato en una red entrenada con imágenes de perros y gatos
Existen varias metodologías para entender qué aprenden las CNNs.
Algunas técnicas destacadas ordenadas por dificultad de implementar:
- Visualizar los filtros aprendidos
- Visualizar activaciones de ejemplos individuales
- Visualizar ejemplos que maximizan la activación de neuronas
- Métodos basados en optimización (e.g. ascenso de gradiente)
Deep Learning with Python,
Francois Chollet, 1st edition, 2017
Visualizar el Aprendizaje
Existen varias metodologías para entender qué aprenden las CNNs.
Algunas técnicas destacadas ordenadas por dificultad de implementar:
- Visualizar los filtros aprendidos
- Visualizar activaciones de ejemplos individuales
- Visualizar ejemplos que maximizan la activación de neuronas
- Métodos basados en optimización (e.g. ascenso de gradiente)

Ejemplos que maximizan activación de algunas neuronas de la primera capa de una red convolucional.
Son 9 ejemplos por neurona. Notar como se maximizan ante orientaciones particulares.
Convolutional Neural Networks,
Andrew Ng, Coursera, 2017
Visualizar el Aprendizaje
Existen varias metodologías para entender qué aprenden las CNNs.
Algunas técnicas destacadas ordenadas por dificultad de implementar:
- Visualizar los filtros aprendidos
- Visualizar activaciones de ejemplos individuales
- Visualizar ejemplos que maximizan la activación de neuronas
- Métodos basados en optimización (e.g. ascenso de gradiente)
Ejemplos que maximizan activación de algunas neuronas de la primera capa de una red convolucional.
Son 9 ejemplos por neurona. Notar como se maximizan ante orientaciones particulares.
Convolutional Neural Networks,
Andrew Ng, Coursera, 2017

Visualizar el Aprendizaje
Existen varias metodologías para entender qué aprenden las CNNs.
Algunas técnicas destacadas ordenadas por dificultad de implementar:
- Visualizar los filtros aprendidos
- Visualizar activaciones de ejemplos individuales
- Visualizar ejemplos que maximizan la activación de neuronas
- Métodos basados en optimización (e.g. ascenso de gradiente)
Feature Visualization,
Chris Olah et. al., distill.pub, 2017

Representación de features locales y globales en función de objetivo de optimización
Referencias
Visualización
- Zeiler et. al., Visualizing and Understanding Convolutional Networks,
European Conference on Computer Vision (ECCV), 2014 - Olah et. al., Feature Visualization,
distill.pub, 2017
Arquitecturas
-
LeNet
- LeCun et. al., Gradient-based Learning Applied to Document Recognition,
Proceedings of IEEE, 1998
- LeCun et. al., Gradient-based Learning Applied to Document Recognition,
-
AlexNet
- Krizhevsky et. al., ImageNet Classification with Deep Convolutional Neural Networks,
Neural Information Processing Systems (NIPS), 2012
- Krizhevsky et. al., ImageNet Classification with Deep Convolutional Neural Networks,
-
ResNet
- He et. al., Deep Residual Learning for Image Recognition,
Computer Vision and Pattern Recognition (CVPR), 2016
- He et. al., Deep Residual Learning for Image Recognition,
-
InceptionNet
- Szegedy et. al., Going deeper with convolutions,
Computer Vision and Pattern Recognition (CVPR), 2015
- Szegedy et. al., Going deeper with convolutions,
-
VGG
- Liu et. al., Very deep convolutional neural network based image classification using small training sample size, Asian Conference on Pattern Recognition (ACPR), 2015
Referencias
Otras referencias
-
Deep Learning Book,
Goodfellow I., Bengio Y., Courville A.,
MIT Press, 2016 -
Deep Learning Specialization,
Deeplearning.ai, - Introduction to Deep Learning,
MIT 6.S191, 2017
Redes Neuronales Convolucionales
-
Convolutional Neural Networks for Visual Recognition,
Stanford CS231, 2016-2018
2 - Redes Neuronales Convolucionales
By crsilva
2 - Redes Neuronales Convolucionales
- 902



