REDES RECURRENTES
Deep Learning - Clase 3
Cristóbal Silva
Secuencias como entrada
¿Qué pueden ser datos secuenciales?
Señales
Audio, financieras, médicas, etc.
The only thing necessary for the triumph of evil is for good men to do nothing.
Edmund Burke
Texto
Palabras, caracteres, n-gramas, etc.

Imágenes
Videos (secuencia de frames)
Secuencias como entrada
¿Qué problemas pueden resolver?

Entrada y salida pueden ser secuencias; a veces del mismo tamaño, a veces de diferente tamaño.
A veces solo la entrada es una secuencia; a veces solo la salida es una secuencia.
Secuencias como entrada
Distintas arquitecturas, dependiendo del tamaño de la entrada y la salida
Each rectangle is a vector and arrows represent functions (e.g. matrix multiply). Input vectors are in red, output vectors are in blue and green vectors hold the RNN's state (more on this soon). From left to right: (1) Vanilla mode of processing without RNN, from fixed-sized input to fixed-sized output (e.g. image classification). (2) Sequence output (e.g. image captioning takes an image and outputs a sentence of words). (3) Sequence input (e.g. sentiment analysis where a given sentence is classified as expressing positive or negative sentiment). (4) Sequence input and sequence output (e.g. Machine Translation: an RNN reads a sentence in English and then outputs a sentence in French). (5) Synced sequence input and output (e.g. video classification where we wish to label each frame of the video). Notice that in every case are no pre-specified constraints on the lengths sequences because the recurrent transformation (green) is fixed and can be applied as many times as we like.
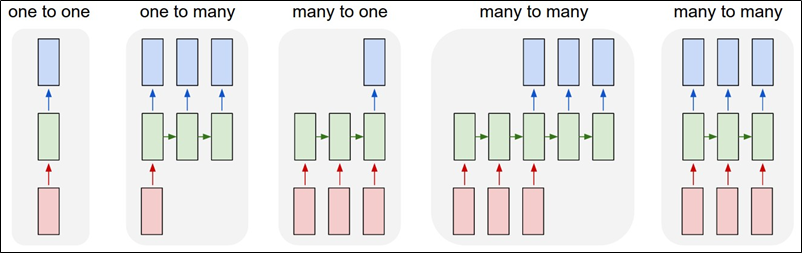
The Unreasonable Effectiveness of Recurrent Neural Networks,
Andrej Karpathy, 2015
Forward-Pass
Notación compacta
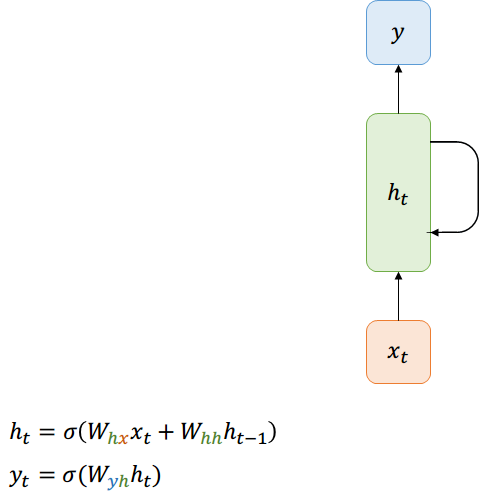
Forward-Pass

Many-to-Many
Forward-Pass
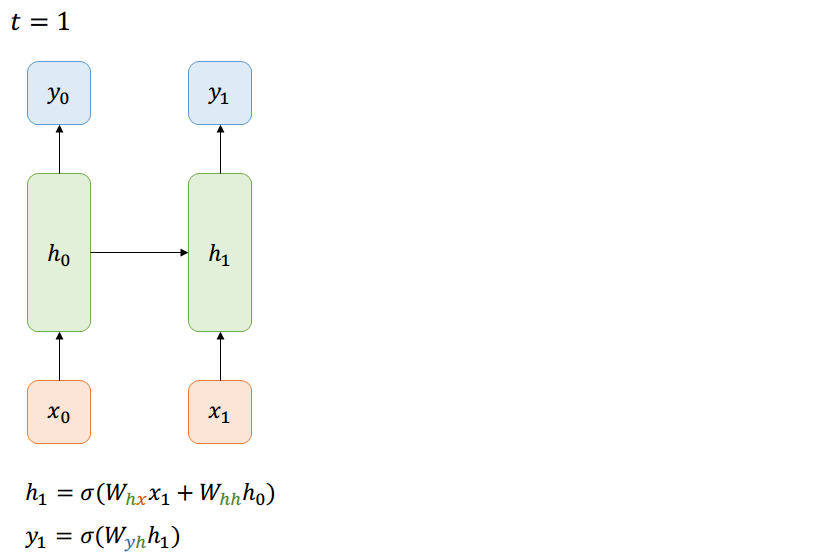
Many-to-Many
Forward-Pass
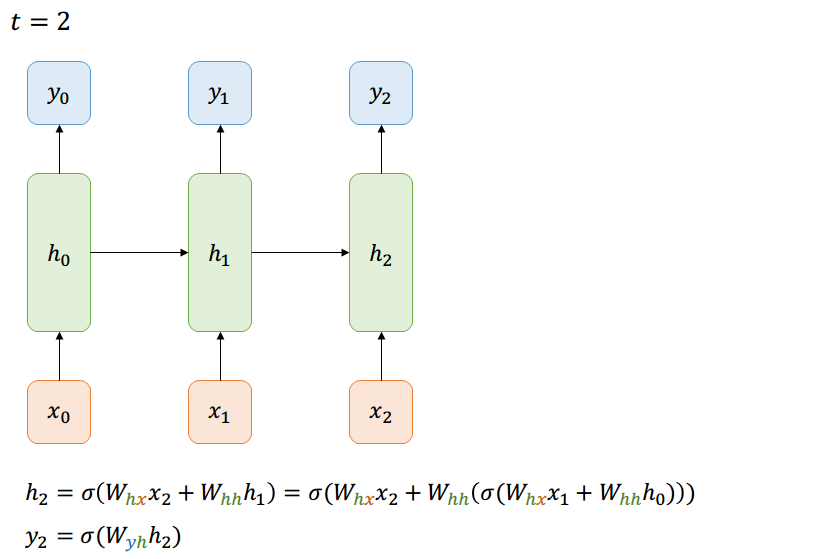
Many-to-Many
Forward-Pass
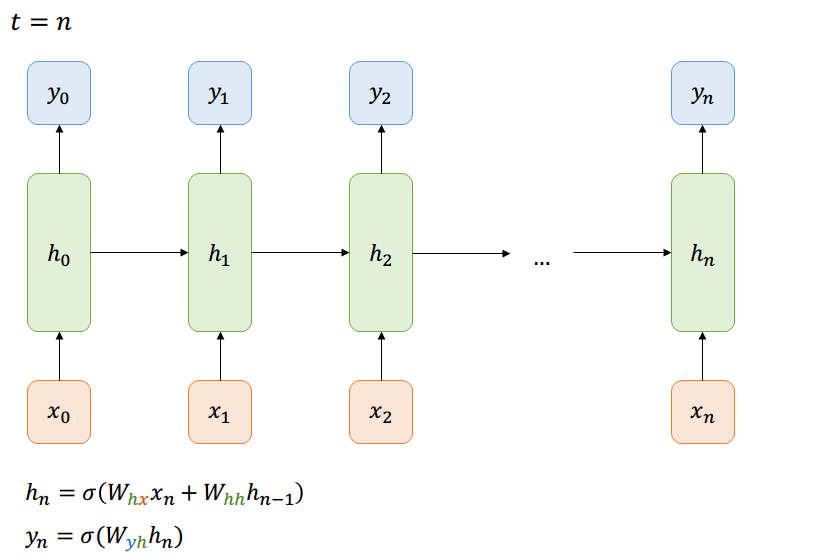
Many-to-Many
Forward-Pass
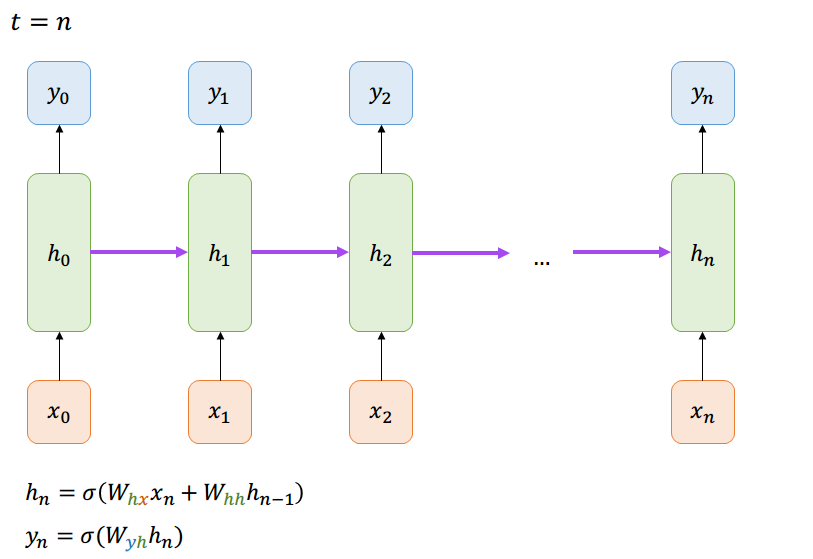
Las dependencias se acumulan,
la red no es solo deep ahora, si no que también es wide
Many-to-Many
Función de Costo
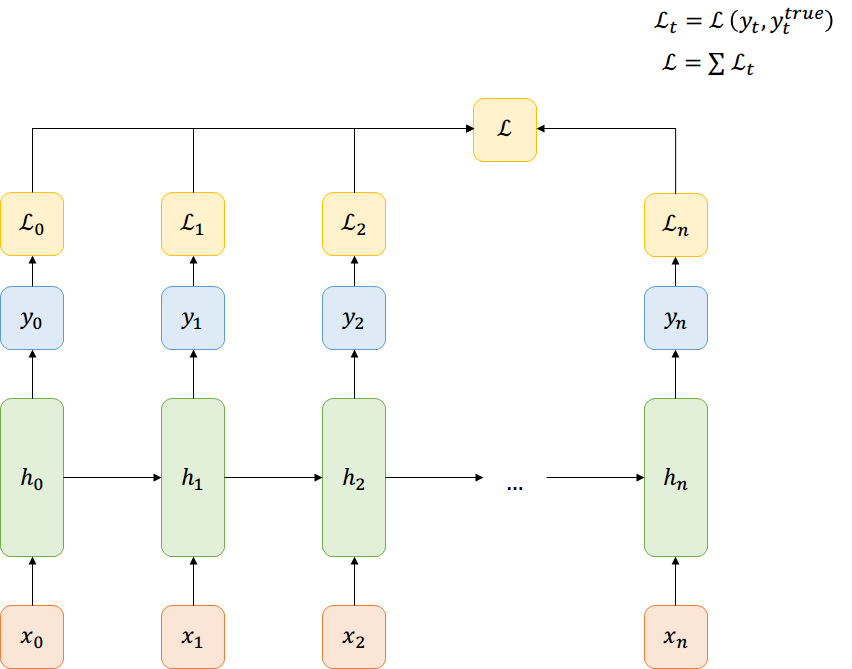
Many-to-Many
Back-prop through time
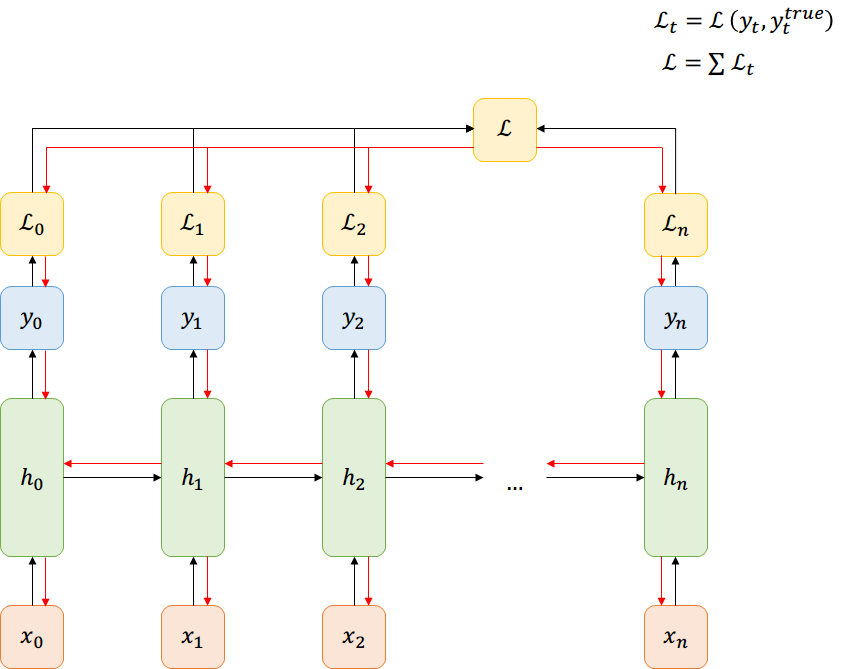
Many-to-Many
Forward-Pass
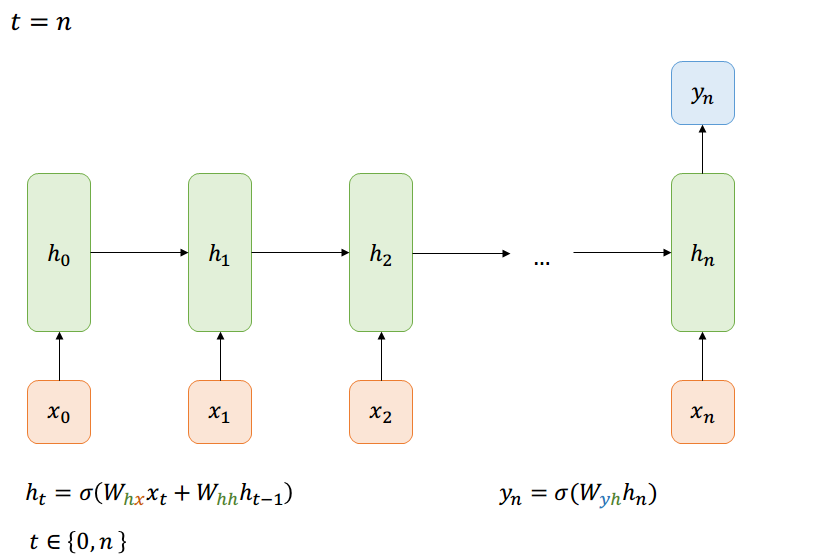
Many-to-One
Forward-Pass
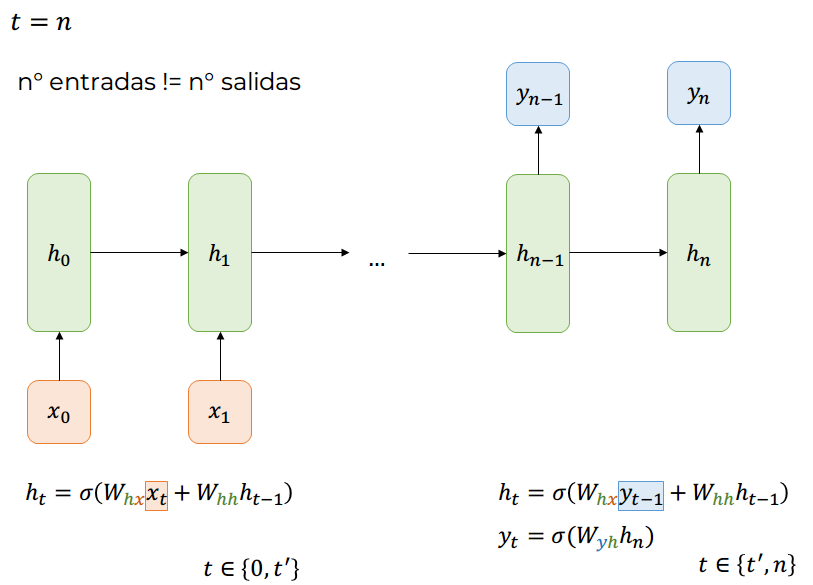
Many-to-Many
Forward-Pass
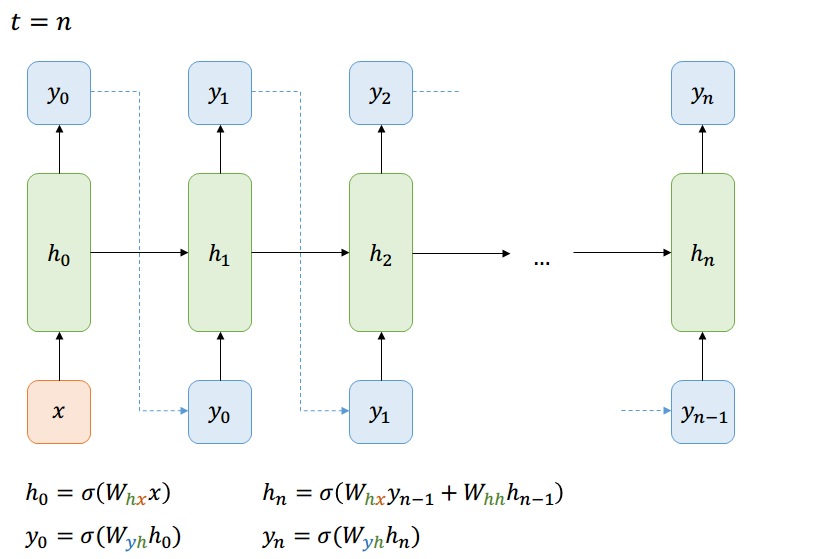
One-to-Many
Ejemplo - Modelar Lenguaje
One-to-Many
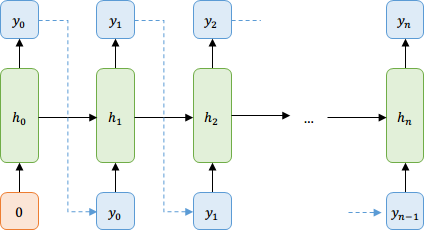
Supongamos que queremos predecir la probabilidad de ver una secuencia de letras. Sabemos que
¿Cómo transmitimos eso a la red?
\( y_t \) es un vector con la probabilidad de cada letra dada la anterior
Ejemplo - Modelar Lenguaje
One-to-Many
Supongamos que queremos predecir la probabilidad de ver una secuencia de letras. Sabemos que
¿Cómo transmitimos eso a la red?
\( y_t \) es un vector con la probabilidad de cada letra dada la anterior
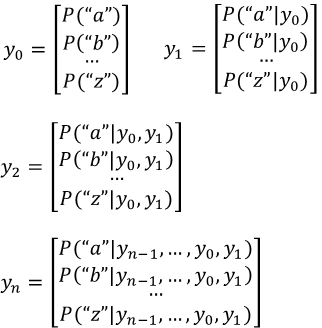

Ejemplo - Modelar Lenguaje
One-to-Many
Supongamos que queremos predecir la probabilidad de ver una secuencia de letras. Sabemos que
¿Cómo transmitimos eso a la red?
\( y_t \) es un vector con la probabilidad de cada letra dada la anterior
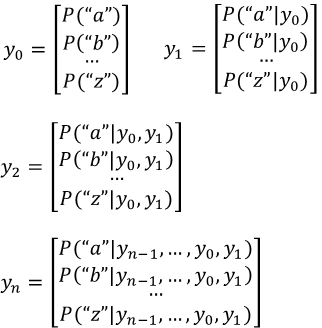

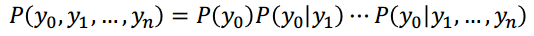
Regla de la cadena de probabilidades
Ejemplo - Modelar Lenguaje
One-to-Many
Supongamos que queremos predecir la probabilidad de ver una secuencia de letras. Sabemos que
¿Cómo transmitimos eso a la red?
\( y_t \) es un vector con la probabilidad de cada letra dada la anterior
Obtener muestras del modelo
Para \( \ t = 1:N \)
- Sacar vector de probabilidades a partir de la entrada
- Muestrear un caracter usando esas probabilidades
- Usar el caracter obtenido como siguiente entrada
Los modelos de lenguaje no son solamente a base de caracteres, también pueden construirse usando palabras completas a partir de un diccionario de palabras.
Vanishing/Exploding Gradients
Volviendo al primer ejemplo, ¿qué pasa con las dependencias en el tiempo?
¿cómo influye la primera "capa" sobre la "última"?
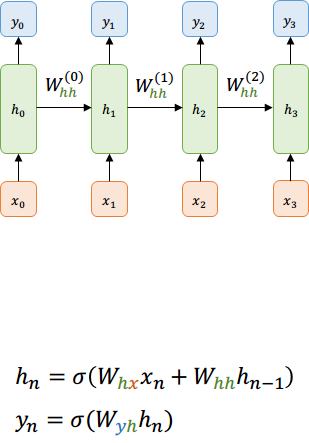
Volviendo al primer ejemplo, ¿qué pasa con las dependencias en el tiempo?
¿cómo influye la primera "capa" sobre la "última"?

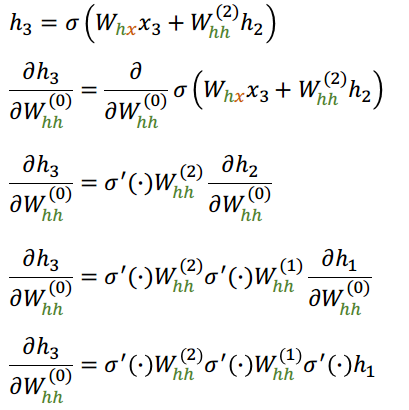
Vanishing/Exploding Gradients
Volviendo al primer ejemplo, ¿qué pasa con las dependencias en el tiempo?
¿cómo influye la primera "capa" sobre la "última"?

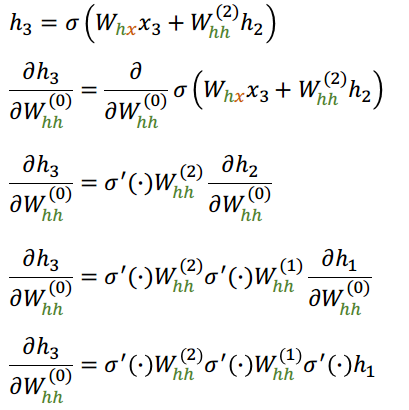
¿Qué pasa si tenemos 100 en vez de 3 salidas?
Vanishing/Exploding Gradients
A medida que volvemos en el tiempo, la influencia depende de una mayor cantidad de multiplicaciones de matrices \( W_{hh} \)
Vanishing/Exploding Gradients
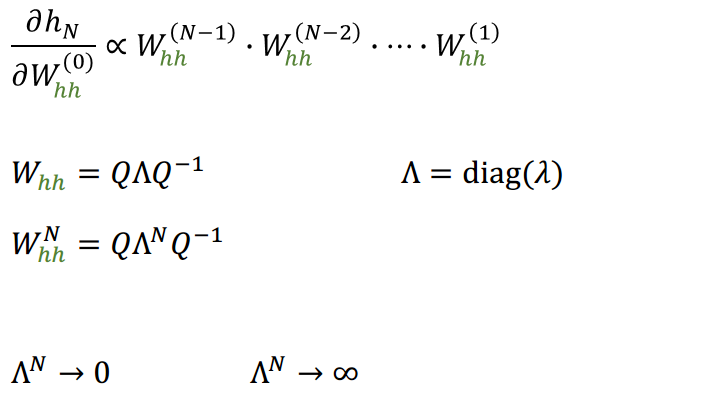
Si los valores propios de la matriz no son cercanos a 1
Matriz de valores propios
A medida que volvemos en el tiempo, la influencia depende de una mayor cantidad de multiplicaciones de matrices \( W_{hh} \)
Vanishing/Exploding Gradients
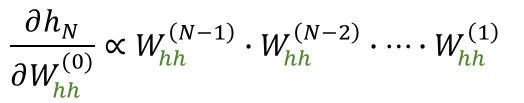
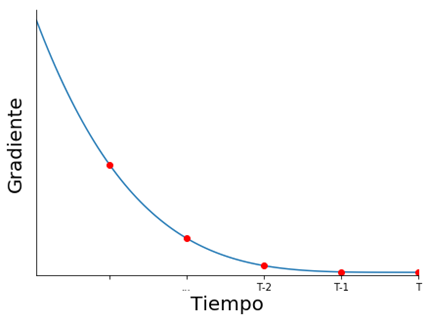
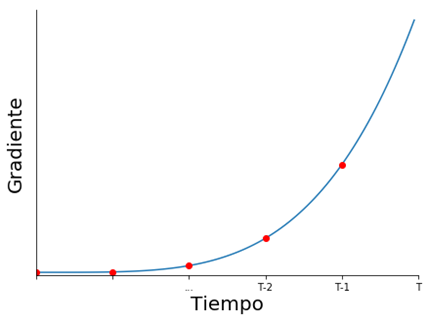
A medida que volvemos en el tiempo, la influencia depende de una mayor cantidad de multiplicaciones de matrices \( W_{hh} \)
Vanishing/Exploding Gradients
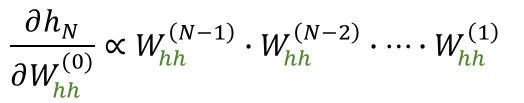
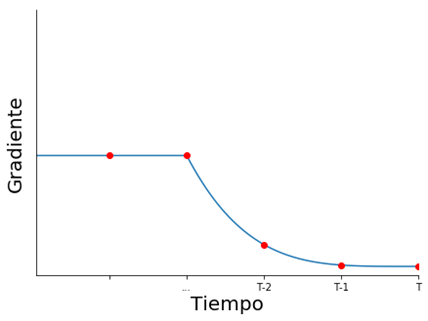
Exploding Gradient puede mitigarse poniendo una cota superior al gradiente
Vanishing Gradient requiere una solución más compleja
Una capa oculta es simplemente una fully-connected con entrada y salida únicas.
Usualmente la función de activación será \( \tanh \) .
La entrada puede ser \( x_t \) o \( h_t \) pero por simplicidad usaremos solo la primera.
Capa oculta actual

Long-Short-Term-Memory (LSTM)
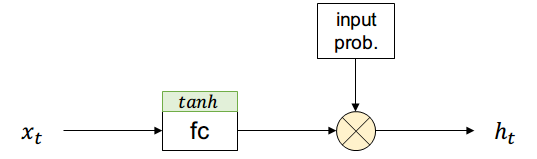
Supongamos que existe una compuerta que permite controlar si una activación pasa o no con cierta probabilidad (short-term memory)
Long-Short-Term-Memory (LSTM)
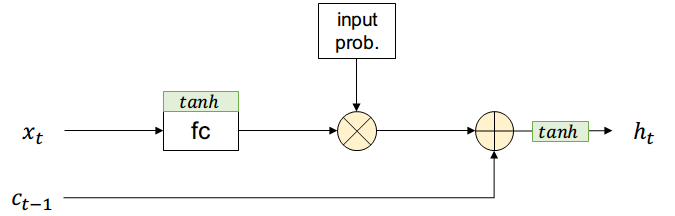
Adicionalmente existirá una entrada \( c_{t-1} \) que contiene información de todos los estados anteriores (long-term memory) y no pasa por el filtro de input
Supongamos que existe una compuerta que permite controlar si una activación pasa o no con cierta probabilidad (short-term memory)
La salida es una combinación entre short-term y long-term más una función de activación
Long-Short-Term-Memory (LSTM)
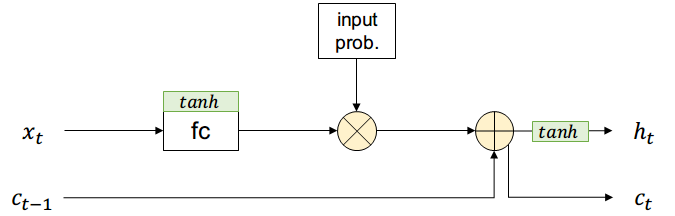
Adicionalmente existirá una entrada \( c_{t-1} \) que contiene información de todos los estados anteriores (long-term memory) y no pasa por el filtro de input
Supongamos que existe una compuerta que permite controlar si una activación pasa o no con cierta probabilidad (short-term memory)
La salida es una combinación entre short-term y long-term más una función de activación
La nueva long-term memory es pasada al estado siguiente sin aplicar activación no-lineal
Long-Short-Term-Memory (LSTM)
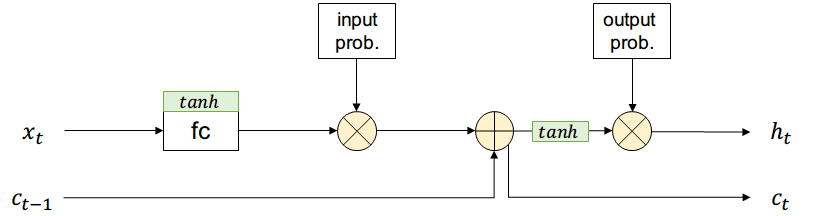
La salida pasará por una compuerta similar a la de entrada, controlando las partes de la long-term memory que formarán parte de la salida que usará el estado siguiente \( h_{t+1} \) y la salida actual \( y_t \)
Adicionalmente existirá una entrada \( c_{t-1} \) que contiene información de todos los estados anteriores (long-term memory) y no pasa por el filtro de input
Supongamos que existe una compuerta que permite controlar si una activación pasa o no con cierta probabilidad (short-term memory)
La salida es una combinación entre short-term y long-term más una función de activación
La nueva long-term memory es pasada al estado siguiente sin aplicar activación no-lineal
Long-Short-Term-Memory (LSTM)
La salida pasará por una compuerta similar a la de entrada, controlando las partes de la long-term memory que formarán parte de la salida que usará el estado siguiente \( h_{t+1} \) y la salida actual \( y_t \)
Adicionalmente existirá una entrada \( c_{t-1} \) que contiene información de todos los estados anteriores (long-term memory) y no pasa por el filtro de input
Supongamos que existe una compuerta que permite controlar si una activación pasa o no con cierta probabilidad (short-term memory)
La salida es una combinación entre short-term y long-term más una función de activación
La nueva long-term memory es pasada al estado siguiente sin aplicar activación no-lineal
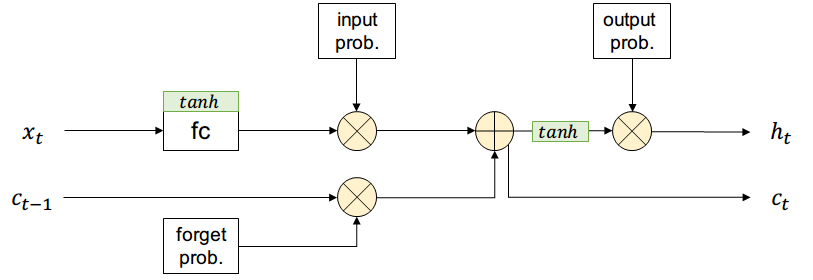
Finalmente se añade la compuerta de olvido, que borrará partes de long-term memory según sea necesario para la red
Long-Short-Term-Memory (LSTM)
Reordenando todo lo anterior tenemos el siguiente esquema de LSTM.
¿De dónde salen las probabilidades de cada compuerta?
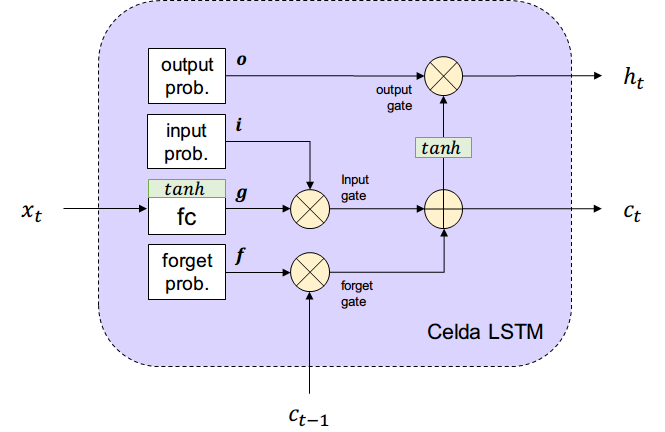
Long-Short-Term-Memory (LSTM)
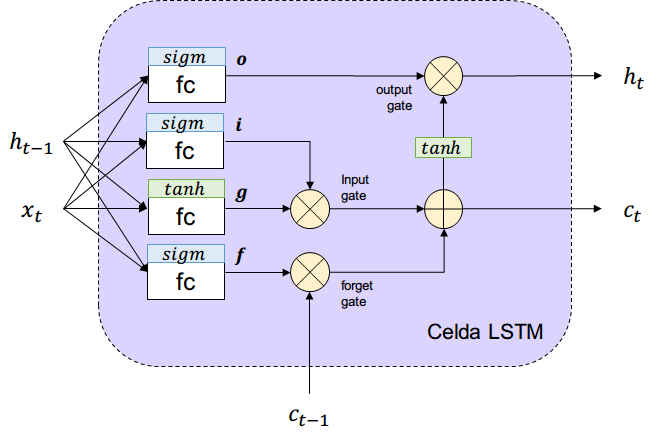
Reordenando todo lo anterior tenemos el siguiente esquema de LSTM.
¿De dónde salen las probabilidades de cada compuerta?
Se aprenden a partir de la entrada
Long Short Term Memory,
Hochreiter S., Schmidhuber J., Neural Computation, 1997
Long-Short-Term-Memory (LSTM)

Reordenando todo lo anterior tenemos el siguiente esquema de LSTM.
¿De dónde salen las probabilidades de cada compuerta?
Se aprenden a partir de la entrada
Long Short Term Memory,
Hochreiter S., Schmidhuber J., Neural Computation, 1997
Long-Short-Term-Memory (LSTM)
La nueva celda reemplaza todas las neuronas de la capa oculta
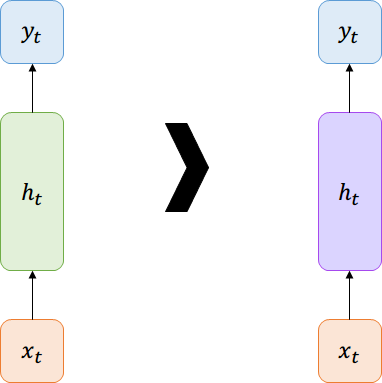
Gated-Recurrent-Unit (GRU)
Más simple que LSTM en cantidad de parámetros y activaciones
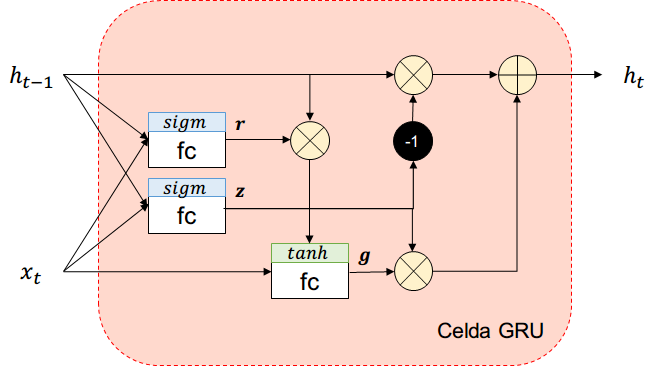
Diferencias con LSTM
Ya no existe long-term memory \( c_t \)
Una compuerta controla el input y el forget.
Si la salida de la compuerta es 1
- input se abre, forget se cierra
Si la salida de la compuerta es 0
- forget se abre, input se cierra
Ya no existe compuerta output
Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation,
Cho K. et. al., Conference on Empirical Methods in Natural Language Processing, 2014
Gated-Recurrent-Unit (GRU)
Más simple que LSTM en cantidad de parámetros y activaciones

Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation,
Cho K. et. al., Conference on Empirical Methods in Natural Language Processing, 2014
Redes Neuronales Recurrentes
- Chapter 14: Recurrent Neural Networks,
Hands-on Machine Learning with Scikit-Learn and TensorFlow, 1st ed., 2017
Celdas
-
LSTM
- Hochreiter et. al., Long Short Term Memory,
Neural Computation, 1997
- Hochreiter et. al., Long Short Term Memory,
-
GRU
- Cho et. al., Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation, Conference on Empirical Methods in Natural Language Processing, 2014
- Week 1: Recurrent Neural Networks,
Sequence Models, deeplearning.ai, 2018
-
Deep Learning II: Redes Recurrentes,
Charla GAMES, Universidad de Chile, 2016
Referencias
Otras referencias
-
Deep Learning Book,
Goodfellow I., Bengio Y., Courville A.,
MIT Press, 2016 -
Deep Learning Specialization,
Deeplearning.ai, - Introduction to Deep Learning,
MIT 6.S191, 2017
Redes Neuronales Convolucionales
-
Convolutional Neural Networks for Visual Recognition,
Stanford CS231, 2016-2018
Referencias
3 - Redes Recurrentes
By crsilva
3 - Redes Recurrentes
- 714



