INTRODUCCION A DEEP LEARNING
Deep Learning - Clase 1
Cristóbal Silva
¿Qué es Deep Learning?
Inteligencia Artificial
Machine Learning
Deep Learning
Agentes que aprenden a imitar "comportamiento inteligente"
Algoritmos que aprenden a partir de datos
Aprendizaje basado en Redes Neuronales con grandes cantidades de datos
1998 - LeNet 5
2012 - AlexNet
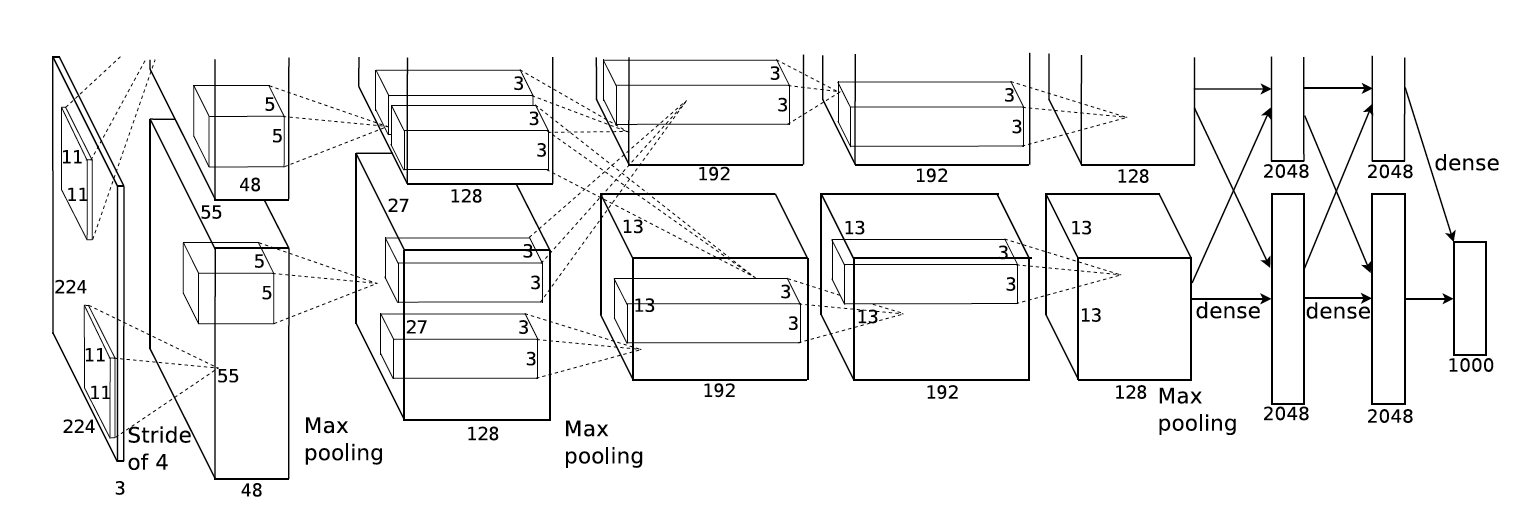
Contexto histórico
¿Qué han logrado desde entonces?
Detección de objetos en ambientes no controlados
Mask R-CNN (Facebook)
¿Qué han logrado desde entonces?
Modelos para generar voz
Mejor resultado antes de Deep Learning
WaveNet (Google Deepmind)
¿Qué han logrado desde entonces?
Transferencia de estilo
Deep Image Analogy (Microsoft)
¿Cómo lo logra?
No necesitamos diseñar features
Capa 1
Capa 2
Capa 3
bordes, esquinas
ojos, narices, bocas
partes de rostros
¿Cómo lo logra?
Tenemos más recursos que antes
Datos
Hardware
Frameworks
La mayoría respaldados por grandes compañías
Frameworks
Se basan en la idea del grafo computacional
f(a, b) = (a + b) \cdot 3b
a
b
u=a+b
v=3*b
f=u*v
Podemos calcular cualquier operación, e.g., el forward-pass de una red neuronal
¿cómo calculamos del backward-pass?
Frameworks
Se basan en la idea del grafo computacional
f(a, b) = (a + b) \cdot 3b
a
b
u=a+b
v=3*b
f=u*v
\frac{\partial f}{\partial a} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial a}
\frac{\partial f}{\partial b} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial b} + \frac{\partial f}{\partial v} \cdot \frac{\partial v}{\partial b}
Se descompone cada derivada usando la regla de la cadena
Frameworks
Se basan en la idea del grafo computacional
\frac{\partial f}{\partial a} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial a}
a
b
u=a+b
v=3*b
f=u*v
\frac{\partial f}{\partial b} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial b} + \frac{\partial f}{\partial v} \cdot \frac{\partial v}{\partial b}
Se descompone cada derivada usando la regla de la cadena
Frameworks
Se basan en la idea del grafo computacional
f(a, b) = (a + b) \cdot 3b
a
b
u=a+b
v=3*b
f=u*v
\frac{\partial (x + y)}{x} = 1
\frac{\partial (x \cdot y)}{x} = y
Se calcula como la magnitud del cambio desde un nodo hacia otro
Frameworks
Se basan en la idea del grafo computacional
\frac{\partial f}{\partial a} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial a}
a
b
u=a+b
v=3*b
f=u*v
\frac{\partial f}{\partial u} = v
\frac{\partial f}{\partial b} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial b} + \frac{\partial f}{\partial v} \cdot \frac{\partial v}{\partial b}
Se calcula como la magnitud del cambio desde un nodo hacia otro
\frac{\partial f}{\partial v} = u
\frac{\partial u}{\partial a} = \frac{\partial u}{\partial b} = 1
\frac{\partial v}{\partial b} = 3
Frameworks
Se basan en la idea del grafo computacional
5
3
u=5+3
v=3*3
f=8*9
\frac{\partial f}{\partial u} = \frac{f(8 + 0.001, 9) - f(8, 9)}{0.001} = 9
\frac{\partial f}{\partial b} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial b} + \frac{\partial f}{\partial v} \cdot \frac{\partial v}{\partial b}
\frac{\partial f}{\partial a} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial a}
\frac{\partial f(u, v)}{\partial u} = \frac{f(u + \varepsilon, v) - f(u, v)}{\varepsilon}
Frameworks
Se basan en la idea del grafo computacional
5
3
u=5+3
v=3*3
f=8*9
\frac{\partial f}{\partial b} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial b} + \frac{\partial f}{\partial v} \cdot \frac{\partial v}{\partial b} = 9 \cdot 1 + 8 \cdot 3 = 33
\frac{\partial f}{\partial a} = \frac{\partial f}{\partial u} \cdot \frac{\partial u}{\partial a} = 9 \cdot 1 = 9
Propuesta: formular regresión logística en grafo
Frameworks
\hat{y}(x) = g(w^{\textrm{T}}x) = \frac{1}{1 + e^{-w^\textrm{T}x}}
J(w) = \frac{1}{N} \sum_{i=1}^{N} \left[ y_i\log(\hat{y}_i) + (1 - y_i)\log(1 - \hat{y}_i) \right]
Regresor
Función de Costo
Frameworks
Se basan en la idea del grafo computacional
Varias formas de calcular una derivada
Diferenciación Numérica
Diferenciación Automática
Diferenciación Simbólica
Aproximación vía diferencias finitas
Se define la derivada de cada operación
Similar a la diferenciación simbólica, pero esta explota la estructura del grafo para evitar cálculos redundates
Hoy en día la mayoría de los frameworks usa diferenciación automática
Variantes o mejoras sobre el Descenso de Gradiente
Algoritmos de Optimización
Momentum
Adagrad
Adadelta
RMSProp
Adam
Agrega un término de "aceleración" al Descenso de Gradiente estocástico
Tasa de aprendizaje adaptiva, distinta para cada parámetro
Tasa de aprendizaje adaptiva, distinta para cada parámetro, extensión de Adagrad
Tasa de aprendizaje adaptiva, distinta para cada parámetro, más un término similar al de Momentum
Tasa de aprendizaje adaptiva, distinta para cada parámetro, extensión de Adagrad
Cada una tiene sus ventajas y sus propios hiper-parámetros
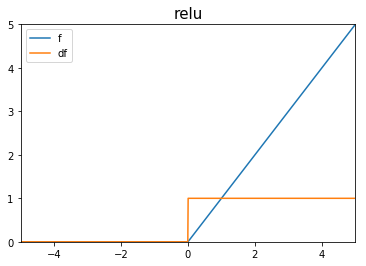
- Función no-lineal recomendada para capas ocultas [1].
- Derivada amigable con descenso de gradiente a pesar de no ser diferenciable en 0.
- "Construir cosas complejas a partir de cosas simples".
f(x) = \max (0, x)
Rectified Linear Unit (ReLU)
Glorot et. al.; Deep Sparse Rectifier Neural Networks; Machine Learning Research; 2011
Funciones de Activación
f(x) = \max (0.01x, x)
Leaky ReLU
Funciones de Activación
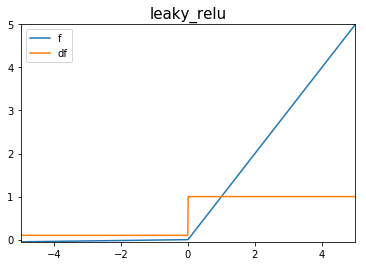
Sirven como alternativas
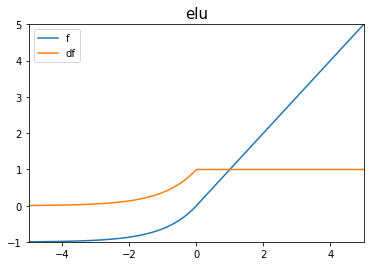
ELU (Exponential Linear Unit)
f(x) = \left\{\begin{matrix}
x & x\geq0\\
a(e^x - 1) & x<0
\end{matrix}\right.
\((a = 1)\)
Funciones de Activación
\sigma(z) = \frac{1}{1 + e^{-z}}
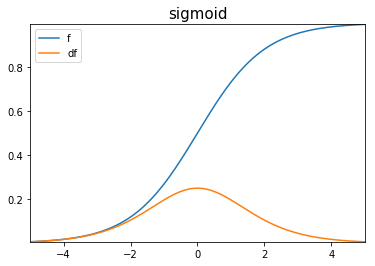
- No recomendada para capas intermedias.
- Ideal para clasificación binaria.
Sigmoidea
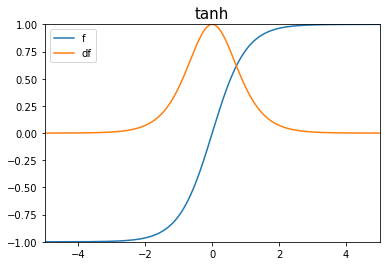
Tangente Hiperbólica
Funciones de Activación
f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}
- No recomendada para capas intermedias.
- Simétrica en 0, a diferencia de la función sigmoidea
- Antes de que se usaran ReLU, esta función era una buena alternativa para capas ocultas ya que su gradiente se comportaba mejor que la sigmoide en esos casos
Deep Learning Bayesiano
Podemos ver la red neuronal como un modelo probabilístico paramétrico
P(\mathbf{y}|\mathbf{x}; \theta)
Optimizar usando Máxima Verosimilitud
Si definimos el costo como la log-verosimilitud negativa, entonces:
J(\theta) = - \sum_{i=1}^{N} \log P(\mathbf{y}_i | \mathbf{x}_i; \theta)
La capa de salida define la función de costo
Deep Learning Bayesiano
Podemos ver la red como un modelo paramétrico probabilístico
P(\mathbf{y}|\mathbf{x}; \theta)
Optimizar usando Máxima Verosimilitud
Si definimos el costo como la log-verosimilitud negativa, entonces:
J(\theta) = - \sum_{i=1}^{N} \log P(\mathbf{y} | \mathbf{x}; \theta)
J(\theta) = -\mathbb{E}_{\mathbf{x}, \mathbf{y} \sim \hat{p}_{data}} \log p_{model}(\mathbf{y} | \mathbf{x})
J(\theta) = - \sum_{i=1}^{N} \log p_{model}(\mathbf{y} | \mathbf{x})
Deep Learning Bayesiano
Podemos separar la capa de salida de las capas intermedias (features)
P(\mathbf{y}|\mathbf{x}; \theta) = P(\mathbf{y}|h(\mathbf{x}; \theta); W)
Salida capas ocultas
\(\mathbf{x}\)
\(h(\mathbf{x};\theta)\)
\(y(\mathbf{h};W)\)
Deep Learning Bayesiano
Tipo
Continua
Binaria
Discreta
Capa
Lineal
Sigmoidea
Softmax
Distribución
Gaussiana
Bernoulli
Categórica
Se puede definir con...
Asumiendo una...
Salida...
Deep Learning Bayesiano
Capa de salida Lineal
\hat{\mathbf{y}} = W^{\mathrm{T}}h(\mathbf{x})
Sirven para definir la media de una distribución Gaussiana
P(\mathbf{y}|\mathbf{x}) = \mathcal{N}(\mathbf{y}; \hat{\mathbf{y}}, I) \Rightarrow
Maximizar verosimilitud es minimizar MSE
Deep Learning Bayesiano
Capa de salida Sigmoidea
Se define para problemas de clasificación binaria (Bernoulli)
\hat{y} = \sigma(W^{\mathrm{T}}h(\mathbf{x})) = \sigma(z)
P(y|\mathbf{x}) = \frac{\exp(yz)}{\sum_{y'=0}^{1} \exp(y'z)} = \sigma((2y-1)z)
\Rightarrow -\log P(y|\mathbf{x}) = -\log \sigma((2y - 1)z) = \zeta((1 - 2y)z)
Notemos que la sigmoidea es buena no solamente por estar entre 0 y 1, también posee gradientes fuertes cuando la predicción es errónea
Deep Learning Bayesiano
Capa de salida Softmax
Se define para problemas multi-clase
\hat{y} = softmax(W^{\mathrm{T}}h(\mathbf{x})) = softmax(z)
softmax(z)_i = \frac{\exp(z_i)}{\sum_j \exp(z_j)}
\log softmax(z)_i = z_i - \log \sum_j \exp(z_j)
P(\mathbf{y}|\mathbf{x}) = Mu(\mathbf{y}|1,\hat{\mathbf{y}}) = \prod_{i=1}^{K} \hat{\mathbf{y}}_i^{\mathbb{I}(\mathbf{y}_i=1)}
Modelos Generativos
Modelos generativos que tienen interpretación probabilística
- Autoencoders Variacionales
- Encuentra representación latente donde \(p(z)\) es una distribución generadora de muestras, usualmente \(\mathcal{N}(0,1)\)
-
Generative Adversarial Networks (GANs)
- Entrenan dos redes
- Un generador \(G(z)\) que intenta replicar la distribución de los datos reales
- Un discriminador \(D(x)\) que determina si la entrada proviene de los datos reales o fue creada por el generador
- Las redes compiten hasta llegar a un equilibrio
- Entrenan dos redes
Programación Probabilística
Frameworks de Deep Learning han permitido desarrollar librerías de programación probabilística
- Edward
- GPflow
- Pyro
- ProbTorch
- PyMC3
Inferencia Variacional
Markov-Chain Monte-Carlo
Procesos Gaussianos
Modelos Bayesianos Jerárquicos
Modelos Lineales Generalizados
Referencias
Arquitecturas
- He et. al.; Mask R-CNN; International Conference on Computer Vision (ICCV); March 2017
- Liao et. al.; Visual Atribute Transfer through Deep Image Analogy; ACM Transactions on Graphics; July 2017
- Oord A. et. al.; WaveNet: A Generative Model for Raw Audio; arXiv pre-print; 2016
Métodos de Optimización
- Qian et. al.; On the Momentum Term in Gradient-Descent Algorithmns; Neural Networks; January 1999
- Duchi et. al.; Adaptive Subgradient Methods for Online Learning and Stochastic Optimization; Journal of Machine Learning Research; July 2011
- Zeiler M.; ADADELTA: An Adaptive Learning Rate Method; arXiv pre-print; 2012
- Kingma et. al.; Adam: A Method for Stochastic Optimization; International Conference on Learning Representations; 2015
Referencias
Otras referencias
-
Deep Learning Book,
Goodfellow I., Bengio Y., Courville A.,
MIT Press, 2016 -
Deep Learning Specialization,
Deeplearning.ai, - Introduction to Deep Learning,
MIT 6.S191, 2017
1 - Introducción a Deep Learning
By crsilva
