Notes on OT
History
- 1781, Monge - Initial approach
- 1942, Kantorovich - Modern Approach
- 1949, Dantzig - Solves problem numerically
- 1991, Brenier - Further math. advances
Measures
Discrete Measure
\alpha = \sum_{i=1}^{n} \mathbf{a}_i \delta_{x_i}
General Measure
\int_{\chi} f(x)\textrm{d}\alpha(x) = \sum_{i=1}^{n} \mathbf{a}_i f(x_i)
\int_{\mathbb{R}^d} h(x)\textrm{d}\alpha(x) = \int_{\mathbb{R}^d} h(x)\rho_{\alpha}\textrm{d}x
$$ \rho_{\alpha} = \frac{\textrm{d}\alpha}{\textrm{d}x} $$
Monge Problem
Given a Cost Matrix \( \mathbf{C}_{i,j}\) where \( i\in [[n]] \), \( j\in[[m]] \)
Assuming \( n = m \), the optimal assignment problem
seeks for a bijection \( \sigma \) in the set \( Perm(n) \) solving
$$ \min_{\sigma \in Perm(n)} \frac{1}{n} \sum_{i=1}^{n} \mathbf{C}_{i, \sigma(i)} $$
Monge Problem
$$ \min_{\sigma \in Perm(n)} \frac{1}{n} \sum_{i=1}^{n} \mathbf{C}_{i, \sigma(i)} $$
| 0 | 1 | 2 | 3 | 4 | 5 |
| 4 | 1 | 3 | 2 | 0 | 5 |
\( \sigma_1(i) \)
| 3 | 0 | 5 | 4 | 2 | 1 |
\( \sigma_2(i) \)
\( i \)
Find the best index combination between two measures such that cost is minimized
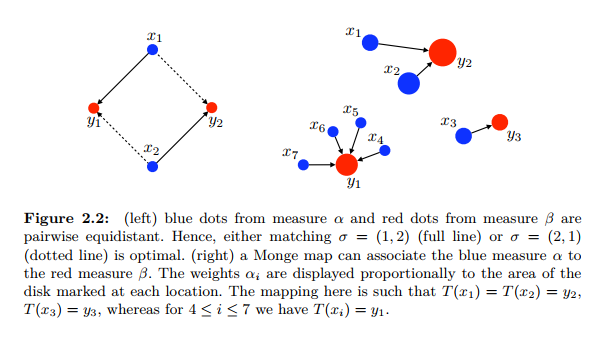
Monge Problem
OT
By crsilva
